古代历法气朔推算记录的复原
2018-05-14滕艳辉马俊青
滕艳辉,马俊青
(咸阳师范学院 数学与信息科学学院,陕西 咸阳 712000)
中国古代大量的历日和天象记录是现代地球科学、天文学和历史学重要的研究资料,而这些记录的可靠性问题就是非常值得研究的。因为有些记录不是真实的观测记录,可能是用当时历法推算的结果,也可能是故意捏造的天象,而即使是真实的观察记录,也存在观测精度的问题[1-2]。古代历日和天象记录的研究,一直是学者们长期关注的问题,他们在这方面取得了一系列成果[1-9]。然而,仍然有很多问题需要讨论和澄清,有很多史载的记录需要进一步考证。
史料中记载有用古代历法推算的天象结果。特别是在历法改革或评议中,经常出现由当时人陈述的历法推算的结果,用以说明某种历法推算的优劣。那么,这些实际陈述是不是准确的呢,需要我们重新对其进行验证。这个工作的第一步就是要根据当时的历法重新计算,复原史料中所描述的天象。然而这方面的工作量是巨大的,首先要确定天象发生的真实时间和所使用的历法,然后要理解当时历法的具体推算过程,并依照所用历法进行复原,最后比较复原结果与记录结果之间的差异。本文仅对《宋史》中记载的部分推算平气和定朔的记录进行分析。其他史料中的记录也可以使用本文的研究方法。
1宋代历法中的气朔算法
宋代历法中的气朔算法,已有很多相关研究[10-14]。本文为了计算和复原的方便,将气朔的计算公式综合起来,作为一套完整的数值算法系统进行展示。宋代历法求冬至及各气时刻的算法基本相同,若设A为日法,表示一日所包含的日分数,t=T/A为回归年常数,Nn是所求年(n年)到上元的积年数,则所求年冬至后第l个节气的具体时刻Tpq可由式(1)表示。

设u=U/A为朔望月常数,则所求年天正经朔后第k个朔的具体时刻Tpm(单位是日)由式(2)求得。
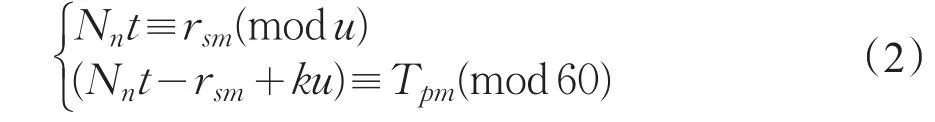
式中rsm表示冬至时刻与天正十一月经朔时刻的时间差,历法中一般称之为天正闰日及余。定朔的计算要复杂一些,是在经朔上加入太阳和月亮不均匀性的修正项,具体计算方法如公式(3)所示,计算结果单位是日。
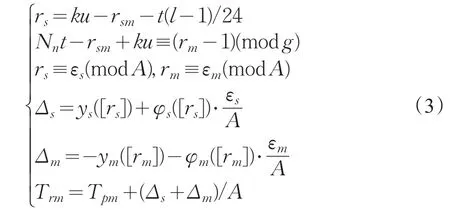
式中g=G/A是近点月常数;t 24表示一个气的长度,历法中一般称为气策;rs和rm分别表示所求经朔到最近一个气和最近一个近地点(或远地点)的时间(或距离),历法中一般称为入气日及余和入转日及余,它们不足一日的部分转换成日分数就是εs和εm;Δs和Δm即太阳和月亮的修正项;ys和ym分别是日躔表和月离表中的“朒胐积”(或“脁朒积”),φs和φm分别是日躔表和月离表中的“损益率”;k和l的意义与式(1)和(2)相同;Trm就是所求的定朔时刻。需要说明的是,ym和φm可以直接根据rm的整数值查找相应日数的数据,而ys和φs则根据历法中所给的每气的日躔数据通过插值算法计算得到每一气每一天的数值,然后用l确定查哪气的表,用rs的整数值查找相应日数的日躔数据。关于每一天日躔数据的计算,可参考文献[12]。
2《宋史》中的气朔推算记录
宋史中的天象记录很多,但明确记载使用当时历法进行推算且有详细推算结果的记录相对较少。《宋史》中记载使用历法推算气朔的记录,目前仅发现6处。我们对这6条记录进行重新计算,复原当时历法推算的情况。
这些记录中,有些明确给出使用哪部历法进行计算,个别则没有明确说明。特别是在改历前后,进行验历的过程中,那当时用以推算的历法不好确定。对此,在必要时我们选择改历前后可能使用推算的几部历法同时进行复原推算。为了更清楚各部历法的基本天文常数,方便计算过程中随时使用,我们将这6条记录可能涉及的历法的基本信息和常数列于表1中。
2.1节气推算记录的复原
《宋史》记载历法推算节气的记录有两条。第一条是:“今年十一月冬至,日景表当在十九日壬午,《会元历》注乃在二十日癸未,系差一日。《崇天历》癸未日冬至加时在酉初[二刻]七十六分,《纪元历》在丑初一刻六十七分,《统元历》在丑初二刻二分,《会元历》在丑初一刻三百四十分。”[15]2890

表1宋代历法基本常数
在讨论《会元历》推算绍熙四年(1193)冬至时刻的精度时,历家利用历法推算结果与实测结果相比较。实测冬至应该在十一月十九壬午日,而四部历法都推算得癸未日。历法推算绍熙四年的冬至实际上使用1194年的数据,即公式(1)中n=1 194。以下计算中的积年选取方式与此同。N1194的计算方法是用历法的上元积年加上历法行用年份与1194年的差值。例如,《崇天历》的计算方法是十一年历,称成永祥等依《开禧》新历推算,辛亥岁十二月[二]十七日立春在酉正一刻,今所颁历乃相师尧等依《淳祐新历》推算,到壬子岁立春日在申正三刻。”[15]2896

这是在用《开禧历》和《淳祐历》推算1252年的立春气时刻。由于《淳祐历》已经失传,我们仅能使用《开禧历》进行复原。《开禧历》上元到1152年积年为N1252=N1208+(1252-1208)=7848184+44=7848228,由于立春为冬至后第3气,则l=3,代入公
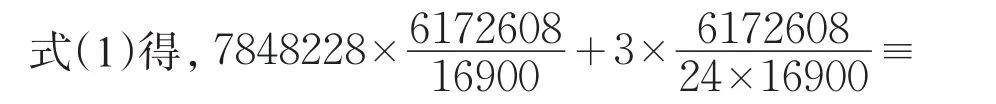
其他历法与此类似。可得《纪元历》的N1194=28 613 554,《统元历》的 N1194=94 251 650,《会元历》的N1194=25 494 770。

癸未日丑初一刻340.5分。需要说明的是,我们复原的结果在由日分转换为辰刻时,日法除以12得到一辰的日分数,日法除以100得到一刻的日分数。每一日以子正起算,每辰由初刻、一刻、二刻顺序计算,即每辰时刻为初刻。下面其他记录复原时,计算方式与此同。
通过比较,我们发现史载的记录是我们复原结果取整后的数值,可以说,我们的复原与史料相合。而通过现代计算得,1193年冬至时刻在12月14日(壬午)14时49分[16]。
第二条节气推算记录是:“今淳祐十年冬所颁正一刻325分,与史载记录相合。而现代计算的结果是1152年立春在1月28日(癸卯)7时13分[16]。
2.2定朔推算记录的复原
《宋史》记载历法推算定朔的记录有四条。



朒积ys(2)=54.1①《纪元历》的日躔数据采用文献[12]已经复原的结果,其余历法的日躔数据系作者根据历法进行插值计算的结果。。由此得入气腓朒定数
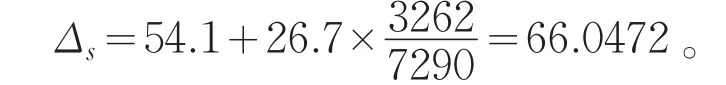

《纪元历》入转日求法是得到绍兴四年十二月定朔为乙亥日5 466.596 2日分,日分除以日法7 290乘以10 000得7 499。按照《纪元历》月份安排规则,在秋分后定朔小余超过四分之三日才要进朔,而我们复原的结果不足7 500,因此太史不进朔是正确的。本次复原过程中必要的变量结果列于表2中。
使用《崇天历》和《统元历》推算本次定朔的过程与上面过程类似,我们不再重复写出这些计算过程,仅是将公式(2)和(3)中的中间变量的计算结果和最终复原结果列于表2中。后面几条记录的推算,我们也不再重复写出推算过程,仅将计算结果列出在表2中。要说明的是,《崇天历》入转日从远地点起算,与其余历法不一样;入转胐朒定数计算时如果入转日是七日、十四日、二十一日和二十八日时,算法会略有不同,具体算法参考文献[12]。复原的结果是,《崇天历》和《统元历》定朔日分8 111.575 4和5 315.058 3分别除以各自日法乘以10 000得7 660和7 670,那么,按照这两部历法推得的定朔确实要进朔的,而且数值与史载的7 680也更接近些。
第二条记录是接着第一条的,陈得一继续指出:“今年(绍兴五年)五月小余七千一百八十,少三百二十,乃为进朔,四月大尽。”[15]2869他认为用历法推算绍兴五年五月定朔小余为7 180,结果太史进朔了,这是不应该的。因绍兴五年闰二月,五月相当于天正经朔后第7个朔。计算结果表明,《纪元历》定朔5 367.466 0日分,合小余7 363,《崇天历》定朔7 736.919 3日分,合小余7 306,《统元历》定朔5 028.635 5日分,合小余7 256。三历结果都不是7 180,但确实小余都不到7 500,至于其中的原因,还有待于更深入的讨论。

表2各部历法计算定朔时刻的过程和结果
第三条记录是:“乾道二年,日官以《纪元历》推三年丁亥岁十一月甲子朔,将颁行,裴伯寿诣礼部陈《统元历》法当进作乙丑朔,于是依《统元历》法正之。”[15]2870当时行用《统元历》,但是历官经常使用《纪元历》推算,推算乾道三年十一月的朔(1167年12月13日),裴伯寿认为不当。我们复原的结果表明,历法推的定朔日都在甲子日,《纪元历》定朔5 461.743 3日分,合小余7 492,此朔不进;《统元历》定朔5 218.094 1日分,合小余7 530,此朔当进。由此看来,裴伯寿所说的与我们复原的一致,符合事实。
最后一条记录是:“乾道十年颁赐历日,其中十二月已定作小尽,乾道十一年正月一日注:癸未朔,毕乾道十一年正月一日。《崇天》、《统元》二历算得甲申朔,《纪元》、《乾道》二历算得癸未朔,今《乾道历》正朔小余,约得不及进限四十二分,是为疑朔。”[15]2882乾道十一年(1175)正月朔,四部历法推算结果不尽相同,当时行用的《乾道历》推算失误,不当进朔而进朔。我们复原的结果是,四历定朔都在癸未日,《乾道历》定朔22 371.077 0日分,合小余7 457,《崇天历》定朔7 884.689 0日分,合小余7 445,《统元历》定朔5 111.969 5日分,合小余73 77,《纪元历》定朔5 397.484 3日分,合小余7 401。四历结果都达不到进限,乾道历小余不及进限43分,与史载相吻合①《乾道历》定朔小余7 457后面还有小数部分,减7 500,实际结果不足43,按照古代历法计算经常取整的做法,可得不及进限应该是42分。。
3结语
我们完全按照历法的计算过程复原了《宋史》中六条气朔记录。我们完整地给出两条平气推算记录和一条定朔推算记录的复原计算过程,由于篇幅所限,其余的计算只给出了推算中涉及的中间变量的数值和复原的结果。对于史料中出现的其他关于气朔的记录,我们可以按照给出的公式和复原的算例进行复原计算,同时,关于宋代朔闰考证,本文的公式和计算过程,也具有一定的参考价值。
两条节气记录的史载结果与复原结果一致,这不但能够证明史料记载的正确性,也可间接说明我们对历法理解是正确的。而对于4条定朔记录,其中两条与复原结果一致,另两条记录与复原结果有一定差距,但不明显。绍兴四年十二月的记录,使用《纪元历》推算应该不进朔,而使用《统元》和《崇天》则都要进朔,记录中没有明确使用了哪部历法,因此,我们推测陈得一可能使用《统元历》进行推算,与太史所用历法不同。绍兴五年五月的记录,三部历法推算的定朔小余都在7 500以下,结果都应该不进朔。复原结果与史载的7 180不合。这可能与我们复原计算中运算的顺序及小数的取舍与当时历家的操作不同有关,也可能另有其他原因,至于真相是什么,将是我们下一步认真研究的问题。
参考文献:
[1]黄一农.星占、事实与伪造天象——以“荧惑守心”为例[J].自然科学史研究,1991,10(2):120-132.
[2]薄树人.古代日食观测模拟实验报告[M]//薄树人文集.合肥:中国科学技术大学出版社,2003:320-325.
[3]邢钢,石云里.汉代日食记录的可靠性分析——兼用日食对汉代历法的精度进行校验[J].中国科技史杂志,2005,26(2):107-121.
[4]李勇.两汉《五行志》中的日食记录研究[J].天文学报,2015,56(5):491-505.
[5]刘次沅.二十五史天象记录校勘举隅[J].文史,2014(1):123-136.
[6]刘次沅,窦忠,庄威风.明代大食分日食记录考证[J].陕西天文台台刊,1998(1):84-98.
[7]LIU CY.The regular records of solar eclipse in ancient China and a computer readable table[J].Achieve for History of Exact Science,2005,59(2):157-168.
[8]张培瑜.中国古代月食记录的证认和精度研究[J].天文学报,1993(1):63-79.
[9]黄一农.中国史历表朔闰正举隅——以唐《麟德历》行用时期为例[J].汉学研究,1992,10(2):305-332.
[10]刘金沂,赵澄秋.《麟德历》定朔计算法[M]//薄树人,刘金沂.中国天文学史文集:第3集.北京:科学出版社,1984:36-88.
[11]李勇,张培瑜.中国古历定朔推步综述[J].天文学进展,1996,14(1):66-76.
[12]薄树人.《纪元历》解[M]//薄树人文集.合肥:中国科学技术大学出版社,2003:369-405.
[13]滕艳辉,王鹏云.《纪元历》等8部宋代历法的定朔推步及精度分析[J].中国科技史杂志,2009,30(1):55-64.
[14]滕艳辉,王鹏云.《纪元历》定朔算法模型及分析[J].西北大学学报(自然科学版),2008,38(5):855-858.
[15]脱脱,帖睦尔达世,贺惟一,等.宋史·律历志[M]//中华书局编辑部.历代天文律历等志汇编:第8册.北京:中华书局,1976.
[16]张培瑜.三千五百年历日天象[M].郑州:河南教育出版社,1990:940-941.
[17]滕艳辉.宋代朔闰与交食研究[D].西安:西北大学,2012:144-145.
