分析数与数之间的关系
2018-05-14◎李英
◎李 英
分析数与数之间的变化规律,需要我们认真分析题目中所给的数据与未知数据的联系,从中发现规律,按规律填数,从而解决问题。
例1:观察分析下面各列数的变化规律,然后进行填空。
(1)3、6、9、12、( )、18、21
(2)1、3、9、27、( )、243
(3)28、26、24、22、( )18、16
(4)1、4、9、16、( )、36、49
思路点睛:分析一列数的变化规律,一般是对这列数中相邻的几个数依次进行相同的四则运算,根据计算结果进行比较,从中找到规律。
比如(1),后一个数依次比前一个数多3,于是得到括号中缺少的数是15;(2)中,后一个数依次是前一个数的3倍,于是得到括号中缺少的数是81;(3)则是后一个数依次比前一个数少2,都是双数,很显然,括号内要填20;(4)要稍难一些,因为不论是加还是减,都不易看出规律,此时需要我们把它们写下来看:
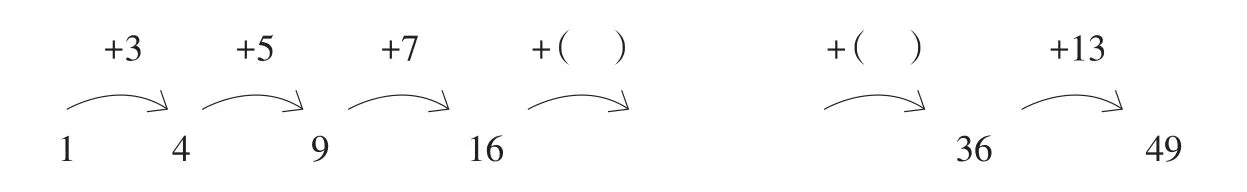
哦,原来后一个数依次比前一个数多3,多5,多7,多9,多11,多13!括号内是25。
例2:观察下面各列数的变化规律,然后进行填空。
(1)1、1、2、3、5、8、13、21、( )、( )
(2)1、2、2、4、8、32、( )、( )
思路点睛:表面上看这些数列规律不明显。这是因为我们的眼光仅仅局限于“相邻的两个数”之间,仅对这两个数依次进行计算、比较结果。如果我们能放开眼光,看完整个数列,也许解答就简单了!
(1)从第三个数开始,后一个数依次是前两个数的和,括号里填34,55;(2)从第三个数开始,后一个数依次是前两个数的积,填出256,8192。
对于比较简单的数列,一般由相邻两数的和、差、积、商找排列规律,或者把数列拆成几个部分,分别考察它们的排列规律。在填数时,一要细心观察题目中数字特点;二要灵活运用整数的有关知识和加、减、乘、除的计算法则,以及它们之间的关系进行合理的推想。
请你也来练一练:观察下列各组数的排列规律,然后填空。
(1)5、9、13、17、21、( )、( )
(2)5、7、11、17、25、( )、( )
(3)2、2、4、6、10、16、26、( )、( )
