基于智能磁性石块埋入的边坡深部变形失稳监测模型

江胜华，刘晓春，孙伟贺，宋韫皓，胡 嫚 ，汪时机

（1. 西南大学工程技术学院，重庆 400715；2. 南洋理工大学土木与环境工程学院，新加坡 639798；3. 中南大学土木工程学院，长沙 410075）

0 引 言

边坡变形破坏是一个渐变到突变的累积发展过程，滑动失稳由深部变形逐渐扩展演化至表面形成滑动面的结果[1-3]，但边坡临近失稳破坏时呈现突变性和随机性[4-5]，因此，边坡深部变形失稳监测尤为重要。现有的边坡深部变形失稳监测方法主要有钻孔测斜仪、滑动测微计、多点位移计、CT物探、声波、地震波、电磁波时域反射（Time domain reflectometry，TDR）[6-7]、光纤光栅[8]等。其中，钻孔测斜仪、滑动测微计、多点位移计等存在测杆、电缆等仪器布设较繁琐的缺点，而TDR监测技术仅可确定滑动面的位置，无法确定边坡滑动的方向，更无法测量边坡的变形量，且设备造价高昂；CT物探、声波和地震波同样存在无法精确测量边坡变形量的缺点，光纤光栅测量技术需要结合测斜管，存在布设困难等缺点。另一方面，现有监测方法易受雨水、滚石、泥石流等环境破环，难以在野外恶劣环境下服役，需要人工定期巡检和精心维护。因此，有必要研制在恶劣环境下服役性能可靠且布设简便的边坡深部变形监测方法及其支撑设备，是解决边坡变形失稳预测的主要方法和技术之一，在边坡深部变形较大的特征点或者滑动面附近布置传感器，对边坡变形失稳进行预警，为边坡工程在全寿命服役过程中提供安全保障。

磁测技术具有稳定、可靠、抗干扰等特点[9]，且磁测技术中极低频或静场磁信号可穿透岩石、土体、水流[10-13]，在恶劣服役环境下具有生存率高、布设简便、维护工作量小、可监测边坡深部大变形的优点，是一项值得深入研究的监测技术。针对边坡深部变形失稳的时空特征，构建基于智能磁性石块的边坡变形监测系统，提出磁场梯度张量缩并的简化算法，实现基于磁场梯度张量定位的边坡深部变形失稳监测方法；研制便捷且低成本的全张量磁场梯度传感器和智能磁性石块，设计推移式边坡物理模型试验，通过与传统的变形监测结果进行比较验证智能磁性石块的监测性能。

1 基于智能磁性石块的边坡变形监测方法

基于智能磁性石块的边坡深部变形失稳监测系统包括智能磁性石块和全张量磁场梯度传感器。将磁性标签封装在环氧工程塑料（或轻质混凝土）中，即智能磁性石块。在边坡深部钻孔布置智能磁性石块，在边坡表面选择若干稳定的位置作为参考点处布置全张量磁场梯度传感器。智能磁性石块随着边坡变形而移动时，其激发的磁场会相应发生改变，则全张量磁场梯度传感器测量到磁场后，通过磁场反演智能磁性石块的三维位置，根据智能磁性石块的位移变化判断边坡的变形演化及稳定安全。

智能磁性石块由磁性标签、封装层和轻质混凝土外壳组成，见图1。磁性标签由用钕铁硼永磁铁和万向支架组成[7]，采用抗冲击、耐低温、耐高温且阻燃的 ABS工程塑料封装，再浇筑成轻质混凝土块。全张量磁场梯度传感器包括4个三轴磁场传感模块（美国PNI公司生产，型号为MicroMag3）和STC90C516RD芯片处理器（深州宏晶科技有限公司生产），4个三轴磁场传感模块的空间布置见图2。式中 m为磁矩， m = mx2+ m2y+ mz2，mx=msinθcosφ，my=msinθsinφ，mz=mcosθ，A·m2，其中，（θ，φ）为方位角，(°)，θ 为磁偶极子的轴线与 z轴的夹角，φ 为磁偶极子的轴线在xoy平面的投影与x轴的夹角。r为智能磁性石块至参考点的距离，k为参数。

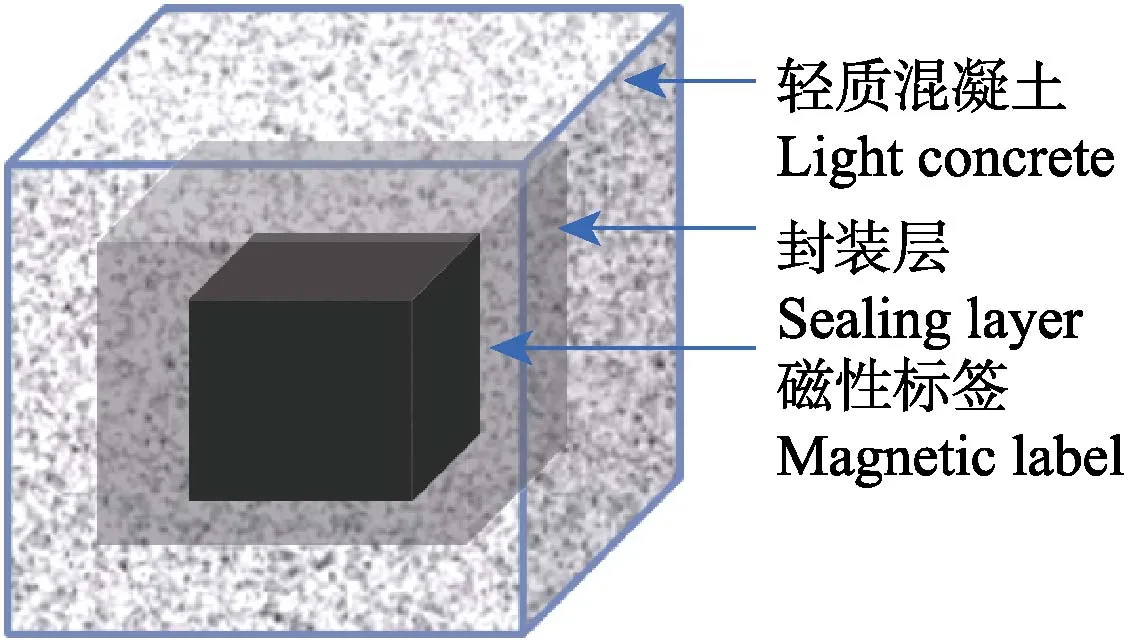
图1 智能磁性石块的结构Fig.1 Structure of smart magnetic rock

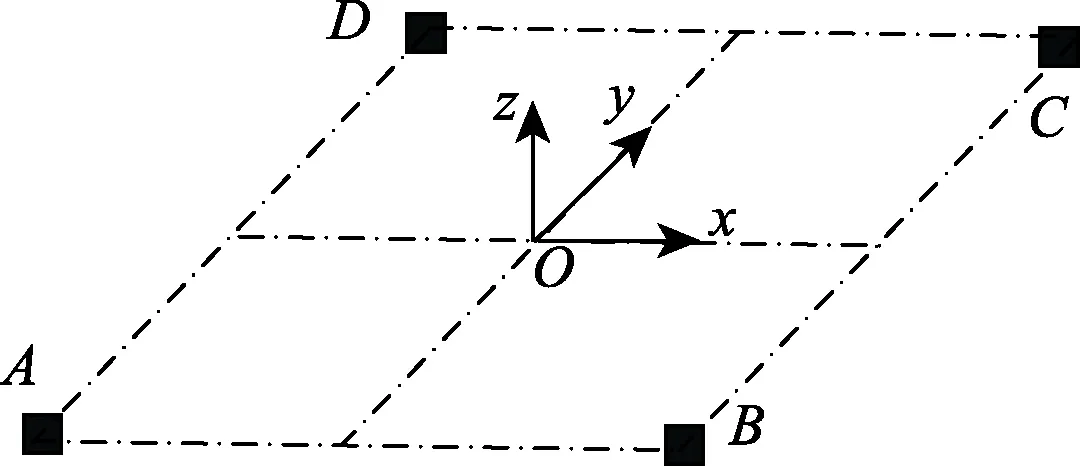
图2 全张量磁场梯度传感器的结构Fig.2 Structure of full tensor magnetic gradient sensor

k与智能磁性石块至参考点的距离r无关，取决于智能磁性石块至参考点的连线和磁偶极子的轴线的夹角。式（6）中，参数k近似为[17-18]

当智能磁性石块中的磁性体（钕铁硼永磁铁）至测点（参考点）的距离超过磁性体长度的25倍时，可将磁性体（磁性标签中的钕铁硼永磁铁）视为一个磁偶极子模型[14]，则智能磁性石块在参考点处的磁感应强度为

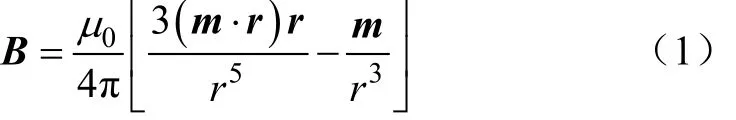
式中μ0为介质磁导率，m(mx, my, mz)为智能磁性石块的磁矩，在边坡钻孔布设智能磁性石块前测定其磁矩，r为智能磁性石块至参考点的位矢，r=r，m。

智能磁性石块在参考点处的磁场梯度张量[15]为

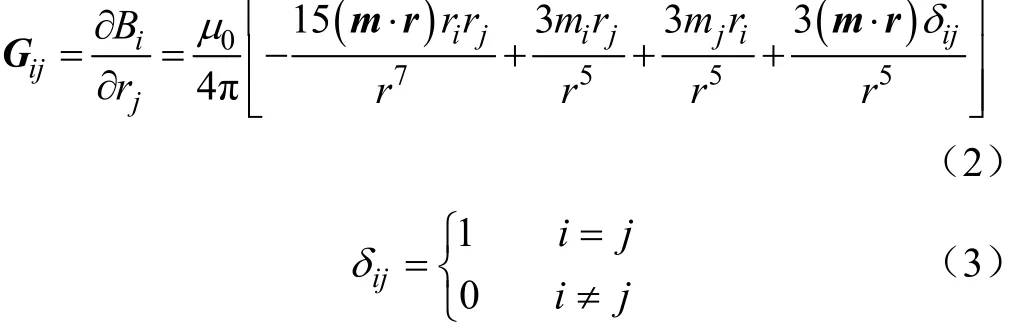
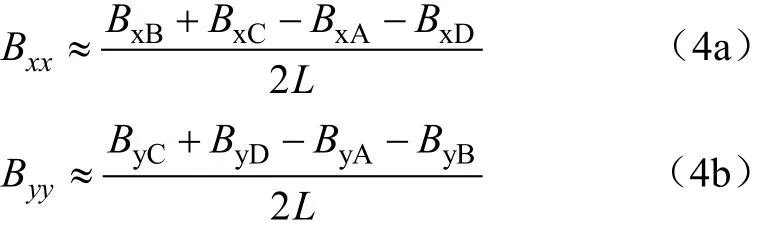
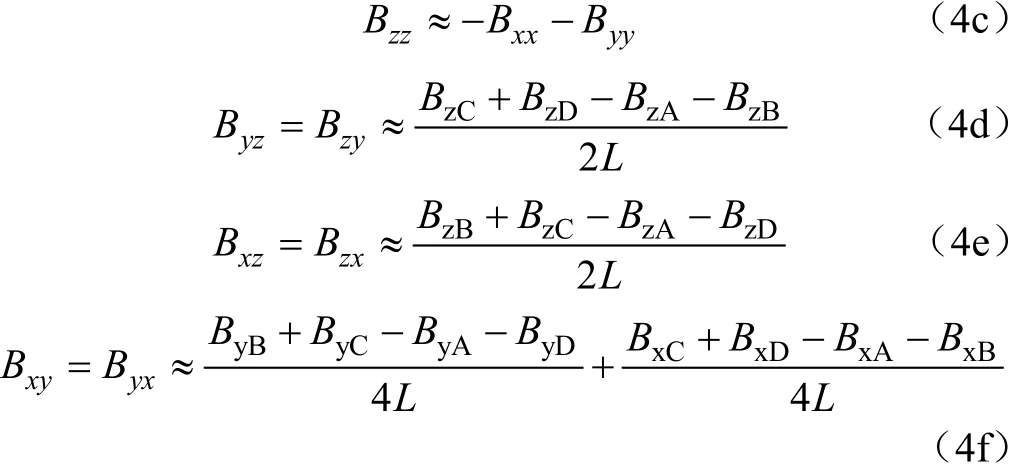
在实际监测时，智能磁性石块在参考点处的磁场梯度张量由全张量磁场梯度传感器测量得到式中Bxi、Byi和Bzi（i=A、B、C、D）为4个三轴磁传感模块的磁感应强度，nT，L为三轴磁传感模块之间的基线距离，m。

智能磁性石块在参考点处的磁场梯度张量的模量为式中Gij为磁场梯度张量，由全张量磁场梯度传感器测量得到。

智能磁性石块至参考点的距离可表示为[16]

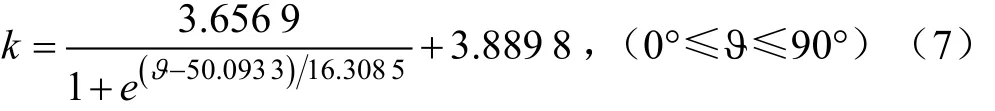
式中ϑ为智能磁性石块至参考点的连线与磁偶极子的轴线的夹角。当 90°≤ϑ≤180°时，参数 k的取值与 0°≤ϑ≤90°对应的取值对称。

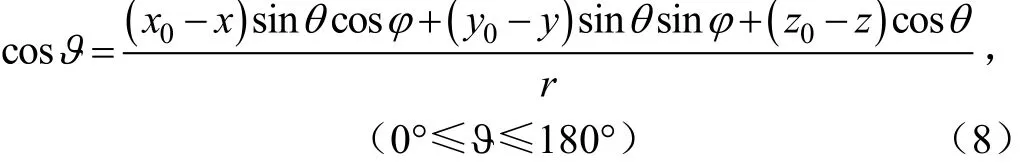
式中(x, y, z)为智能磁性石块的坐标，(x0, y0, z0)为参考点的坐标。

对于智能磁性石块，钕铁硼永磁铁置于万向支架的中心，钕铁硼永磁铁的磁偶极子的轴向始终保持竖直，即θ=0[13,18]，磁矩参数m(mx, my, mz)可简化为m(0,0, m)[13]，同时式（8）简化为

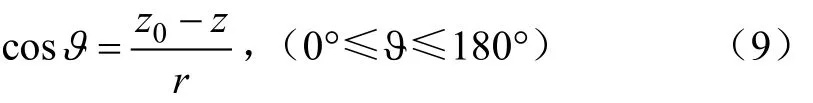
由于边坡变形过程中，智能磁性石块的位移变化远小于智能磁性石块与各参考点之间的距离，即Δx ≪x0-x ， Δy ≪y0-y ， Δz ≪z0-z ，则边坡变形过程中，各参考点处近似认为ϑ恒定，即各参考点处k恒定。

在埋设智能磁性石块时，选择至少3个参考点(xi, yi,zi)，（i=1，…，n，n≥3），先测量智能磁性石块的初始三维位置和参考点的三维位置。采用全张量磁场梯度传感器测量时，全张量磁场梯度传感器的z轴方向必须竖直向上，与智能磁性石块的磁偶极子的轴线方向一致，x轴和y轴方向可自行定义。在各参考点处根据全张量磁场梯度传感器的测量数据，由式（4）～（7）计算各参考点处的ki；同时亦根据式（7）～（9）计算ki进行验证。

在边坡变形过程中，由全张量磁场梯度传感器在各参考点测量得到智能磁性石块的磁场梯度张量Gij，由式（4）～（6）和前述的ki计算智能磁性石块至各参考点的距离为ri，则

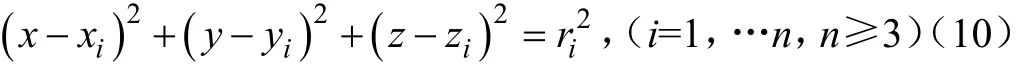
由式（10）计算智能磁性石块任意时刻的三维位置，与智能磁性石块初始状态的三维坐标比较，得到智能磁性石块的三维位移变化(Δx, Δy, Δz)，可进一步评价边坡的深部变形稳定状态。

2 模型试验

现有的边坡模型试验大致有降雨加载[19-20]、顶部竖向加载[21]、离心加载[22]、倾斜加载[23-25]、推力加载[26-27]等。针对推移式滑坡及堆载引起的滑坡[28-29]，均可近似为推力引起的边坡滑动失稳，同时考虑到推力对边坡滑动的作用[30]，本文采用推力加载方式的模型试验。在模型槽中制作土质边坡模型，采用边坡后端的推移加载装置使边坡逐渐滑移发生失稳破坏，研究智能磁性石块在边坡深部变形失稳过程中的变形监测性能。模型槽尺寸为2 m×1 m×1 m（长×宽×高），模型槽采用铝合金型材、铝合金螺栓及有机玻璃制作，通过分离式千斤顶和力传感器在边坡后端施加推力模拟土体的推力或堆载引起的侧压力。在推移边坡时为减小土体和有机玻璃之间的摩擦阻力，在底面和侧面的有机玻璃上涂抹 3号钙基润滑脂。为验证和比较智能磁性石块的边坡变形监测情况，选择 6个特征点并设置相应的标识，坡面和坡顶面各 3个；在模型槽的有机玻璃上粘贴10道水平方向的菲林软尺和5道竖直方向的菲林软尺（测量精度为0.5 mm，实际测量时估读到0.1 mm），采用菲林软尺测量6个特征点的位移。智能磁性石块中磁性标签为钕铁硼永磁铁，剩磁为1.23 T，矫顽力为860 kA/m，磁矩约0.373 A·m2。本文模型试验中，仅埋设了 1个智能磁性石块，如埋设多个智能磁性石块，尚需要考虑不同智能磁性石块之间的影响。以智能磁性石块埋设的初始位置为原点，z轴方向竖直向上，x轴方向沿模型槽长度方向，y轴方向沿模型槽宽度方向。在模型槽上选择 3个参考点，坐标分别为 P1(0.136, 0.023, 0.825)、P2(0.407, -0.378, 0.825)和P3(0.407, 0.342, 0.825)，设边坡变形过程智能磁性石块的坐标为P0(x, y, z)。试验选用嘉陵江重庆北碚段正码头附近天然河砂，其干密度为1 590 kg/m3，含水率为10.2%，内摩擦角为43.2°，孔隙比为0.76%。模型边坡高为0.4 m，坡肩至推移板的距离为 0.4 m，坡趾至推移板的距离为1.25 m。边坡模型示意图和实物图见图3，智能磁性石块和全张量磁场梯度传感器的实物图见图4。

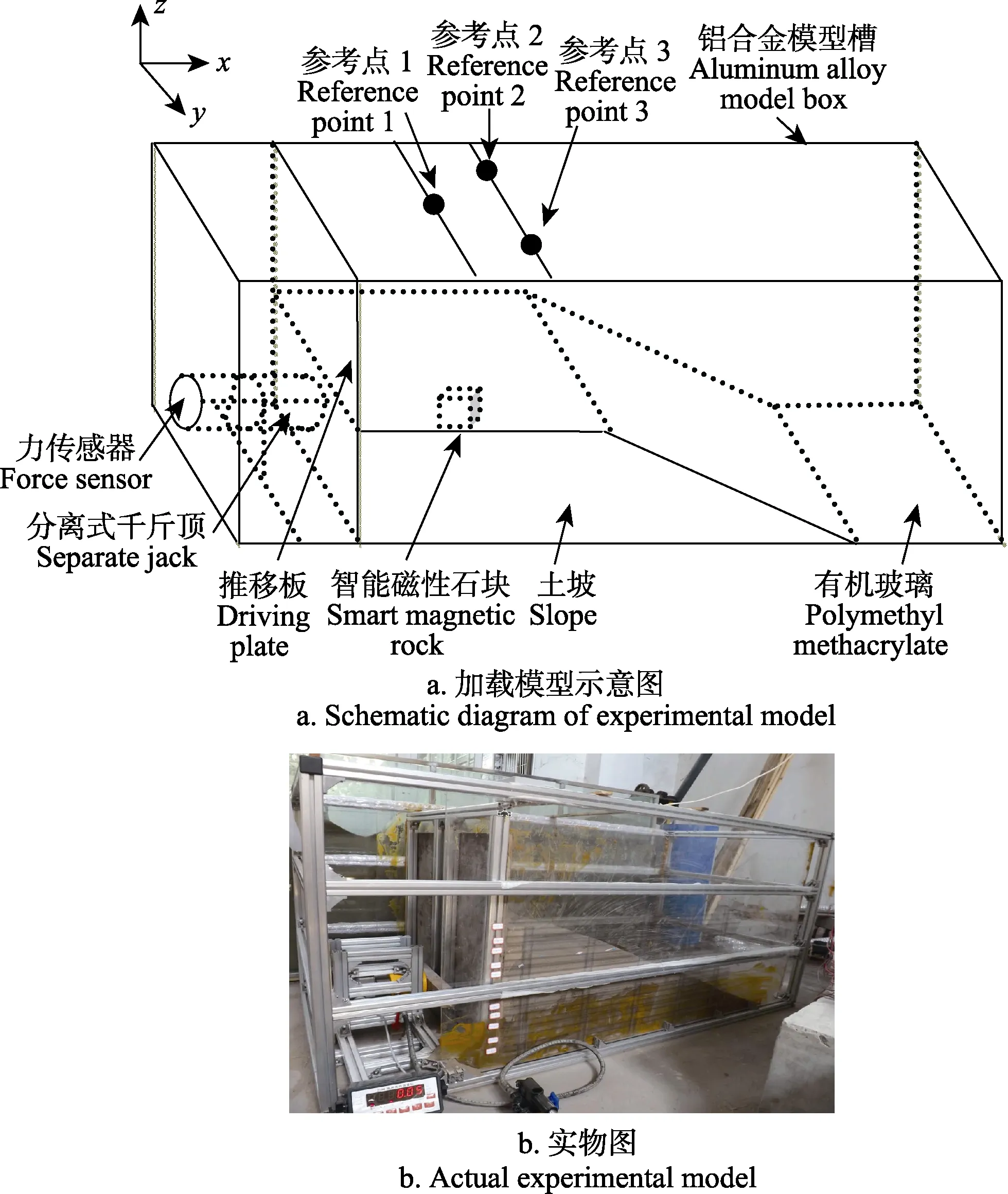
图3 边坡模型试验示意图Fig.3 Sketch of slope model loading

图4 智能磁性石块和全张量磁场梯度传感器的实物图Fig.4 Sketch of smart magnetic rock and full tensor magnetic gradient sensor

加载系统采用推移方式模拟土体侧压力，采用液压分离式千斤顶施加推移荷载，分17级荷载加载至3 200 N，每级荷载维持15 min，采用力传感器测量液压分离式千斤顶的推力，测量精度为10 N。在边坡表面6个特征点通过菲林软尺测得的水平位移与推力的关系见图5。通过式（1）～（10），采用全张量磁场传感器测量 3个参考点至智能磁性石块的相对距离，然后得到智能磁性石块的位移。在本试验中，智能磁性石块未发生翻滚而接近水平移动，故仅给出智能磁性石块的水平位移。由于全张量磁场传感器的精度有限和本文中算法的误差，在本试验中，仅在推力大于1 000 N时方可测得有效数据。由于智能磁性石块至 3个参考点的相对距离与推力的变化关系基本一致，仅给出智能磁性石块至各参考点P2的相对距离与推力的关系，见图6；智能磁性石块的水平位移与推力的关系见图6。

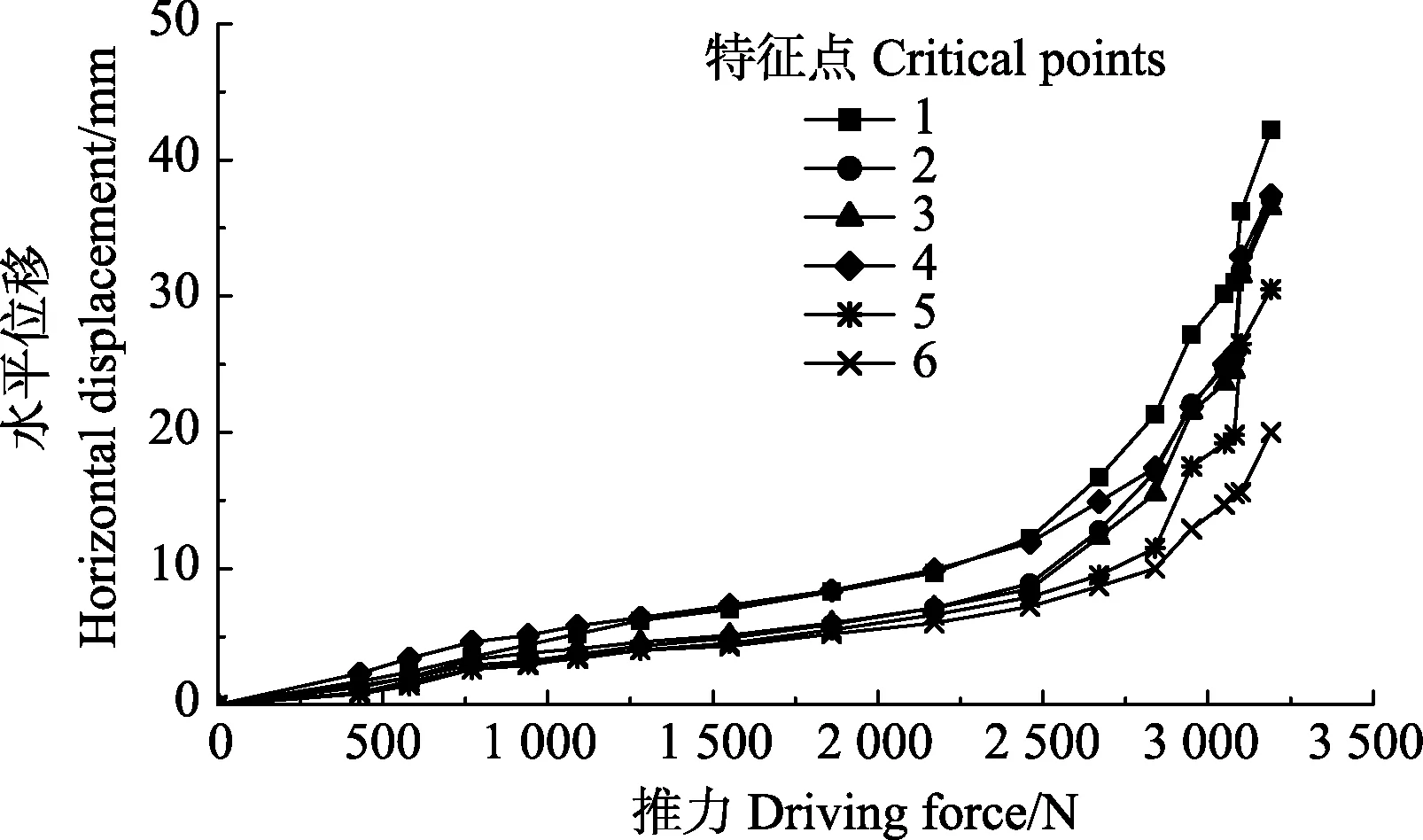
图5 边坡特征点水平位移与推力的关系Fig.5 Relationship between critical points’ horizontal displacement and driving force

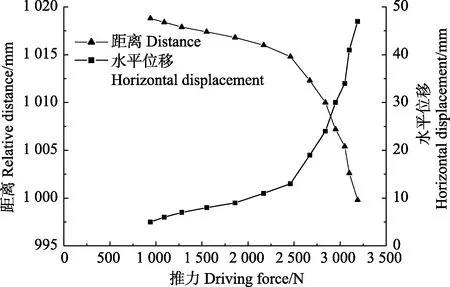
图6 智能磁性石块至参考点（P2）的距离、智能磁性石块的水平位移与推力的关系Fig.6 Relationship between relative distance from smart magnetic rock to reference point (P2), horizontal displacement and driving force

由图5可得，当推力＜2 500 N时，通过菲林软尺测得的 6个特征点的水平位移与推力之间的曲线关系接近于线性关系；当推力为2 500 N左右时，水平位移与推力的曲线关系存在拐点和突变，此时边坡处于临界稳定状态；当推力在2 500至3 100 N时，随着推力增加水平位移迅速增大，分离式千斤顶的行程大幅度增加而力传感器显示的荷载增加幅度很小，最后力传感器的推力稳定在3 100 N左右，此阶段为边坡发生失稳破坏的滑动阶段。因此，由边坡表面的 6个特征点水平位移可判断，在推力为2 500 N时，边坡为临界稳定状态，之后发生失稳破坏。

由图6可得，当推力＜2 500 N时，智能磁性石块至参考点的距离与推力的关系近似为线性关系；当推力为2 500 N左右时，智能磁性石块至参考点的距离与推力的曲线关系存在拐点和突变；当推力在2 500至3 000 N时，随着推力增加智能磁性石块至参考点的距离迅速减小。

由图6可得，当推力为2 500 N时，智能磁性石块的水平位移与推力的曲线发生突变，曲线存在明显的拐点。可见，通过智能磁性石块至参考点的距离、智能磁性石块的位移等可判断在推力为2 500 N时边坡为临界稳定状态，之后发生失稳破坏，其结果与菲林软尺的位移监测结果的趋势基本一致。

3 结 论

1）针对边坡深部变形监测存在服役环境恶劣、传感器布设困难等问题，提出了基于智能磁性石块的边坡变形监测方法，研制了智能磁性石块及全张量磁场梯度传感器，提出了基于智能磁性石块的边坡变形监测的简化算法。

2）采用铝合金模型槽、分离式千斤顶和力传感器建立了滑坡模拟系统，通过推移加载方法模拟边坡滑动，结合全张量磁场梯度传感器和智能磁性石块，采用边坡模型试验验证了基于智能磁性石块的边坡深部变形失稳监测方法。

3）采用菲林软尺测得的结果表明，当推力为2 500 N时，6个特征点的水平位移与推力的曲线关系发生突变，当推力在2 500至3 100 N时，6个特征点的水平位移增加幅度迅速提高，发生失稳破坏。采用智能磁性石块测得的结果表明，当推力为2 500 N时，智能磁性石块至参考点的距离、智能磁性石块的水平位移与推力的曲线关系存在拐点，此后智能磁性石块至参考点的距离大幅度减小、智能磁性石块的水平位移大幅度增大，两者均大幅度发生变化。智能磁性石块至参考点的相对距离、智能磁性石块的位移等均可反映边坡变形演化和失稳评价，且与菲林软尺传统的监测结果的趋势基本一致。

由于边坡深部变形监测具有重要的物理意义和工程意义，且基于磁场的位移监测方法可穿透岩石、土体、淤泥和水流等，考虑多个智能磁性石块干扰情况下基于智能磁性石块网络的边坡深部变形监测值得进一步的研究。

[参 考 文 献]

[1] 邓建华. 地表变形测量技术在滑坡稳定性监测中的应用研究与实例分析[D]. 成都：成都理工大学，2011 Deng Jianhua. Research and Case Study in Measurement of Surface Deformation Monitoring in Landslid[D]. Chengdu:Chengdu University of Technology, 2011. (in Chinese with English abstract)

[2] 陈新建. 基于破损力学的黄土滑坡机理研究[D]. 西安：长安大学，2013 Chen Xinjian. Study on the Mechanicals of Loess Landslide Based on Breakage Mechanics[D]. Xi’an: Chang’an University, 2013 (in Chinese with English abstract)

[3] 唐晓松，郑颖人，唐辉明. 边坡变形破坏演化特征的数值分析[J]. 重庆大学学报: 自然科学版，2013，36(10)：101－113 Tang Xiaosong, Zheng Yinren, Tang Huiming. Numerical analysis on the evolutionary features of deformation and failure modes of slopes[J]. Journal of Chongqing University,2013, 36(10): 101－113 (in Chinese with English abstract)

[4] Duncan J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 307－316.

[5] Bea R. Reliability and human factors in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 631－643.

[6] Anderson Neil, Welch David. Practical applications of time domain reflectometry (TDR) to monitor and analyze soil and rock slopes[C]// Geo-Denver. 2000: 65－79.

[7] Serafini David C, Fiegel Gregg L. Estimating slope movement with time domain reflectometry (TDR)[C]//Geotechnical Engineering for Transportation Projects. ASCE,2004: 2084－2092.

[8] 邢厚俊. 光纤光栅传感技术用于铁路边坡滑动监测的试验研究[J]. 铁道建筑，2018，58(2)：85－88 Xing Houjun. Experimental study on railway slope sliding monitoring with optical fiber grating sensing technology[J].Railway Engineering, 2018, 58(2): 85－88 (in Chinese with English abstract)

[9] Marechal L, Foong S, Ding S Y, etal. Optimal spatial design of non-invasive magnetic field-based localization systems[C]// 2014 IEEE International Conference on Robotics and Automation. Hong Kong, 2014: 3510－3516.

[10] 江胜华，周智，欧进萍. 基于磁场梯度定位的边坡变形监测原理[J]. 岩土工程学报，2012，34(10)：1944－1949.Jiang Shenghua, Zhou Zhi, Ou Jinping. Slope deformation monitoring principle based on magnetic gradient tensor[J].Chinese Journal of Geotechnical Engineering, 2012, 34 (10):1944－1949 (in Chinese with English abstract)

[11] 江胜华，周智，欧进萍. 基于磁测的边坡深部大变形监测方法[J]. 岩土力学，2013，34(10)：3033－3038.Jiang Shenghua, Zhou Zhi, Ou Jinping. Slope internal large deformation monitoring using magnetic survey[J]. Rock and Soil Mechanics, 2013, 34 (10): 3033－3038 (in Chinese with English abstract)

[12] 江胜华，周智，欧进萍. 基于磁场梯度张量缩并的岩石断层剪切滑移监测方法[J]. 地下空间与工程学报，2016，12(4)：1014－1020 Jiang Shenghua, Zhou Zhi, Ou Jinping. Deformation monitoring for rock fault shear sliding using magnetic gradient tensor contraction[J].Chinese Journal of Underground Space and Engineering, 2016, 12 (4): 1014－1020 (in Chinese with English abstract)

[13] 江胜华，武立群，侯建国，等. 基于磁性标签石块的桥墩局部冲刷监测方法[J].重庆大学学报，2016，39(1)：88－97 Jiang Sheng-hua, Wu Liqun, Hou Jianguo, et al. Bridge local scour monitoring using magnetic label rock, Journal f Chongqing University, 2016, 39 (1): 88－97 (in Chinese with English abstract)

[14] 张朝阳，肖昌汉，高俊吉，等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报，2010，18(5)：862－868.Zhang Zhaoyang, Xiao Changhan, Gao Junjie, et al.Experiment research of magnetic dipole model applicability for a magnetic object[J]. Journal of basic science and engineering, 2010, 18(5): 862－868. (in Chinese with English abstract)

[15] Wynn W M. Magnetic dipole localization using the gradient rate tensor measured by a five-axis magnetic gradiometer with known velocity[J]. Proc. SPIE, 1995, 2496, 357－367.

[16] Wiegert R F, Oeschger J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance[C]//Proceedings of MTS /IEEE.Washington, DC,2005, 1325－1332.

[17] 江胜华，申宇，褚玉程. 基于磁偶极子的磁场梯度张量缩并的试验验证及相关参数确定[J]. 中国惯性技术学报，2015，23(1)：103－106，114.Jiang Shenghua, Shen Yu, Chu Yucheng. Experimental verification and related parameter’s determination for magnetic gradient tensor contraction using magnetic dipole[J].Journal of Chinese Inertial Technology, 2015, 23(1): 103－106, 114 (in Chinese with English abstract)

[18] 江胜华，侯建国，何英明，等. 基于磁偶极子的磁场梯度张量局部缩并及试验验证. 中国惯性技术学报，2017，25(4)：473－477.Jiang Shenghua, Hou Jianguo, He Yingming, et al.Theoretical study and experimental verification of magnetic gradient tensor partial contraction using magnetic dipole[J].Journal of Chinese Inertial Technology, 2017, 24(4): 473－477 (in Chinese with English abstract)

[19] Espinosa F E C, Torres P, Feyen J. Experimental assessment of the sprinkler application rate for steep sloping fields[J].Journal of Irrigation & Drainage Engineering, 2007, 133 (3):276－278.

[20] 左自波，张璐璐，王建华. 降雨触发不同级配堆积体滑坡模型试验研究[J]. 岩土工程学报，2015，37(7)：1319－1327.Zuo Zibo, Zhang Lulu, Wang Jianhua. Model tests on rainfall-induced colluvium landslides: Effects of particle-size distribution[J]. Chinese Journal of Geotechnical Engineering,2015, 37(7): 1319－1327 (in Chinese with English abstract)

[21] 王静，施斌，严珺凡等. 基于光纤光栅传感器的灾变滑坡模型试验研究[J]. 工程地质学报，2012，20(增刊)：810－815 Wang Jing, Shi Bin, Yan Junfan, etal. Model test of landslides catastrophe based on Fiber Brag Grating sensors[J].Journal of Engineering Geology, 2012, 20(Supp.): 810－815(in Chinese with English abstract)

[22] 曹建建，邓安. 离心加载有限元方法在边坡稳定分析中的应用[J]. 岩土工程学报，2006，28(增刊1)：1336－1339 Cao Jianjian, Deng An. Centrifugal loading finite element method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(Supp.1): 1336－1339 (in Chinese with English abstract)

[23] 卢坤林，朱大勇，杨扬. 边坡失稳过程模型试验研究[J]. 岩土力学，2012，33(3)：778－782.Lu Kunlin, Zhu Dayong, Yang Yang. Model test study of slope failure progress[J]. Rock and Soil Mechanics, 2012,33(3): 778－782 (in Chinese with English abstract)

[24] 吴剑，张振华，王幸林，等. 边坡物理模型倾斜加载方式的研究[J]. 岩土力学，2012，33(3)：713－718.Wu Jian, Zhang Zhenhua, Wang Xinglin, et al. Study of inclined loading mode on slope in physical model test[J].Rock and Soil Mechanics, 2012, 33(3): 713－718 (in Chinese with English abstract)

[25] 卢坤林，朱大勇. 坡面形态对边坡稳定性影响的理论与试验研究[J]. 岩石力学与工程学报，2014，33(1)：35－42.Lu Kunlin, Zhu Dayong. Theoretical and experimental study of effect of slope topography on its stability[J]. Chinese Journal of Rock Mechanics & Engineering, 2014, 33(1): 35－42 (in Chinese with English abstract)

[26] 马俊伟，胡新丽，唐辉明等. 基于计算机辅助检测技术的滑坡模型试验坡面位移场测量[J]. 岩土力学，2013(增刊2)：477－485.Ma Junwei, Hu Xinli, Tang Huiming, et al. Surface displacement field measurement for landslide model test based on computer aided inspection[J]. Rock and Soil Mechanics, 2013(Supp.2): 477－485 (in Chinese with English abstract)

[27] 夏浩，雍睿，马俊伟. 推移式滑坡模型试验推力加载方法的研究[J]. 长江科学院院报，2015，32(1)：112－116.Xia Hao, Yong Rui, Ma Junwei. Method of driving force loading in model test of landslide caused by thrust load[J].Journal of Yangtze River Scientific Research Institute, 2015,32(1): 112－116 (in Chinese with English abstract)

[28] 刘悦，黄强兵. 模拟堆载作用的黄土边坡土体变形机理试验[J]. 地球科学与环境学报，2007，29(2)：183－187.Liu Yue, Huang Qiangbing. Test study for simulating soil deformation mechanism of loess slope under load condition[J]. Journal of Earth Sciences and Environment,2007, 29(2): 183－187 (in Chinese with English abstract)

[29] 李宏杰，戴福初，李维朝，等. 220kV盐津变电所填土边坡稳定性研究[J]. 岩土力学，2008，29(12): 3459－3465.Li Hongjie, Dai Fuchu, Li Weichao, et al. Stability study of a fill slope at 220 kV Yanjin substation[J]. Rock and Soil Mechanics, 2008, 29(12): 3459－3465 (in Chinese with English abstract)

[30] 张月英. 基于改进不平衡推力模式的边坡稳定性分析及程序实现[D]. 长沙：湖南大学，2007.Zhang Yueying. Stability Analysis of Slope Based on Improved Imbalance Thrust Force Method and the Realization of Its Program[D]. Changsha: Hunan University,2007 (in Chinese with English abstract)