考虑冻土双向冻胀与衬砌板冻缩的大型渠道冻胀力学模型

肖 旻，王正中,3※，刘铨鸿，王 羿，葛建锐，王兴威

（1. 西北农林科技大学水利与建筑工程学院，杨凌 712100；2. 西北农林科技大学旱区寒区水工程安全研究中心，杨凌 712100；3. 中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室，兰州 730000）

0 引 言

近年来，大型渠道在中国北方灌区续建配套、节水改造工程和长距离跨流域调水工程中得到广泛应用，然而渠道在冬季极易遭受冻胀破坏[1]。众多学者对渠道冻胀破坏机理进行了研究。如王正中等对梯形与弧底梯形渠道[2-3]、申向东等对预制板梯形渠道[4]，宋玲等[5]对冬季输水的渠道分别提出冻胀力学模型，但均未考虑冻土双向冻胀与衬砌板冻缩应力的影响。冻土双向冻胀是指土体在冻结过程中除沿温度梯度方向存在冻胀以外（法向冻胀），垂直温度梯度方向也会发生冻胀（切向冻胀）[6-8]。对大型渠道而言，由于渠坡较长，切向冻胀不可忽视。Michalowski等[9-10]基于孔隙率模型用体积应变张量表征冻土冻胀纵横向差异，体现冻土的双向冻胀；王正中等[11]对扩大墙基的冻胀力学分析考虑了冻土双向冻胀的影响；Feng等[12-13]考虑寒区隧道衬砌与围岩接触界面层上法向和切向的冻胀作用导出冻胀应力和应变的解析解；蔡海兵等[14-15]通过引入冻胀变形特征系数表征冻土的双向冻胀差异，并对冻结期隧道的地层位移进行计算；Amanuma等[16]通过三轴土体冻胀试验对垂直温度梯度方向的侧压进行研究，指出对冻土纵横 2个方向上的冻胀进行综合分析对工程冻胀破坏分析具有重要意义。此外，有研究表明[17-20]，大型混凝土板结构中由于温度变化引起的材料胀缩受地基约束而产生的应力是不可忽略的，因此，大型渠道衬砌的冻缩应力也是必须考虑的。

该文把大型渠道衬砌板在负温条件下的冻胀破坏视为冻土冻胀与衬砌板冻缩共同作用的结果，结合Winkler假设，考虑冻土冻胀变形的双向冻胀差异，提出开放系统梯形渠道衬砌板法向冻胀力和切向冻胀力分布的计算方法。基于此，本文针对开放系统大型现浇混凝土衬砌渠道，综合考虑冻土双向冻胀和衬砌板冻缩的影响建立渠道冻胀力学模型。

1 开放系统大型梯形衬砌渠道的冻胀特征

开放系统渠道是指因地下水位较浅使基土冻结过程中存在明显水分补给的衬砌渠道[21-22]。与一般渠道相比，旱寒区开放系统大型渠道具有以下冻胀特征：

1）对开放系统渠道，地下水补给是影响土体冻胀强度的主导因素。即使渠道基土初始含水率较低时冻胀也依然严重，且越靠近渠坡下部，冻胀强度受地下水的影响越大，分布越不均匀；越靠近渠坡上部，冻胀强度受地下水的影响越小，基土冻胀强度较小且趋于均匀分布。

2）寒区工程结构受切向冻胀力作用的实质是冻土冻胀受侧向约束产生反作用力[23]。中小型渠道由于渠坡较短，冻土在平行坡板方向上冻胀变形的累积效应较弱，因此在已有研究中较少考虑。但大型渠道渠坡较长，切向冻胀沿平行衬砌板方向的累积效应不可忽略。需要指出的是，冻土与衬砌板界面层上的冻土切向冻胀受上覆土体和衬砌板的双重约束，其中被衬砌板约束的冻胀才实际产生切向冻胀力，因此在计算衬砌板所承受的切向冻胀力时应按其受上覆土体自重进行折减。

3）开放系统渠道基土冻结过程中存在明显的沿温度梯度方向的水分迁移。加之季节冻土区冬季漫长，基土冻结缓慢，更有利于层状冰的形成（图1）[23-26]，其冻胀变形表现为正交各向异性即双向冻胀差异[8-11,14-15,27]。因此，开放系统渠道冻胀破坏研究须考虑冻土在 2个正交方向上冻胀强度的差异。渠道断面呈槽形，渠基冻土温度场即等温线分布也呈槽形，且在冻深范围内各条等温线之间可以近似地认为互相平行且平行于衬砌板[28-29]。

图1 渠基冻土的层状冰构造Fig.1 Structure of ice interlayer in canal foundation frozen soil

4）对大型渠道而言，除外荷载引起的截面应力外，衬砌板的冻缩应力也不可忽略。此处冻缩应力是指负温下衬砌板冻缩受渠基土切向约束产生的温度应力[17-20]。

5）大型渠道断面尺寸及渠深大，在非南北走向时阴、阳坡差异明显，冻胀力学分析必须对阴、阳坡加以区分。

2 力学模型的基本假设和计算简图

2.1 基本约定和假设

结合已有研究成果和工程经验[2-5]，作如下假设：1）渠道纵向尺寸远大于横向尺寸，对渠道衬砌的冻胀力学分析简化为二维平面应变问题。

2）由于冬季漫长，渠道基土冻结速率缓慢，衬砌结构的冻胀破坏过程视为准静态过程，破坏前处于平衡状态，破坏时则处于极限平衡状态。

3）把渠基冻土视为服从 Winkler假设的弹性地基[30-32]，即衬砌上各点所承受的冻胀力大小仅由各点对应处渠基冻土局部的冻胀特征决定，从而在特定地区特定气象、土质条件下，可以认为衬砌板各点对应处渠基冻土的冻胀强度由该点至地下水位的距离确定。

4）渠道坡板上的切向冻结力沿坡板呈线性分布，在坡顶处为0，坡脚处达到最大值[2-4]。

5）仅考虑上覆土体重力导致的沿平行衬砌板方向切向冻胀力的折减，暂不考虑上覆土体冻胀导致下部土体压实引起的进一步折减，这是偏安全的。

2.2 计算简图

根据工程力学方法对渠道衬砌结构进行冻胀力学分析，计算简图见图2。图2a为大型梯形渠道断面示意图。图2b为坡板受力计算简图，图中A点为坡顶，B点为坡脚，q(x)为分布在坡板底部的法向冻胀力，方向为垂直板向外；μ(x)为分布在坡板底部的切向冻胀力，方向为自坡脚沿渠坡指向渠顶；τ(x)为分布在坡板底部的切向冻结力，方向为自渠顶沿渠坡指向坡脚。图2c为底板受力计算简图，qe为分布在底板底部的法向冻胀力，方向为垂直板向外。阴、阳坡坡板计算简图均由图2b表示。变量下标i为m时为阴坡，为s时为阳坡，为e时为渠底。

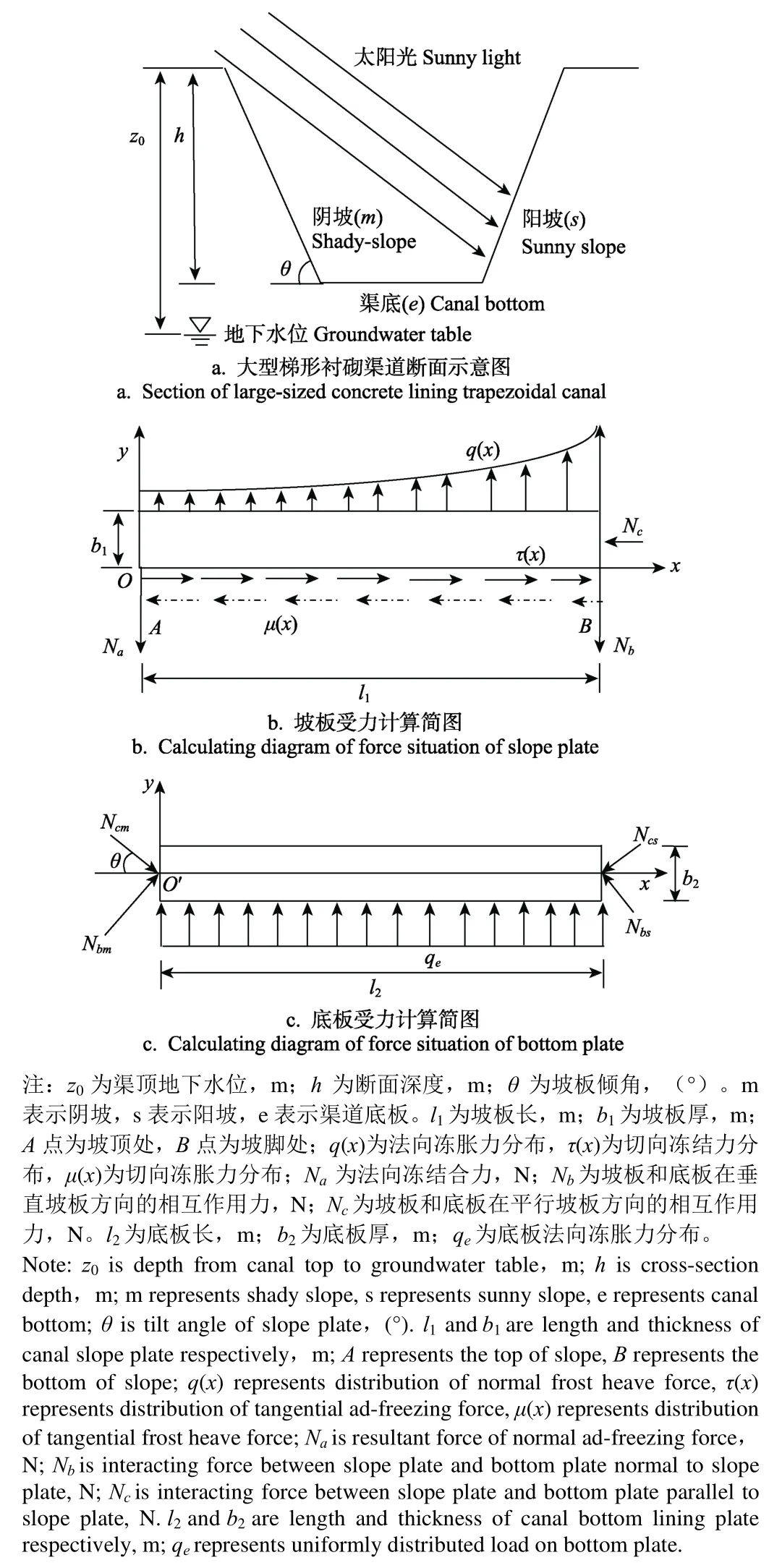
图2 大型梯形衬砌渠道断面示意图与受力计算简图Fig.2 Diagrammatic drawing of section and force situation of large-sized concrete lining trapezoidal canal

对坡板（图2b）与底板（图2c）分别建立坐标系，坡板中以O点为原点，平行坡面指向坡脚处为x轴方向，垂直坡板向外为y轴方向；底板中以O′点为原点，平行底板向右为x轴方向，垂直底板向上为y轴方向。

3 衬砌板法向冻胀力和切向冻胀力的计算

3.1 法向冻胀力的计算

中国北部如新疆、甘肃等大多数省区的相关部门都设置大型冻胀试验场观测地下水位对各类土质基土冻胀强度的影响[23]。大量文献和试验研究表明[22-23,28,33-36]，冻土冻胀强度（即冻胀率）与地下水位呈如下负指数关系

式中 ηn为冻土垂直衬砌板方向（即平行温度梯度方向）的法向冻胀强度，%；z为计算点与地下水位间的距离，m；a、b为与当地气象、土质等影响因素有关的经验系数，可由当地试验数据用最小二乘法拟合获取。

前已述及，对开放系统渠道而言，特定地区特定气象、土质条件下，地下水迁移和补给强度是引起衬砌各点冻土冻胀强度差异的主导因素。基于此，由式（1）可得衬砌各点对应基土冻胀强度公式如下

式中x为衬砌板各点的坐标（坐标系见图2），m；ηn(x)为衬砌各点对应处冻土的法向冻胀强度，%；z(x)为衬砌各点至地下水位的距离，m。

由式（2）可知衬砌各点对应基土冻胀强度与至地下水位的距离呈负指数分布，该分布前段变化快而后段趋于均匀变化且数值较小。从而受地下水影响较大的渠坡中下部对应函数前段变化快的部分[22-23,28,33-36]；受地下水影响很小的渠坡上部则正好对应后段数值较小但趋于均匀变化的部分。可见无论地下水影响较大的区域还是地下水影响很小的区域，式（2）都能很好地进行描述。由假设3）及木下诚一提出的冻胀力与冻胀率的线性关系[22-23,37-38]，衬砌各点法向冻胀力由式（3）计算。

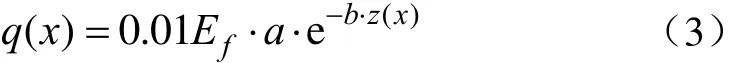
式中q(x)为衬砌各点法向冻胀力，kPa；Ef为冻土弹性模量，kPa。对坡板而言有如下几何关系

式中z0为渠顶至地下水位的距离，m。对底板而言，板上各点至地下水位的距离z(x)为常数。

3.2 切向冻胀力的计算

土冻结时平行和垂直温度梯度方向的冻胀强度存在差异，在气象、土质等因素确定时两者存在一定的函数关系。Michalowski等[9-10]应用孔隙率模型用增长张量按比例分配权重对冻土纵横向冻胀率差异进行描述；黄继辉等[13]通过引入围岩纵横向冻胀不均匀系数表示两者的比例关系；Kanie等[39]对Fujinomori黏土的相关测试也发现同组土样纵横向冻胀率有相同比值。参考上述研究，假定冻土与衬砌板接触界面层上平行和垂直衬砌板方向上的冻土冻胀强度存在如下比例关系

式中ηt(x)为冻土平行衬砌板方向（即垂直温度梯度方向）的切向冻胀强度，%；υ为比例系数，可对特定地区的特定土质进行相关试验获取。如王正中、沙际德等[11,40]对兰州黄土的试验结果表明，该地区该土质条件下式（5）定义的比例系数υ可取为0.422。

加拿大学者Penner依据Linell-Kaplar公式[41]导出了一种计算外压力荷载作用下冻土冻胀强度的计算方法[23,36-37,42-43]，该公式可以反映上覆土体重力荷载作用导致冻土冻胀强度的折减。公式如下

式中 η为外压力荷载 p作用下的冻土冻胀强度，%；η0为无外荷载时冻土的自由冻胀强度，%；c为与当地气象、土质条件有关的经验系数。其中e-cp可视为外压力作用下冻土冻胀强度的折减系数。

为简化分析，认为折减后渠基冻土剩余的冻胀强度全部由衬砌板约束并产生切向冻胀力，这是偏安全的。由此再结合式（5）、式（6），则衬砌板上各点受到的切向冻胀力可以由下式计算

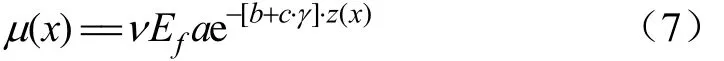
式中γ为土体容重，kN/m3。

4 考虑冻土双向冻胀的渠道冻胀力学模型

4.1 模型方程组的建立与求解

在冻胀力作用下，包括阴、阳坡板受到的法向冻结力 Nam、Nas和切向冻结力 τm(x)、τs(x)；阴坡与底板间垂直于坡板的相互作用力 Nbm及平行于坡板的相互作用力Ncm；阳坡与底板间垂直于坡板的相互作用力 Nbs及平行于坡板的相互作用力Ncs。模型共有8个未知量需要求解。

Ncm、Ncs主要由底板对坡板的顶托力产生，常表现为轴向压力。为便于分析，取预设方向为负值，但其余荷载仍取预设方向为正值。分别由阴、阳坡板和底板的静力平衡条件可得模型方程组如下

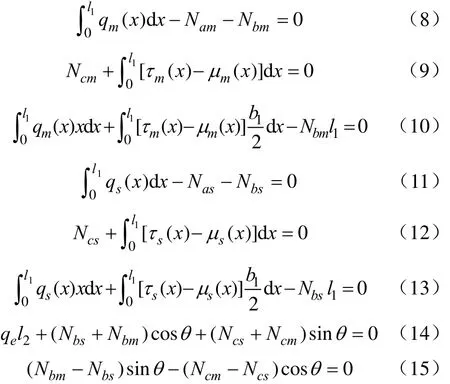
以上各式中l1和b1分别为渠道坡板的长度和厚度，m；l2为渠道底板的长度，m；qe为渠道底板受到的法向冻胀力，kPa；θ为渠道坡板的倾角，（°）。联立以上8个方程可以对前述的8个未知量进行求解。

式中 τm(l1)、τs(l1)为坡板最大切向冻结力，kPa。由式（14）～式（21）可求出前述8个未知量，从而模型得解。

4.2 衬砌板内力计算

1）以阴坡为例，导出渠道坡板内力计算公式渠道坡板各截面的轴力计算公式

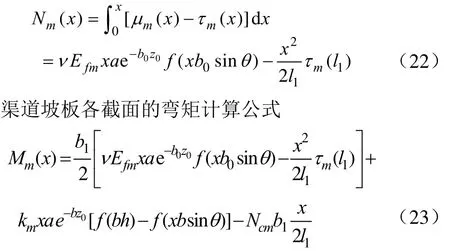
考虑到 h=l1·sinθ并结合式（16）可知渠道坡板两端弯矩Mm(0)=Mm(l1)=0，这与已有研究结果一致[2-3]。

2）渠道底板的内力计算公式

渠道底板各截面轴向内力为压力，而混凝土材料的抗压能力较强，衬砌板通常不会因压应力过大而发生破坏[2-5]，故可不予验算。现仅对渠道底板各截面弯矩进行计算，计算公式如下

式中xemax为渠底最大弯矩截面的坐标，m。

以上为考虑阴、阳坡差异的一般模型，理论上在非南北走向时均应考虑阴、阳坡差异，而对南北走向的特殊情形可以不区分阴、阳坡。当采用不区分阴坡和阳坡的对称模型时，由式（14）可得下式

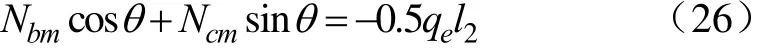
代入式（25）可得渠底最大弯矩截面为xemax=0.5l2，符合已有研究结果[2-3]及工程实际。

5 衬砌板冻缩的温度应力计算及抗裂验算

5.1 衬砌板冻缩的温度应力计算

负温下衬砌板冻缩变形受到冻土切向约束并阻止其变形，会在板内产生温度应力[17-20]。以阴坡为例，把负温下发生冻缩的衬砌板视为受一维切向约束的均匀收缩矩形梁，求解其温度应力分布。此处仅考虑温降导致衬砌板冻缩引起的温度应力，即计算冻缩应力时不考虑其他荷载的影响。由于对称性，坡板中间截面位移为零[17-18]，两侧向中间截面收缩，冻土作用在衬砌板底面的切向约束反力应沿底面指向两端。由于渠道衬砌为薄板结构，可认为负温条件下衬砌板均匀收缩，从而各截面冻缩应力可近似取均匀分布。图3为坡板冻缩的计算简图。全局坐标系见图2b，并如图3所示建立局部坐标系。

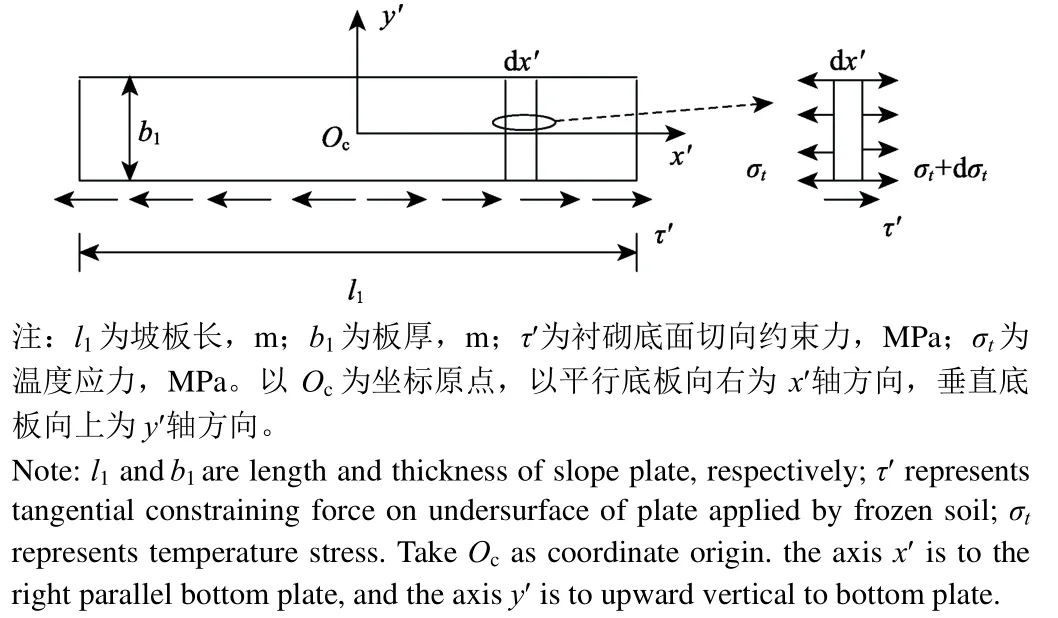
图3 渠道坡板冻缩的计算简图Fig.3 Calculating diagram of frozen shrinkage stress of canal slope plate

考虑如图3右侧所示的长度为dx′的微元体，由水平方向上的静力平衡可得平衡微分方程如下

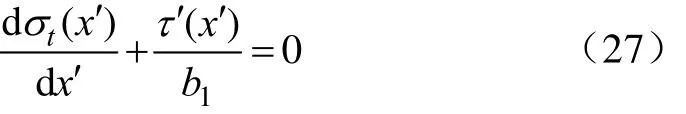
式中 σt(x′)为衬砌板各截面冻缩应力，kPa；τ′(x′)为冻土作用在衬砌板底面的切向约束反力，kPa。

衬砌板各截面同时受衬砌板冻缩和冻土的约束作用时还应满足变形协调条件

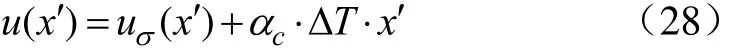
式中热膨胀系数为αc，1/℃；各截面实际水平位移为u(x′)，m；被冻土约束的位移为uσ(x′)，m；ΔT表示温差，℃。

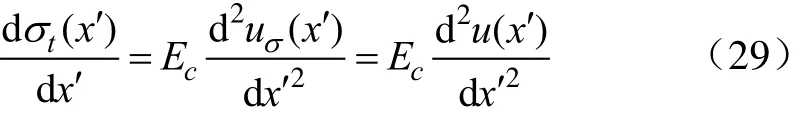
对式（28）两边同时求导两次，并考虑到应力、应变和位移的关系：σt(x′)=Ec·(duσ(x′)/dx′)，其中 Ec为混凝土弹性模量，MPa。则由假设 3），基土为服从 Winkler假设的弹性地基，各点切向约束力 τ′(x′)与相应点实际水平位移 u(x′)成正比，即：τ′(x′)=kx·u(x′)，kx为各点发生单位水平位移时切向约束力大小[17,30-32]。结合式（27）、式（29）可得

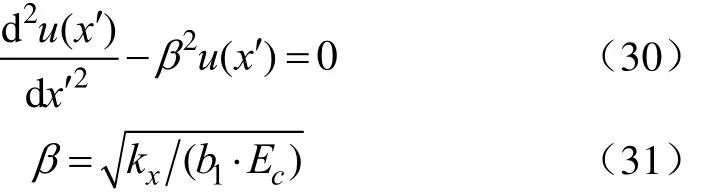
求解式（30）可得其通解的形式如下

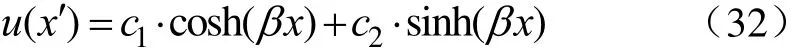
式中c1、c2为待定常数；sinh、cosh为双曲正弦和双曲余弦函数。该式应满足边界条件：当 x′=0时，u(0)=0；当x′= -l1/2 时，σt(-l1/2)=0。由此可解出 c1、c2，从而 u(x´)得解，再由应力、应变和位移间的关系可得阴坡坡板的冻缩应力分布如下

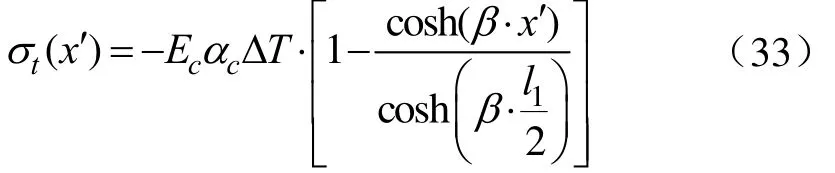
通过坐标变换把上式由如图 3所示的坐标系转换为如图2b所示的整体坐标系，如下

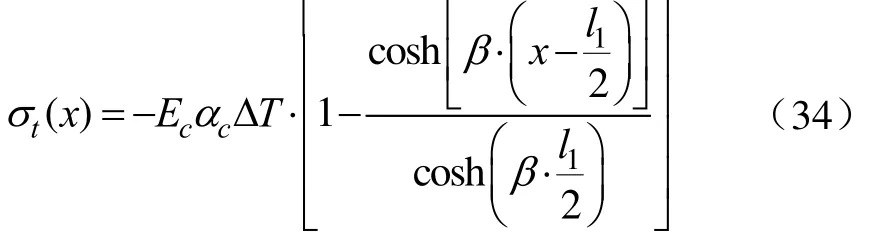
式中l1为渠道坡板长，m。式（33）中的负号表示温差为负即衬砌板冻缩时温度应力为拉力。

5.2 抗裂验算

渠道衬砌板在冻胀作用下为压弯构件，故仅须对衬砌板危险截面的上表面应力进行验算即可[2-3]。由小变形假设即迭加原理，可认为衬砌板各截面上表面应力为以下三者作用效果的迭加：截面轴力、截面弯矩及衬砌板冻缩的温度应力，即

式中 σimax(x)为衬砌板各截面的最大拉应力，即上表面拉应力，kPa；σiN(x)为由截面轴力引起的各截面上表面应力，kPa；σiM(x)为由截面弯矩引起的各截面上表面应力，kPa；σit(x)为冻缩应力，kPa。

冬季寒区衬砌渠道的结构破坏通常表现为截面最大拉应力超过允许应力而导致衬砌板拉裂或折断，因此有必要对危险截面进行抗裂验算，计算公式如下

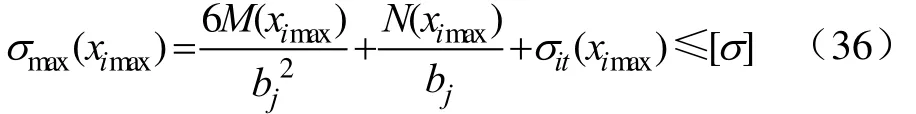
式中 ximax为危险截面的坐标，m；σmax(ximax)为危险截面的最大拉应力，MPa；M(ximax)为危险截面的弯矩，kN·m；N(ximax)为危险截面的轴力（通常为负），kPa；；σit(ximax)为危险截面的冻缩应力，MPa；[σ]为允许应力，MPa；bj为板厚，m。j为1或2时分别表示渠道坡板或底板。

6 工程算例

以甘肃省白银市靖会灌区某混凝土衬砌梯形渠道为例，该地区属温带干旱半干旱气候，越冬期日均最低气温约为-16 ℃。采用C25混凝土衬砌，板厚为0.12 m，地下水位（至渠顶）约为6 m，土质为粉质壤土(即兰州黄土)。渠道阴坡、渠底和阳坡冻土层最低温度分别为-13.21、-9.56和-7.53 ℃。渠道断面尺寸见图4。现对该渠道衬砌结构进行冻胀力学分析。

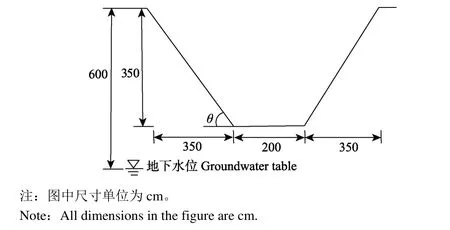
图4 原型渠道断面示意图Fig.4 Sketch map of cross-section of prototype canal

条件具备时，各式经验系数应由当地现场试验数据拟合获取，本文主要通过参考文献取值。相关参数和经验系数见表1[3,23,28,33-36,44]，其中各冻土层弹性模量均按冬季最低温度取值，这是偏安全的。坡角θ为45°。

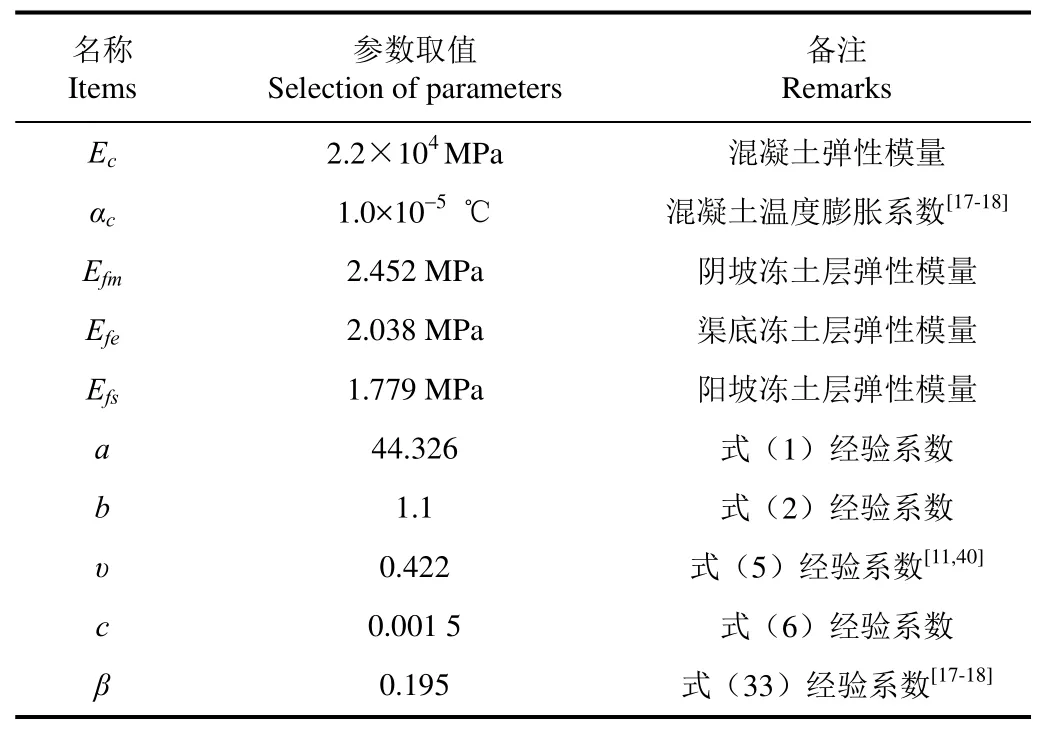
表1 相关参数与经验系数Table 1 Parameters and empirical coefficients

1）模型求解及截面内力的计算

把式（16）～式（21）依次代入可使各未知量均写为τm(l1)和τs(l1)的函数，把结果代入式（14）～式（15）联立求解可得：τm(l1)=52.393 kPa，τs(l1)=49.646 kPa。把τm(l1)、τs(l1)逐次回代到式（16）～式（21）中，则阴、阳坡和渠底衬砌板各自承受的所有外力均可解出。

以渠道阴坡为例，由式（22）可得阴坡坡板各截面的轴力分布

2）衬砌板截面最大拉应力分布及抗裂验算

对渠道衬砌板冻胀破坏的分析应先确定危险截面的位置。为此，须先对衬砌板各截面最大拉应力分布进行计算。仍以阴坡坡板为例，由衬砌板各截面内力计算结果可分别计算轴力引起的截面上表面应力 σmN和弯矩引起的截面上表面应力 σmM沿坡板的分布。又由式（34）可得各截面冻缩温度应力σmt沿坡板分布如式（39）所示。

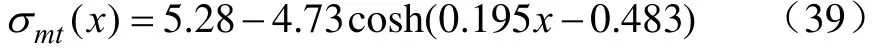
图5为应力σmN、σmM及σmt沿阴坡坡板分布图。

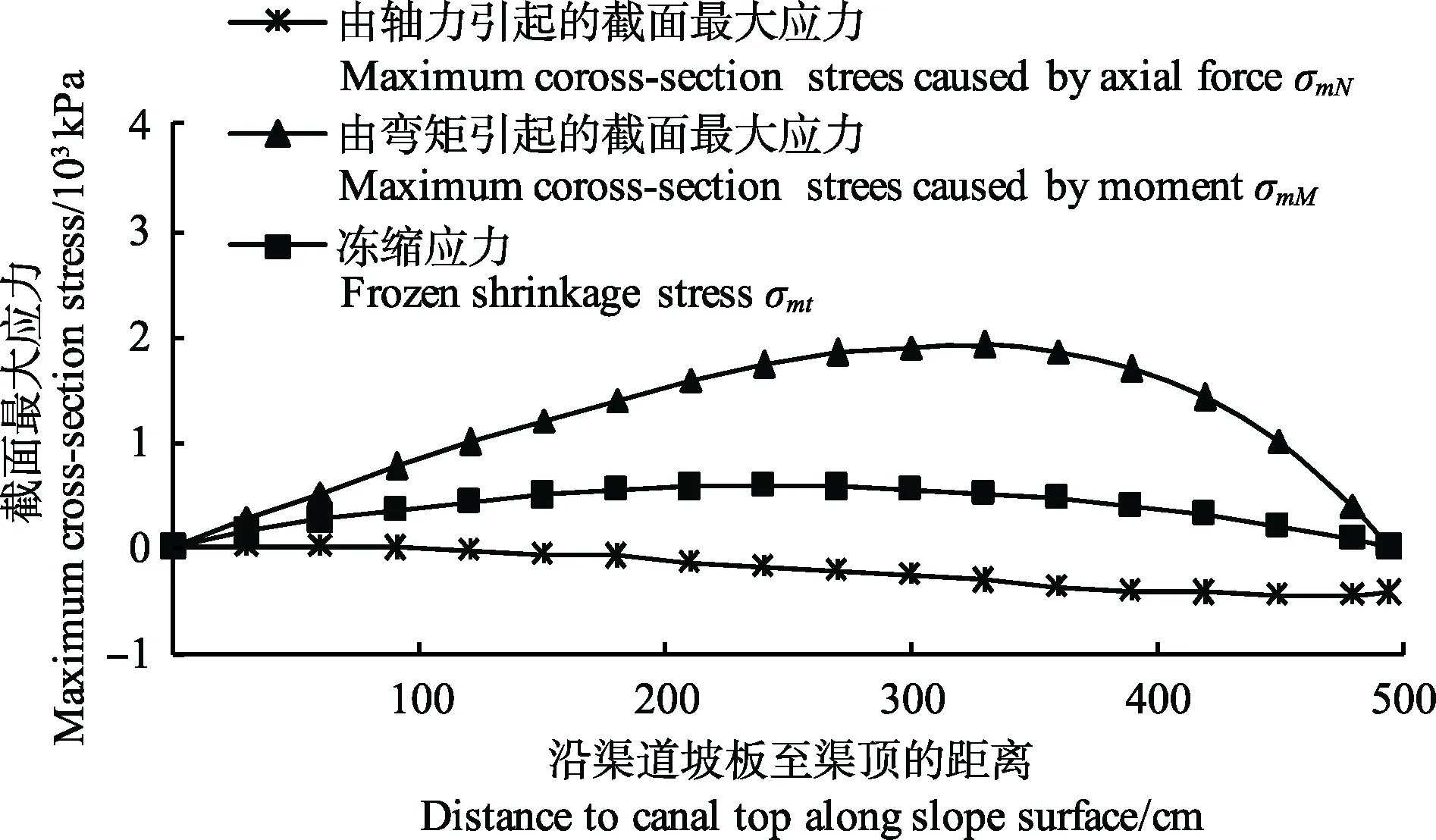
图5 应力σmN、σmM及σmt沿阴坡坡板的分布图Fig.5 Distribution of cross-section stress σmN、σmM and σmt

由图5可知，轴力引起的衬砌板上表面应力σiN为压应力（负值），其分布规律为自坡顶到坡脚逐渐增大；弯矩引起的衬砌板上表面应力 σiM为拉应力（正值），其分布规律为在坡板两端为零，最大值约在距坡脚 1/3板长处，与文献[2-3]已有研究结果相符；冻缩应力σmt为拉应力（正值），其分布规律为自坡顶到坡脚先增大后减小，最大值在坡板中部，与文献[17-18]研究结果一致，即在温度应力单独作用时存在“一再从中部开裂”的现象。综上所述，由迭加原理可得衬砌板各截面上表面应力即最大拉应力的分布规律如下式所示

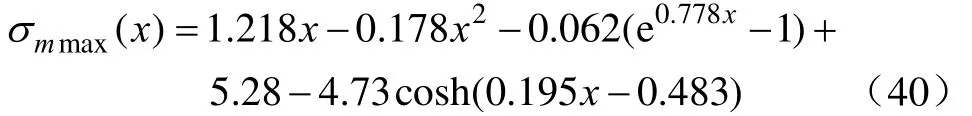
式（40）的极值点即为危险截面的位置。现用二分法求解，预定精度取0.005，二分7次得x=270.634 cm，相应的最大拉应力为σmmax(270.634)=2.134 MPa。

3）对比分析

图 6为阴坡坡板各截面轴力及最大拉应力分布图。图6a为考虑双向冻胀与仅考虑法向冻胀的2种情形下阴坡坡板各截面的轴力分布图。由图6a可知，由于切向冻胀力的作用使坡板各截面产生拉力，从而考虑双向冻胀与仅考虑法向冻胀相比，轴向压力的量值明显减小。由式（35）可知轴向压力越大则最大截面拉应力的计算值越小，即若不考虑切向冻胀力的影响将过高估计轴向压力对拉应力的削减，造成安全隐患。此外，考虑双向冻胀时轴力分布存在明显的拐点，这是因为切向冻胀力与切向冻结力作用效果相反且沿渠坡变化规律不同。由式（7）可知，切向冻胀力沿渠坡从渠顶至坡脚呈指数规律增大（即开始增大缓慢而随后变得很快）；由基本假设4），切向冻结力沿渠坡从渠顶至坡脚线性增大（即保持恒定速率增大）。综上可知，在坡板中上部，切向冻结力线性增大而切向冻胀力变化缓慢，此时切向冻结力占主导作用，使轴力的量值增大；而坡板中下部即靠近坡脚处，切向冻胀力由于指数规律快速增大而切向冻结力仍按恒定速率增大，此时切向冻胀力占主导作用，使轴力的量值转而减小，从而产生拐点。由此可见，渠基冻土双向冻胀对截面轴力乃至最大截面拉应力有明显影响。

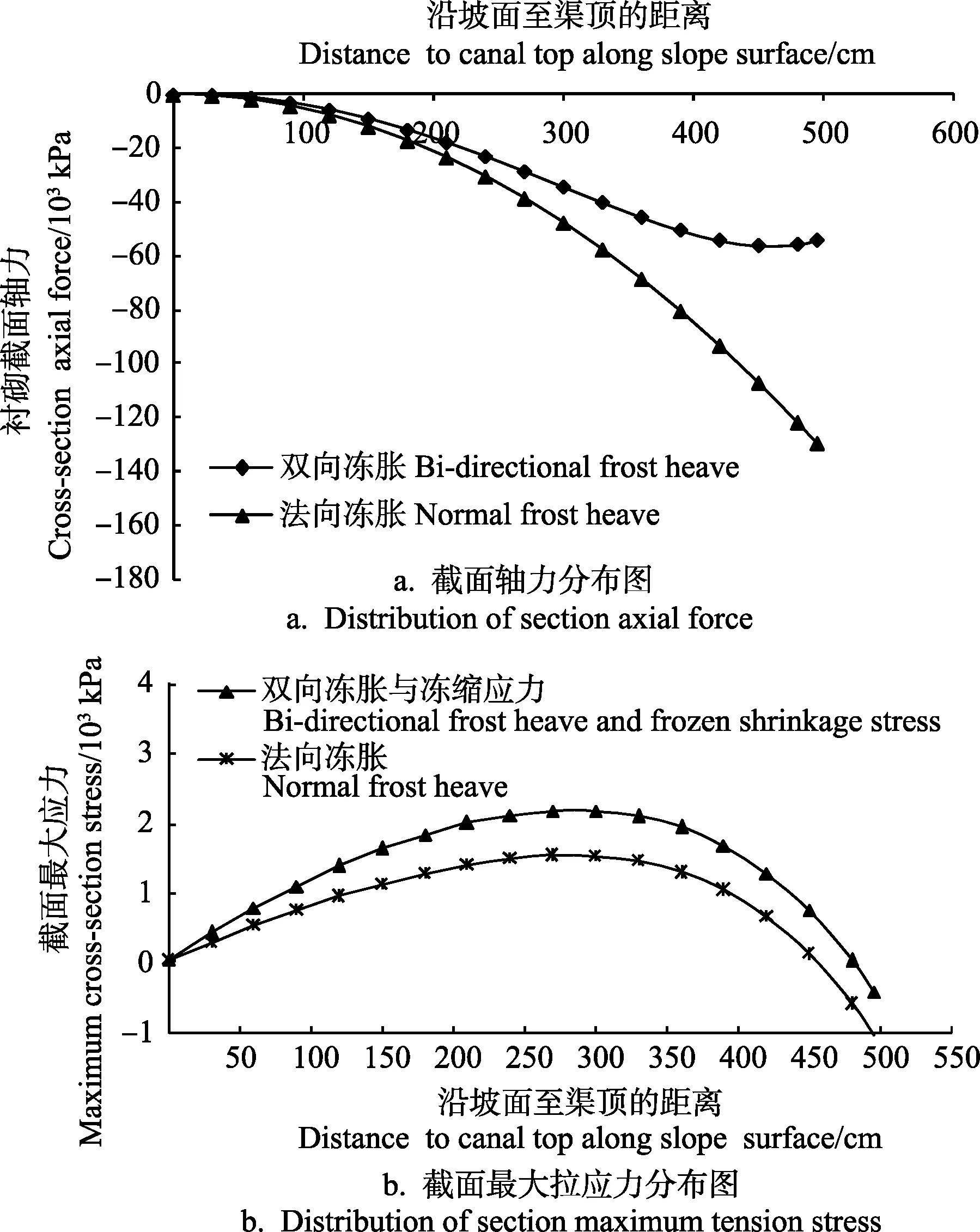
图6 阴坡坡板各截面轴力及最大拉应力分布图Fig.6 Distribution of section axial force and maximum tension stress on canal shady-slope lining plate

图6b为考虑双向冻胀及冻缩应力与仅考虑法向冻胀且不考虑冻缩应力的 2种情形下阴坡坡板各截面最大拉应力分布图。由图6b可知，2种情形下坡板各截面最大拉应力分布趋势大致相同，且坡脚均为压应力（负值），这主要由底板对坡板的顶托力导致。当考虑双向冻胀及冻缩应力影响时，截面最大拉应力极大值为2.134 MPa；当仅考虑法向冻胀且不考虑冻缩应力影响时，截面最大拉应力极大值仅为1.494 MPa，较前者小约30%。由此可见，若仅考虑法向冻胀且不考虑冻缩应力的影响将导致计算值明显偏小，在大型梯形渠道抗冻胀设计中建议综合考虑渠基冻土双向冻胀和衬砌板冻缩应力的影响。

7 结论与讨论

1）把负温下大型渠道衬砌板的冻胀破坏视为由冻土冻胀与衬砌板冻缩共同作用的结果，结合Winkler弹性地基假设，考虑冻土双向冻胀差异，提出一种开放系统梯形渠道衬砌板法向冻胀力和切向冻胀力分布的计算方法。在此基础上建立考虑双向冻胀与衬砌板冻缩的大型渠道冻胀力学模型。

2）把负温下发生冻缩变形的渠道衬砌板视为受一维切向约束的均匀收缩矩形梁，推导了衬砌板冻缩应力表达式，并由迭加原理提出大型渠道衬砌的抗裂验算方法。

3）结合工程算例应用本文模型分析了衬砌板各截面内力和冻缩应力的分布规律，得到了各截面最大拉应力分布规律及危险截面位置。

4）对考虑双向冻胀和冻缩应力及仅考虑法向冻胀的两种情形进行了分析，结果表明：前者截面最大拉应力极大值为2.134 MPa，而后者的相应值仅为1.494 MPa，较前者小约 30%。因此，若仅考虑法向冻胀将导致计算值明显偏小，在大型梯形渠道抗冻胀设计中建议综合考虑冻土双向冻胀和衬砌板冻缩应力的影响。

本文基于小变形假设把冻胀力的作用效果与衬砌板冻缩的作用效果分别计算，再应用迭加原理迭加，暂未考虑衬砌板冻缩受基土约束产生的约束力与切向冻胀力的相互影响。考虑两者耦合作用的模型有待进一步研究。

[参 考 文 献]

[1] 周幼吾，郭东信，邱国庆，等.中国冻土[M]. 北京：科学出版社，2000.

[2] 王正中. 梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2004，20(3)：24－29.Wang Zhengzhong. Estabishment and application of mechanics model of frost heaving damage of concrete lining trapezoidal open canal[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE)，2004, 20(3): 24－29. (in Chinese with English abstract)

[3] 李甲林，王正中. 渠道衬砌冻胀破坏力学模型及防冻胀结构[M]. 北京：中国水利水电出版社，2013.

[4] 申向东，郑玉佩，王丽萍. 混凝土预制板衬砌梯形断面渠道的冻胀破坏受力分析[J]. 农业工程学报，2012，28(16)：80－85.Shen Xiangdong, Zheng Yupei, Wang Liping. Stress analysis of frost heave for precast concrete panel lining trapezoidal cross-section channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2012, 28(16): 80－85. (in Chinese with English abstract)

[5] 宋玲，欧阳辉，余书超. 混凝土防渗渠道冬季输水运行中冻胀与抗冻胀力验算[J]. 农业工程学报，2015，31(18)：114－120.Song Ling, Ouyang Hui, Yu Shuchao. Frozen heaving and capacity of frozen heaving resistance of trapezoidal concrete lining canal with water in winter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 31(18): 114－120. (in Chinese with English abstract)

[6] Taber S. The mechanics of frost heaving[J]. The Journal of Geology, 1929, 38(4): 429－7461.

[7] Areson L U, Springman S M, Sego D C. The rheology of frozen soils[J]. Applied Rheology, 2007, 17(1): 121－147.

[8] 王正中，袁驷，陈涛. 冻土横观各向同性非线性本构模型的实验研究[J]. 岩土工程学报，2007，29(8)：1215－1218.Wang Zhengzhong, Yuan Si, Chen Tao. Study on the constitutive model of transversely isotropic frozen soil[J]Chinese Journal of Geotechnical Engineering, 2007, 29(8):1215－1218. (in Chinese with English abstract)

[9] Michalowski R L. A constitutive model of saturated soils for frost heave simulation[J]. Cold Regions Science and Technology, 1993, 22(1): 47－62.

[10] Michalowski R L, Zhu M. Frost heave modelling using porosity rate function[J]. International Journal for Numerical and Analytical Methods in Geo-mechanics, 2006, 30(8): 702－722.

[11] 王正中，张长庆，沙际德，等. 正交各向异性冻土与建筑物相互作用的非线性有限元分析[J]. 土木工程学报，1999，32(3)：55－60.Wang Zhengzhong, Zhang Changqing, Sha Jide, et al.Nonlinear finite element analysis of interaction of orthotropic frozen ground and construction[J]. China Civil Engineering Journal, 1999, 32(3): 55－60. (in Chinese with English abstract)

[12] Feng Qiang, Liu Weiwei, Jiang Binsong. Analytical solution for the stress and deformation of rock surrounding a cold-regional tunnel under unequal compression[J]. Cold Regions Science and Technology, 2017, 139(1): 1－10.

[13] 黄继辉，夏才初，韩常领，等. 考虑围岩不均匀冻胀的寒区隧道冻胀力解析解[J]. 岩石力学与工程学报，2015，34(增 2)：1667－1676.Huang Jihui, Xia Caichu, Han Changling, et al. Analytical solution of frost heave force acting on cold-region tunnel liner considering anisotropy frost heave of surrounding rock[J]. Chinese Journal of Rock Mechanics and Engineering,2005, 34(Supp.2): 1667－1676. (in Chinese with English abstract)

[14] 蔡海兵，程桦，姚直书，等. 基于冻土正交各向异性冻胀变形的隧道冻结期地层位移数值分析[J]. 岩石力学与工程学报，2015，34(8)：3766－3774.Cai Haibing, Cheng Ye, Yao Zhishu, et al. Numerical analysis of ground displacement due to orthotropic frost heave of frozen soil in freezing period of tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8):3766－3774. (in Chinese with English abstract)

[15] 蔡海兵. 地铁隧道水平冻结工程地层冻胀融沉的预测方法及工程应用[D]. 长沙：中南大学，2012.Cai Haibing. Prediction Methods and Their Engineering Application of Ground Frost Heave and Thawing Settlement in Subway Tunnel Horizontal Freezing Construction[D].Changsha: Central South University, 2012. (in Chinese with English abstract)

[16] Amanuma C, Kanauchi T, Akagawa S, et al. Evaluation of frost heave pressure characteristics in transverse direction to heat flow[J]. Procedia Engineering, 2017(1): 461－468.

[17] 叶琳昌，沈义. 大体积混凝土施工[M]. 北京：中国建筑工业出版社，1987.

[18] Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing: TsingHua University Press，2014.

[19] 王希尧. 关于渠道衬砌冻害的初步分析[J].水利水电技术，1979，11(9)：45－48.

[20] 张国新，彭静. 考虑摩擦约束时面板温度应力的有限元分析[J]. 水利学报，2001，32(11)：75－79.Zhang Guoxin, Peng Jing. Finite element analysis for thermal stress of concrete slabs with friction constraint[J]. Journal of Hydraulic Engineering, 2001, 32(11): 75－79. (in Chinese with English abstract)

[21] 马巍，王大雁. 冻土力学[M]. 北京：科学出版社，2014.

[22] 肖旻，王正中，刘铨鸿，等. 考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型[J]. 水利学报，2017，48(10)：1229－1239.Xiao Min, Wang Zhengzhong, Liu Quanhong, et al. Elastic foundation beam model of frost heave damage of trapezoidal canal considering interaction between frozen soil and lining structure[J]. Journal of Hydraulic Engineering, 2017, 48(10):1229－1239. (in Chinese with English abstract)

[23] 陈肖柏，刘建坤，刘鸿绪，等. 土的冻结作用与地基[M].北京：科学出版社，2006.

[24] Konrad J M, Duquennoi C. A model for water transport and ice lensing in freezing soils[J]. Water Resources Research,1993, 29(9): 3109－3124.

[25] Sheng D, Axelsson K, Knutsson S. Frost heave due to ice lens formation in freezing soils 1. Theory and verification [J].Nordic Hydrolgy, 1995, 26(2): 125－146.

[26] Sheng D, Axelsson K, Knutsson S. Frost heave due to ice lens formation in freezing soils 2. Field application[J]. Nordic Hydrolgy, 1995, 26(2): 125－146.

[27] 王正中，牟声远，牛永红，等. 横观各向同性冻土弹性常数及强度预测[J]. 岩土力学，2008，29(增刊)：475－480.Wang Zhengzhong, Mou Shengyuan, Niu Yonghong, et al.Prediction of elastic constants and strength of transverse isotropic frozen soil[J]. Rock and Soil Mechanics, 2008,29(Supp.): 475－480. (in Chinese with English abstract)

[28] 李安国，李浩，陈清华. 渠道基土冻胀预报的研究[J]. 西北水资源与水工程学报，1993，4(3)：17－23.Li Anguo, Li Hao, Chen Qinghua. Study on the prediction of frost heave in the bedsoil of canals[J]. Water Resources &Water Engineering, 1993, 4(3): 17－23. (in Chinese with English abstract)

[29] 刘月，王正中，王羿，等. 考虑水分迁移及相变对温度场影响的渠道冻胀模型[J]. 农业工程学报，2016，32(17)：83－88.Liu Yue, Wang Zhengzhong, Wang Yi, et al. Frost heave model of canal considering influence of moisture migration and phase transformation on temperature field[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(17): 83－88. (in Chinese with English abstract)

[30] Selvadural A P S. Elastic Analysis of Soil-Foundation Interaction[M]. New York: Elsevier Scientific Publishing Company, 1979.

[31] 龙驭球. 弹性地基梁的计算[M]. 北京：人民教育出版社，1981.

[32] 李方政. 土体冻胀与地基梁相互作用的叠加法研究[J]. 岩土力学，2009，30(1)：79－85.Li Fangzheng. Research on superposition method of interaction between soil frost heave and beams on foundation[J]. Rock and Soil Mechanics, 2009, 30(1): 79－85. (in Chinese with English abstract)

[33] 王希尧. 不同地下水埋深和不同土壤条件下的冻结和冻胀试验研究[J]. 冰川冻土，1980，3(2)：40－45.Wang Xiyao. Expermental research of frost heave under different level of groundwater in various soils[J]. Journal of Glaciology and Geocryology, 1980, 3(2): 40－45. (in Chinese with English abstract)

[34] 徐学祖. 中国冻胀研究进展[J]. 地球科学进展，1994，9(5)：13－18.Xu Xuezu. Progress of frost heave research in china[J].Advance in Earth Sciences, 1994, 9(5): 13－18. (in Chinese with English abstract)

[35] 山西省渠道防渗工程技术手册编委会. 山西省渠道防渗工程技术手册[M]. 太原：山西科技出版社，2003.

[36] 安鹏，邢义川，张爱军. 基于部分保温法的渠道保温板厚度计算与数值模拟[J]. 农业工程学报，2013，29(17)：54－62.An Peng, Xing Yichuan, Zhang Aijun. Thickness calculation and numerical simulation of insulation board for canal using partial insulation method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(17): 54－62. (in Chinese with English abstract)

[37] 周长庆. 关于法向冻胀力计算方法的讨论[J]. 冰川冻土，1981，3(2)：28－23.

[38] 木下诚一. 冻土物理学[M]. 王异，张志权译.长春：吉林科学技术出版社，1985.

[39] Kanie S, Hao Z, Makimura M, et al. A practical method for three-dimensional frost heave simulation based on takashi’s equation[C]//Proceedings of the 15thInternational Specialty Conference on Cold Regions Engineering, August 19－22,2012, American Society of Civil Engineers, Quebec City:ASCE, c2012: 697－704.

[40] 沙际德，张长庆，王正中，等. 粉土自由冻胀参数的实验研究[C]//中国科学院兰州冰川冻土研究所. 第五届全国冻土学术会议论文集，北京：科学出版社，1996：1201－1207.Sha Jide, Zhang Changqing, Wang Zhengzhong. Testing parameters of frozen soil[C]//Lanzhou Institute of Glaciology and Geocryology, Chinese Academy of Sciences, Proceeding of the 5th permafrost congress of china, Beijing: Science Press: 1201－1207. (in Chinese with English abstract)

[41] Linell K A, Kaplar C W. The factor of soil and material type in frost action[J]. Highway Research Board Bulletin, 1959,225(1): 81－125.

[42] Penner E. Frost heaving forces in leda clay[J]. Canadian Geotechnical Journal, 1970, 7(8): 8－16.

[43] Chen Xiaobai, Wang Yaqing. Frost heave prediction for clayey soil[J]. Cold Regions Science and Technology, 1988,15(1): 233－238.

[44] 张钊，吴紫汪. 渠道基土冻结时温度场和应力场的数值模拟[J]. 冰川冻土，1993，15(2)：331－338.Zhang Zhao, Wu Ziwang. Numerical analysis of temperature and stress on the canal subsoil during freezing[J]. Journal of glaciology and geocrology, 1993, 15(2): 331－338. (in Chinese with English abstract)