Robust edge-preserving surface mesh polycube deformation

Hui ZhaoNa Lei()Xuan LiPeng ZengKe Xuand Xianfeng Gu

The Author(s)2017.This article is published with open access at Springerlink.com

1 Introduction

Polycubes are special geometric shapes,whose face normals are aligned with the one of the six axis directions of a prescribed orthonormal coordinate frame.A polycube may be used to capture overall and global shape features of a mesh,and remove its local details.

The idea of a polycube was first proposed in Ref.[1]to extend cube mapping to general shapes.These special shapes generalize geometry images[2], and allow geometry and texture to be stored efficiently.Due to their highly regular structure and special global parametric domain,polycubes are useful in many graphics applications, such as surface texturing [1],volume texturing [3], parameterization [4,5],reconstruction [6],hexahedral remeshing [7–10],shape morphing[11],spline construction[6,12],volumetric mapping [13, 14], and T-mesh construction[15].

Constructing polycube shapes from meshes is a challenging problem. In early works,polycube meshes were constructed manually[1,5],which needs a lot of tedious,labor-intensive user interaction requiring great care.After the polycube has been constructed,another extra algorithm was needed to determine the cross-surface map between the polycube and the mesh[12].Determining this map is also a challenging problem in itself[6].If we change the polycube,we need to rebuild the map.

In this paper,we propose a novel,automatic polycube deformation algorithm which can be applied to a surface mesh.Our method separates the polycube construction process into three explicit components: segmentation,polycube topology determination,and polycube geometry construction.Our major contribution is to the polycube geometry step.We propose a deformation method based on face normal rotation.The technique we implement can process all kinds of meshes,of varying genus,orientated or non-orientated,and with or without boundaries.Compared to previous methods,our algorithms is more efficient,robust,fast,accurate and can deform a mesh with complicated geometry and arbitrary topology into a corresponding polycube. Pre-processing and post-processing are not required,and there are no topological degeneracies in our experimental results. As the polycubes are resulted by deforming the original meshes,we automatically determine a direct cross surface parameterization between the meshes and their corresponding polycube shapes.

2 Related work

Recently,some automatic polycube construction algorithms have been proposed in Refs.[7,16–18].The authors use a segmentation method to patch the input mesh,then use box-primitives to approximate it coarsely in Ref.[18],but this method fails for complicated models.The method in Ref.[18]applies distance-based,divide-and-conquer algorithms to build the polycube,while the one in Ref.[16]generates over-refined polycubes and is sensitive to off-axis features.The algorithms in Refs.[16,18]are based on surface meshes and can not build the cross-surface map automatically.While the algorithms in Refs.[7,17]are volume-mesh-based,they look for the specific polycube which minimizes the distortion of the volumetric map.

A polycube is an axis aligned shape which mimics the original shape,but with the geometric characterization that each of its face normals is aligned with one of the axes of a given orthonormal coordinate frame.Therefore,the value of theℓ1-norm of every unit face normal of the polycube shape is equal to 1[17].Based on this observation,Ref.[17]defines anℓ1-norm energy which is weighted by triangle area,then proposes a variational method to deform an input triangle mesh into a polycube shape by minimization of this energy.Theℓ1-norm term of the mesh’s face normals,and the weight term of triangle areas are both non-linear in mesh position. The authors change the unconstrained system into a constrained minimization problem to make it well-behaved,numerically tractable,and efficient.Finally,a complicated numerical method is resorted to solve the minimization problem in Ref.[17].To decrease distortion,a volumetric mesh is created from the surface mesh,then an as-rigidas-possible volumetric distortion energy[19]is used to regularize the system.There are many minima of the deformation energy,so a regularization approach is also used to single out the desired polycube[17].

Because the polycube results differ according to axis orientation,the authors also introduce an energy term to find the optimal global orientation for the polycube.This energy is integrated into their whole system. However,the optimal polycube over all orientations is an ill-defined concept. We do not think there should be an optimal polycube.

The polycubes resulting from the above approach often have spurious topological degeneracies.A postprocessing cleanup step is used to fi x the problem in Ref.[17].

Their method also requires that the input mesh is closed,while our method can process meshes with open boundaries.

Themethod in Ref.[7]aimstoalign the surface normals of an input mesh with one of six axes(±X,±Y,±Z)gradually,in a step called rotation-driven deformation. However the result is not a perfect polycube and a second positiondriven deformation is required to exactly align each polycube face with the corresponding axis,and to enforce planarity.Our method is similar to theirs,but our algorithms use different methods to compute rotations.As a result,our results converge to planar faces and we do not need post-processing steps.

The algorithm in Ref.[20]requires an existing polycube,which they then optimize to meet a desired quality. The method in Ref.[9]attacks the polycube segmentation problem using a graph cut-based approach to achieve a polycube base complex which satisfies certain quality requirements.The algorithms balance parameterization distortion against the number of singularities of the polycube.We use the same segmentation step as theirs[9,21],but suggest a different polycube geometry deformation method from theirs.

Another polycube method similar to ours is given in Ref.[21]. Their algorithm is also a normal driven method.Given a polycube with complicated topology,a simplification method is proposed in Ref.[22].

Poisson-system-based deformation[23]is a well known technique. After rotations of all triangle faces have been determined,the triangles can be rotated into the new orientation,and then a Poisson system is used to blend the triangle soup together and reconstruct a consistent mesh into its new shape.The rotations can be computed according to application needs. In Ref.[24],the rotation is achieved by interpolation from two meshes in correspondence. In Ref.[25],rotations of the triangles are interpolated.

3 Algorithms

3.1 Preliminaries

Apolycubeis a shape formed by joining several rectangular faces together in such a way that the surface normals of the polycube are axis-aligned.A polycube has also been called an orthogonal polyhedron[9,26].We observe that there are three steps in deforming a mesh into a corresponding polycube shape:segmentation,polycube topology determination,and polycube geometry construction.These three steps can be made independent of each other.The first step divides a mesh into several different charts. The second step determines the polycube topology of the mesh,and the third step fi xes the polycube geometry.Figure 1 shows two models which are segmented into parts in the second column.Using the parts,each model’s polycube topology is found as shown in the third column,and finally our algorithm obtains an exact polycube geometry as shown in the last column. Many previous algorithms combine these two or three steps into one.Our algorithm separates them explicitly.In this paper,we focus on the polycube geometry construction step. Given a model with a valid polycube topology,found,e.g.,using the method in Ref.[21],our algorithm produces a final shape with perfect polycube geometry.

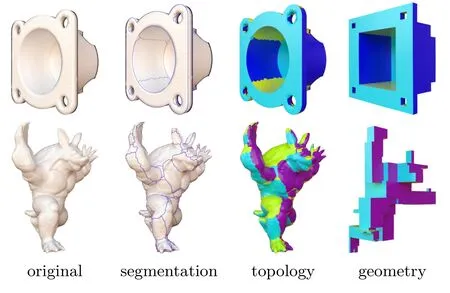
Fig.1 Segmentation,polycube topology determination,and geometry construction.

In the first step,the whole mesh is separated into several charts with monotone chart boundaries[9].Finding necessary conditions on the segmentation to guarantee a valid polycube is still an open problem[26]. However there are three sufficient conditions[26]:

a)each single patch of the polycube has at least four other neighboring charts;

b)two neighboring polycube patches must not have opposite labels;

c)the valence of every polycube vertex must be three.

In thispaper,we usethe same validated polycube topology data as Ref.[21]for purposes of experimental comparison.

In the segmentation step,we must guarantee that there are only three parts which meet at each point to satisfy the third topological requirement.The PolyCut method in Ref.[9]can be applied to perform this step.

3.2 Polycube topology

The second step determines the polycube topology.After segmentation of the mesh,this step labels or associates each triangle with one of six axis directions(+X,−X,+Y,−Y,+Z,−Z),as in Fig.1,where the six different colors represent these directions.

A valid polycube topology assigns a target normal to every triangle face,and divides the whole mesh into patches in which all triangles have the same target normal.Our algorithm rotates all triangles to their corresponding target normal directions.There are no explicit constraints between patches.Every patch is independently rotated.However there are implicit global topological constraints between them due to the polycube topology.

If the same model is assigned several different polycube topologies,this will lead to different polycube shapes.In Figs.2 and 3,we demonstrate this conclusion. The first and the third columns of Fig.2 show the same “bimba” model,but with different polycube topologies,and the second and the last columns are their corresponding polycube shapes.

3.3 Polycube geometry

3.3.1Approach

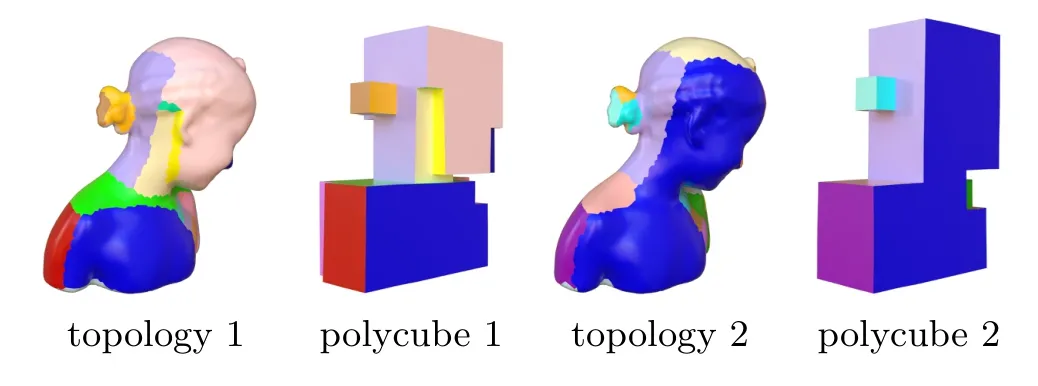
Fig.2 A model with two different polycube topologies.

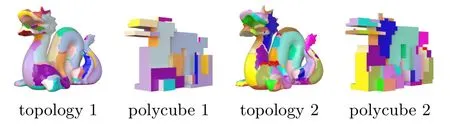
Fig.3 Another model with two different polycube topologies.

The second step aligns and reorients the triangles in each chart with one axis direction. Every chart should be mapped into a planar rectangle and all chart boundaries should be straight lines.

When creating a polycube from a mesh,we wish the parameterization distortion to be low.At the same time,the numbers of singularities,i.e.,chartcorners,and ofcharts,should be kept low. The polycube construction algorithm should provide an optimaltrade-off between parametrization distortion,and numbers of charts and singularities.

Our polycube geometry method is based on a Poisson system which reconstructs the deformed polycube mesh to satisfy the currently assigned face normals of the triangles. As the Poisson system can only approximate the input normal requirements,we use an iterative Poisson system.After several iterations,our system converges and outputs a corresponding polycube shape whose patch boundaries are necessarily straight;the triangles in each chart fall on a plane automatically without the need for any extra planarity constraints.

Changing a model into its corresponding polycube shape is fundamentally a surface deformation process. Previous deformation algorithms[27–30]focus on preserving the local features of the original model as well as possible.We suggest that the target of the deformation should be to preserve the metric instead of local features.

In Ref.[30],the deformation energy is separated into two explicit kinds of energy,stretching energy and bending energy.The former tries to preserve the metric,while the latter preserves the mean curvatures. Motivated by their explanation,our algorithm adopts and modifies their stretching energy under the constraints of the target normal direction of every triangle of the polycube topology.In their original method,the rotations of faces are unknown variables which are changed at every iterative step,but in our approach,the rotations are known in advance and kept the same in each iteration.In theory,our deformation does preserve the metric,but in practice we observe small changes in edge lengths.

3.3.2Details

LetSbe an original surface andS′be a deformed version of it,embedded in 3-dimensions.Letxvbe a 3-vector which is the position associated with vertexvofS,whilex′vcorresponds to vertexvinS′.On every triangle of the mesh,we define a 3×3 rotation matrix variableR(t).The stretching energy[30]is defined as

In the above,‖·‖2is the standard 3-vector norm,hevwrepresents the half edge from the vertexvtow.The angle of the triangle opposite to half edge hevwis denotedavw.FinallyR(tvw)represents the rotation matrix associated with the triangle face containing half edge hevw.

It is proved in Ref.[30]thatE(x′)measures the quantity:

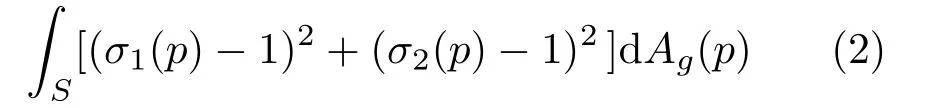
whereσ1(p)andσ2(p)represent the the maximum and minimal stretching ratios of a tangent vector ofSat a pointpunder the differential mapping dx′fromStoR3,respectively.ThereforeE(x′)is a reasonable quantity to measure the stretching of a deforming surface.

This stretching energy is quadratic inx′given a fixed rotation matrixRover each triangle.Taking the gradient of the stretching energy and setting it to zero,we can obtain the optimal values of the variablesx′by solving a single linear system:

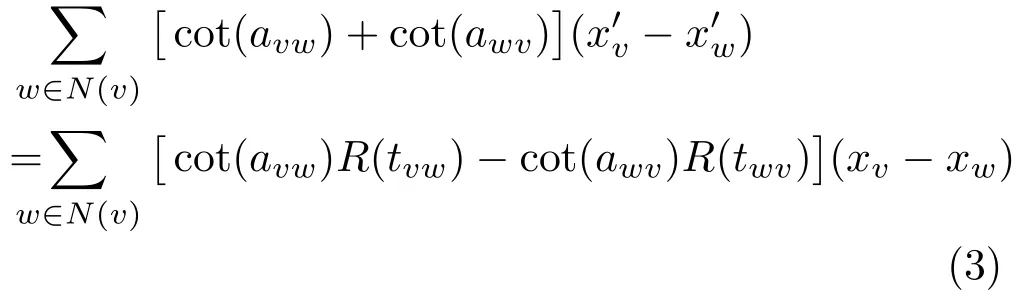
By de fi ning the 3-vector at vertexvas

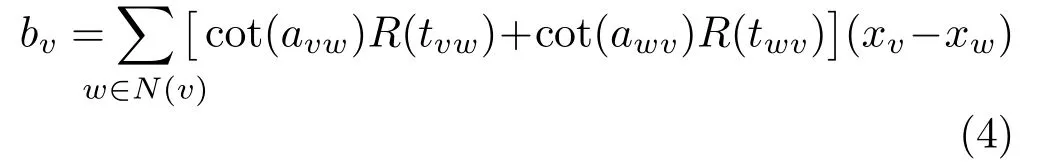
we can represent the above system in matrix format as

whereLis then×nLaplacian matrix,andx′andbaren×3 matrices.

3.3.3Rotation of each triangle

In the above system,we need to know the rotation matrix for every triangle of the mesh. Although we do not know the exact vertex positions of the polycube in advance,the face normals of the polycube are determined and fixed by the polycube topology.Therefore we can calculate the rotation matrix for every triangle,from its unit normal on the original mesh and the target normal from its polycube topology,without knowing the target polycube shape(the rotation can be computed by Rodrigues’formula).

3.3.4Iteration

A Poisson system providesan approximation method:the system in Eq.(5)cannot result in an exact polycube,of the kind shown in Fig.4.We fi x the problem with an iterative method.In every stepi,we recompute the rotation matrixRi(t)for triangletfrom the face normal of the current model and the target normal given by the polycube topology.Using the newRi(t),we update theLiandbi.On each iteration the system to be solved is

Figure 4 demonstrates the iterative process of polycube deformation.We observe that the polycube shapes get better and better after each iteration;planarity and straightness of the polycube edges are realized upon convergence of the iterations.In these experiments,the polycube shape in the fi fth step is almost the same as the one after the hundredth step.Therefore the speed of convergence of our polycube deformation method is very fast.In practice,the speed varies according to the model.

The stretching energy defined in Eq.(1)can measure the stretching ratio if it is a function of both rotationRand unknown position vectorsx′.In our framework,we fi x the variableR,so our system is only a function of unknown position vectorsx′.Therefore our method does not minimize the stretching energy,but is a simple Poisson system.The explanation of“stretching energy” in Ref.[30]gives us a hint as to why our simple Poisson system does not change edge lengths much in practice.

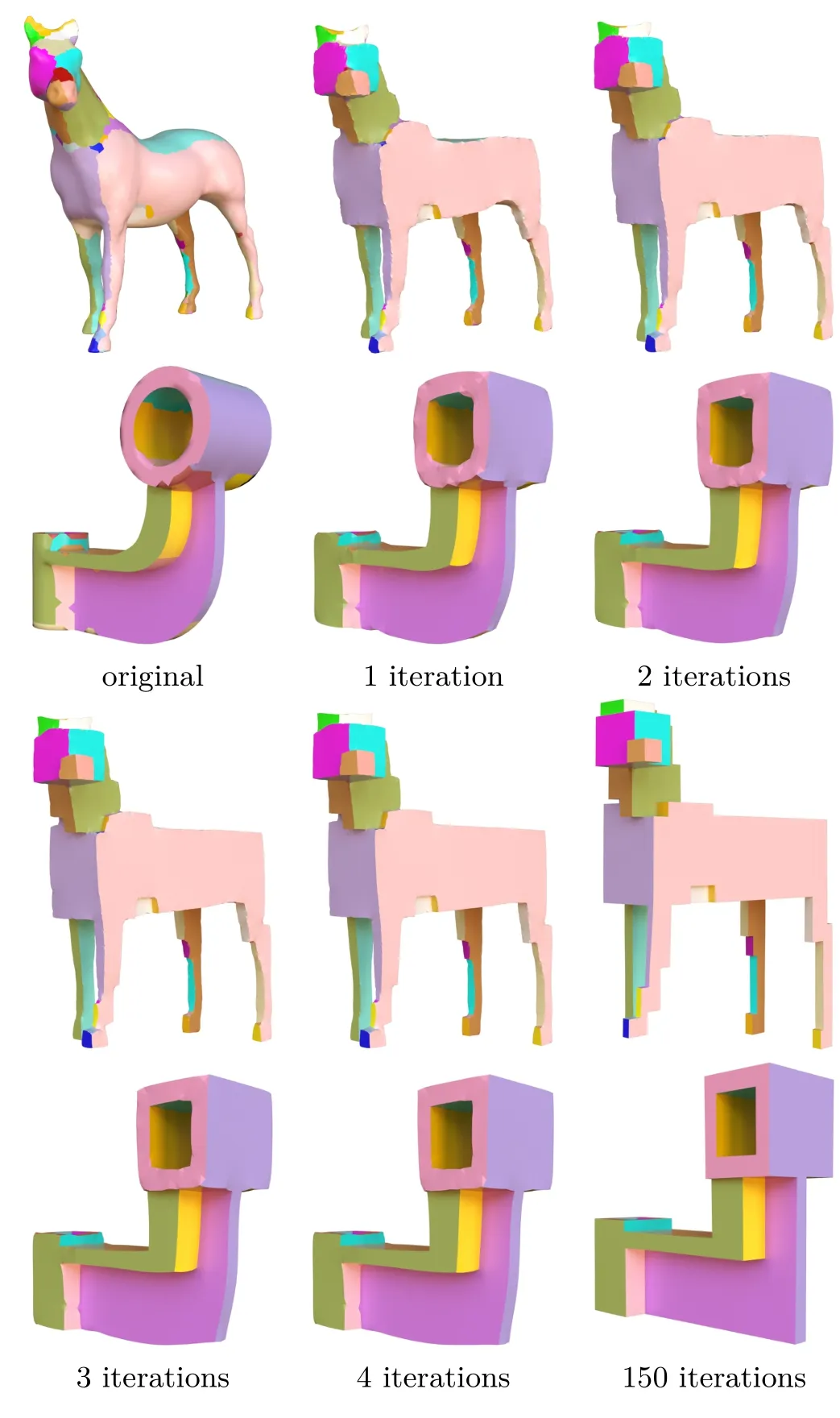
Fig.4 Iterations of polycube deformation for two models.

4 Results and demonstrations

4.1 Evaluation

Wehavetested ourmethod in avariety of meshes with complicated topology,with and without boundaries.Our experiments demonstrate that our algorithms can work on all kinds of shapes.

In Fig.5,we show several models and their polycube shapes.It shows that our algorithm can obtain perfect polycubes no matter how complex the model shapes.

Fig.5 Six models and their polycube shapes.

Polycubes are also affected by the genus of the models.The technique we propose can manipulate models with high genus directly,as shown in Figs.13 and 14,which demonstrates the robustness of our algorithm for varying mesh topologies.

Our method is insensitive to the presence of boundaries.Figure 6 shows some meshes with boundaries and their polycubes.As there are only implicit constraints on polycube topology,the edges on the boundary are not deformed into the straight lines.

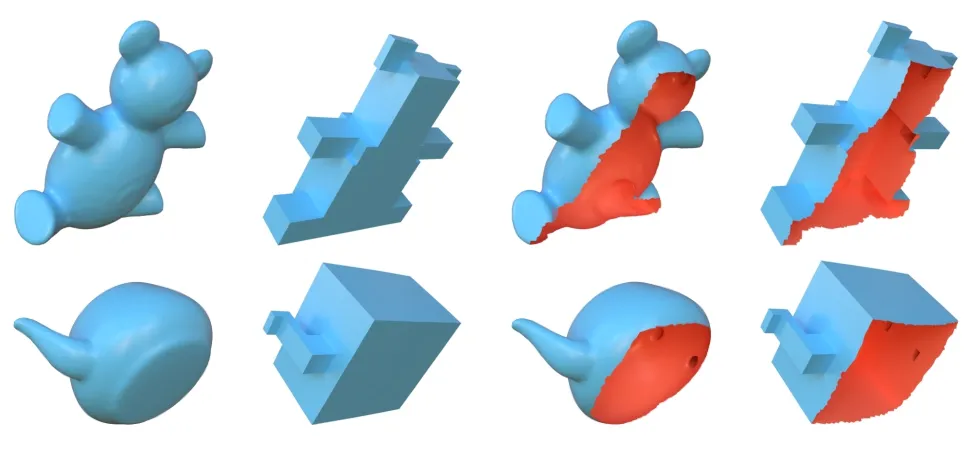
Fig.6 Models with boundaries,and their polycube shapes.

Fig.7 The “costa” non-orientable surface and its polycube.

Our algorithm can also deform non-orientable meshes successfully.In Fig.7,the well-known“costa”surface mesh is deformed into a polycube.After determining the segmentation and polycube topology,the PolyCut method[9]also uses a deformation algorithm to obtain polycube geometry.Their deformation is based on vertex normal rotations,unlike ours,in which rotations are applied to face normals.As a result,their method and the algorithm in Ref.[21]can not process non-orientable surfaces,or meshes with boundaries.

The algorithm we present is also robust to polycube topological defects.When the polycube topology is not valid,our method can still process the model and output a polycube-like shape with the same polycube topological defects.In Fig.8,two models with and without topological defects are shown in the first and third columns respectively.Corresponding polycube deformation results are displayed in the second and fourth columns.

4.2 Comparison

Fig.8 polycube topological defects. When the polycube topological defects.

Many recent algorithms[17]cannot guarantee to obtain a perfect polycube shape without topological defects,an exception being the method proposed in Ref.[21]. In this part,we compare our method with the latter. We use the same models,the same segmentation charts,and the same polycube topologies as used in Ref.[21]. We ran these algorithms on a hundred of models,and exhibit several results in Figs.9 and 10.

Our algorithm just solves several linear systems,so is faster than theirs.The polycube shapes from both algorithms are almost the same.However the area and shape of each polycube face are slightly different.

We compute the edge and area errors for each model for our and their polycube results.The error ratios for one hundred models for the two methods are displayed in Figs.11 and 12.We can conclude that our algorithm preserves edges and areas much better than the method in Ref.[21].

5 Conclusions and future work

This paper has presented a robust,efficient polycube deformation algorithm. Our method is based on explicitly separating the whole process into three steps.Each step can be performed with a variety of methods.Our method outperforms previous ones in terms of speed,robustness,simplicity,diversity,and quality.Although this deformation technique leads to a direct cross-map between original mesh and its polycube,we can not guarantee that the map is bijective,or one-to-one.In future,we plan to add further constraints to the polycube geometry step to obtain a bijective map.

Fig.9 Polycubes produced by the method in Ref.[21]and our method.

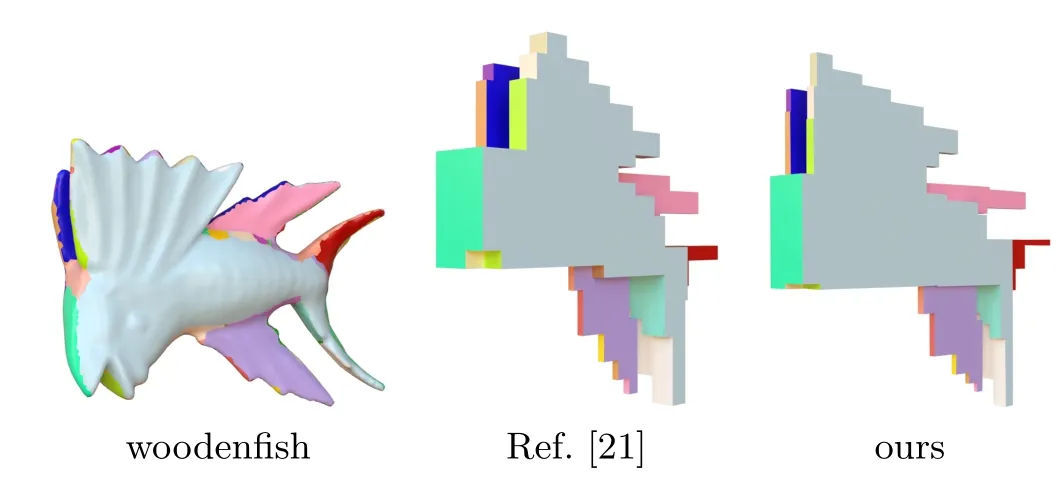
Fig.10 Polycubes produced by the method in Ref.[21]and our method.

Fig.11 Edge errors for our algorithm and the method in Ref.[21].

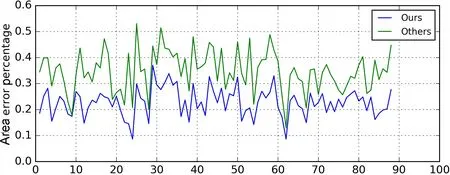
Fig.12 Area errors for our algorithm and the method in Ref.[21].

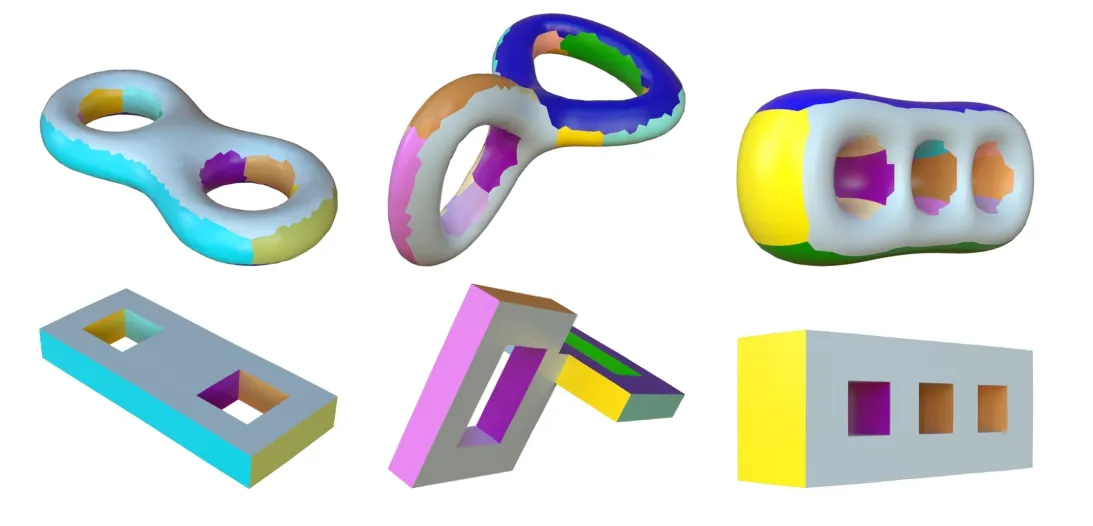
Fig.13 Models of high genus and their polycube shapes.

Fig.14 Models of high genus and their polycube shapes.

Quadrangulation and hexahedral meshing from a surface mesh are crucial problems in computer graphics,and our method shows promise for such applications.

Fig.15 Gallery of our polycube deformations.

Acknowledgements

We wish to thank the anonymous reviewers for encouragement and thoughtful suggestions.We are grateful for Prof.Steven J.Gortler for motivation and insightful guidance which made this paper possible. We also thank Yue Li for help in our experiments.The mesh models are courtesy of the Aim@Shape Repository,the Stanford 3D Scanning Repository and Ref.[21].We used Mitsuba[31]for rendering images.Our algorithms were implemented usingtheMeshDGP [32]framework.Wealso thank the Libigl team [33]for reference.The project was partially supported by NSFC 61772105,61720106005,and 11271156,NSF DMS-1418255,and AFOSR FA9550-14-1-0193.

References

[1]Tarini,M.;Hormann,K.;Cignoni,P.;Montani,C.PolyCube-maps.ACM Transactions on GraphicsVol.23,No.3,853–860,2004.

[2]Gu,X.;Gortler,S.J.;Hoppe,H.Geometry images.ACM Transactions on GraphicsVol.21,No.3,355–361,2002.

[3]Chang,C.-C.;Lin,C.-Y.Texture tiling on 3D models using automatic polycube-maps and Wang tiles.Journal of Information Science and EngineeringVol.26,No.1,291–305,2010.

[4]Garcia,I.;Xia,J.;He,Y.;Xin,S.-Q.;Patow,G.Interactive applications for sketch-based editable polycube map.IEEE Transactions on Visualization and Computer GraphicsVol.19,No.7,1158–1171,2013.

[5]Yao,C.-Y.;Lee,T.-Y.Adaptive geometry image.IEEE Transactions on Visualization and Computer GraphicsVol.14,No.4,948–960,2008.

[6]Wang,H.;Jin,M.;He,Y.;Gu,X.;Qin,H.User-controllable polycube map for manifold spline construction.In: Proceedings of the 2008 ACM Symposium on Solid and Physical Modeling,397–404,2008.

[7]Gregson,J.;Sheffer,A.;Zhang,E.All-hex mesh generation via volumetric polycube deformation.Computer Graphics ForumVol.30,No.5,1407–1416,2011.

[8]Han,S.;Xia,J.;He,Y.Hexahedral shell mesh construction via volumetric polycube map.In:Proceedings of the 14th ACM Symposium on Solid and Physical Modeling,127–136,2010.

[9]Livesu,M.; Vining,N.; Sheffer,A.; Gregson,J.;Scateni,R.PolyCut: Monotonegraph-cuts for PolyCube base-complex construction.ACM Transactions on GraphicsVol.32,No.6,Article No.171,2013.

[10]Xia,J.;He,Y.;Yin,X.;Han,S.;Gu,X.Directproduct volumetric parameterization of handlebodies via harmonic fields.In:Proceedings of the Shape Modeling International Conference,3–12,2010.

[11]Fan,Z.;Jin,X.;Feng,J.;Sun,H.Mesh morphing using polycube-based cross-parameterization.Computer Animation and Virtual WorldsVol.16,Nos.3–4,499–508,2005.

[12]Wang,H.;He,Y.;Li,X.;Gu,X.;Qin,H.Polycube splines.Computer-Aided DesignVol.40,No.6,721–733,2008.

[13]He,Y.;Yin,X.;Luo,F.;Gu,X.Harmonic volumetric parameterization using green’s functions on star shapes.In:Proceedings of the Symposium on Geometry Processing,2008.

[14]Li,X.;Guo,X.;Wang,H.;He,Y.;Gu,X.;Qin,H.Harmonic volumetric mapping for solid modeling applications.In: Proceedings of the 2007 ACM symposium on Solid and Physical Modeling,109–120,2007.

[15]Liu,L.;Zhang,Y.;Liu,Y.;Wang,W.Featurepreserving T-mesh construction using skeleton-based polycubes.Computer-Aided DesignVol.58,162–172,2015.

[16]He,Y.;Wang,H.;Fu,C.-W.;Qin,H.A divideand-conquer approach for automatic polycube map construction.Computers&GraphicsVol.33,No.3,369–380,2009.

[17]Huang,J.;Jiang,T.;Shi,Z.;Tong,Y.;Bao,H.;Desbrun,M.l1-based construction of polycube maps from complex shapes.ACM Transactions on GraphicsVol.33,No.3,Article No.25,2014.

[18]Lin,J.; Jin,X.; Fan,Z.; Wang,C.C.L.Automatic polycube-maps.In:Advances in Geometric Modeling and Processing.GMP 2008.Lecture Notes in Computer Science,Vol.4975.Chen,F.;Jttler,B.Eds.Springer,Berlin,Heidelberg,3–16,2008.

[19]Alexa,M.;Cohen-Or,D.;Levin,D.As-rigid-aspossible shape interpolation.In:Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques,157–164,2000.

[20]Wan,S.;Yin,Z.;Zhang,K.;Zhang,H.;Li,X.A topology-preserving optimization algorithm for polycube mapping.Computers&GraphicsVol.35,No.3,639–649,2011.

[21]Fu,X.-M.;Bai,C.-Y.;Liu,Y.Efficient volumetric polycube-map construction.ComputerGraphics ForumVol.35,No.7,97–106,2016.

[22]Cherchi,G.;Livesu,M.;Scateni,R.Polycube simplification for coarse layouts of surfaces and volumes.Computer Graphics ForumVol.35,No.5,11–20,2016.

[23]Yu,Y.;Zhou,K.;Xu,D.;Shi,X.;Bao,H.;Guo,B.;Shum,H.-Y.Mesh editing with poisson-based gradient field manipulation.ACM Transactions on GraphicsVol.23,No.3,644–651,2004.

[24]Xu,D.;Zhang,H.;Wang,Q.;Bao,H.Poisson shape interpolation.Graphical ModelsVol.68,No.3,268–281,2006.

[25]Zayer,R.;Rssl,C.;Karni,Z.;Seidel,H.-P.Harmonic guidance for surface deformation.Computer Graphics ForumVol.24,No.3,601–609,2005.

[26]Eppstein,D.;Mumford,E.Steinitz theorems for orthogonal polyhedra.In:Proceedings of the 26th Annual Symposium on Computational Geometry,429–438,2010.

[27]Chao,I.;Pinkall,U.;Sanan,P.;Schrder,P.A simple geometric model for elastic deformations.ACM Transactions on GraphicsVol.29,No.4,Article No.38,2010.

[28]Botsch,M.; Sorkine,O.On linearvariational surface deformation methods.IEEE Transactions on Visualization and Computer GraphicsVol.14,No.1,213–230,2008.

[29]Sorkine,O.;Alexa,M.As-rigid-as-possible surface modeling.In: Proceedings of Eurographics/ACM SIGGRAPH Symposium on Geometry Processing,109–116,2007.

[30]Zhao,H.;Gortler,S.J.A report on shape deformation with a stretching and bending energy.arXiv preprintarXiv:1603.06821,2016.

[31]Jakob,W.Mitsuba renderer.2010.Available at http://www.mitsuba-renderer.org.

[32]Zhao, H. MeshDGP: A C Sharp mesh processing framework.2016.Availableathttp://meshdgp.github.io/.

[33]Jacobson,A.;Panozzo,D.;Schller,C.libigl:A simple C++geometry processing library.2016.Available at http://libigl.github.io/libigl/.