基于Harris多摄像头孔壁图像的全景拼接技术

，，2，炳文

(1.山东科技大学 电子通信与物理学院，山东 青岛 266590；2.山东科技大学 电气与自动化工程学院，山东 青岛 266590)

我国煤炭资源分布广泛，煤矿安全生产受到国家的重视，钻孔摄像技术是当今观测分析煤矿地质结构的有效技术手段。构建钻孔全景图像可以直接有效地观测分析到钻孔内壁的地质结构信息。目前构建孔壁全景图像的方法主要有折反射镜全景成像或全景环形透镜、旋转单个摄像机拍摄系统、鱼眼镜头拍摄。2001年，漆驰等[1]提出运用相邻图像拼接的方法获取全景图，采用普通摄像机旋转拍摄多幅图像，然后根据相邻图像之间的重叠区域，实现图形配准获取全景图。但是摄像机旋转的过程中容易造成“鬼影”现象，同时也无法满足拼接的实时性。目前常用的方法是王川婴等[2]在2002年提出的数字式全景钻孔摄像，采用截头的锥面反射镜，利用光学原理，将钻孔孔壁图像反射成为平面图像。但是现有的构建孔壁全景图像的方法中存在着图像边缘空间分辨率低、图像采集设备价格昂贵、图像畸变等问题。

为实时获取高分辨率的孔壁全景图，并消除旋转相机带来的“鬼影”现象，本研究采用四个115°广角镜头水平环绕放置拍摄孔壁图像实现全景拼接的系统[3]，由于采用广角镜头成像设备以及孔壁曲率等因素的影响，拍摄的图像出现几何畸变现象[4]。本课题共同研究者张炳文提出“两步法”矫正方案，采用手动调整径向参数消除广角镜头引起的光学畸变，然后建立非均匀插值模型恢复曲率影响的图像信息。但经过这种手动调整参数和非均匀插值模型，得到的图像精确度降低，增加了图像拼接的误差。因此，针对孔壁图像受孔壁曲率影响的特殊性，本研究提出基于参数微调的畸变图像校正算法，自动调节畸变参数；采用柱面信息还原法解决孔壁曲率对图像信息的影响，利用Harris角点检测算法进行匹配拼接，能够满足视频拼接实时性的要求。

1 图像畸变矫正

1.1 畸变模型的建立

由于本研究所采用的摄像机是广角镜头。获取的图像存在着广角镜头引起的光学畸变，在图像拼接时,需要对广角相机产生的畸变进行消除。引起畸变的因素主要包括镜头的径向畸变、采集畸变以及偏心畸变等[5]。对非线性畸变建立数学校正模型[6-8]：

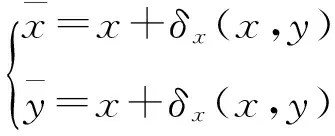
(1)

(2)

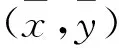
对于钻孔场合，径向几何畸变产生的影响最大。径向畸变的数学模型可以简化为：

(3)

由式(3)可以看出，理想图像与畸变图像之间的关系由参数k1、k2确定，从而根据该模型将所拍摄图像进行畸变矫正。

1.2 摄像机标定

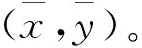
本研究提出基于参数微调的畸变图像校正算法，即在相机标定得到畸变参数的基础上，进行参数微调，以达到图像准确校正的效果。由于相机标定的畸变参数离最优值不会太大，因此参数调整应该在相机标定畸变参数初始值附近微调，算法具体步骤为：

1) 利用OpenCV对平面网格模板进行摄像机标定，求出径向畸变参数。

2) 以k1、k2为初始畸变参数，进行畸变校正。将校正的图像进行边缘增强、二值化、中值滤波和细化等图像处理后获取模板上的网格交点坐标。

3) 利用斜率判断校正效果，令α=(yi-yi-1)/(xi-xi-1)，β=(uyi+1-yi)/(xi+1-xi)，e=2(α-β)/(α+β) ，设定斜率阈值为0.03。若e<0.03，则说明畸变校正效果良好，畸变参数无需进行优化调整。否则，按步骤4)进行畸变参数的优化调整。

4) 以步长d1=k1/50,b1=k2/50为初始步长，调整畸变参数k1、k2，使k1=k1±d1，k2=k2±b1，并判断是否满足e<0.03。若不满足则进行步骤5)。

5) 令dj+1=(j+1)d1,bj+1=(j+1)b1,j为搜索的次数,初始值j=1。调整步长，执行步骤4)，直至满足e<0.03为止。

由于初始畸变参数本身就已经接近最优点，并且经过多次试验，在初始点附近搜索10次左右，就会找到满足的值，因此，该方法有效。

利用上述方法进行畸变参数的调整，可以将所拍摄柱形曲面图像校正，也是对平面网格模板法的一种改进，矫正结果如图3所示。

图1 孔壁内采集图像Fig.1 Collected images inside the borehole

图2 网格模板法校正后的图像Fig.2 Corrected image with the plane gridding model

图3 参数微调算法校正图像Fig.3 Corrected image with parameter adjustment

1.3 柱面信息还原法展开图像

从图3中可以看出，光学畸变明显得到矫正，但是由钻孔内侧曲率造成的图像信息损失得不到恢复，左右两侧网格宽度明显小于中间网格宽度。本研究背景为钻孔图像，每个摄像头所采集图像为经过图像信息压缩的孔壁图像的弦面，并且越靠近左右边缘图像压缩越严重。模拟钻孔环境图像采集模型如图4所示：

为了恢复图像信息，计算拍摄平面I与实际钻孔面J的对应坐标关系，设P(x,y)为I上一像素点，Q(x′，y′)为P点在J上的对应点。P点在相机坐标系下的坐标为(x-W/2,y-H/2,-f)，坐标系原点与象素点P连线的直线参数方程为：

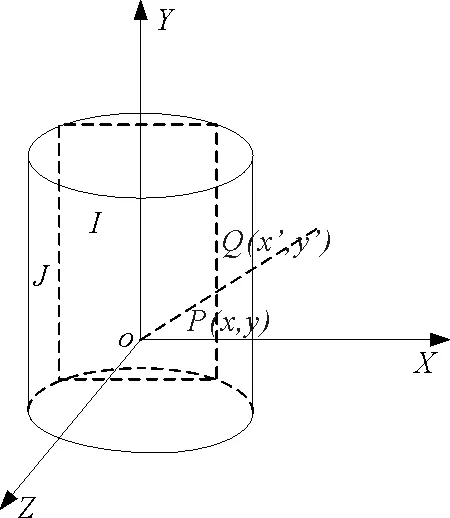
图4 采集图像与孔壁图像关系图Fig.4 The relationship between collected images and borehole images

(4)

其中,t为参数。圆柱面的方程可以表示为：

u2+v2=f2。

(5)

联立式(4)和(5)得到的即为直线OP与圆柱面J的交点Q。

需要把三维的参数坐标转变为二维的图像坐标才便于存储，变换公式为：

(6)

联立(4)、(5)、(6)式得到P(x,y),Q(x′，y′)的坐标关系式：

(7)

图5 柱面信息还原法展开图像Fig.5 The expanded image using the cylindrical information reduction method

式中：f为相机焦距，W、H分别为所拍摄图片的宽度和高度。在图像采集过程中，在纵向上不发生变形，因此令y′=y。遍历原图像像素点(x,y)，根据式(7)，即可还原由圆柱内侧曲率引起的图像信息缺失。在图像变换的过程中,采用双线性插值法对图像灰度信息进行调整。在图3的基础上，经过本算法调整后的图像如图5所示。

2 基于Harris角点检测算法的图像拼接

图像拼接技术在图像处理方面得到广泛的应用。图像拼接技术包含三个方面：角点提取、图像配准和图像融合。提出了一种基于Harris角点检测的图像拼接算法，利用Harris算法提取角点、SSD算法配准图像、RANSAC算法提纯匹配对，渐入渐出的融合算法完成对两幅图像无缝拼接。

2.1 Harris角点提取和基于SSD 的配准

Harris 角点检测基于Moravec角点检测算法，利用微分运算、高斯平滑提取角点。其中，微分算子体现了图像的灰度变化，通过这些变化能够有效分辨边界和角点，另一方面微分算子具有两个优势：旋转不变、仿射不变，这种优势能够增加其检测范围。高斯平滑能够降低噪声提取角点时的影响。

角点检测响应函数由C.Harris首次提出，公式如下：

R=det(M)-k*Trace2(M)。

(8)

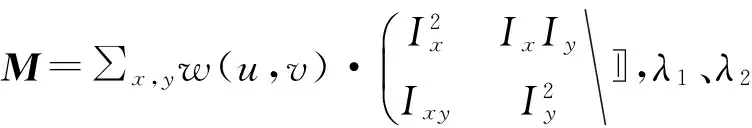
算法如下:

1) 在图像的像素点上，分别计算在和方向上的一阶导数Ix、Iy，以及Ixy。

2) 对Ix、Iy、Ixy高斯平滑。

3) 根据式(8)计算各像素的R值。

4) 角点判断：设定阈值t，当R>t时，为角点，否则不是角点[13]。

Harris 特征检测得到的角点，角点的特征匹配可通过基于像素差平方和SSD的图像配准算法进行运算。通过两图像之间的灰度值来实现特征点的匹配。将图像分块处理，依次根据公式(9)计算，且值最小的块上的特征点，就是匹配点。

SSD=∑x,y∈w[I1(x,y)-I2(x,y)]2。

(9)

2.2 RANSAC算法计算变换矩阵

RANSAC算法由Fischler和Bolles提出，可以有效剔除匹配外点，同时计算过程简单、具有较强的容错能力，增大图像配准的精确度[14]。通过迭代方法，反复选择坐标点数据进行计算，筛选掉不合适的数据。

在透视变换模型中，首先以一幅图像作为参考图像，另一幅图像为待拼接图像，通过匹配点之间的对应关系，计算出变换矩阵，就可实现图像的拼接过程，变换模型为：

(10)

式中，H为投影变换矩阵，(x2,y2)为图像I2对应匹配点的像素坐标。

在图像拼接的理论计算中，可以通过4组相匹配的特征点计算出单应阵H。实际计算时，一般要提取20对以上的匹配点对，求出的H值才会比较准确。

2.3 图像融合

经过透视变换后，就可以得到图像之间的重合部分，并对重合部分进行图像融合，消除图像拼接的接缝。本文采用融合速度较快的渐入渐出融合算法。算法实现过程为：在进入到融合区之前，I1的权重系数一直保持为 1，I2的权重系数为0；进入到过渡带之后，I1的系数逐渐递减至0，I2的系数逐渐递减至0。

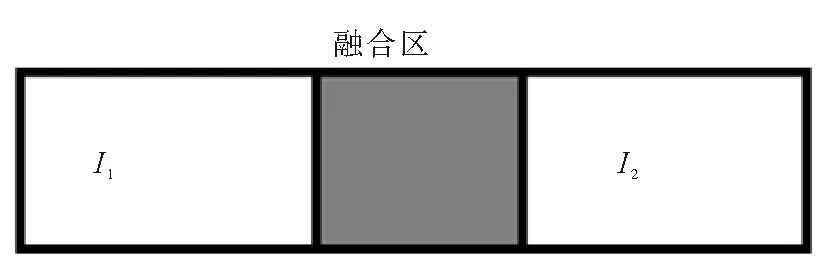
图6 图像融合示意图Fig.6 Image fusion

其渐变系数β可由图像I1和I2的水平重叠距离求得。设两幅图像的灰度值为I1(x,y)和I2(x,y)，则重叠区域图像的灰度值为

I(x,y)=βI1(x,y)+(1-β)I2(x,y)。

(11)

当β由 1 逐渐变化到 0 时，图像从I1(x,y)逐渐过渡到I2(x,y)，从而实现了图像间的平滑过渡、无缝拼接。

3 实验结果及分析

实验用4个115°广角镜头采集实验图像进行仿真模拟，使用的计算机参数配置为：Windows 7操作系统， CORE i5处理器，RAM 2G。同时使用软件平台为MATLAB 2013a版本，部分参数的验证用到软件Visual Studio 2010和OpenCV2.4.9库。通过视频采集卡的图像大小均为像素。图7(a)为镜头采集的孔壁图像。经过畸变校正、曲率影响的图像信息恢复后得图7(b)，使图像信息更加真实可靠。拼接算法采用Harris角点检测算法提取角点并进行初步匹配，然后经过RANSAC算法剔除外点，最后利用渐入渐出的融合算法消除拼接痕迹，得到孔壁全景图图7(c)。

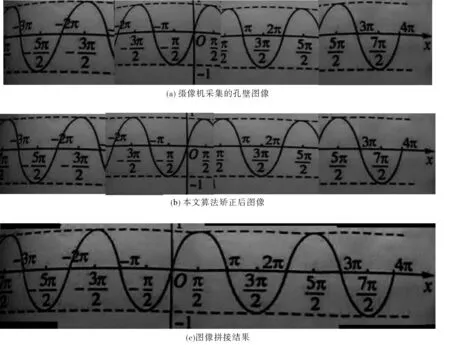
图7 实验结果Fig.7 Experimental results

本算法考虑了钻孔孔壁图像曲率对图像采集的影响，将图像矫正算法分成三步完成，使矫正图像信息更加真实可靠。同时，特征点匹配过程中，每两幅图直接平均初始配准有159对匹配对，并存在很多误匹配点对，经过RANSAC算法剔除外点后剩余42对匹配对。图像拼接算法运算时间平均用时为42.3 ms。

从图像拼接的匹配率和准确性两方面进行评价，图像拼接的匹配率定义为：

图像拼接的准确性用坐标的均方根误差表示，计算待匹配图像透视变换后的特征点与匹配图像相应特征点之间分别在方向上的均方根误差RMSE(root-mean-square deviation)，如表1所示。

表1拼接算法的匹配率与准确性
Tab.1 Match rate and accuracy

拼接方法平均匹配率/%RMSExRMSEy直接拼接本文矫正后拼接45.267.10.630.170.250.12

经过比较，本图像矫正算法提高了图像的匹配率，降低了特征点配准的均方根误差，提高了钻孔图像拼接全景图的准确率和观察效果。

4 结论

本研究针对钻孔特殊环境，采用多摄像头系统同步采集孔壁图像实现全景拼接，提出了改进的图像畸变校正方法。提出的基于参数微调的畸变图像校正算法和柱面信息还原法，通过图像拼接实验结果表明,该算法能够有效矫正图像畸变，恢复钻孔图像边缘压缩信息。提高了特征点之间的匹配率与准确性，最终获得了精确的拼接效果。同时通过本实验视频采集系统进行视频拼接时，图像变换矩阵H只需求取一次 ，规避了每帧图像都要计算透视变换矩阵的计算量，为后续的视频拼接奠定了良好的基础。本算法有效地运用在孔壁图像中，实现钻孔孔壁图像的全景拼接。

参考文献：

[1]漆驰,刘强,孙家广.摄像机图像序列的全景图拼接[J].计算机辅助设计与图形学学报,2001,13(7):605-609.

QI Chi,LIU Qiang,SUN Jiaguang.Video mosaic for panoramic image[J].Journal of Computer-Aided Design and Computer Graphics,2011,13(7):605-609.

[2]王川婴,葛修润,白世伟.数字式全景钻孔摄像系统研究[J] .岩石力学和工程学报,2002,21(3):398-403.

WANG Chuangying,GE Xiurun,BAI Shiwei.Study on the digital panorama borehole camera system[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(3):398-403.

[3]曹茂永，赵猛，滕升华，等.4路钻孔孔壁视频的柱面全景图生成方法及装置：CN106023066A [P].2016-10-12.

[4]牛建军,刘上乾,姚荣辉,等.高准确度光电成像测量系统图像畸变校正算法[J].光子学报,2006,35(9):1317-1320.

NIU Jianjun,LIU Shangqian,YAO Ronghui,et al.Algorithm for image correction in high precision imaging measurement system[J].Acta Photonica Sinica,2006,35(9):1317-1320.

[5]郑佳,李学鹏.全景系统中大视场摄像机径向畸变校正算法研究[J].光学与光电技术,2016,14(3):87-94.

ZHENG Jia,LI Xuepeng.Research on radial distortion correction algorithm for camera with large field of view in panoramic system[J].Optics & Optoelectronic Technology,2016,14(3):87-94.

[6]VON GIOI R G,MONASSE P,MORELJ M,et al.Lens distortion correction with a calibration harp[C]// IEEE International Conference on Image Processing.IEEE,2011:617-620.

[7]杨必武，郭晓松.摄像机镜头非线性畸变矫正方法综述[J].中国图象图形学报，2005,10(3):269-274.

YANG Biwu,GUO Xiaosong.Overview of nonlinear distortion correction of camera lens[J].Journal of Image and Graphics,2005,10(3):269-274.

[8]TRECKEL B,EVERS-SENNE J F,KOCH R.Lens model selection for a markerless AR tracking system[C]// Proceedings of the International Symposium on Mixed and Augmented Reality.IEEE Computer Society,2005:130-133.

[9]蔡睿.基于DSP的数字图像畸变校正技术研究[D].武汉：华中科技大学，2006．

[10]朱铮涛,黎绍发,陈华平.基于平面网格模型的摄像机镜头畸变校正技术[J].计算机工程与应用,2004,40(23):32-35.

ZHU Zhengtao,LI Shaofa,CHEN Huaping.Technology of proofreading the camera lens distortion based on the plane gridding model[J].Computer Engineering and Applications,2004,40(23):32-35.

[11]TSAI R Y.A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-the-shelf TV camerasand lenses[J].IEEE Journal on Automation,1987,3(4):323-344．

[12]ZHANG Z Y.A flexible new technique for camera calibration[J].Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

[13]赵小川.现代数字图像处理技术提高及应用案例详解(MATLAB版)[M].北京:北京航空航天大学出版社，2012.

[14]苗彩霞,纪筱鹏.基于Hough变换及SIFT特征提取的图像匹配方法[J].山东科技大学学报(自然科学版),2014,33(4):105-110.

MIAO Caixia,JI Xiaopeng.An image matching algorithm based on Hough transform and SIFT[J].Journal of Shandong University of Science and Technology (Natural Science),2014,33(4):105-110.