考虑行波效应的某大跨桥梁地震响应分析

， ，

(1.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590; 2.青岛理工大学 工程质量检测鉴定中心，山东 青岛 266033)

大量地震记录表明，地震时地表各处的振动不同，即使相距仅几十米，振动的幅值、相位与频谱特征也不尽相同[1]。由于地震地面运动是一复杂的时间-空间过程，地震波在其传播过程中具有的行波效应、局部场地效应和部分相干效应等使其传到地表的各点地面振动不完全相同，使结构反应变得复杂[2,3]。随着结构跨度的增大，地震动的变异对结构的影响不可忽视。已有研究表明:对于大跨度空间结构，地震动的行波效应影响显著[4-6]。因此，在对大跨度空间结构进行抗震分析时应考虑地震动的行波效应。闫晓宇等[7]通过地震模拟振动台阵试验，对一致激励、行波激励和局部场地效应等对刚构桥地震响应进行了研究，结果表明，行波效应对该大跨刚构连续桥梁的无控制地震反应、半主动控制地震反应和减震效果均有显著影响。魏凯等[8]利用绝对位移法计算了多联长跨组合结构桥在多种行波激励工况下的地震响应，研究了激励输入模式、视波速、行波输入方向等因素对组合结构桥梁地震响应的影响规律。闫斌等[9]建立了考虑地震动行波效应的简支梁桥梁轨相互作用模型，分析了行波效应作用下轨道结构对桥梁地震响应的影响，研究了行波效应下钢轨和墩台的受力特性，并对相关参数的影响做了探讨。行波效应对大跨度桥梁结构振动反应的影响与地震波特性、波速、结构特性等诸多因素相关，对结构不同位置构件的影响程度亦不尽相同，在该方面还需进一步探索。

1 结构模型

某铁路、公路两用桥梁，是三跨连续钢桁梁，各跨均为160 m。主桁为平弦菱形桁，节间距8 m，桁高16 m，下加劲桁弦高14 m；两主桁架中心距为14 m。主桁及铁路横梁等主要结构用Q345低合金钢或性能相似的桥梁钢。全桥除铁路纵桁梁连接采用高强度螺栓和公路采用焊接纵梁外，钢梁基本为铆接结构。铁路桥面采用明桥面，铺设焊接长钢轨。右端桥墩上设固定支座，其余3个桥墩上设辘轴活动支座。墩帽及墩身均为圆端型实体结构[10]。

该桥各主要构件材料特性：连续钢桁梁钢材弹性模量为2.1×105MPa，泊松比为0.28，密度为7.85×103kg/m3；公路桥面用轻质混凝土，密度为2.0×103kg/m3。

采用ANSYS软件建立该连续钢桁梁桥有限元模型时，单元选取如下：主桁杆件、铁路纵梁、横梁、上下平横向连接系等采用三维梁单元BEAM4模拟，公路纵梁、公路桥面混凝土以及铁路混凝土轨枕、无缝钢轨等对结构刚度贡献较小的部分简化为质量单元MASS21，质量单元加在上、下平联的相关节点上。所建立的有限元模型共有7 960个单元，5 227个节点，如图1所示。

图1 桥梁有限元模型Fig.1 Bridge finite element model

2 模态分析

通过模态分析可以得到结构的动力特性，了解结构的整体性。采用Block Lanczos方法提取了前20阶模态，其中前10阶振型的自振频率、周期如表1所示。

表1 结构整体模态Tab.1 Structural modes

结构前两阶振型如图2所示。该结构的基本自振周期为1.083 s。结构的前四阶振型以平动为主，第5至7阶振型以竖向振型为主，其他振型以局部振动为主，结构整体性良好。

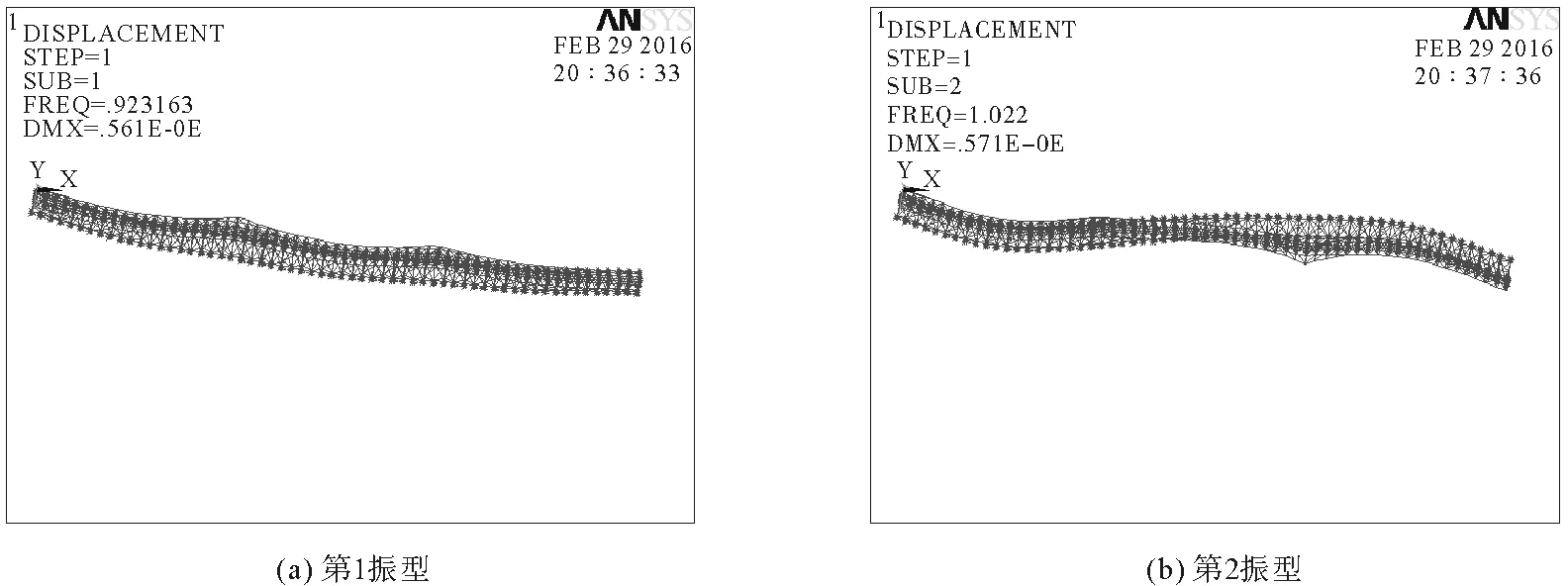
图2 桥梁振型图Fig.2 Mode shapes of the bridge

3 地震作用时程分析

3.1 地震波的输入

本结构所处地区抗震设防烈度为7度(0.15g)，二类场地，对应罕遇烈度地震加速度峰值取310 cm/s2。选用El-Centro波(1940NS)、Taft波(1952N21E)和Imperial Valley波(1979S40E，简称Imp波)作为地震激励，时间步长均为0.02 s，时长分别为：53.72、54.32和39.12 s。采用基底输入位移波激励的方法，对结构施加地震作用。根据加速度时程二次积分得到位移时程曲线，再对二次积分导致位移时程的零线漂移进行校正。采用FFT方法滤去低频分量进行校正，将滤波后得到的位移波按加速度峰值缩放比例进行调整。

桥梁在四个桥墩顶点处为固定约束，分析共考虑4种工况：①一致地震激励，采用纵向(X向)多点一致输入地震波；②行波激励，采用纵向多点非一致输入，地震波速取300 m/s；③行波激励，采用纵向多点非一致输入的方法，地震波速取600 m/s；④行波激励，采用纵向多点非一致输入，纵向地震波速取900 m/s。

3.2 结构阻尼模型

桥梁结构地震作用时程分析时，结构的阻尼采用瑞雷阻尼模型，通过前述结构模态分析结果，取以纵向振动为主的前两阶模态频率分别为4.703和8.627 Hz，结构阻尼比取为0.03，计算得到瑞雷阻尼系数α=1.147 5，β=0.000 7。

3.3 一致激励与非一致激励地震响应分析

地震波沿桥纵向由左向右传播，各点相对位移为上部结构绝对位移反应与1号桥墩激励位移的相对值。在三条波激励下，各跨跨中分别在工况1与工况2时的纵向相对地面振动位移反应的最大值如表2所示。图3(a)是工况1的节点坐标-位移峰值对应图，可以看出，一致激励下，桥梁的各跨杆件水平向位移差异较小。Imp波引起的结构位移响应相对于El-Centro波和Imp波要大；三条波分别激励时72号节点位移相对于92和114号节点为最大，因72号节点位于桥梁的左边跨， 92号节点位于桥梁的中间跨，114号节点位于桥梁的右边跨，说明桥梁的左边跨相对于中间跨和右边跨而言位移较大，但其绝对值并不大。图3(b)是工况2的节点坐标-位移峰值对应图，可以看出，考虑行波效应时对各跨位移反应均有影响，行波激励时左边跨至右边跨的位移是逐渐增大的，右边跨位移最大，三条波分别激励时Imp波引起的位移响应最大，与一致激励时结论一致。

桥梁共有4个桥墩，由左至右分别是1号、2号、3号、4号桥墩，工况1与工况2时各桥墩基底剪力计算结果如表3所示，表中数值为绝对值较大值。从表3可以看出，考虑行波效应时，各桥墩处的水平剪力均有显著增大。一致激励时，2号桥墩基底剪力值相较与其他三个桥墩为最大，1号桥墩基底剪力为最小。行波激励时各桥墩基底剪力值之间相差不大，4号桥墩基底剪力值比其他三个略微大。行波效应对桥墩剪力影响显著。

表2 节点相对位移峰值Tab.2 Peak relative displacement of the node mm

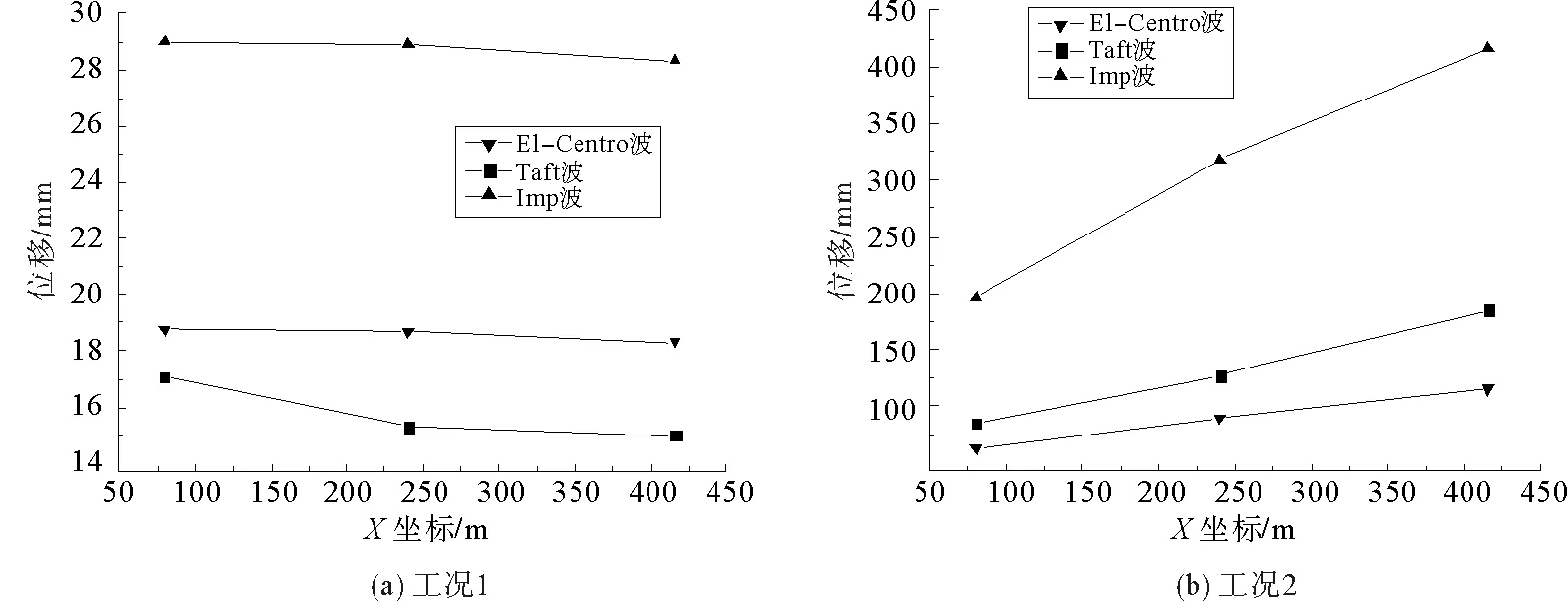
图3 节点坐标-位移峰值图Fig.3 Peak values of nodal displacement

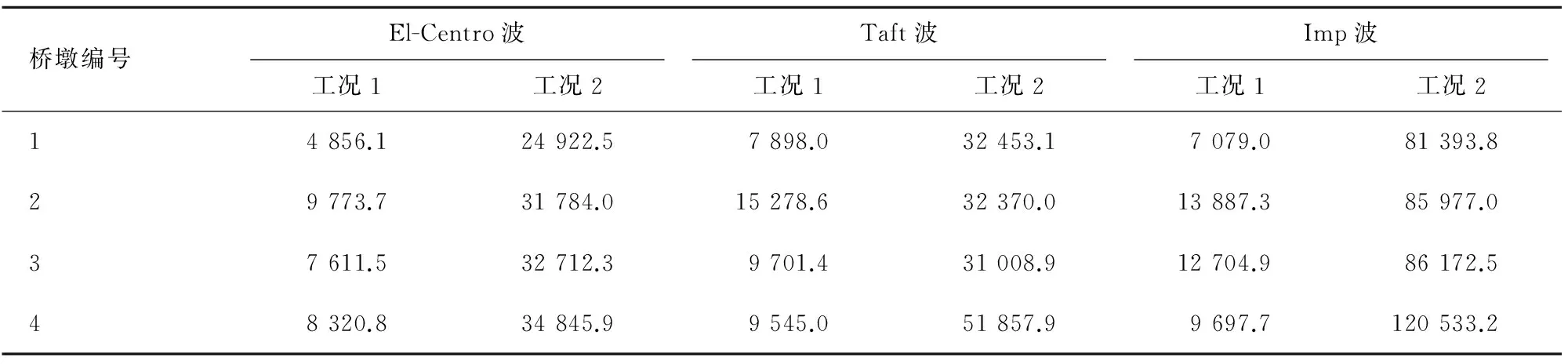
kN

墩底处杆件是结构设计的主要控制杆件，将桥墩处杆件分为五组，分别是左边跨左墩处和右墩处杆件、中间跨左墩处和右墩处杆件以及右边跨左墩处杆件，从这五个部位选择最靠近支撑点的杆件进行研究，上部杆件则从每跨取2根斜杆进行研究。工况1与工况2时部分杆件应力最大值如表4所示，表中数值为绝对值较大值。

由表4可知，工况2与工况1下相比较，桥墩上部附近杆件内力均有所增大，跨中处杆件内力变化则较小。

不同地震波激励下，杆件内力反应亦不尽相同。工况1时，上部杆件在Taft波激励下应力最大，在El-Centro波激励下应力最小；桥墩处斜向杆件应力明显小于上部杆件和桥墩处平行杆件应力；上部杆件中左边跨杆件比中间跨和右边跨杆件应力大；斜向杆件中右边跨左墩处的杆件应力比其他部位的应力大。工况2时，桥墩处斜向杆件应力明显小于上部杆件和桥墩处平行杆件应力，三条波激励下斜向杆件应力相差不大；上部杆件中左边跨和中间跨杆件比右边跨杆件应力大；平行杆件中左边跨左墩处杆件应力比其他4个部位杆件应力大，其他四个部位杆件内力则相差不大；斜向杆件中右边跨左墩处的杆件应力比其他部位杆件应力大。

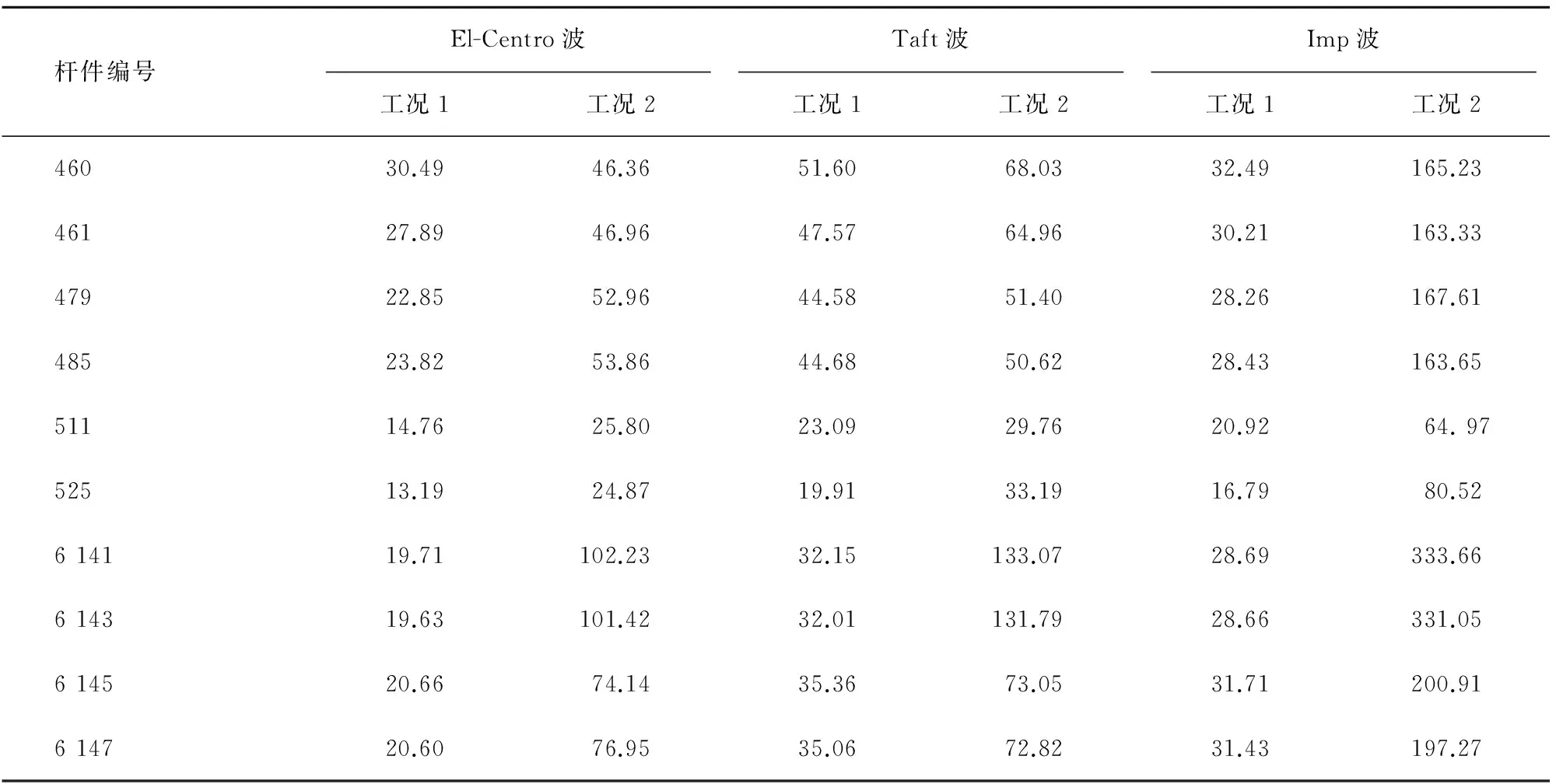
表4 部分杆件应力Tab.4 Stress of members MPa

3.4 行波速度的影响

考虑波速分别为600和900 m/s时行波对结构地震反应的影响，工况3与工况4时节点纵向相对位移反应的最大值如表5所示，表中数值为绝对值较大值。

表5 行波激励节点相对位移Tab.5 Relative displacement of nodes under traveling wave excitation mm

在不同地震波激励下，结构反应不同，Imp波引起的结构位移响应最大，Taft波次之，El-Centro波最小。随着波速增加，同一节点的相对位移减小。

工况3与工况4时各桥墩基底剪力计算结果如表6所示，表中数值为绝对值较大值。

在三条波分别激励下，Taft波引起的各桥墩基底剪力最小，Imp波和El-Centro波引起的各桥墩基底剪力均较大。2号和3号桥墩基底剪力小于1号和4号桥墩基底剪力，设计时应着重注意1号、4号桥墩。地震波速对结构反应有一定影响，随着波速从600增大到900 m/s，各桥墩剪力均有所减小。

工况3与工况4时部分杆件应力最大值如表7所示，表中数值为绝对值较大值。

在三条波分别激励下，Imp波引起的桥墩处杆件应力最大，El-Centro波次之，Taft波最小；考虑波速时，随着波速增大杆件应力减小。桥墩处平行杆件内力最大，上部跨中杆件次之，桥墩处斜向杆件内力最小，明显小于桥墩处平行杆件和上部跨中杆件。

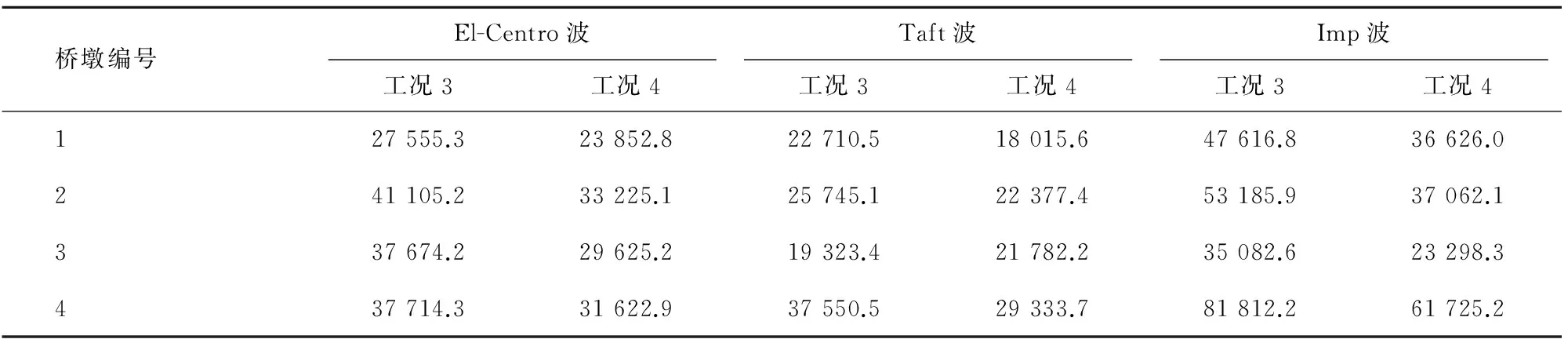
表6 行波激励桥墩基底剪力Tab.6 Bridge base shear under traveling wave excitation kN

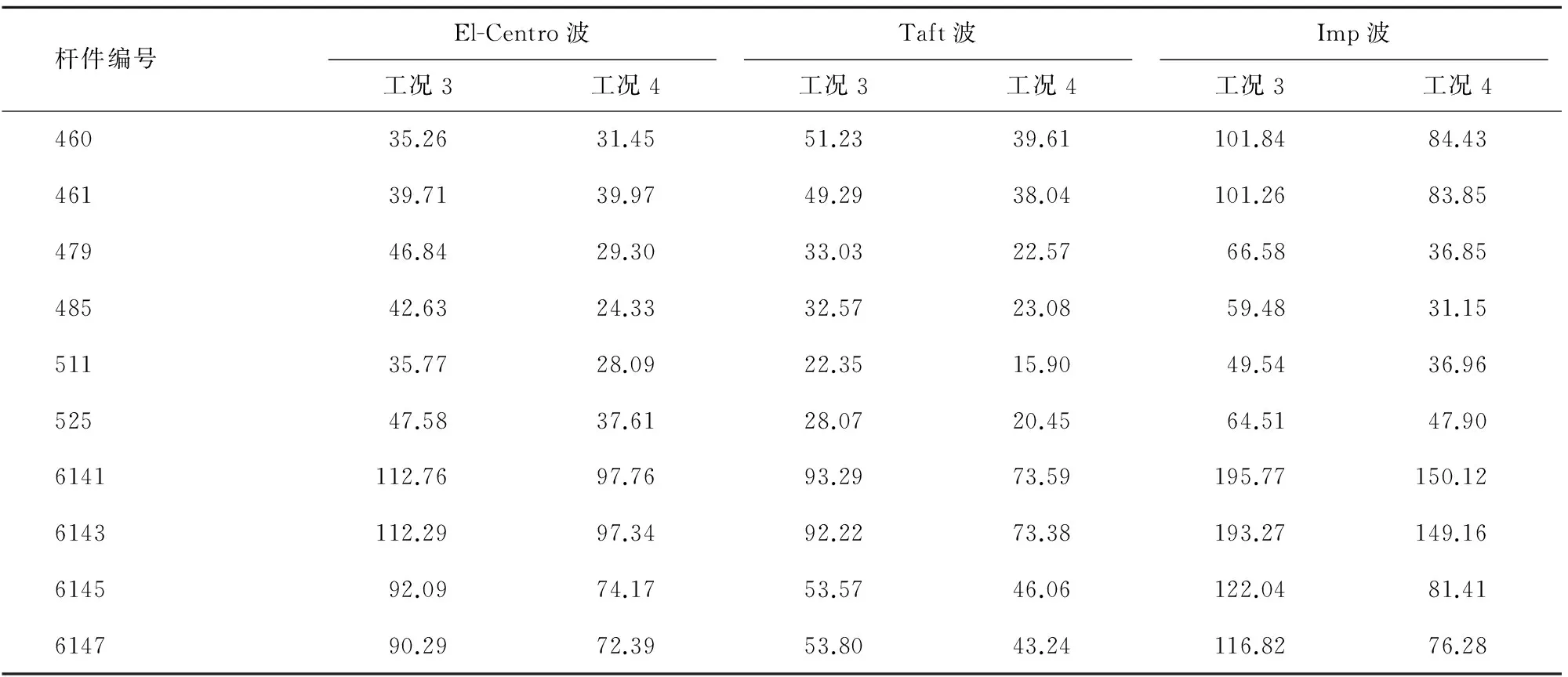
表7 行波激励部分杆件应力Tab.7 Stress of members under traveling wave excitation MPa

3.5 行波激励与一致激励对比分析

在研究行波激励对结构响应影响和变化规律中，一般定义行波效应影响系数γ为非一致激励下构件响应的峰值与一致激励下同一构件对应响应峰值的比值。

三种工况下节点位移的行波效应影响系数如表8所示。

表8 节点位移的影响系数Tab.8 Effect coefficient of nodal displacement

图4是三节点的行波效应影响系数与坐标的对应关系图。由表8和图4可以看出，考虑行波效应使节点位移增大，均大于一致激励时的节点位移，但随着波速增大位移呈减小趋势；三跨中右边跨行波影响最大，由左至右行波影响越来越大；三条波中Imp波行波效应最明显。

三种工况下各桥墩的基底剪力行波效应影响系数如表9所示。可以看出，考虑行波效应使各桥墩基底剪力增大，均大于一致激励时的基底剪力值，行波效应影响系数最大值为12.43，所以大跨度桥梁设计时应考虑行波效应的影响，尤其应注意低波速的影响。

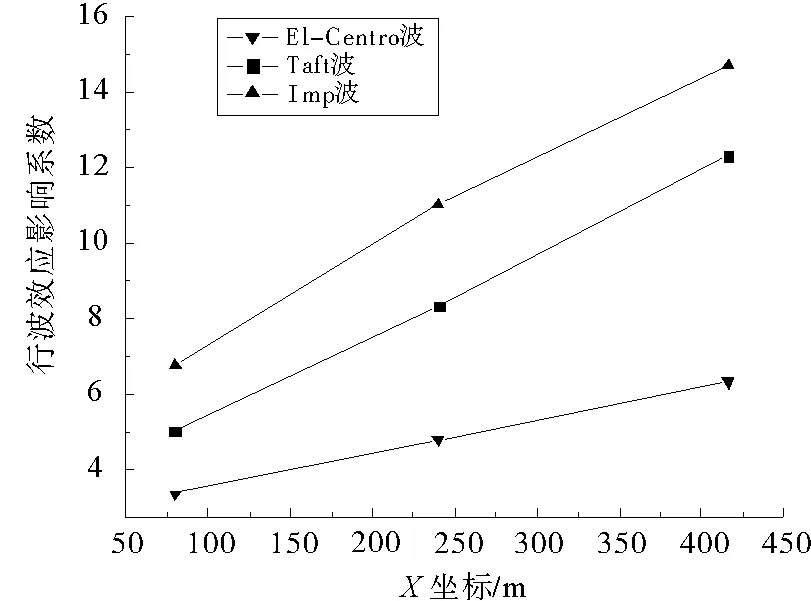
图4 节点位移的影响系数Fig.4 Effect coefficient of nodal displacement

三种工况下部分杆件应力行波效应影响系数如表10所示。可以看出，上部杆件应力有的比一致激励时的应力大，有的则小，桥墩处杆件应力均比一致激励时的应力大；上部杆件受行波效应的影响程度明显小于桥墩处杆件受行波效应的影响程度；桥墩处平行杆件的应力明显大于斜向杆件的应力，但斜向杆件内力增大程度却是最严重的，其行波效应影响系数明显大于桥墩处平行杆件和上部跨中杆件的影响系数；因此设计斜向杆件时需要留有更大的设计储备；桥墩处平行杆件和斜向杆件受行波效应影响都较大的部位是中间跨右墩处。

表9 各桥墩基底剪力的影响系数Tab.9 Effect coefficient of base shear of each pier

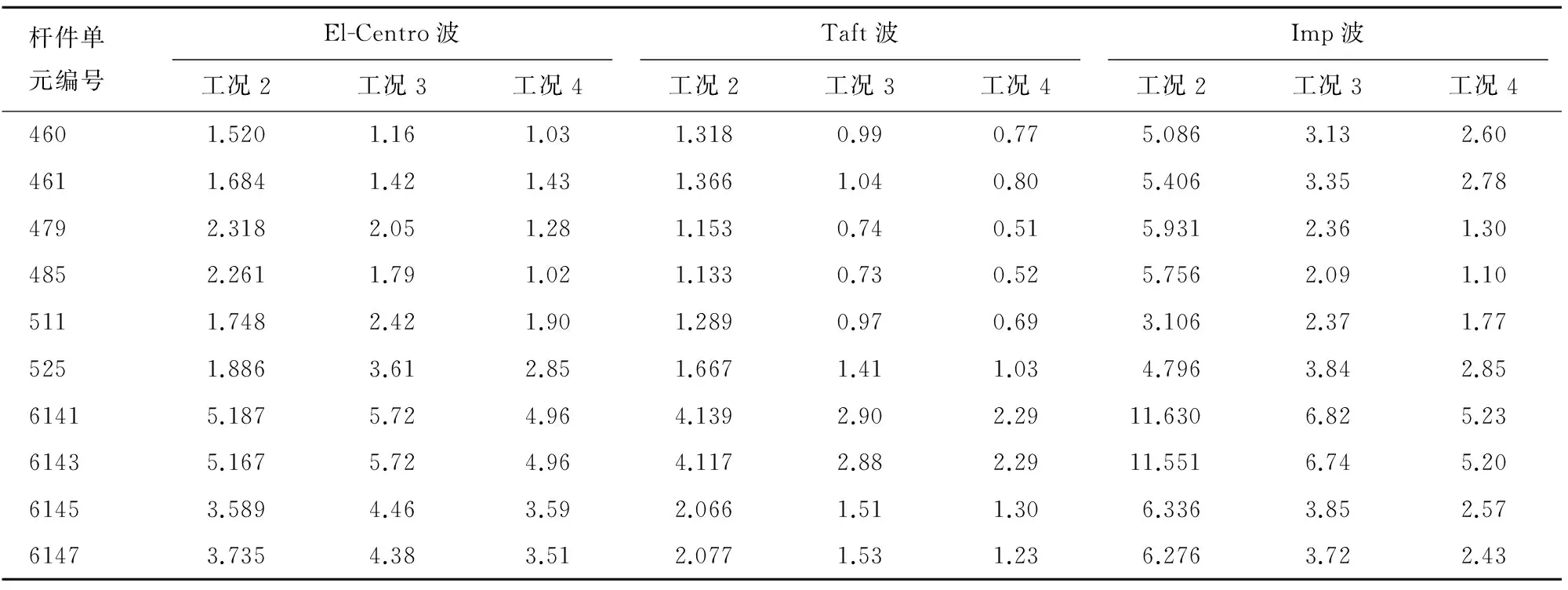
表10 部分杆件应力的影响系数Tab.10 Effect coefficient of stress of members

4 结论

研究了某大跨桥梁在一致激励和行波激励下的位移和内力变化，并对两种情况做了对比，结果表明：

1) 一致激励时结构的总体位移较小且不同位置处变化不大，左边跨相对于中间跨和右边跨而言位移较大；而考虑行波效应时，结构由左至右相对位移逐渐增大，变化明显，右边跨位移最大，行波效应影响系数由左至右逐渐增大，均大于1，说明考虑行波效应会使结构相对位移增大。

2) 一致激励时2号桥墩基底剪力值最大，1号桥墩基底剪力最小；考虑行波效应时，1号、2号、3号桥墩基底剪力值相差不大，4号桥墩基底剪力值最大。考虑行波效应时，各桥墩基底剪力均显著增大，设计时应考虑行波效应的影响。

3) 一致激励时桥墩处斜向杆件应力明显小于上部杆件和桥墩处平行杆件应力，上部杆件中左边跨杆件比中间跨和右边跨杆件应力大，斜向杆件中右边跨左墩处的杆件应力比其他部位的应力大；考虑行波效应时，桥墩处斜向杆件应力明显小于上部杆件和桥墩处平行杆件应力，上部杆件中左边跨和中间跨杆件比右边跨杆件应力大；平行杆件中左边跨左墩处杆件应力比其他4个部位杆件应力大，斜向杆件中右边跨左墩处的杆件应力比其他部位杆件应力大，平行杆件的应力明显大于斜向杆件的应力，但平行杆件的应力增大幅度比斜向杆件小。考虑行波效应时，与桥墩连接的局部杆件内力增大明显，支座处杆件设计时应考虑行波效应的影响。

4) 考虑波速分别为300、600和900 m/s时，随着波速增加，同一节点的相对位移减小，各桥墩基底剪力逐渐减小，但行波工况下剪力均大于一致激励工况；随着波速增大杆件应力减小，但桥墩处杆件应力均比一致激励时为大。建议大跨度桥梁设计时应考虑行波效应的影响，尤其应注意低波速的影响。

参考文献：

[1]林伟,陈尚鸿,祁皑,等.多维多点激励下大跨度连体高层结构地震响应分析[J].福州大学学报(自然科学版),2011,39(6):923-929.

LIN Wei,CHEN Shanghong,QI Ai,et al.Seismic response of long-span connected structures under multi-support and multi-dimensional earthquake excitations[J].Journal of Fuzhou University(Natural Science Edition),2011,39(6):923-929.

[2]何庆祥,沈祖炎.结构地震行波效应分析综述[J].地震工程与工程振动,2009,29(1):50-57.

HE Qingxiang,SHEN Zuyan.Review of structural seismic analysis of traveling wave effect[J].Journal of Earthquake Engineering and Engineering Vibration,2009,29(1):50-57.

[3]田仲业,楼梦麟.多点激励反应谱法研究现状与发展[J].同济大学学报(自然科学版),2013,41(8):1119-1125.

TIAN Zhongye,LOU Menglin.State of research in response spectrum for multi-supported structures[J].Journal of Tongji University(Natural Science),2013,41(8):1119-1125.

[4]白凤龙,李宏男.地震动多点激励下大跨空间网架结构的反应分析[J].工程力学,2010,27(7):67-73.

BAI Fenglong,LI Hongnan.Seismic response analysis of long-span spatial truss structure under multi-support excitations[J].Engineering Mechanics,2010,27(7):67-73.

[5]石永久,赵博,陈志华,等.成都东客站钢结构多点地震输入响应分析[J].沈阳建筑大学学报(自然科学版),2014,30(1):1-8.

SHI Yongjiu,ZHAO Bo,CHEN Zhihua,et al.Time-history analysis of seismic response of Chengdu east railway station subjected to non-uniform ground motions[J].Journal of Shenyang Jianzhu University(Natural Science),2014,30(1):1-8.

[6]YAN X,GEORGE C.Traveling wave effect on the seismic response of a steel arch bridge subjected to near fault ground motions[J].Earthquake Engineering and Engineering Vibration,2007,6(3):245-257.

[7]闫晓宇,李忠献,韩强,等.多点激励下大跨度连续刚构桥地震响应振动台阵试验研究[J].土木工程学报,2013,46(7):81-89.

YAN Xiaoyu,LI Zhongxian,HAN Qiang,et al.Shaking tables test study on seismic response of a long-span rigid-framed bridge under multi-support excitations[J].China Civil Engineering Journal,2013,46(7):81-89.

[8]魏凯,郭平,韩萍,等.行波效应下多联长跨组合结构桥梁地震响应分析[J].结构工程师,2010,26(2):119-125.

WEI Kai,GUO Ping,HAN Ping,et al.Seismic response of a long multi-span composite bridge under traveling wave excitation[J].Structural Engineers,2010,26(2):119-125.

[9]闫斌,戴公连,徐庆元.行波效应下铁路简支梁桥梁轨系统地震响应[J].振动工程学报,2013,26(3):357-361.

YAN Bin,DAI Gonglian,XU Qingyuan.Seismic response of railway track-bridge system under traveling wave effect[J].Journal of Vibration Engineering,2013,26(3):357-361.

[10]王浩,李爱群.ANSYS大跨度桥梁高等有限元分析与工程实例[M].北京:中国建筑工业出版社,2014.