基于条件信息熵的超高维分类数据特征筛选

程国胜，孙超男，宋凤丽，来 鹏

（南京信息工程大学 数学与统计学院，南京 210044）

0 引言

随着现代技术的迅猛发展，大量的高维数据出现在各类领域中，比如生物影像、高频时间序列数据、肿瘤分类和经济预测等。在这些高维分类数据中，变量的个数p远大于样本量n，这种情形被称作“大p小n”。在高维数据分析中，经常引用稀疏性假设，即假设只有少量的协变量与响应变量相关，基于这样的假设，研究者们提出了一系列正则化的方法用于解决一般的高维回归分析，例如lasso[1]、SCAD[2]、elastic net[3]等方法。但这些方法均是处理当 p适中的情形，当处理超高维数据时，在计算花费、统计准确性和算法稳定性方面都面临很大的问题。受到这些挑战的启发，研究者们尝试把边缘特征筛选应用在超高维数据中，通过简便快速的方法进行超高维数据的初步降维，然后再利用一般的高维降维方法进行分析处理。Fan和Lv[4]提出用Pearson相关系数来进行特征筛选，并且证明了在线性模型假设下该方法具有确定筛选性质。Li等[5]提出根据距离相关系数将协变量排序，并证明出该方法（DC-SIS）在自由模型下同样具有确定筛选性质。Mai等[6]针对两类判别分析问题，提出基于Kolmogorov距离进行超高维变量特征筛选的方法，并且在模型假设很弱的情况下仍然具有确定筛选性质。Huang等[7]针对协变量与响应变量均为多类别变量的问题，提出一种基于自由模型用Pearson卡方检验进行特征筛选的方法，该方法具有确定筛选性质。

目前，大多数超高维变量筛选的文献都是基于协变量与响应变量之间的相关性构造相应的统计量来度量变量间是否独立，是否存在关联。Shannon[8]将信息熵和交互信息应用到信息论中，信息熵值越高意味着系统具有越高的不确定性或者可变性。2011年，Reshef等[9]在《Science》上发表了基于互信息进行相关性分析的文章，可有效地刻画了变量之间的非线性关系。于是，Ni等[10]提出一种基于互信息的超高维多类别变量的特征筛选方法，体现出互信息作为度量变量之间的非线性的有效性。

本文提出一种基于条件信息熵进行重要变量的筛选方法，从信息量的角度来构造相应的统计量进行相关性分析，证明了在自由模型下该方法具有确定筛选性质，且具有计算简单快速的优点。从模拟的结果来看，针对响应变量与协变量均为离散型类别数据，筛选结果相对于其他一些方法有更好的效果。

1 条件信息熵（CIES）

众所周知，在信息系统中，信息熵是描述信息内容的有效方法。德国物理学家Clausius在1850年首次提出用熵来测量空间中能量分布的均匀程度，能量分布越均匀，那么对应的熵值越大[11]。根据该原理，信息熵之父Shanon提出用信息熵来描述平均信息量[8]，同时也用数学语言对信息熵进行了描述，即离散型随机变量X的信息熵为，其中 pk为随机变量 X=xk的概率pk=P（X=xk）。本文提出用条件信息熵来衡量给定响应变量条件下，协变量所包含的信息量，进一步筛选出与响应变量相关性较强的协变量。

设响应变量Y 为二元变量，即Y=0，1,且 X=(X1，X2，…，Xp)T为 p维协变量，由于变量维数 p关于样本量n成指数型增长要从这p维协变量中筛选出与响应变量Y相关性比较强的变量。通常会有稀疏性假设，即假设只有少量协变量与响应变量相关。设重要变量子集和不重要变量子集分别为D和Dc为重要变量集合的大小，其中 D={j:对某些Y=y，Xj与 F(Y|y)相关}，

本文利用信息熵从信息量的角度出发来讨论协变量Xj与响应变量Y之间的相关性。协变量Xj的信息熵为其中pj，l=P(Xj=l),j=1，…，p;l=1，…，L为协变量Xj的概率分布。相应地，给定Y条件下Xj的条件信息熵H(Xj|Y)为：

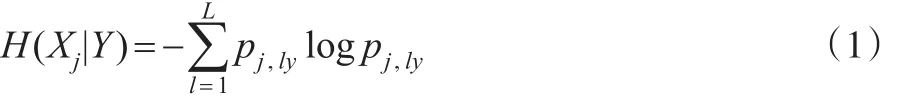
其中 pj，ly=P(Xj=l|Y=y)表示给定Y=y条件下 Xj=l的条件概率分布。

据此，定义如下的筛选指标来衡量Xj与Y之间的独立性：

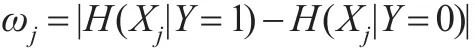
从信息熵角度考虑，如果协变量Xj与响应变量Y独立，则有给定Y=0条件下Xj的条件信息熵与给定Y=1条件下Xj的条件信息熵相等，即ωj=0；如果不独立，则有ωj＞0。因此可以根据ωj的大小来筛选与响应变量相关性较强的协变量。为了计算ωj，需要给出其样本估计量。假设给定n组观测值，有：

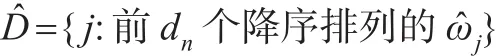
其中dn为预设的模型大小，满足dn≤n。在一些特征筛选文章中，阈值dn一般设为[n/logn]，其中[a]表示a的整数部分。

为了验证简化模型D是否包含所有真实的重要协变量，下面研究条件信息熵筛选（CIES）的确定筛选性质。首先，建立确定筛选性质需满足以下三个正则化条件：

（C1）协变量 X的维数 p和样本量n满足logp=na，其中

（C2）存在两个正常数0＜c1＜c2＜1使得

注：Cui,H.等[12]在所写的超高维自由模型判别分析文章中也做出了（C2）同样的假设，该条件确保响应变量Y和协变量X每个类别的比例不会太小也不会太大。（C3）这类型的假设条件在特征筛选文献中非常典型，例如文献[12]中的（C2）都是这类的假设。

定理 1（确定筛选性）:在（C1）、（C2）条件下。对0≤τ＜1/2，存在正常数c有：

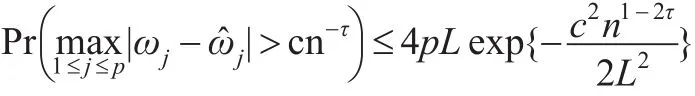
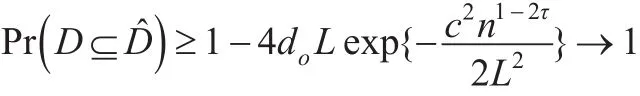
其中p为协变量X的维数，n为样本量，L为变量Xj的类别数。

2 数值模拟

协变量X为离散型变量，响应变量Y为服从均匀分布的两类别离散型变量，真实模型D={1 ，2，3} ，设定预测模型大小。在给定 yi=r的条件下，定义相关的类别变量概率为r=1，2，1≤k≤d0，表1给出了 θrk的取值。对于任意的r=1，2，d0＜k≤p，设 θrk=0.5。分别考虑 n=100;150;200，p=1000;2000几种情形。

表1 模拟的参数设定

本文通过以下准则将CIES的模拟效果与PC-SIS、IG-SIS进行比较：MMS，即包含所有重要变量的最小模型大小；P，当估计模型大小为12时，其包含所有重要变量的概率。

表2（见下页）给出了三种方法模拟500次，5%，25%，50%，75%，95%分位点的MMS值，以及所选模型包含所有真实重要变量的覆盖比。从模拟结果来看，CIES方法的模拟效果比较好，随着样本量n的增加，MMS值更加接近真实模型大小，并且覆盖比P趋近于1。对于两类别的离散型协变量，CIES方法的效果相对于PC-SIS、IG-SIS方法好一些，尤其是当样本量较少时，CIES方法更加适合用来进行超高维特征筛选。

3 定理证明

为了证明定理1，首先介绍下面的引理。

引理1（Hoeffding’s不等式）：设 X1，X2，…，Xn为独立随机变量。假设，其中ai，bi为常数。设，则对于正常数t有下面的等式成立：

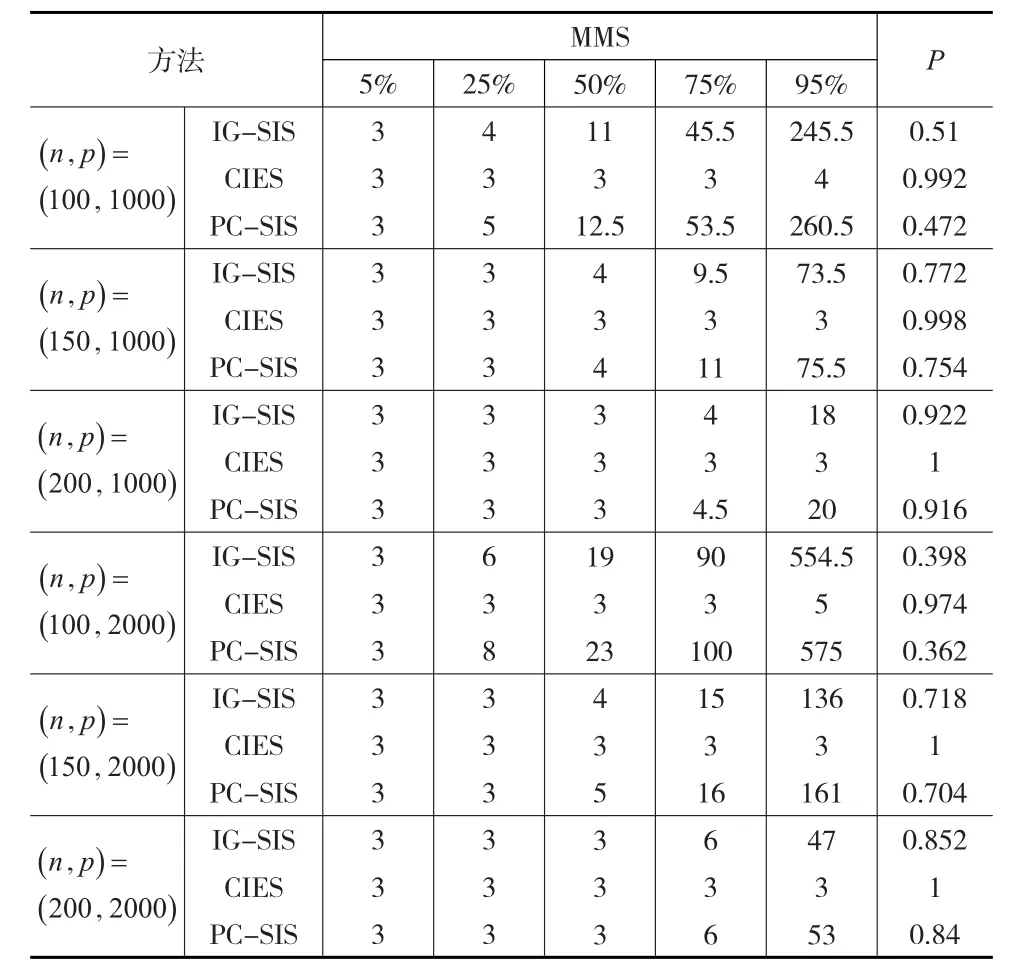
表2 模拟结果

引理2：假设a和b为两个有界随机变量，也就是说，存在常数M1＞0,M2＞0使得。给定样本大小分别为a和b的估计值。假设对于，存在正常数 c1，c2和 s，使得：

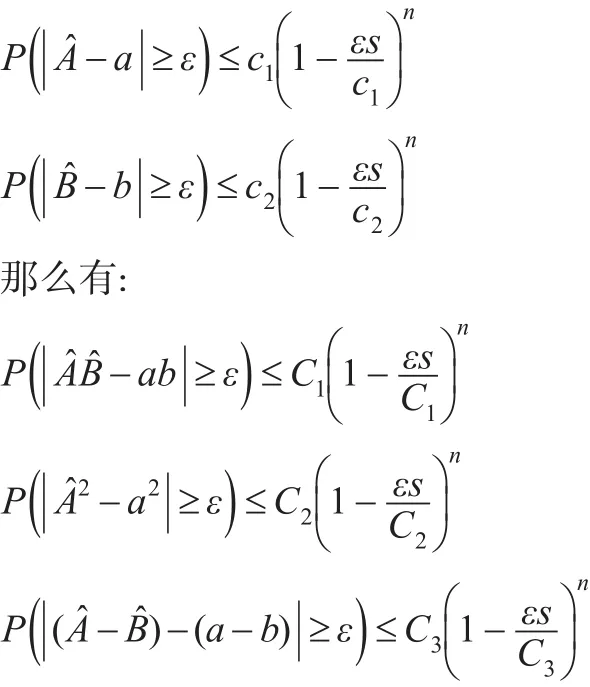
此外，假设 b有界且不为0，即存在 M3＞0使得，那么有：

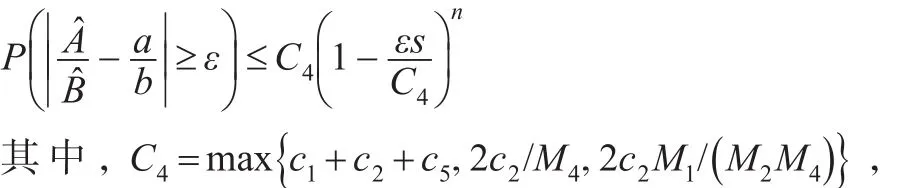
c5和M4均为正常数，且在证明中有所定义。

对定理1的证明：根据ωj和的定义，有：

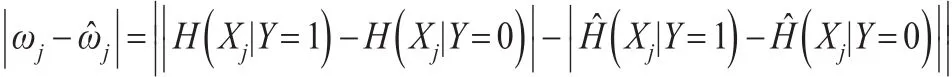
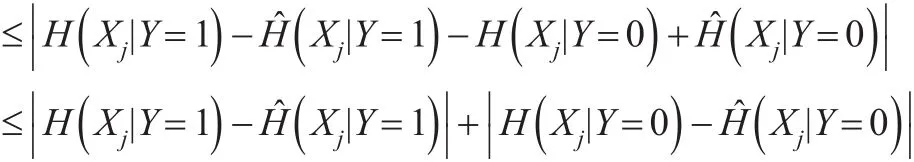
那么有：

下面来证明如下不等式：

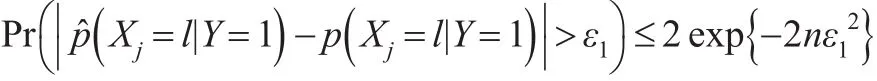
利用每类样本的频率来估计概率，这样有：

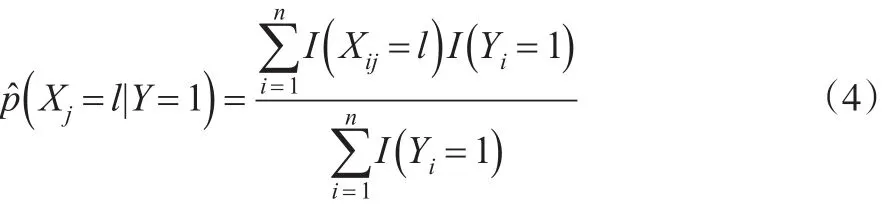
此外，有：

结合式（4）和式（5），进一步有：

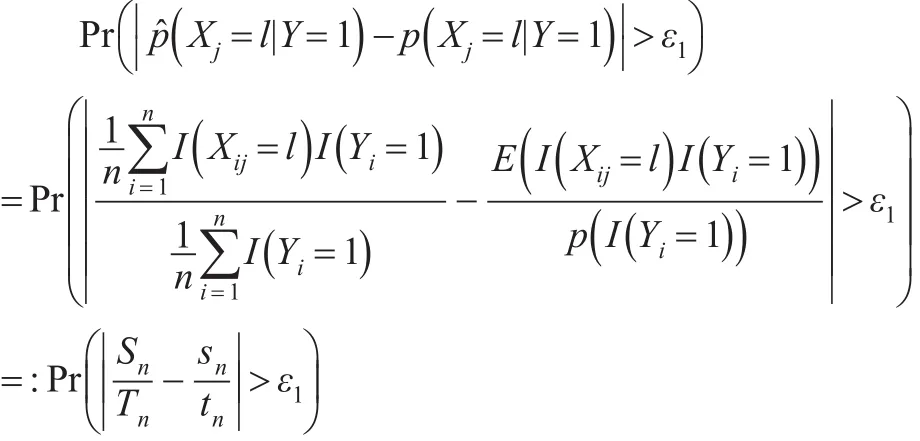
根据引理2，证明将进一步转化为证明Sn，Tn为sn，tn的估计值。由引理1，可得：

因此对于概率函数 p*及其估计值 p*，有 p*依概率收敛到 p*。同样可以证明logp*依概率收敛到logp*：

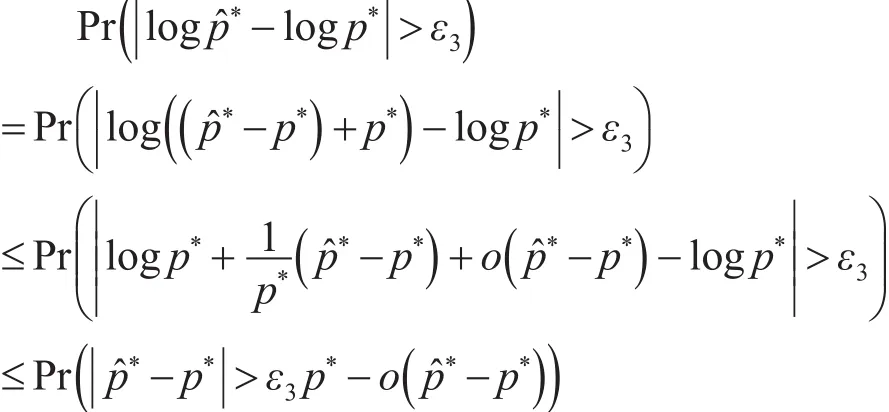
同样地，可以简单地证明Ej2部分，有：

因此：

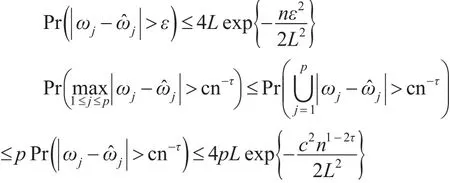
对0≤τ＜1/2，存在正常数 c，当0＜a＜1-2τ时随着n→+∞有

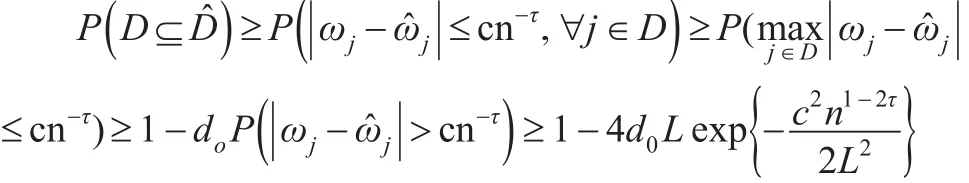
4 结论

本文提出了一种基于条件信息熵进行超高维自由模型特征筛选的方法，证明其具有确定筛选性质。从模拟的结果来看，当协变量X和响应变量Y均为两类别时，此方法相对于其他筛选方法有更好的筛选效果。在后续的工作中，将考虑协变量X和响应变量Y均为多类别离散型随机变量或者连续型随机变量的情形，尝试用区间分割将变量离散化，基于条件信息熵进行超高维特征筛选。

参考文献：

[1]Tibshirani R.Regression Shrinkage and Selection via the Lasso[J].Joumal of the Royal Statistical Society,1996,58(1).

[2]Fan J Q,Li R Z.Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties[J].Journal of the American Statistical Association,2001,(96).

[3]Zou H.Hastie T.Regularization and Variable Selection Via the Elastic Net[J].Journal of the Royal Statistical Society,2005,67(2).

[4]Fan J Q,Lü J C.Sure Independence Screening for Ultrahigh Dimensional Feature Space[J].Journal of the Royal Statistical Society,2008,70(5).

[5]Li R,Zhong W,Zhu L.Feature Screening via Distance Correlation Learning[J]Journal of the American Statistical Association,2012,107(499).

[6]Mai Q,Zou H.The Kolmogorov Filter for Variable Screening in High-dimensional Binary Classification[J].Biometrika,2013,(1).

[7]Huang D,Li R,Wang H.Feature Screening for Ultrahigh Dimensional Categorical Data With Applications[J].Journal of Business&Economic Statistics,2014,32(2).

[8]Shannon C E.A Mathematical Theory of Communication[M].New York:McGraw-Hill,1974.

[9]Reshef D N,Reshef Y A,Finucane H K,et al.Detecting Novel Associations in Large Data Sets[J].Science,2011,(344).

[10]Ni L,Fang F.Entropy-based Model-free Feature Screening for Ultrahigh-dimensional Multiclass Classification[J].Journal of Nonparametric Statistics,2016.

[11]Clausius R.Ueberverschiedene Fur Die an Wendungbequenme formen der Hauptgleichungen der Mechanischenwarmetheorie[J].Annalen Der Physik,2006,201(7).

[12]Cui H,Li R,Zhong W.Model-Free Feature Screening for Ultrahigh Dimensional Discriminant Analysis[J].Journal of the American Statistical Association,2015,110(510).