基于进化博弈的P2P平台与投资人的行为及仿真分析

张文远，邢 航

（北京工业大学 经济与管理学院，北京100124）

0 引言

影响P2P平台有效运作的缺陷，即必须保证经过P2P平台的借款能够按时还本付息，否则无法按时支付投资人本息。而一旦P2P平台对投资人违约，将无法获得资金用于借款人的借款。有效运作的P2P平台必须具有两个方面的能力：（1）强有力的风控体系；（2）良好的资金来源渠道。与商业银行类似，P2P平台以中介身份，对借款进行撮合交易，因此，P2P平台既需要风险可控的优质资产，也需要良好的资金来源渠道。因此，投资人的客户质量，客户来源多样化同样影响着P2P平台发展。

本文尝试运用进化博弈的理论分析P2P平台与投资人的行为，为P2P平台的合规运作提供建议。

1 进化博弈理论及模型假设

生态学家Smith J.M和Price G.R（1973）在生物进化的背景下结合经典博弈理论，提出了进化稳定策略（Evolutionarily stable strategy,ESS）。

为了更好的分析P2P平台与投资人之间的利益关系并建立进化博弈模型，对该模型进行如下假定：

（1）P2P平台与投资人处于完全竞争市场，博弈双方存在足够多的选择。

（2）P2P平台管理者与投资人均为有限理性主体，个体的决策不断调整。

（3）投资人选择“投资”和“拒绝投资”的比例分别为X和1-X。X和1-X不是固定不变的，而是随着时间不断变化的函数X(t)和1-X(t)，为简化起见，写为X和1-X。同理，P2P平台选择“按时支付投资本息”和“不按时支付投资本息”两种决策的比例分别为Y和1-Y，其中0＜X＜1，0＜Y＜1。

根据上述假设，可以得到投资人，P2P平台博弈双方的支付收益矩阵如表1所示。

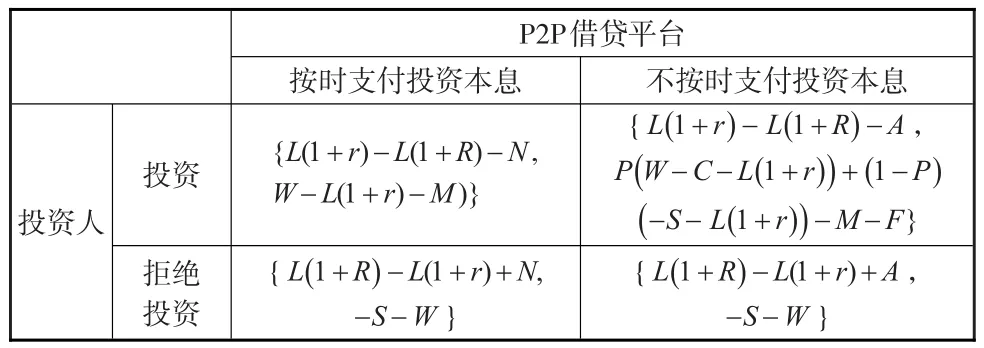
表1 投资人与P2P平台的支付收益矩阵

2 模型博弈过程与均衡分析

为了更好的分析投资人及P2P平台的行为模式，本文分别计算双方的收益。

2.1 投资人行为分析

由上述假设可推出，投资人选择“投资”和“拒绝投资”的概率分别为X和1-X。所以，可以根据表1得到以下期望收益函数：

投资人在选择“投资”的期望收益为：

投资人在选择“拒绝投资”时的期望收益为：

则投资人的平均收益为：

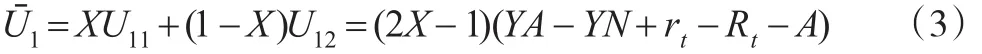
在投资人中对P2P平台“投资”的比例数为X的复制动态方程为：

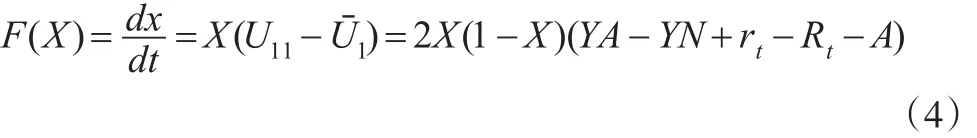
其中，dx/dt表示投资人选择“投资”策略比例随时间变化的比率。该比率表明，当投资人选择“投资”比例为X时的收益优于平均水平下的期望收益，则投资人中选择“投资”的比例会上升。

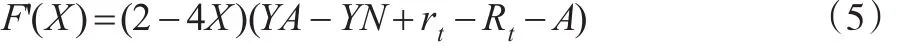
综合上述分析：当P2P平台选择“按时支付投资本息”时的比例时，投资人无论选择是否投资，两种决策的收益都是相同的。当Y＞(Rt-rt+A)/(A-N)时，投资人选择“投资”的收益会高于平均收益，投资人最终会全部选择投资。当时，投资人选择“拒绝投资”的收益会高于平均收益，投资人最终会全部选择“拒绝投资”。

2.2 P2P平台行为分析

根据上文假设，P2P平台选择“按时支付投资本息”和“不按时支付投资本息”两种决策的概率分别为Y和1-Y，则根据表1支付收益矩阵可以得出：

P2P平台在选择“按时支付投资本息”时的期望收益为：

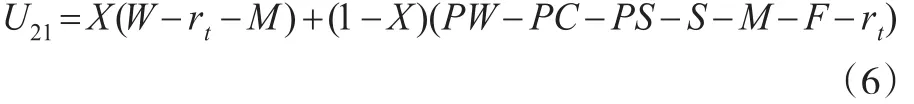
P2P平台在选择“不按时支付投资本息”时的期望收益为：

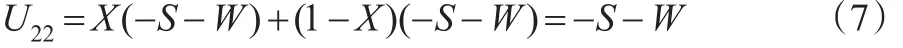
P2P平台的平均收益为：

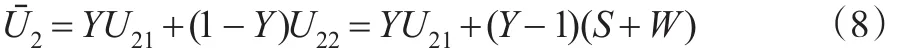
P2P平台在选择“按时支付投资本息”时比例为Y时的复制动态方程为：

其中，dy/dt表示P2P平台采取“按时支付投资本息”策略比例和时间变化的比率。当P2P平台选择“按时支付投资本息”比例为Y时的收益优于平均水平下的期望收益，则P2P平台中选择“按时支付投资本息”的比例会上升。

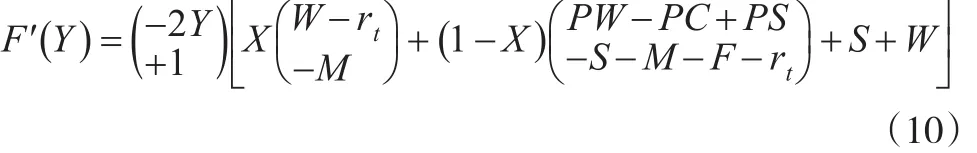
综合博弈双方的复制动态方程，可得到图1（见下页）：

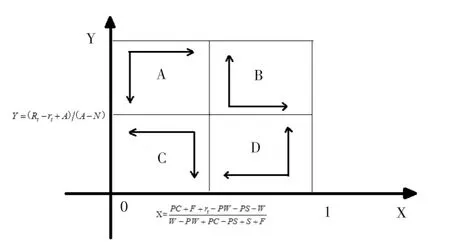
图1 基于两方程的动态博弈演化轨迹

X=0，Y=0和X=1,Y=1，为投资人和P2P平台长期动态博弈的进化稳定策略。在博弈过程中，当博弈双方选择比例的动态点E落在C区域中时，进化稳定策略为X=0，Y=0。即投资人选择“拒绝投资”策略，P2P平台选择“不按时支付投资本息”策略。当动态点E落在图中B区域，X=1,Y=1为此时进化稳定策略，即投资人选择“投资”策略，P2P平台选择“按时支付投资本息”策略。而当投资人与P2P平台的动态点E落在A,D区域中，双方经过长期动态博弈后，最终会收敛的进化稳定状态并不确定。这将根据和y0=(Rt-rt+A)/(A-N)的数值来确定。根据图5可知系统的5个稳定点分别是：E1（0,0），E2（0,1），E3（1,0），E4（1,1）E5（x0,y0）。但是这5个状态并非都是系统的进化稳定策略ESS。接下来需要对策略均衡点进行局部稳定性分析。当稳定点满足条件行列式的值大于零（det.J＞0），迹小于零（tr.J＜ 0）才可确定该策略是进化稳定策略。

根据定义雅克比矩阵为：

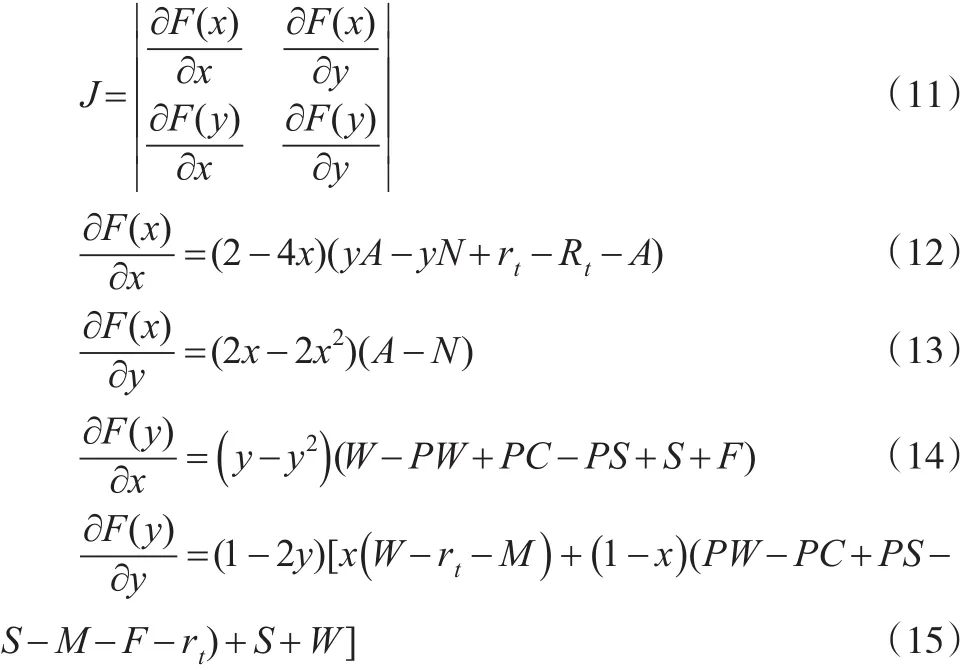
则可得出该系统下的P2P网络借贷平台与投资人的均衡点及稳定性，见表2。

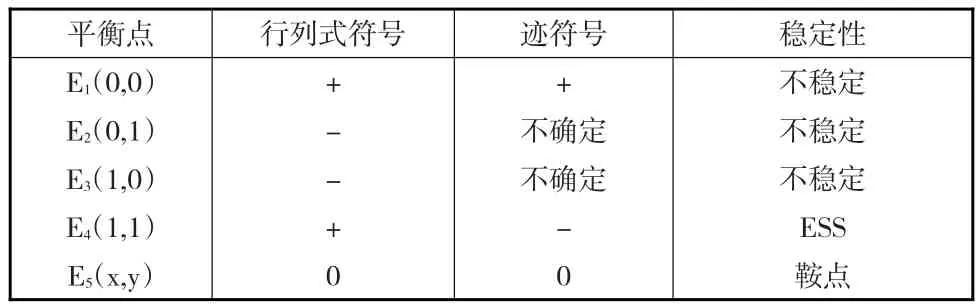
表2 博弈均衡点及稳定性分析

根据雅克比矩阵对5个平衡点进行局部稳定性分析后，如表2所示，系统在E4（1,1）才具有局部稳定性。即当投资人倾向于同意投资，P2P平台倾向于按时支付投资本息时，才是双方的的最佳策略，双方的所得收益均大于平均收益。

2.3 博弈双方的行为仿真模拟分析

为了更好地了解模型中的主要参数对投资者及P2P平台的行为变化的影响，本文运用MATLAB对影响博弈双方行为的各项参数进行分析。

（1）贷款数额L。在其他参数不变的情况下，随着L的不断增加，选择X和Y的比例均随之下降，X的斜率变化更大。由此可说明，随着贷款金额的不断增大，投资人选择“投资”的比例逐渐下降，同时P2P平台中选择“按时支付投资本息”的比例也随之下降，且投资人受到的影响比平台受到的影响更大。图2揭示了P2P小额借贷的发展趋势。

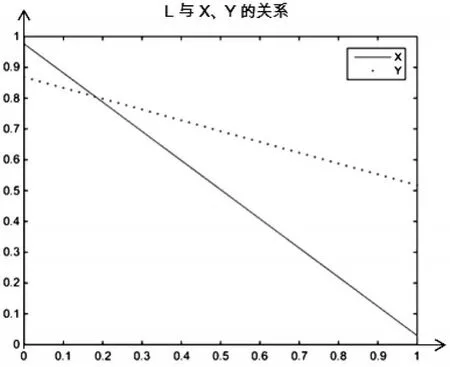
图2 随L变化的博弈双方决策变化图

（2）P2P平台需支付的利率rt。同理，随着rt的增加，该图形表现为X逐渐上升，Y逐渐下降（见图3）。说明了随着本息的逐渐增加，投资人选择投资的比例越来越高，而P2P平台由于利率的上升，存在不按时支付投资本息的比例逐渐增大。

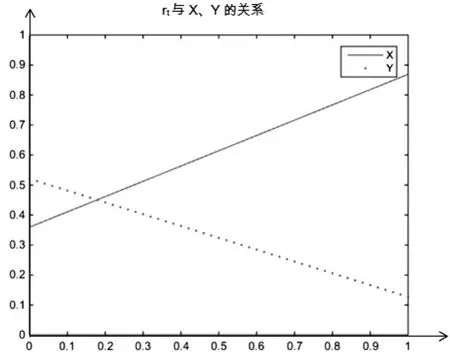
图3 随rt变化的博弈双方决策变化图

（3）银行等正规金融机构的存款利率Rt。同理，随着Rt的增加，X不变，而Y逐渐下降（见下页图4）。说明银行存款利率的上升对投资人的决策无影响，而P2P平台选择“按时支付投资本息”的比例随之下降。这是由于银行活期存款利率固定，不会影响投资者的决策。而P2P平台不按时支付投资本息的比例增加，原因在于平台违规挪用投资人的资金带来的收益要高于所付出的的成本。

（4）P2P平台初始的注册资本金S。同理，随着S的上升，Y的值不变，X的值随之下降（见下页图5）。也就是说，平台的注册资金越高，选择投资的比例会逐渐下降，而对按时支付投资本息的选择无影响。由于平台自身注册资金越高，平台在设立时可以申请的业务范围就会扩大，可以拥有平台自身的借贷业务，如人人贷此类的线上线下相结合的业务模式。这时，平台自身就会充当投资者的角色对借款人进行放贷，从而降低了投资者选择“投资”的比例。

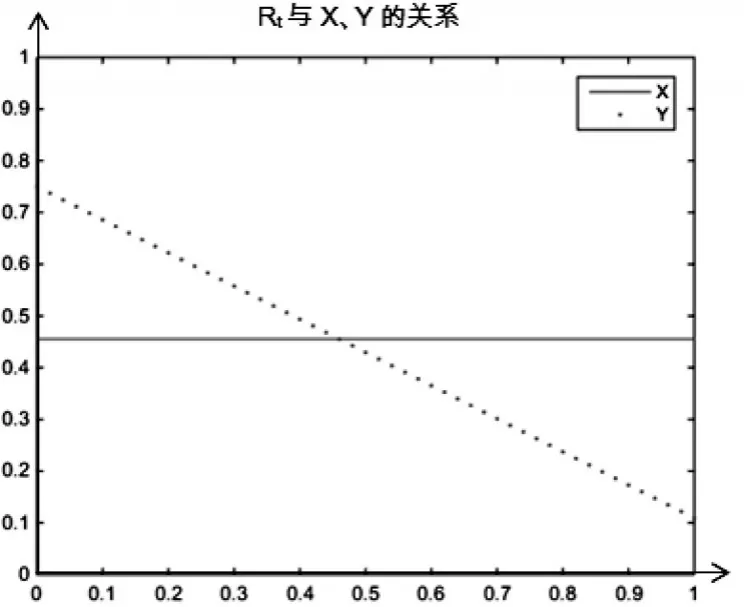
图4 随Rt变化的博弈双方决策变化图

图5 随S变化的博弈双方决策变化图

（5）P2P平台运营收益W。同理，随着W的增加，X逐渐增加，且斜率越来越小，Y不变（见图6）。说明了随着P2P平台运营收益的增加，可以增强投资者的投资信心，且选择“投资”策略的速度逐渐放缓。另外，平台收益对平台选择无影响，也就是说只要平台存在运营收益，就不会改变平台策略的因素。

3 结论及建议

根据MATLAB模拟仿真结果可以看出：（1）P2P平台的注册资金和营业收益会增强投资者的信心；（2）当贷款数额较大时，投资者倾向于不投资；（3）在其他条件不变的情况下，投资者会倾向投资于风险高，利率高的贷款；（4）当平台自身违约所受到的约束或惩罚较低时，就会倾向选择违约。

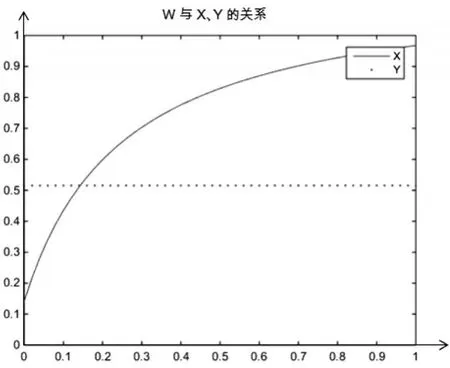
图6 随W变化的博弈双方决策变化图

基于上述分析，本文建议采取以下举措，降低P2P平台的坏账率，提升按时支付投资人本息的能力。

（1）P2P平台的客户群定位应为资金需求小的客户，依据大数法则通过增大用户数量分散风险。

（1）建立有效的风控体系，包括风险保证金制度、增加抵押贷款比例、健全客户准入及评审体系、建立有效的催收体系等。现阶段发展较好的P2P平台，如人人贷、微贷网等，均管理规范。

（3）强化监管部门对P2P的监管。增加P2P行业进入门槛，加强注册、牌照申请、高管任职要求、风控体系、日常经营等多维度的监管，通过定期和不定期的自查、抽查、专项检查等举措，提高P2P平台的违约成本，且一旦违规，对平台进行严厉处罚，以减少损害投资人现象的发生。

参考文献：

[1]Smith J M,Price G R.The Logic of Animal Conflicts[J].Nature,1973,11(246).

[2]韩斯玥,黄旭,贺本岚.国际P2P行业发展趋势与商业银行未来发展[J].金融论坛,2014,(3).

[3]禹海慧.我国P2P网络贷款平台的弊端及管理[J].中国流通经济,2014,(2).

[4]王会娟,廖理.中国P2P网络借贷平台信用认证机制研究——来自“人人贷”的经验证据[J].中国工业经济,2014,(4).

[5]廖理,李梦然,王正位.聪明的投资者:非完全市场化利率与风险识别——来自P2P网络借贷的证据[J].经济研究,2014,(7).

[6]缪莲英,陈金龙.P2P网络借贷中社会资本对借款者违约风险的影响——以Prosper为例[J].金融论坛,2014,(3).

[7]帅青红.P2P网络借贷监管的博弈分析[J].四川大学学报:哲学社会科学版,2014,(4).

[8]俞林,康灿华,王龙.互联网金融监管博弈研究:以P2P网贷模式为例[J].南开经济研究,2015,(5).