矿用通风机叶片裂纹诊断方法的研究

王 燕 马文文

通风机作为矿山安全生产的主要技术装备，是矿井通风系统的重要组成部分，是矿井安全生产和灾害防治的基础。风机质量的优劣，运行安全稳定与否都至关重要。叶片是通风机的关键部件，其性能好坏直接影响整机运行的效率和稳定性。裂纹是叶片故障中最常见的一种，叶片裂纹故障严重影响叶轮机械的经济和安全运行，如何以简单的方法和较高的准确率在线实时预报叶片裂纹故障，是困扰国内外设备故障诊断工程界和学术界的难题。

现有的叶片裂纹故障诊断方法主要分为两类：基于专家系统的方法和基于振动特征量的方法。对于现场在线测量来说，相对于振型和振型差值曲率来说，固有频率的变化量作为故障特征被更多地应用于裂纹故障的诊断上。

学者们对使用固有频率变化量诊断裂纹故障进行了大量研究[1-3]。当系统的边界条件变得更加复杂时，连续性求解方法不容易计算出其精确解。

因此本文提出一种裂纹叶片离散数学模型，这种数学模型可以更加直观的看出裂纹深度和位置对固有频率的影响。本文的目的是提出一种有效的矿用通风机叶片裂纹故障诊断方法。由于大型矿用通风机叶片的裂纹故障样本数据不易获得，本文根据裂纹叶片离散数学模型，应用传递矩阵法计算出叶片在不同裂纹情况下的前三阶固有频率。将其作为故障特征，反向求解出裂纹的位置和深度。本文提出的数学模型的准确性和诊断方法的有效性将通过实验验证。

1 故障诊断原理

当叶片上出现裂纹时，叶片的固有频率的变化只与裂纹深度和位置有关系。本文提出的故障诊断方法选择叶片的固有频率作为故障特征，通过对固有频率的反向求解，诊断出裂纹深度及其所在位置。

1.1 完好叶片模态分析

通过模态分析可以计算出叶片的固有频率。叶片通过叶根固定安装在叶轮上时，等直矩形截面叶片可视为固支悬臂梁。本文以某型通风机直叶片为研究对象，叶片裂纹为横向开口裂纹，本文不考虑阻尼的影响。叶片长L=500 mm，宽H=180 mm，厚度B=1.5 mm，密度r=7 930 kg/m3，弹性模量E=190 Gpa，可以视为矩形截面的欧拉-伯努利梁，叶片结构如图1所示：

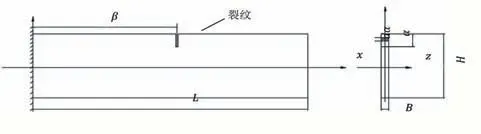
图1 裂纹叶片结构

根据机械振动学中的理论可知，悬臂梁前三阶固有频率分别为：

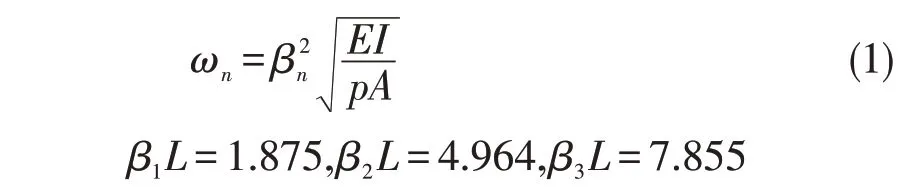
1.2 裂纹叶片模态分析

当叶片上存在裂纹时，通过引入“等效刚度”或“等效柔度”来体现裂纹的效应。由文献[14]的分析可知，叶片单裂纹处的等效柔度c为：

其中γ=α/H，α 为裂纹深度。

由(3)式可以看出，当叶片宽度不变时，单裂纹处的等效柔度c只与裂纹深度α 有关。

当叶片上存在裂纹时，叶片的边界条件变得更加复杂。此时若依旧将叶片结构视为连续系统，很难准确计算出裂纹叶片的固有频率。本文将提出一种裂纹叶片离散数学模型，利用传递矩阵法来计算其固有频率。当叶片上存在裂纹时，裂纹处左右的转角不相等，可通过考察裂纹左右转角值来计算裂纹叶片固有频率。

将整个叶片结构离散成若干个质量单元Z，每个单元包含一个无质量梁段和一个集中质量，如图2 所示。每个离散单元包含4个观察量，即Z=(yθMQ)，其中y、θ、M、Q分别为截面位移、转角、弯矩和剪力。

假设裂纹存在于第i个集中质量处，首先对第i个单元的无质量梁段做受力分析，如图3所示。

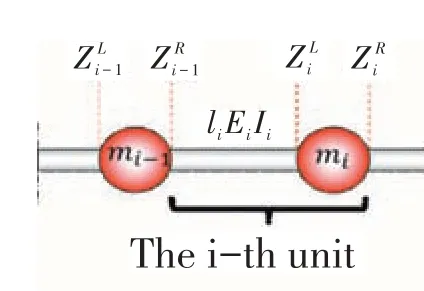
图2 第i个单元示意

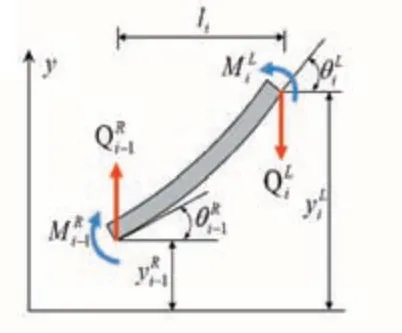
图3 第i个无质量梁段的受力分析

通过理论分析，可以发现当叶片上存在一简单裂纹时，叶片固有频率的值会受裂纹深度α 和裂纹位置β 影响。因此叶片的固有频率可视为以裂纹深度α 和裂纹位置β 为自变量的函数值。叶片的裂纹定量诊断是通过对固有频率值的反向求解实现的，即确定关系式：

2 故障诊断方法

本文提出的故障诊断方法主要分三步：生成故障样本、构造故障样本数据库、故障诊断。

首先，按照理论数学模型计算通风机叶片在不同裂纹情况下的前三阶固有频率，利用固有频率做故障特征。

其次，利用Matlab构建故障样本数据库，以裂纹位置β 为x 轴，裂纹深度α 为y 轴，叶片固有频率值为z轴，使用插值拟合曲线分别构建不同健康程度叶片的故障样本数据库，即叶片前三阶固有频率解曲面。

最后，将待诊断叶片测得的固有频率输入进故障样本数据库中进行故障诊断，反向求解确定裂纹的深度和位置。

3 实验验证

以某型矿用通风机等截面叶片为实验对象，实验系统由矩形等截面叶片、加速度传感器、力锤、数据采集与分析系统构成，如图4 所示。实验对象为9 种不同裂纹情况的叶片及一片完好叶片，其中裂纹位置β=125 mm、裂纹深度α=80 mm 的叶片为验证叶片，其余8种裂纹叶片为故障样本。叶片裂纹由激光切割技术完成，裂纹宽1 mm。

对称的在叶片上布置4个加速度传感器，如图5所示。力信号接入采集系统第一通道，4 个加速度信号依次接入第二、三、四、五通道，使用橡胶锤头力锤进行锤击法测固有频率实验。数据采集及处理系统为INV3020C，采集频率为12.8 kHz。

图4 实验系统布置

图5 传感器布置

根据理论计算方法与锤击实验获得的每种裂纹情况下的叶片前三阶固有频率如表1所示。从表1中可以看出，理论计算与锤击实验所获得的叶片前三阶固有频率误差较小。

将利用理论计算方法所得的不同裂纹情况下的叶片前三阶固有频率输入进Matlab中，以裂纹位置β 为x 轴，裂纹深度α 为y 轴，叶片固有频率值为z 轴，使用插值拟合曲线分别构建不同健康程度叶片的前三阶固有频率解曲面，如图8所示。

当裂纹β=125 mm 和α=80 mm 处时，以理论方法计算获得的裂纹叶片前三阶固有频率（见表1）作为反向的输入，采用等高线法求解裂纹的位置和深度。将前三阶固有频率分别代入到图6中绘制出不同模态下的频率等高线，然后将三条等高线绘制在同一坐标平面上，则交点位置对应坐标(x,y)数值即为裂纹的位置和深度，所绘制的频率等高线如图7所示。

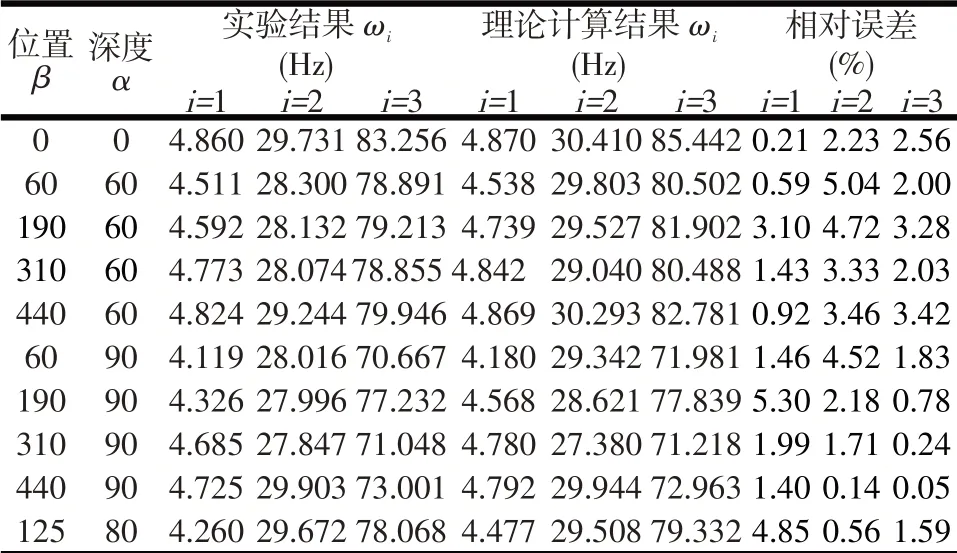
表1 叶片前三阶固有频率

图8为裂纹叶片固有频率随裂纹位置变化的关系曲线；图9 为裂纹叶片固有频率随裂纹深度变化的关系曲线，其叶片固有频率比值为裂纹叶片的固有频率ω0与完好叶片的固有频率ωc之比ω0。

图6 固有频率解曲面

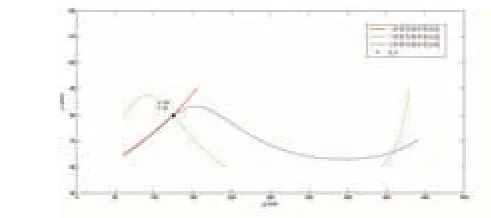
图7 频率等高线平面图

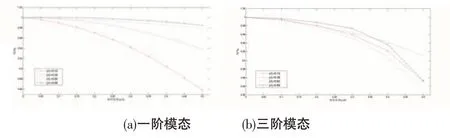
图8 裂纹相对深度(α/H)与结构固有频率比(ωC/ω0)关系曲线

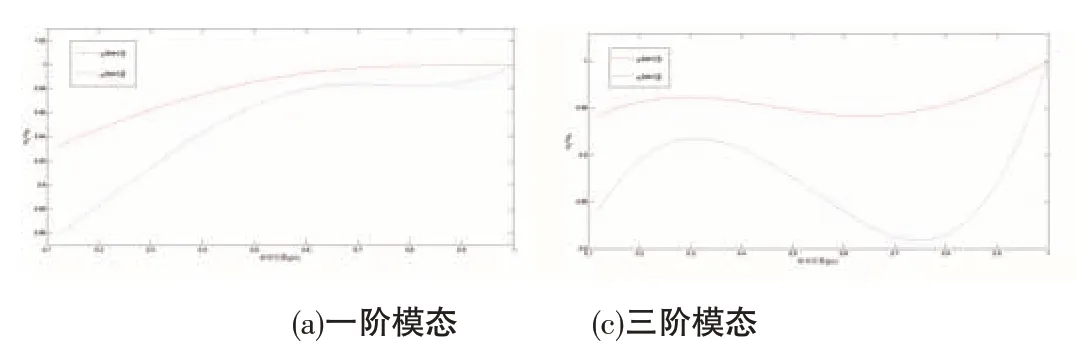
图9 裂纹相对位置( β/L)与结构固有频率(ωC/ω0)关系曲线

从图8、9中可以看出：

（1）裂纹的存在会减小结构的固有频率，测试中固有频率减低，可判断叶片上存在裂纹；

（2）对每阶模态，裂纹叶片的固有频率随裂纹深度的增加而减小，裂纹深度越深，叶片的固有频率越小；

（3）裂纹位置对固有频率的影响比较复杂，其中对于一阶模态，裂纹叶片固有频率随着裂纹相对叶根部距离的减小而减小；对于第二、三阶模态，固有频率的变化与这两阶振型的节点位置有关。

4 结论

本文提出一种裂纹叶片数学模型，通过计算其固有频率，并将计算结果与锤击实验结果进行对比，误差较小。在实用中测量风机的裂痕时，可进行锤击试验，测定固有频率，在通过反向求解可以准确定位到叶片裂纹的深度和位置。相比传统检验方法，本方法不受故障样本数所限，可以较准确的诊断出裂纹深度和位置。