补图是独立数为n-2的双圈图的最小特征值

芦兴庭，余桂东，严亚伟，孙 威

设G是一个n阶简单无向图，记其顶点集为V={v1,v2,…,vn} ，边集 E={e1,e2,···,em} 。 NG(v)表示G中与v相邻的点的集合，且记v的度数d(v)= | NG(v) |。设S⊆V，图G[S]表示以S为顶点集，以G中两端点均在S中的边为边集的图，称其为G的导出子图。若图G[S]中无边，则称S为G的独立集。G中含点数最多的独立集所含的点数称为G的独立数，记为 α(G)。记Gc=(V , Ec)为图G=(V ,E )的补图，其中

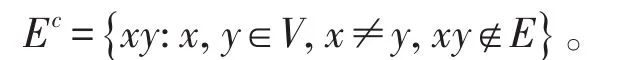
图G的度矩阵记为 D(G)=diag(d(v1),d(v2),···,d(vn) )，其中d(vi)是顶点vi的度数，i=1,2,…,n。图G的邻接矩阵为A(G)=(aij)n×n，如果vivj∈E，则aij=1；否则aij=0。图G的无符号拉普拉斯矩阵为Q(G)=D(G)+A(G )，因为 A(G)，Q(G)是实对称矩阵，因此它们的特征值是实数，故可排序。A(G)的最小特征值称为图G的最小特征值，不妨设A(G)的n个特征值从大到小排列为 λ1(G ) ≥λ2(G ) ≥…≥λn(G )，最大特征值 λ1(G)称为图G的谱半径，记作λmax(G )；最小特征值λn(G )称为图G的最小特征值，记作λ(G )，其对应的特征向量称作G的第一特征向量。由于Q(G)是半正定的，所以Q(G)的特征值从大到小排列为q1(G ) ≥q2(G )≥···≥qn(G )≥0，其中最大特征值q1(G)称为图G的无符号拉普拉斯谱半径；最小特征值qn(G)称为图G的无符号拉普拉斯最小特征值，记作a(G)，其对应的特征向量称作G的无符号拉普拉斯第一特征向量。

近年来，无符号拉普拉斯最小特征值的问题已经越来越受到重视，其中文献[1-4]研究了一类图的极小特征值，文献[5-10]研究了某一类特殊图的最小特征值；而文献[11-15]都是从补图的结构出发，分别研究了补图是树、单圈图、连通图、2-点（边）连通图的图的最小特征值，和补图是树、单圈图的无符号拉普拉斯最小特征值。受此启发，本文研究n阶且补图为独立数n-2的双圈图的最小特征值和最小无符号拉普拉斯特征值，并刻画了此类图最小特征值和无符号拉普拉斯最小特征值达极小的图。 G=(V ,E)为n阶简单图，对于向量X∈Rn，如果存在一个从V到X中值的映射φ，使得对于任意u∈V有Xu=φ(u)，则称X定义在G上。

对于任意向量X∈Rn，有

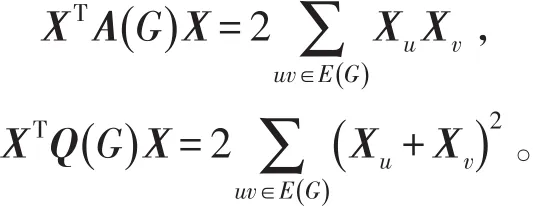
若λ是A(G)对应于特征向量X的特征值，则由特征值的定义，当且仅当X≠0时，对于每个v∈V ，有

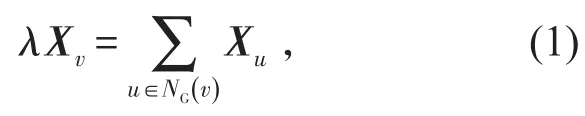
称（1）式为G关于X的特征等式。另外，对于任意单位向量X∈Rn，有

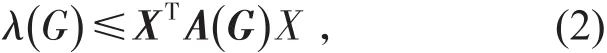
当且仅当X是G的第一特征向量时等号成立。

若q是Q(G)对应于特征向量X的特征值，则由特征值的定义，当且仅当X≠0时，对于每个v∈，有

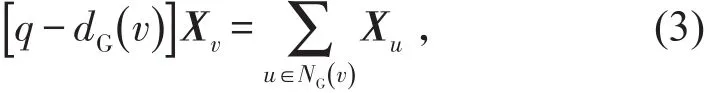
称(3)式为G关于X的无符号拉普拉斯特征等式。另外，对于任意单位向量X∈Rn，有

当且仅当X是G的无符号拉普拉斯第一特征向量时等号成立。

引理1[15]设G是一个简单图，有

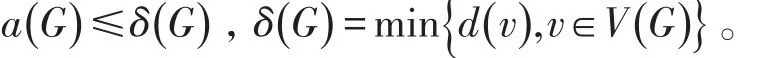
引理2[16]设A是一个实对称n×n阶邻接矩阵，邻接矩阵 B为 A的 m×m阶主子阵，且μ1(A )≥μ2(A )≥…≥μn(A),μ1(B )≥μ2(B )≥…≥μm(B)分别为A与B的特征值，则对于i=1,2,…,m，有μn-m+i(A )≤μi(B ) ≤μi(A)。

对于独立数为n-2的双圈图，它的双圈必共边，其两内圈为C3，外圈为C4，且两个内圈的公共点上分别悬挂 p个与q个悬挂点，其中p+q=n-4,p,q≥0，如图1所示，记为G(p ,q)。

图1 G(p ,q)

定理1 给定一个正整数n(n≥7)，对于任意的整数 p,q≥0且 p+q=n-4，则有

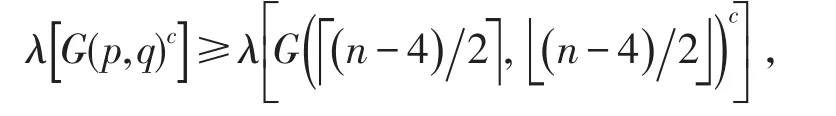
证明 设G(p ,q)如图1所示，X是G(p ,q)c的第一特征向量。由于K2是2点完全图，K2⊂G(p ,q)c，且λ(K2)=-1，根据引理2知≤-1。记X1:=Xv1，X2:=Xv2，X3:=Xv3，X6:=Xv6，根据(1)式知X2=X6；所有悬挂在v1上的点在X中对应的值相同，记作X4，所有悬挂在v3上的点在X中对应的值相同，记作X5，并且记λ:=

（i）若q=0，由（1）式可以得到

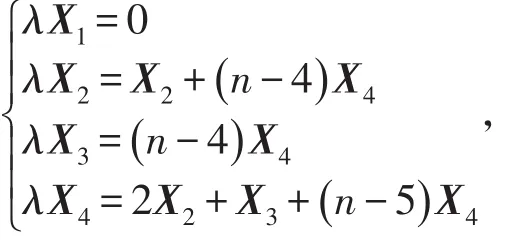
将上式转换成矩阵等式( )B-λI X'=0，其中

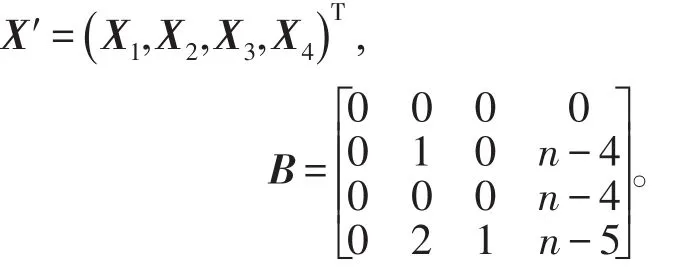
令f1(x ;n-4,0)=det(B -xI)，可以得到

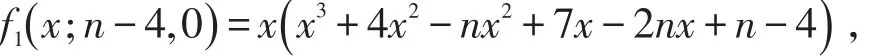
则λ为 f1(x ;n-4,0)=0的最小根。

当x=-1.8时，有

当n≥7时，有 f1(- 1.8;p,q) ＜0，从而λ＜-1.8。

（ii）若q≥1，由（1）式可以得到

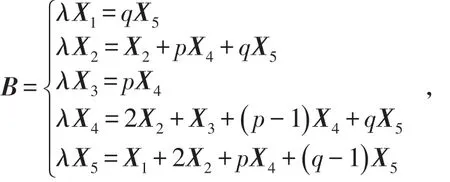
将上式转换成矩阵等式(B -λI) X′=0， ，其中

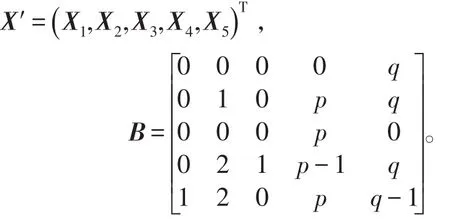
令f2(x;p,q)=det(B -xI)，可以得到

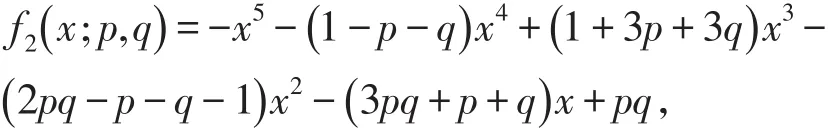
则λ是 f2( )

x;p,q=0的最小根。

当x=-1.8时，有

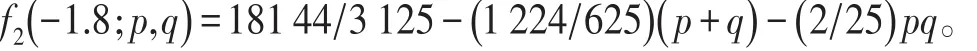
当n≥7时，p+q=n-4≥3，此时f2(- 1.8;p,q) ＜0，从而λ＜-1.8。当 p≥q+2，x＜-1.8时，有

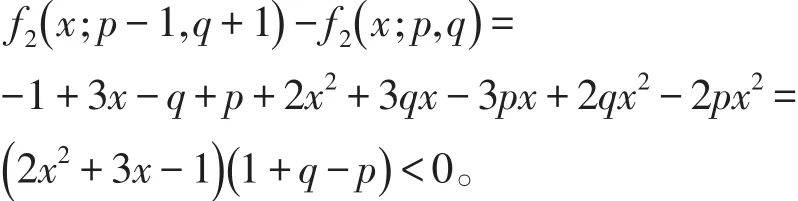
由于λ是方程 f2(x ;p,q)=0的最小根，从而有f2(λ ;p,q)=0，且 λ＜-1.8，由上式可得到f2(λ ;p-1,q+1) ＜0，这意味着

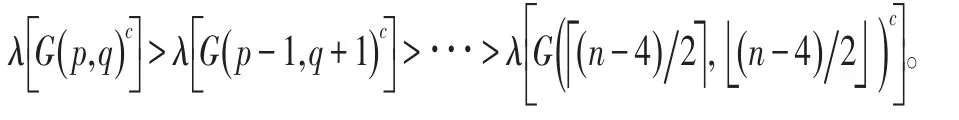
（iii）比较 λ[G ( n -4,0)c]与 λ[G ( n -5,1)c]的大小，设g(x)=f1(x ;n-4,0)(- x-1)=

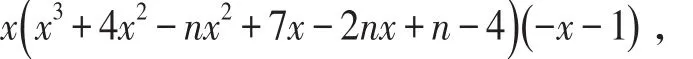
则有g(x)-f2(x ;n-5,1)=(n -5)(2 x2+3x-1)，这样，当 x＜-1.8，n≥7时，有g(x)-f2(x ;n-5,1) ＞0。由（i）（ii）知，λ[G ( n -4,0)c]＜-1.8，λ[G ( n -5,1)c]＜-1.8，即 λ[G ( n -4,0)c]＞λ[G ( n -5,1)c]，于是根据（i）（ii）（iii）知结论是成立的。

定理2给定一个正整数n(n≥7)，对于任意的整数 p≥q≥1且 p+q=n-4，有

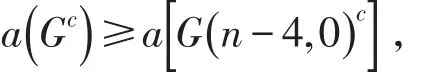
当且仅当G(p ,q)=G(n -4,0)时等号成立。

证明 G(p ,q)如图1所示，设X是G(p ,q)c的无符号拉普拉斯第一特征向量。由引理1知， 记 X1:=Xv， X2:=，

1X3:=Xv3，X6:=Xv6，根据(3)式知 X2=X6；所有悬挂在v1上的点在X中对应的值相同，记作X4，所有悬挂在v3上的点在X中对应的值相同，记作X5；并且记

由(3)式可以得到

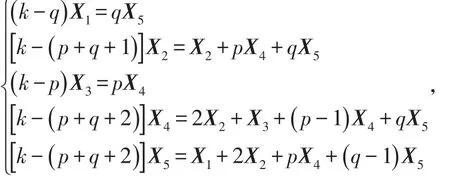
将上式转换成矩阵等式( )kI-B X'=0，其中

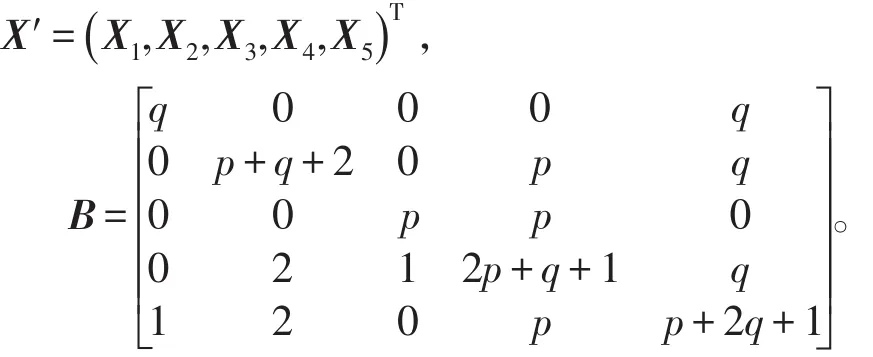
令f3(x ;p,q)=det(x I-B )，可以得到

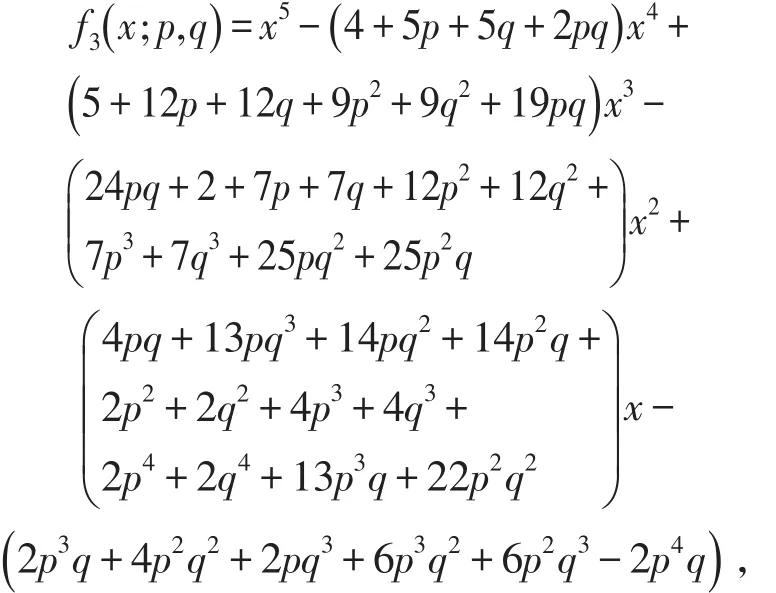
则k是 f3(x ;p,q)=0的最小根。

当 p≥q≥1时 ，有 f3(x ;p+1,q-1)-f3(x ;p,q)=(1 +p-q)(p +q-x)(x2-3qx-3px+2q2+4pq+2p+2q+2p2)。令

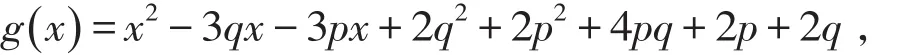
则有g'(x)=2x-3p-3q。

当0＜x≤q时，观察到 g'(x)是递增的，且有g'(x)≤g'(q)=-3p-q＜0，故此时 g(x)在0＜x≤q上单调递减，即有g(x)≥g(q)=pq+2q+2p+2p2＞0。

进一步有

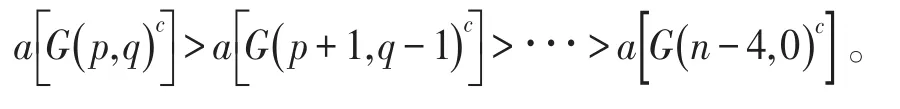
参考文献：

[1]BELL F K,CVETKOVIC D,ROWLINSON P,et al.Graph for which the least eigenvalues is minimal,I[J].Linear Algebra Appl,2008,429(8)：234-241.

[2]BELL F K,CVETKOVIC D,ROWLINSON P,et al.Graph for which the least eigenvalues is minimal,II[J].Linear Algebra Appl,2008,429(8)：2168-2176.

[3]CARDOSO D M,CVETKOVIC D,ROWLINSON P,et al.A sharp lower bound for the least eigenvalue of the signless Laplacian of a non-bipartite graph[J].Linear Algebra Appl,2008,429(11-12)：2770-2780.

[4]FAN Y Z,WANG Y,GAO Y B.Minimizing the least eigenvalues of unicyclic graphs with application to spectral spread[J].LinearAlgebraAppl,2008,429(2-3)：577-588.

[5]LIU R,ZHAI M,SHU J.The least eigenvalues of unicyclic graph with n vertices and k pendant vertices[J].Linear Algebra Appl,2009,431(5-7)：657-665.

[6]PETROVIC M,BOROVICANINB,ALEKSIC T.Bicyclic graphs for which the least eigenvalue is minimum[J].Linear AlgebraAppl,2009,430(4)：1328-1335.

[7]TANY Y,FAN Y Z.The vertex(edge)independence number,vertex(edge)cover number and the least eigenvalue of a graph[J].LinearAlgebraAppl,2010,433(2)：790-795.

[8]WANG Y,FAN Y Z.The least eigenvalue of a graph with cut vertices[J].LinearAlgebraAppl,2010,433(1)：19-27.

[9]YE M L,FAN Y Z,LIANG D.The least eigenvalue of graphs with given connectivity[J].Linear Algebra Appl,2009,430(4)：1375-1379.

[10]YU G D,FAN Y Z,WANG Y.Quadratic forms on graphs with application to minimizing the least eigenvalue of signless Laplacian over bicyclic graphs[J].Electronic Journal of Linear Algebra,2014,27(1081-3801)：213-236.

[11]FAN Y Z,ZHANG F F,WANG Y.The least eigenvalue of the complements of tree[J].Linear Algebra Appl,2011,435(7)：2150-2155.

[12]WANG Y,FAN Y Z,LI X X,et al.The least eigenvalue of graphs whose complements are unicyclic[J].Discussiones Mathematicae Graph Theory,2013,35(2)：1375-1379.

[13]YU G D,FAN Y Z.The least eigenvalue of graphs[J].Math Res Expo,2012,32(6)：659-665.

[14]YU G D,FAN Y Z.The least eigenvalue of graphs whose complements are 2-vertex or 2-edge connected[J].Operations Research Transactions,2013,17(2)：81-88.

[15]LI S C，WANG S J.The least eigenvalue of the signless Laplacian of the complements of trees[J].Linear Algebra Appl,2012,436(7)：2398-2405.

[16]HAEMERS W.Interlacing eigenvalues and graphs[J].Linear AlgebraAppl,1995,226-228：593-616.