巧“折”模型认识“角”——《角的初步认识》教学设计（二）

胡彩云

【教学内容】

苏教版二年级下册第84、85页。

【教学过程】

一、折纸游戏，创造角

师：同学们，今天我们一起来玩一玩折纸的游戏。（教师拿出一张特殊的纸，如下图）

师：看看这张纸的边缘，你有什么感觉？

生：不整齐。

师：把这张纸随便折一次，出现了什么？

生：出现了一条直直的边。

师：现在，再把这条折线对折一次，看看你会折出什么？

生：出现了一个角。

生：（自豪地）妈妈告诉过我，这是直角。

师：真了不起！像这样折一折，我们创造出一个直角的模型。（学生非常激动，仔细观察中）

师：用手指摸摸直角最顶端，你有什么感觉？

生：尖尖的、扎扎的、戳手。

师：这一点就叫做“顶点”。

师：从顶点出发，摸摸这两条折痕，你有什么发现？

生：很光滑、直直的。

师：这是直角的什么呢？

生：边。

师：这个直角有几条边？

生：两条。

师：谁来指一指，直角在哪里？

（学生借助直角模型，指角，有的学生指着顶点）

师：这个点就是直角吗？

师：（示范指角）大家看直角模型，直角就是从这个顶点出发，由这两条边组成的图形。

【设计意图：折纸是小学生喜欢的游戏，幼儿园的课程就有折纸。我们只要让学生折出一条直线，然后再对折，就能使学生迅速地利用身边最简单的材料创造出一个直角。先建立直角的概念，这样做的好处是学生生活中经常可见的是直角，表象丰富；之后我们通过与直角比较大小，能比较容易地扩展到其他角度。学生借助直角模型，摸一摸角的顶点、边，说一说摸到的感觉，多种感官认知方式的集合，直观地认识了角各部分的特点，自然地给角的各部分命名。】

二、借助模型，比较角

师：数学书封面上的这个角是直角吗？你是怎么判断的？

（学生展示比角的大小的方法，教师注意收集错误的比较方法，进行点评）

小结：将顶点重合，使一边重合，看看另一条边是否重合。

生：（异口同声）数学书封面上的角是直角！

师：数学书封面是什么形状？一共有几个直角？

生：数学书的封面是长方形，有四个直角。

师：拿直角模型和物体表面上的角比一比，哪些是直角？哪些比直角大？哪些比直角小？

（学生带着直角模型，离开位置活动，比较判断）

师：哪些物体的表面上有直角？

生：黑板面上有直角。

生：好像比直角大！

师：请你上来比给大家看！大家看看，黑板面上的这个角是不是直角？

（学生上来比一比，其他同学观察）

生：一样大！

生：窗户面上有直角。

生：地砖是正方形的，上面有四个直角。

师：有没有找到比直角小的角？

生：三角尺上的这个角比直角小。（三角尺上的锐角）

师：示范一下，你是怎么比的？

（学生操作）

师：（展示）顶点重合，一条边重合，另一条边在直角边的里面，说明这个角比直角小。

师：有没有找到比直角大的角？

生：（展示）这个五边形上的角比直角大，它的这条边在直角边的外面。

小结：想象一下，如果把角的两条边看作鳄鱼张开的嘴，大角的“嘴巴”张得——很大，小角的“嘴巴”张得——小。

师：你们三角尺上的这个角和老师大三角尺上的这个角比，谁的大？

生：肯定是老师的这个角大。

生：也有可能一样大。

师：有没有好方法来证明自己的想法？

生：放在一起，比一比。

师：请你来比给大家看！

生：一样大！

师：动手比一比，可以验证我们的猜想。为什么老师三角尺上的这个角看起来大呢？

生：老师三角尺上的角，边比较长，看上去就感觉大一些！

生：我知道了，角的大小和边长没有关系。

师：那角的大小与什么有关系呢？（停顿，观察陷入思考的学生，学生回答似乎有些困难）

师：我们再来看看，（举起张开一点角度的剪刀）剪刀上有角吗？

生：有角。

师：请仔细观察，剪刀慢慢张开，角——越来越大；剪刀慢慢收拢，角——越来越小。（学生观察教师的演示，自然地说出了结论）

师：角的大小和什么有关系呢？

生：角的大小和它张开的大小有关系！

小结：角的大小和边长没有关系，和角张开的大小有关系。

【设计意图：直角是所有角中最特别的一个，学生借助于直角模型，对数学书封面上的角进行大小判断，掌握了比较角大小的方法。他们带着直角模型，辨认其他的角是否为直角，是小于还是大于直角。充足的操作活动，为学生建立了丰富的直角、钝角、锐角的表象，将来对于这些角的命名就会水到渠成。“角的大小与什么有关系”这是个认知难点，因为学生的已有经验是根据边的长短来判定角的大小（一维的角度），或者根据角这个图形所包含的“面积大小”（二维的角度）来判定角的大小。而判断角的大小，学生必须跳出已有的经验，跳出一维和二维的角度，进行认知的重组。为了突破难点，我们分为三个层次：首先借助直角模型判断角的大小，为角的大小与边长没有关系埋下伏笔；其次，判断学生手中的尺与教师的尺上角的大小活动，再次聚焦角的大小与边长没有关系；最后，在剪刀张开、收拢，角变大、变小的过程中，学生明确了角的大小与它张开的程度有关系。在学生寻找角的活动中，还发现长方形、正方形有四个直角，这为以后观察研究图形的特征进行铺垫，让学生观察图形时多了一个角度，由点及面，从局部到整体，更加深刻和全面。】

三、抽象模型，认识角

1.认识角。

出示实物图，从中抽象出角的图形。

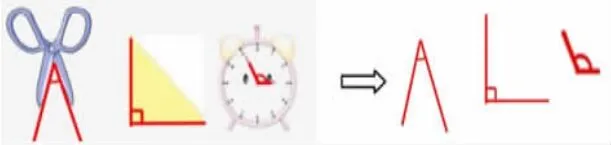
师：观察这三个角，你发现它们有什么相同的地方？

生：角有一个顶点，两条边。

师：它们有什么不同的地方？

生：角的大小不同。

师：哪个角最大？哪个角最小？

生：第三个角最大，第一个角最小。

师：怎么比较的呢？

生：第二个角是直角，第一个角比直角小，第三个角比直角大！

师：怎么看出来第三个角比直角大的呢？

生：把这两个角放在一起进行比较，顶点和顶点重合，一条边重合，看另外一条边。（电脑动画展示，图 1）

师：第三个角的边长太短，不太容易看清楚怎么办？

生：可以把第三个角的边长画长一些。（电脑动画展示，图2）

师：为了比较的方便，我们可以延长角的边长，角的边可以从顶点出发，向另一端无限延长。

图1

图2

2.画角。

师：你会用直尺画角吗？试试看！（展示学生作品略）

师：说说你是怎么画的？

生：我是沿着直角模型的顶点和边来描的。

生：我用尺画了两条边，靠在一起就可以了。

师：大家评价一下，他画得怎么样？

生：他画的顶点不是尖尖的，有些秃了！

生：他画得边不直。

师：同学们都观察得仔细，说得很好。

师：（示范角的画法）你们能画出不同类型的角吗？

生：我画出了三种类型的角，有直角，有比直角大的角，还有比直角小的角。

3.判断。

下面的图形是不是角？

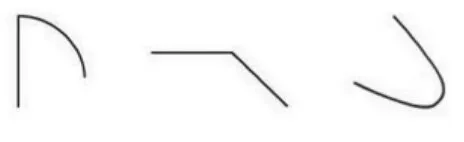
生：第一幅图不是角，因为一条边不直。

生：第二幅图是角。

生：第三幅图不是角，因为它没有顶点。

师：同学们能根据角各个部分的特征去判断，非常好！

4.数角。

数一数图形中共有多少个角？

师：第一幅图有几个角？

生：三个。

生：不对，是一个，上面的边不直。

师：第四幅图呢？

生：两个。

生：不对，是三个。

师：请你上来指给其他同学看一看。

总结：今天这节课我们学到了什么？你有什么收获？

【设计意图：根据低年级学生的年龄特点和认知规律，充分运用电教手段，从实物抽象出角，形象直观。在观察抽象出来的角时，我们特别安排了边长、位置、方向、大小不同的三个角，让学生找一找相同点和不同点。学生在找相同点时，找到了“角有一个顶点两条边”，找不同点时，发现了角的大小不同，尤其是边长最短的这个角，还是最大的角，通过动画展示，让学生直观理解角的边可以从顶点开始，向另一端无限延长！充分利用变式，排除非本质属性的干扰。学生掌握了角的本质，完成了从感性认识到理性认识的飞跃。在画角环节，我们增加了难度，要求画出不同的角来，很多学生都能自己尝试画出直角、钝角、锐角；判断角和数角的练习，抓住了对角的本质属性，锻炼和提升了学生的思维能力。这些练习的设计，要求逐渐提高，使学生能够把习得的概念最终转化为技能。】