垄沟集雨系统Laio土壤水分动态随机模型参数敏感性分析及优化*
2018-05-10尹鑫卫李晓玲张永梅
尹鑫卫, 李晓玲, 王 琦, 张永梅
垄沟集雨系统Laio土壤水分动态随机模型参数敏感性分析及优化*
尹鑫卫1,2, 李晓玲3, 王 琦4**, 张永梅1,2
(1. 中国科学院新疆生态与地理研究所/阜康荒漠生态国家野外科学观测研究站 乌鲁木齐 830011; 2. 中国科学院大学 北京 100049; 3. 甘肃农业大学水利水电工程学院 兰州 730070; 4. 甘肃农业大学草业学院 兰州 730070)
水文模型参数的敏感性分析、优化和验证对提高模型计算精度和效率具有重要意义。为探讨Laio土壤水分动态随机模型(Laio模型)各参数在垄沟集雨系统的敏感性, 同时, 确定参数优化和模型验证的最佳方案, 本文结合多因素敏感性分析法以及改进单纯形法(ISM)、粒子群优化算法(PSO)和混合粒子群优化算法(HPSO), 利用中国气象局定西干旱气象与生态环境试验基地2012—2013年垄沟集雨燕麦生长季降雨、径流和土壤水分等实测数据, 对垄沟集雨系统Laio模型的13个参数进行敏感性分析、优化和验证。结果表明, 平均降水量和凋萎系数w对土壤水分概率密度函数(s)最敏感,(s)对参数的敏感性在低土壤含水率下更明显, 对参数w的敏感性在高土壤含水率下更明显; 3种算法(ISM、PSO和HPSO)的优化参数值均能对垄沟集雨系统土壤水分概率密度函数进行较好模拟, 峰值(CPV)、峰值位置(PP)和95%置信区间(CI95%)实测值与模拟值的相对误差均小于10%, CM指数均大于0.5; 同时, HPSO算法优化参数的模拟效果和收敛速度均显著优于PSO算法和ISM算法, 能较显著克服ISM算法和PSO算法存在的缺陷。HPSO算法可作为垄沟集雨系统土壤水分动态随机模型参数优化的待选方案。
垄沟集雨系统; 土壤水分动态; Laio土壤水分动态随机模型; 敏感性分析; 模型参数优化
水资源短缺是全球旱地农业面临的共同难题。如何充分利用天然降雨资源、确保粮食生产安全和维持农田生态系统稳定是实现旱农区“农业-生态-经济”耦合系统协调、持续发展的关键[1]。同时, 研发和推广高效、低廉、环保的旱作栽培技术对提高旱农区作物产量及水分利用效率具有重要的意义[2]。垄沟集雨系统利用田间起垄、沟垄相间、垄面产流、沟内高效集雨, 并依靠增温、抑蒸、保土等生理生态效应, 已成为水分缺乏的半干旱区农田生态系统一项重要的集水节灌措施[3-4]。其在缓解旱农区人口急剧增长、粮食日益紧缺与农业生态恶化的矛盾中发挥着至关重要的作用。
土壤水分是半干旱农田生态系统植物水分的主要来源, 是养分循环和流动的载体, 在土壤-植被-大气系统物质和能量转化中起着核心和纽带的重要作用[5]。认识半干旱农田生态系统与土壤水分关系和相互作用机理, 对揭示农田生态系统稳定性及其水土关键要素的变化过程具有重要意义[6]。由于影响土壤水分动态的各因素(降水、蒸散发、土壤异质性、地形等)具有随机性, 特别是降雨事件发生及降雨量分布的随机性, 决定了土壤水分动态模型只有以概率形式描述才更具有实际意义[7]。自Eagleson等[8]首次将随机理念纳入土壤水量平衡方程, Milly[9]、Rodriguez-Iturbe等[10]、Laio等[11]、Porporato等[12]、Pan等[13]先后对不同时空尺度的土壤水分动态建立了随机数学模型, 并得到广泛应用。Laio土壤水分动态随机模型(Laio模型)在蒸散发项上引进了2个土壤水分临界值(凋萎系数和吸湿系数), 能对干旱半干旱区农田生态系统土壤水分动态进行更真实地描述, 可为旱农区土壤水分的有效利用与管理提供理论指导。
由于半干旱区垄沟集雨系统土壤水分与多种物理、化学和生物过程以及降雨、径流、蒸散发、土壤特性、微地形及覆盖材料等密切相关, 长期处于动态变化状态, 且变化过程比较复杂[14-16], 所以利用Laio模型对该系统土壤水分动态进行模拟和研究是很有必要的。Laio模型共涉及土壤、植被和气候等13个参数, 部分参数很难通过观测直接获取, 且参数值存在极大不确定性[17-18]。故在模型应用前需考虑模型“本地化”和“区域化”问题, 即需对模型参数进行敏感性分析和优化。目前针对Laio模型参数敏感性及获取方法已有相关研究, 如姚淑霞等[7]在科尔沁沙地对Laio模型参数敏感性进行了分析, 并将参数按敏感性强弱分为了3类; Milly等[9]对Laio模型参数的获取及敏感性分析发现, 最大蒸散量(max)和水分胁迫点(*)最难获取, 且敏感性也最强; 任庆福[17]利用PSO算法对太行山山前平原典型井灌农区Laio模型参数进行了优化, 发现经率定的参数能更好地模拟作物生长期土壤水分的随机变化特征。然而, 对不同含水率条件下垄沟集雨系统Laio模型参数的敏感性, 以及各种优化算法对模型参数优化的适应度和有效性尚缺乏系统研究。鉴此, 建立方便可行的垄沟集雨系统Laio模型参数优化、敏感性分析和有效性验证的方法体系对提高参数率定效率, 控制模型计算误差和拓宽模型应用领域具有极其重要的意义。
本文利用中国气象局定西干旱气象与生态环境试验基地2012—2013年垄沟集雨燕麦()生长季降雨、径流和土壤水分等实测数据资料, 采用多因素敏感性分析法, 对半干旱区垄沟集雨系统Laio土壤水分动态随机模型参数敏感性进行分析和分类。同时, 基于ISM、PSO和HPSO算法, 对垄沟集雨系统Laio模型的13个参数进行优化和优选, 并利用实测数据资料对3种算法优化参数的有效性进行验证和评价, 以期建立垄沟集雨系统Laio模型参数敏感性分析、优化和验证的有效方法体系, 为Laio模型参数校正和区域应用提供科学理论依据。
1 材料与方法
1.1 田间试验和数据测定
试验于2012—2013年在中国气象局兰州干旱气象研究所定西干旱气象与生态环境试验基地(35°33′N, 104°35′E, 海拔1 896.7 m)进行, 该基地属黄土高原西部丘陵区和半干旱地区, 具有典型的温带大陆性季风气候[16]。1971—2014年平均降雨量388 mm, 冬季和夏季月平均降雨量分别为20~80 mm和150~270 mm。降雨在年内分布极不均匀, 7—10月降雨量占年降雨量的86.9%, 蒸发强烈, 年均潜在蒸发量达1 500 mm。试验地地势平坦, 土壤为重壤土, 0~100 cm土壤平均容重为1.38 g·cm-3, 田间持水量为25.60%, 饱和含水量为43.87%, 永久凋萎系数为6.70%, 地下水埋深10.4 m, 土壤水与地下水的水力联系微弱。当地耕作制度为一年1熟, 主要种植作物有春小麦()、燕麦和马铃薯()等, 主要种植牧草有紫花苜蓿()和红豆草()等。
试验采用田间垄沟集雨覆盖种植技术, 以燕麦为指示作物, 垄覆盖作为集雨区, 沟无覆盖作为种植区, 小区随机排列, 共设9个处理(3种沟垄比×3种覆盖材料), 重复3次。3种覆盖材料分别为生物可降解膜、普通塑料膜和土壤结皮, 3种沟垄比分别为60 cm︰30 cm、60 cm︰45 cm和60 cm︰60 cm(沟宽︰垄宽)。生物可降解地膜和普通塑料膜厚度均为0.08 mm; 土垄为人工原土夯实, 经风吹雨打形成自然土壤结皮。土垄、生物可降解地膜垄和普通地膜垄的代表符号分别为SR、BMR和CMR。根据当地种植经验, 集雨垄的坡度为40°, 高为25 cm, 长为10 m, 每1小区有4条垄和3条沟。试验设计见表1,种植示意图见图1。相关种植管理方法按前期研究者[19]所述进行。由于本试验3种沟垄比对该系统土壤水分时空动态影响不显著[16-19], 故本文土壤含水量均为同一覆盖材料下, 3种试验沟垄比之均值。
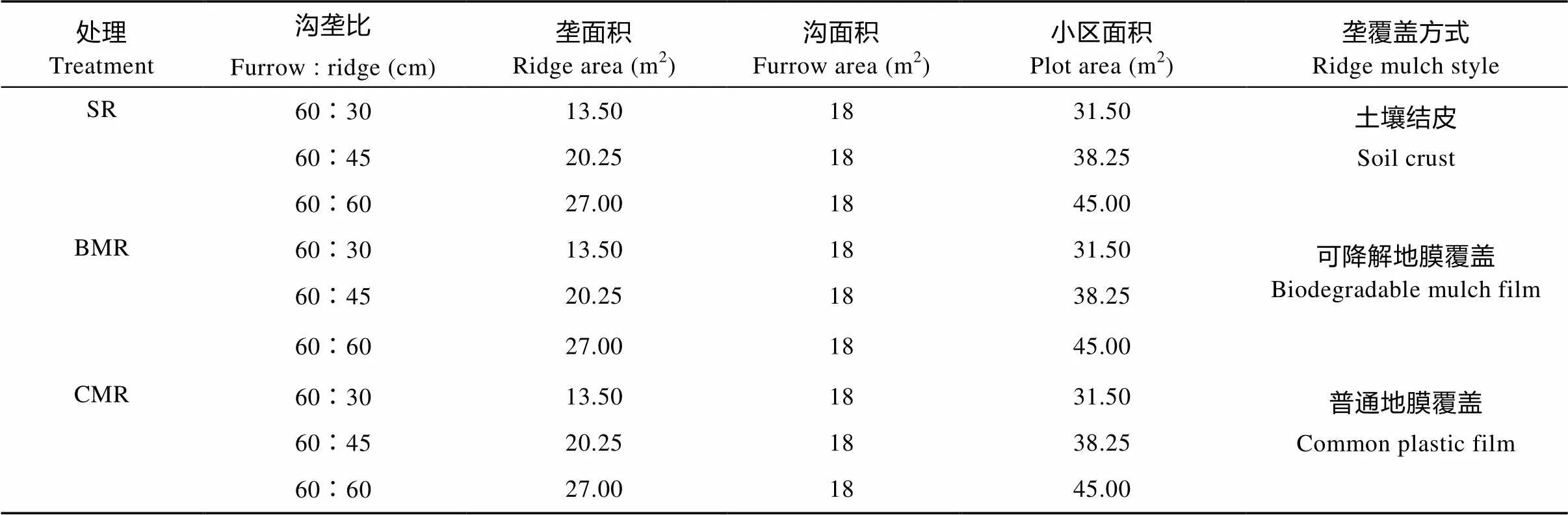
表1 垄沟集雨种植燕麦试验设计
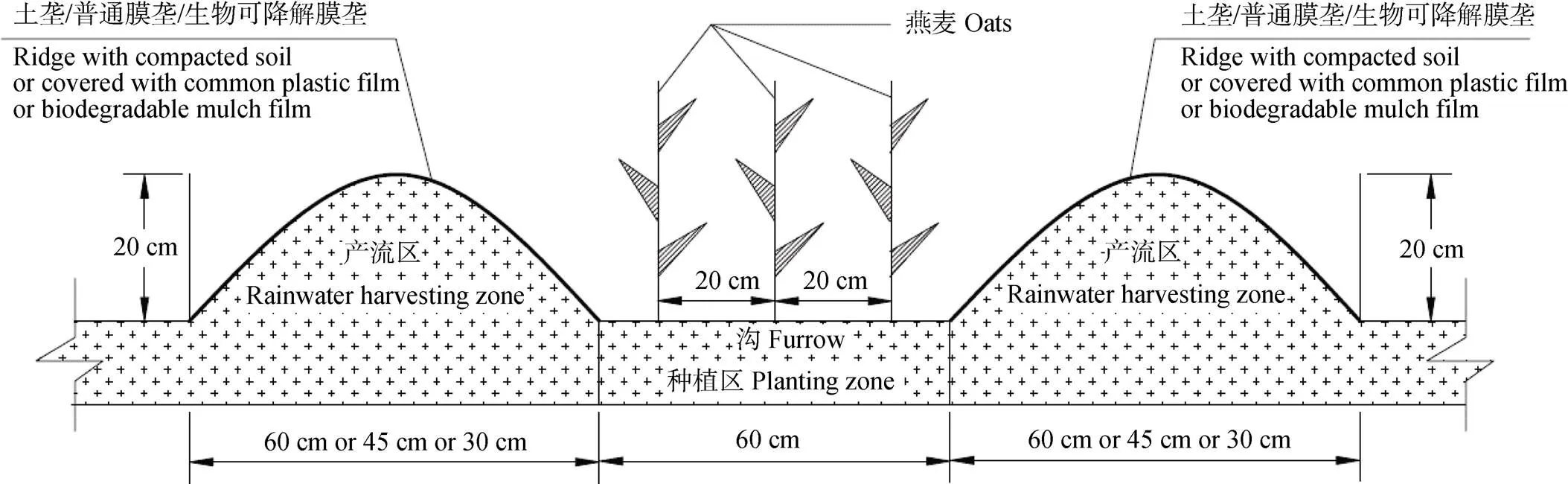
图1 垄沟集雨种植燕麦示意图
试验期降雨量数据由试验基地自记雨量计测定。土壤含水量采用烘干法(105 ℃, 10 h)于燕麦播种前(4月10日左右)、收获后(8月20日左右)和降雨后(降雨量>5 mm)测定, 测定深度140 cm, 分层深度为20 cm, 共记录7个土层的土壤含水量, 每1小区随机在沟内选取3个样点, 同一层次土壤含水量取3个样点平均值。集雨垄径流量由降雨量数据基于美国水土保持局研制的SCS-CN模型反推确定[20]。土壤容重采用环刀法测定, 测定深度140 cm, 分层深度为20 cm, 每层3个重复, 取均值。根系层深度通过实地调查燕麦根系生物量分布范围测定[7]。同期气象数据由邻近的试验基地气象观测站获得。
1.2 Laio土壤水分动态随机模型
土壤水分随机模型的理论基础是物质平衡原理: 单位时间内土壤含水量的变化等于土壤水分输入项和水分损失项的差。基于前期研究者[21]对土壤水分随机模型的研究, Laio等[11]通过引进两个临界土壤含水量(土壤吸湿系数和土壤凋萎系数), 在空间一点上建立了时间尺度为1 d的土壤水分平衡方程, 具体模型(Laio模型)可表述为:
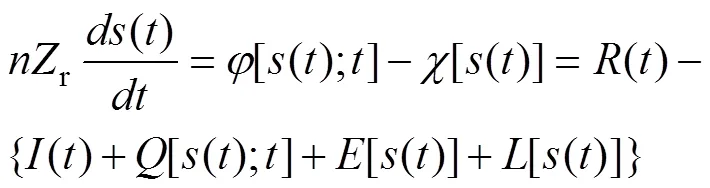
将降雨随机过程同土壤水分损失项(土壤水蒸散发与深层渗漏之和)相结合是土壤水分随机模型建立的基础[21-22]。由于降雨是随机过程, 故需建立土壤水分概率密度函数求解土壤水平衡过程(公式1)。通过将Laio模型的各土壤水分损失过程转化为查普曼-柯尔莫哥洛夫前进方程(Chapman- Kolmogorov Forward Function)可分析求解导出土壤水分概率密度函数, 其具体表达式[7,11,21-22]为:


表2 垄沟集雨系统Laio模型参数取值范围及其不同覆盖处理的初始值
表中模型参数取值范围由相关实测数据和文献资料[11,16]获得。UBV: 参数取值下限; LBV: 参数取值上限。Values ranges of model parameters in the table were obtained from the relevant measured data and literatures[11,16]. UBV: upper bound value of model parameter; LBV: lower bound value of model parameter.
1.3 模型参数敏感性分析原理
模型参数的敏感性分析是研究参数变化所引起的模型响应, 是模型参数不确定分析的重要内容之一, 也是研发和评价模型不可缺少的重要环节[23]。同时, 参数敏感性分析有助于深入理解模型的特性并改进模型结构的稳定性[24]。为不失一般性, 可将土壤水分概率密度函数表示为:
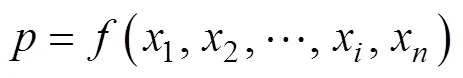
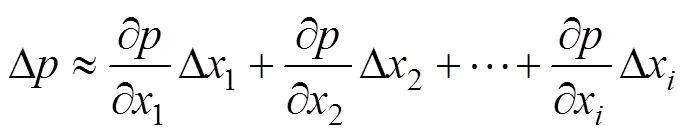
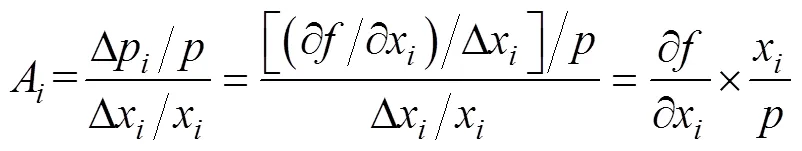
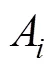
1.4 模型参数优化算法原理
1.4.1 改进单纯形法寻优原理
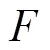
1.4.2 粒子群优化算法寻优原理
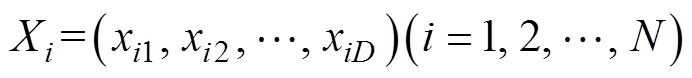
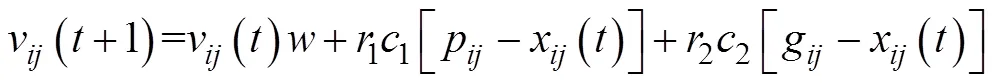
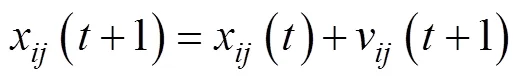
1.4.3 混合粒子群优算法寻优原理
为提高优化算法在全局和局部意义下的搜索能力和收敛效率, 以粒子群优算法流程为基础, 引入改进单纯形搜索方法构成混合粒子群优算法(Hybrid Particle Swarm Optimization, HPSO)[29], 即在每1次迭代中先用PSO算法对群体进行全局寻优, 然后通过ISM算法对粒子群中部分精英粒子在其较优解领域内进行局部搜索, 寻找更优解。
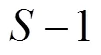
1.5 Laio模型转换与参数优化
1.6 模型的验证与评价方法
通过比较研究区不同处理实测土壤水分概率密度函数曲线与ISM、PSO和HPSO算法优化参数值模拟曲线的特征, 评价以上3种算法对Laio模型参数优化的有效性。验证评价指标选择CM(Consistency Measure)指数[32], 其表示两目标曲线的一致性程度, 计算方法如下:
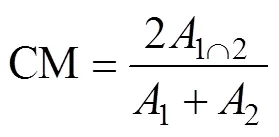
式中: 表示目标曲线1下方的面积, 表示目标曲线2下方的面积, 表示目标曲线1和目标曲线2下方的公共面积(图2a, b, c)。显然, 目标曲线1与目标曲线2一致性越好, 越大, CM指数越大; 反之, 一致性越差, 越小, CM指数越小。CM指数的变化范围为[0, 1], 当CM=1时, 表明目标曲线1和目标曲线2一致性最佳; 当CM=0时, 表明目标曲线1和目标曲线2之间不存在一致性(见图2d, e)。
2 结果与分析
2.1 Laio模型参数敏感性分析

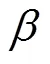
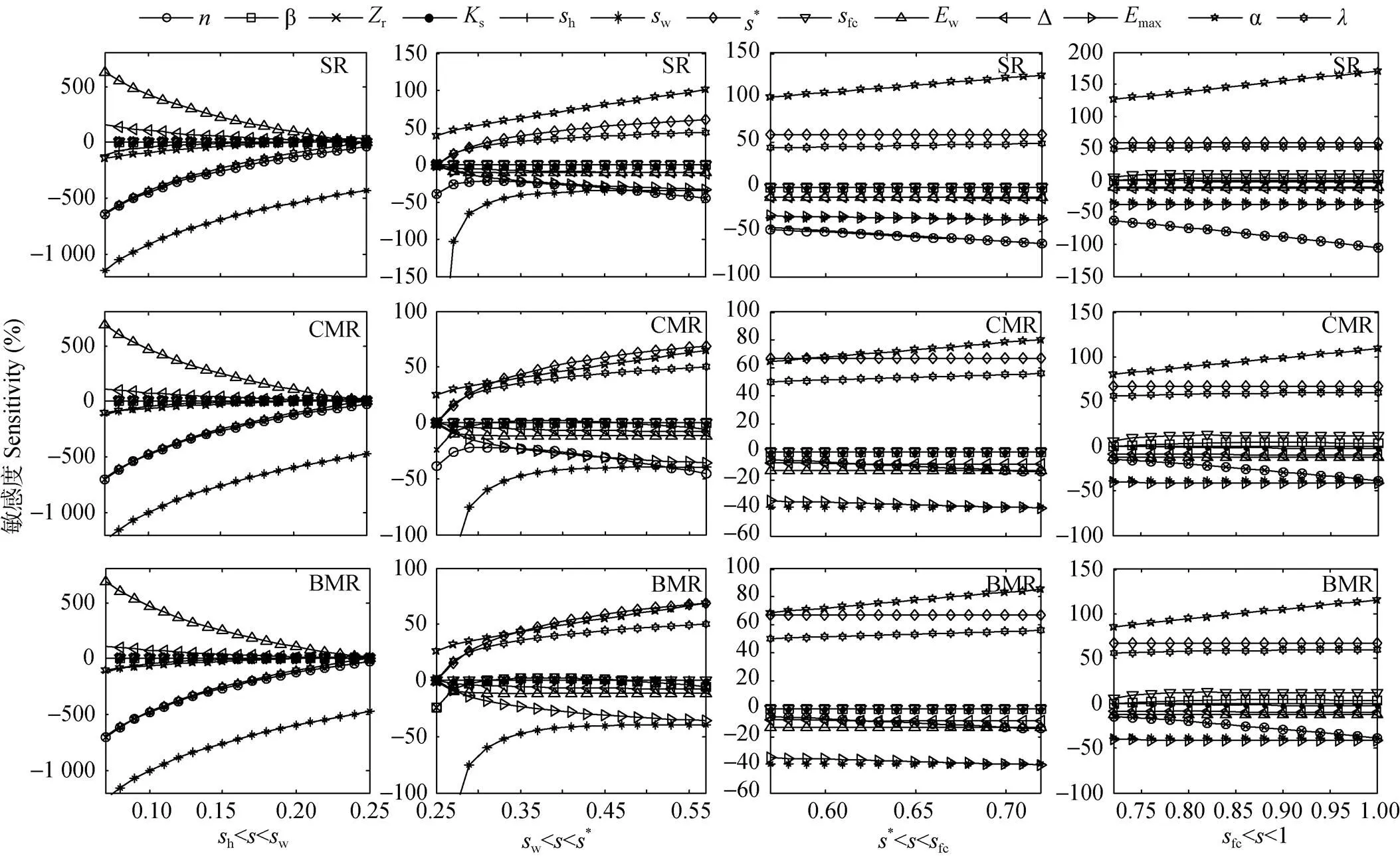
图3 不同土壤含水率下不同覆盖处理的垄沟集雨系统Laio模型各参数敏感性分析
模型参数的意义见表2。Meanings of parameters are shown in the table 2.
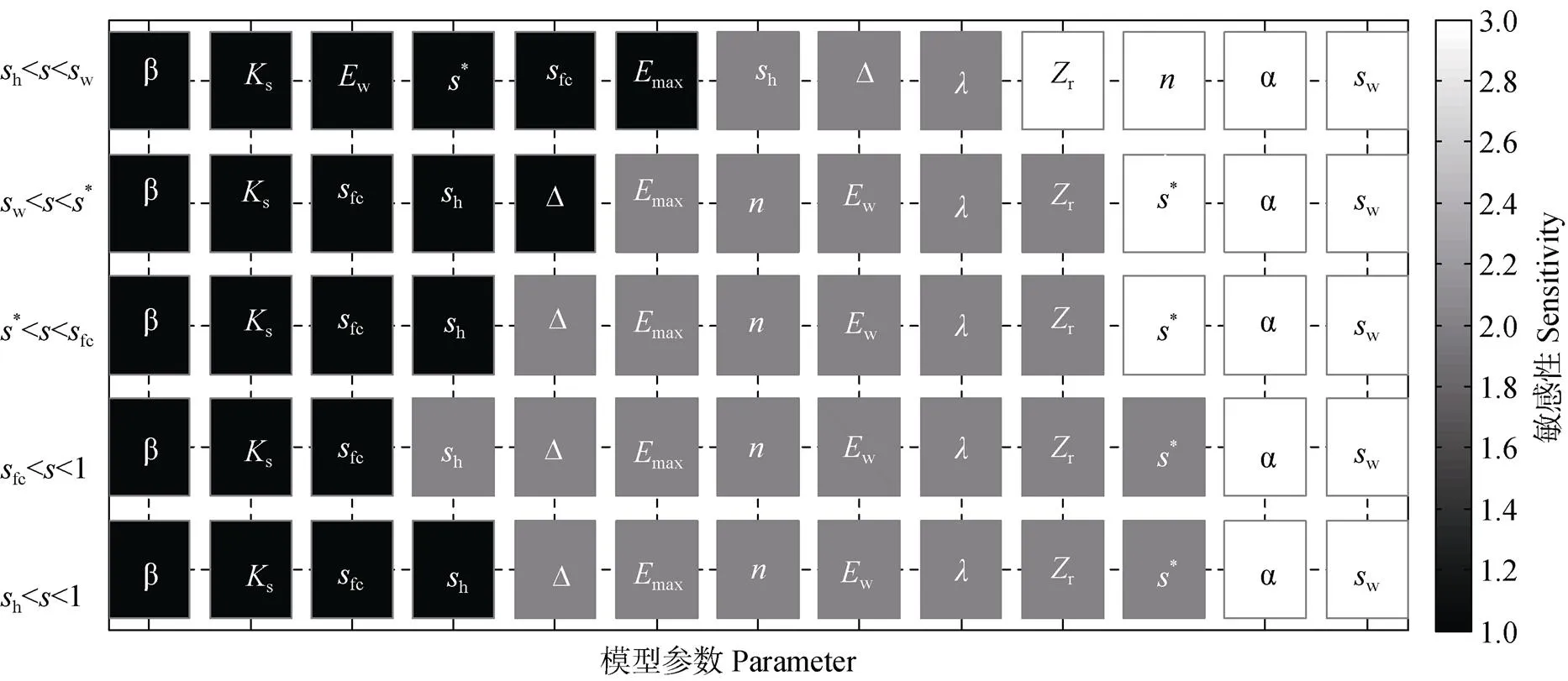
图4 基于SOM神经网络聚类法的垄沟集雨系统Laio模型参数敏感性分类
模型参数的意义见表2。Meanings of parameters are shown in the table 2.
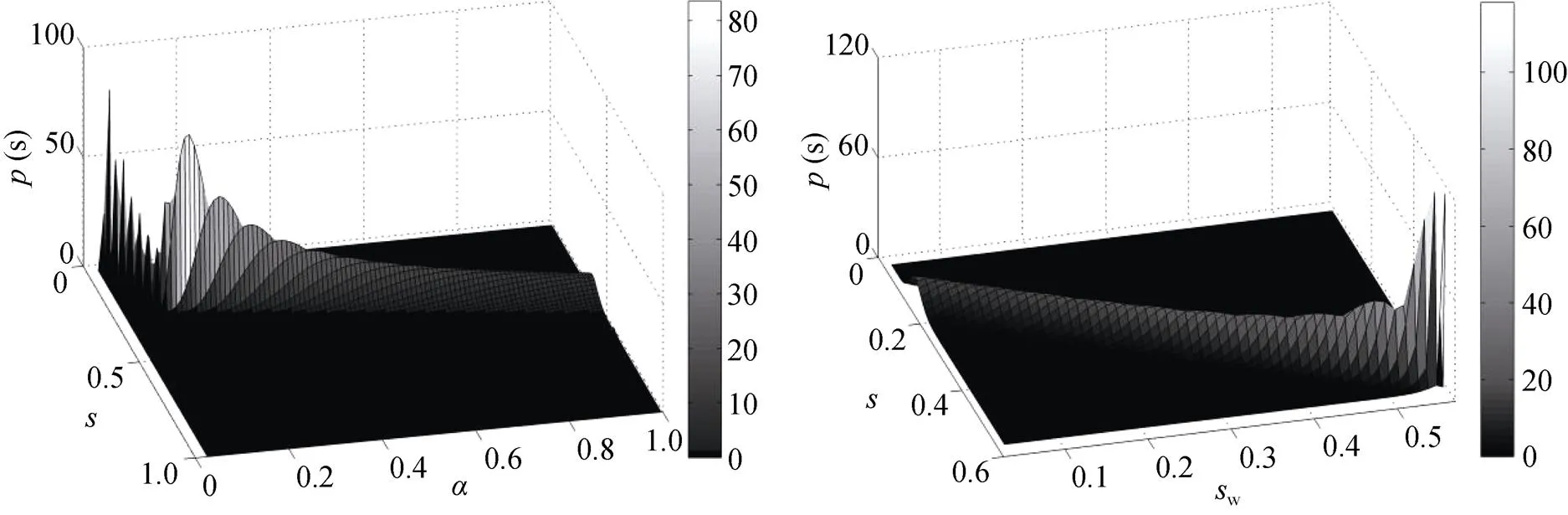
图5 参数α(生长季平均降水量)和sw(凋萎系数)对垄沟集雨系统土壤水分概率密度函数[p(s)]的影响
2.2 基于ISM、PSO和HPSO算法的模型参数优化
为确保算法的优化精度和有效性, 当算法运行过程中符合下列3个终止准则之一时停止计算[35]。准则1: 两次迭代的最优目标函数值对应的参数距离小于给定精度1≤10-5; 准则2: 两次迭代的目标函数值之差小于给定精度2≤10-5; 准则3: 循环的最大次数已达到。同时, 为尽可能消除算法随机性对各算法比较的影响, 每个优化算法均随机独立运行10次后取各参数平均最优解和计算效率。算法运行结果和优化参数验证见表3及图6所示。
从3种优化算法(ISM、PSO和HPSO)对Laio模型参数优化结果(表3)和优化效率(图6)可看出, ISM算法优化参数的有效性明显低于另外两种算法, 其对模型参数初始值依赖性较强, 如果不事先用具有较强全局寻优能力的算法获取一组较优初始值, 其优化结果将易陷入局部最优。PSO算法具有较强的全局寻优能力, 优化参数的有效性较强, 但其在算法迭代后期收敛速度相对较慢, 存在有早熟、局部收敛等缺陷。HPSO算法优化参数的有效性明显优于ISM算法和PSO算法的优化解, 其不但具有较强的全局搜索能力, 而且具有较快的收敛速度, 能较显著地克服ISM算法和PSO算法相互存在的缺陷。这与陈俊风等[29]对HPSO算法的仿真实验结论相一致, 说明其有利于增强全局和局部意义下优化结果的可靠性和算法的优化性能, 是求解优化问题的一种有效的算法。
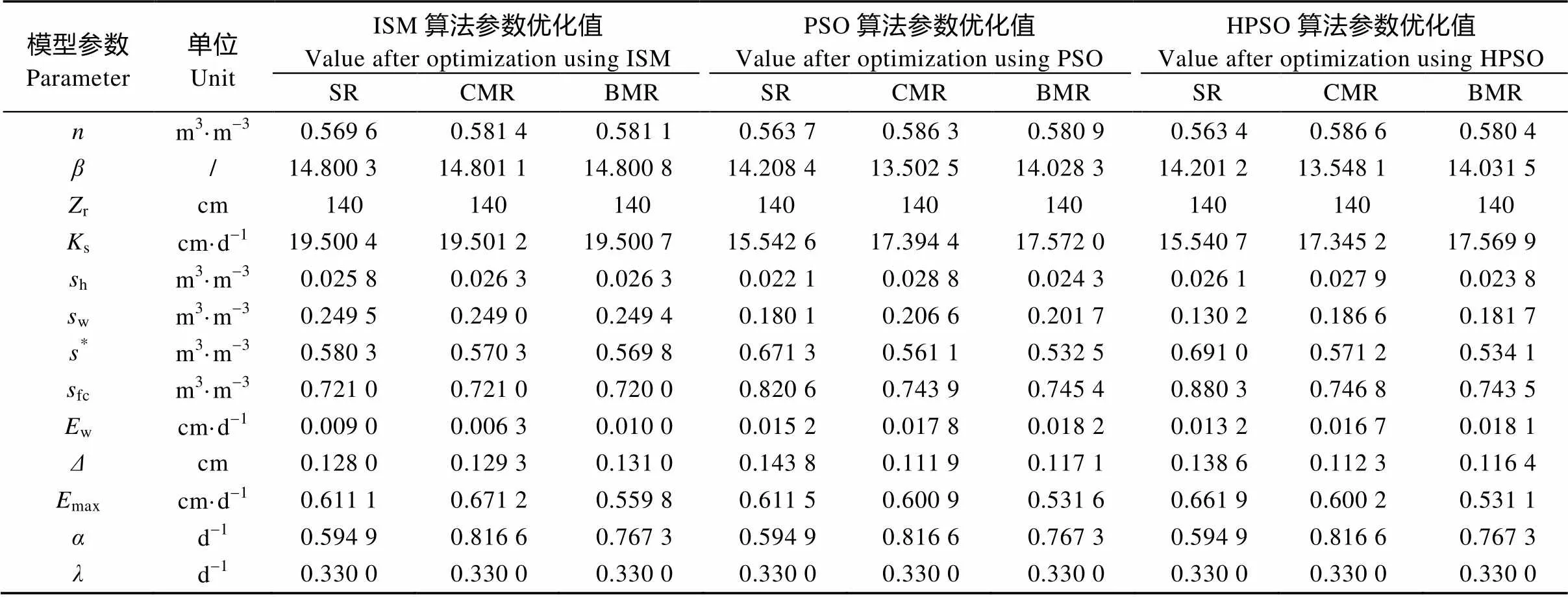
表3 基于ISM、PSO和HPSO算法的垄沟集雨系统Laio模型参数优化结果
模型参数的意义见表2。Meanings of parameters are shown in the table 2.
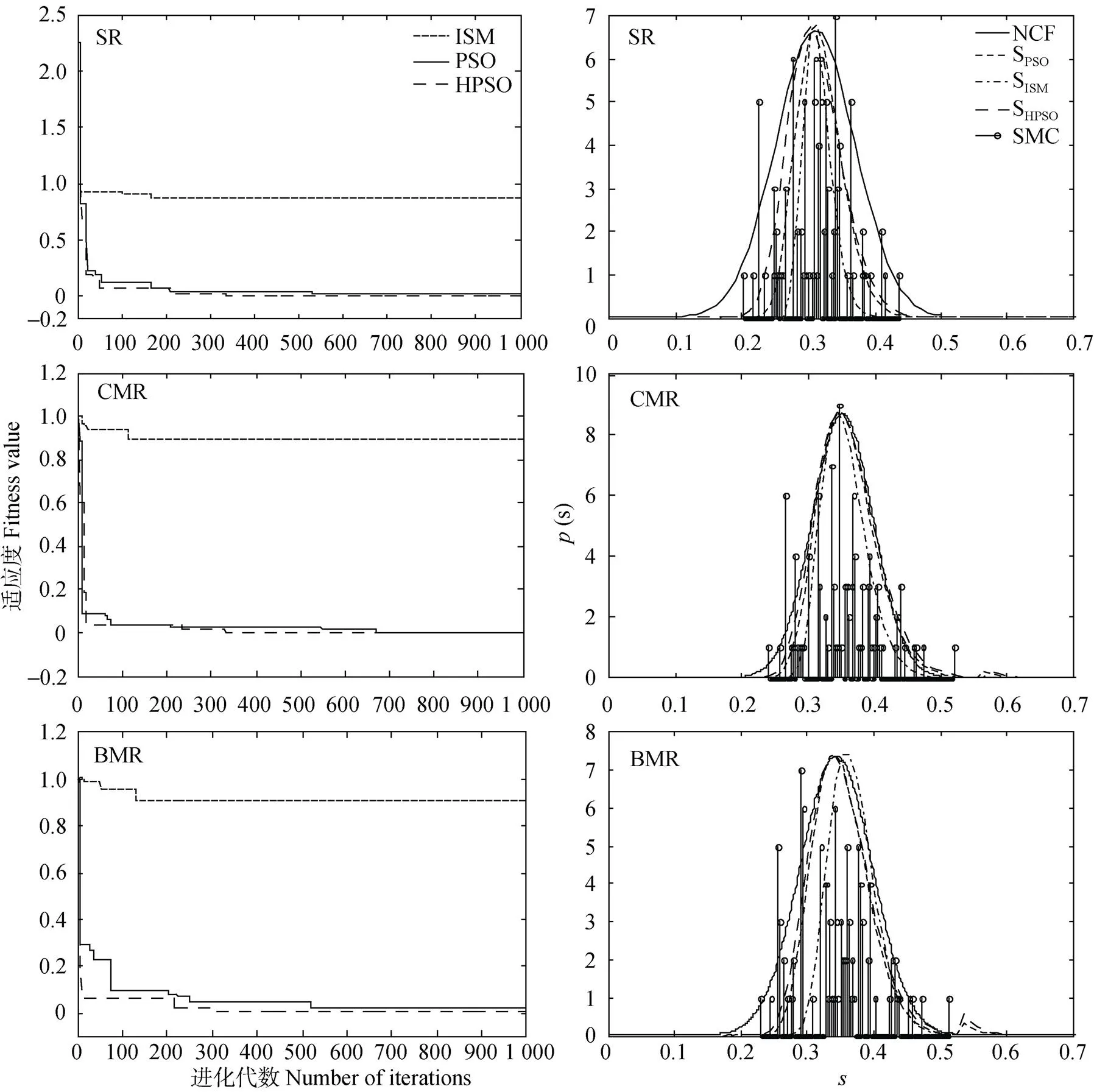
图6 基于ISM、PSO和HPSO算法的垄沟集雨系统Laio模型参数优化效率和有效性验证
SMC: 土壤含水量; NCF: 正态曲线拟合; SPSO: PSO优化参数模拟曲线; SISM: ISM优化参数模拟曲线; SHPSO: HPSO优化参数模拟曲线。SMC: soil moisture content; NCF: normal curve fitting; SPSO: simulating curves with PSO-optimized parameters; SISM: simulating curves with ISM-optimized; SHPSO: simulating curves with HPSO-optimized parameters.
2.3 模型参数有效性验证与评价
采用试验区2012—2013年田间垄沟集雨系统各处理(SR、CMR和BMR)降雨、径流、土壤含水率等实测数据资料, 基于3种算法(ISM、PSO和HPSO)对Laio模型参数优化值, 比较模型模拟与实测的土壤水分概率密度函数在曲线形状[峰值、峰值出现的位置, 95%置信区间(CI95%)]和CM指数之间的匹配程度, 评价3种算法对Laio模型参数优化的有效性, 选择较优模型参数优化值及参数优选算法类型。图6和表4为3种算法的垄沟集雨系统Laio模型优化参数有效性验证与评价结果。

表4 基于ISM、PSO和HPSO算法的垄沟集雨系统Laio模型参数优化性能比较
CPV: 峰值; PP: 峰值位置; CI95%: 95%置信区间; CM: 一致性指数。CPV: the curve peak value; PP: the position of the peak; CI95%: the confidence interval of 95%; CM: the consistency measure.
从图6和表4可看出, 3种算法优化模型参数值均能比较准确地描绘出曲线的形状, 捕捉到峰值的位置, 描述出土壤水分概率密度函数的主要特征, 且CPV、PP和CI95%实测值与模拟值相对误差均小于10%, CM指数均大于0.5, 说明3种算法优化参数值对垄沟集雨系统土壤水分概率密度函数模拟效果较好。同时, HPSO算法优化参数的模拟效果(CM指数均值为0.901)优于PSO算法(CM指数均值为0.848), PSO算法优于ISM算法(CM指数均值为0.678), 且HPSO算法优化参数的收敛速度(进化代数均值为285)均快于PSO算法(进化代数均值为503), 说明HPSO算法优化模型参数值可较显著提高垄沟集雨系统土壤水分概率密度模拟精度和效率,故HPSO算法可作为该系统土壤水分动态随机模型参数优选的较优待选方案。但是, 相关研究表明[36], 全局算法与局部算法相混合得到的混合优化算法,尽管可以提高局部收敛速度和性能, 但也加剧了陷入局部极小的可能。因此, 构建能显著提高局部搜索能力, 且能高概率搜索全局最优解的混合优化算法, 有待进一步深入的研究。
3 结论
本文采用多因素敏感性分析法, 对半干旱区垄沟集雨系统Laio土壤水分动态随机模型参数的敏感性进行了分析和分类。同时, 基于3种优化算法(ISM、PSO和HPSO), 对垄沟集雨系统Laio模型的13个参数进行了优化和优选, 并利用实测数据资料对3种算法优化参数的有效性进行了验证和评价。得到的主要结论如下:
3)3种算法的优化参数值均能较好地模拟垄沟集雨系统土壤水分概率密度函数, 各处理的CPV、PP和CI95%实测值与模拟值相对误差均小于10%, CM指数均大于0.5。
4)HPSO算法优化参数的模拟效果和收敛速度均显著优于PSO算法和ISM算法, 且能较显著克服ISM算法和PSO算法存在的缺陷, HPSO算法可作为垄沟集雨系统土壤水分动态随机模型参数优选的较优待选方案。
[1] 莫非, 周宏, 王建永, 等. 田间微集雨技术研究及应用[J]. 农业工程学报, 2013, 29(8): 1–17 MO F, ZHOU H, WANG J Y, et al. Development and application of micro-field rain-harvesting technologies[J]. Transactions of the CSAE, 2013, 29(8): 1–17
[2] ZHOU L M, ZHANG F, LIU C A. Improved yield by harvesting water with ridges and subgrooves using buried and surface plastic mulchs in a semiarid area of China[J]. Soil and Tillage Research, 2015, 150: 21–29
[3] DU Y J, LI Z Z, LI W L. Effect of different water supply regimes on growth and size hierarchy in spring wheat populations under mulched with clear plastic film[J]. Agricultural Water Management, 2006, 79(3): 265–279
[4] JIA Y, LI F M, WANG X L. Soil quality responses to alfalfa watered with a field micro-catchment technique in the Loess Plateau of China[J]. Field Crops Research, 2006, 95(1): 64–74
[5] 李小雁. 干旱地区土壤-植被-水文耦合、响应与适应机制[J]. 中国科学: 地球科学, 2011, 41(12): 1721–1730 LI X Y. Mechanism of coupling, response and adaptation between soil, vegetation and hydrology in arid and semiarid regions[J]. Scientia Sinica Terrae, 2011, 41(12): 1721–1730
[6] PORPORATO A, FENG X, MANZONI S, et al. Ecohydrological modeling in agroecosystems: Examples and challenges[J]. Water Resources Research, 2015, 51(7): 5081–5099
[7] 姚淑霞, 张铜会, 赵传成. 科尔沁沙地土壤水分动态分析及其概率密度函数模拟[J]. 水科学进展, 2013, 24(1): 62–72YAO S X, ZHANG T H, ZHAO C C. Analysis of soil moisture dynamics and its probability density function simulation in Horqin Sand Land[J]. Advances in Water Science, 2013, 24(1): 62–72
[8] EAGLESON P S. Climate, soil, and vegetation: 1. Introduction to water balance dynamics[J]. Water Resources Research, 1978, 14(5): 705–712
[9] MILLY P C D. An analytic solution of the stochastic storage problem applicable to soil water[J]. Water Resources Research, 1993, 29(11): 3755–3758
[10] RODRIGUEZ-ITURBE I, PORPORATO A, RIDOLFI L, et al. Probabilistic modelling of water balance at a point: The role of climate, soil and vegetation[J]. Proceedings of the Royal of Society A, 1999, 455(1990): 3789–3805
[11] LAIO F, PORPORATO A, RIDOLFI L, et al. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: Ⅱ. Probabilistic soil moisture dynamics[J]. Advances in Water Resources, 2001, 24(7): 707–723
[12] PORPORATO A, DALY E, RODRIGUEZ-ITURBE I. Soil water balance and ecosystem response to climate change[J]. The American Naturalist, 2004, 164 (5): 625–632
[13] PAN X Y, POTTER N J, XIA J, et al. Hillslope-scale probabilistic characterization of soil moisture dynamics and average water balance[J]. Hydrological Processes, 2013, 27(10): 1464–1474
[14] BEN-ASHER J, WARRICK A W. Effect of variations in soil properties and precipitation on microcatchment water balance[J]. Agricultural Water Management, 1987, 12(3): 177–194
[15] LI X Y, SHI P J, SUN Y L, et al. Influence of various in situ rainwater harvesting methods on soil moisture and growth ofin the semiarid loess region of China[J]. Forest Ecology and Management, 2006, 233(1): 143–148
[16] WANG Q, REN X, SONG X Y, et al. The optimum ridge-furrow ratio and suitable ridge-covering material in rainwater harvesting for oats production in semiarid regions of China[J]. Field Crops Research, 2015, 172: 106–118
[17] 任庆福. 气候变化下典型农田土壤水分随机模拟及应用[D].北京: 北京林业大学, 2016: 83–94 REN Q F. Stochastic simulation for the typical farmland soil moisture under climate change and its application to the Shijin irrigated district in Hebei Province[D]. Beijing: Beijing Forestry University, 2016: 83–94
[18] MILLER G R, BALDOCCHI D D, LAW B E, et al. An analysis of soil moisture dynamics using multi-year data from a network of micrometeorological observation sites[J]. Advances in Water Resources, 2007, 30(5): 1065–1081
[19] 任祥, 王琦, 张恩和, 等. 覆盖材料和沟垄比对燕麦产量和水分利用效率的影响[J]. 中国生态农业学报, 2014, 22(8): 945–954 REN X, WANG Q, ZHANG E H, et al. Effects of mulching materials and furrow-to-ridge ratios on oat grain/hay yield and water use efficiency under rainwater harvesting cultivation[J]. Chinese Journal of Eco-Agriculture, 2014, 22(8): 945–954
[20] 尹鑫卫, 李晓玲, 康燕霞, 等. 基于SCS-CN模型的沟垄微型集雨系统径流预测[J]. 生态学杂志, 2015, 34(12): 3502–3508 YIN X W, LI X L, KANG Y X, et al. Prediction of runoff in ridge-furrow rainwater harvesting system based on SCS-CN model[J]. Chinese Journal of Ecology, 2015, 34(12): 3502–3508
[21] 潘兴瑶, 夏军, 张橹. 土壤水分随机模型支持下的土壤水平衡研究进展[J]. 资源科学, 2008, 30(3): 460–467 PAN X Y, XIA J, ZHANG L. A review of soil water balance studies based on stochastic soil moisture model[J]. Resources Science, 2008, 30(3): 460–467
[22] 胡健, 吕一河. 土壤水分动态随机模型研究进展[J]. 地理科学进展, 2015, 34(3): 389–400 HU J, LYU Y H. Research progress on stochastic soil moisture dynamic model[J]. Progress in Geography, 2015, 34(3): 389–400
[23] VANROLLEGHEM P A, MANNINA G, COSENZA A, et al. Global sensitivity analysis for urban water quality modelling: Terminology, convergence and comparison of different methods[J]. Journal of Hydrology, 2015, 522: 339–352
[24] 李毅, 邵明安, 王文焰, 等. 土壤非饱和导水率模型中参数的敏感性分析[J]. 水科学进展, 2003, 14(5): 593–597 LI Y, SHAO M A, WANG W Y, et al. Sensitive analyses of parameters in unsaturated soil hydraulic conductivity model[J]. Advances in Water Science, 2003, 14(5): 593–597
[25] NELDER J A, MEAD R. A Simplex Method for function minimization[J]. The Computer Journal, 1965, 7(4): 308–313
[26] 刘欢培, 黄建华. 改进单纯形法寻优的MATLAB实现[J]. 浙江工业大学学报, 2003, 31(4): 377–381 LIU H P, HUANG J H. Realization of improved simplex method using MATLAB[J]. Journal of Zhejiang University of Technology, 2003, 31(4): 377–381
[27] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of 1995 IEEE International Conference on Neural Networks. Piscataway: IEEE Service Center, 1995: 1942–1948
[28] 刘苏宁, 甘泓, 魏国孝. 粒子群算法在新安江模型参数率定中的应用[J]. 水利学报, 2010, 41(5): 537–544 LIU S N, GAN H, WEI G X. Application of PSO algorithm to calibrate the Xin’anjiang Hydrological Model[J]. Shuili Xuebao, 2010, 41(5): 537–544
[29] 陈俊风, 任子武, 范新南. 一种基于改进单纯形法和粒子群算法的混合优化算法[C]//中国自动化学会控制理论专业委员会. 第25届中国控制会议论文集(中册). 哈尔滨: 哈尔滨工业大学出版社, 2006: 7–11 CHEN J F, REN Z W, FAN X N. A hybrid optimized algorithm based on improved simplex method and particle swarm optimization[C]//Technical Committee on Control Theory, Chinese Association of Automation. Proceedings of the 25th Chinese Control Conference (Middle). Harbin: Harbin Institute of Technology Press, 2006: 7–11
[30] 陆克中, 吴璞, 王汝传. 基于粒子群优化算法的非线性系统模型参数估计[J]. 计算机技术与发展, 2008, 18(6): 57–59 LU K Z, WU P, WANG R C. A method of parameter estimation in a nonlinear system model based on particle swarm optimization[J]. Computer Technology and Development, 2008, 18(6): 57–59
[31] 吴春梅. 现代智能优化算法的研究综述[J]. 科技信息, 2012, (8): 31 WU C M. A review of modern intelligent optimized algorithm[J]. Science & Technology Information, 2012, (8): 31
[32] ZHU A X. A personal construct-based knowledge acquisition process for natural resource mapping[J]. International Journal of Geographical Information Science, 1999, 13(2): 119–141
[33] 任小龙, 贾志宽, 丁瑞霞, 等. 我国旱区作物根域微集水种植技术研究进展及展望[J]. 干旱地区农业研究, 2010, 28(3): 83–89 REN X L, JIA Z K, DING R X, et al. Progress and prospect of research on root-zone water micro-collecting farming for crop in arid region of China[J]. Agricultural Research in the Arid Areas, 2010, 28(3): 83–89
[34] 宋秉海. 旱地地膜玉米“贫水富集”种植模式研究[J]. 中国生态农业学报, 2006, 14(3): 93–95 SONG B H. Study on planting models of rainwater harvesting technique of mulched maize in arid areas[J]. Chinese Journal of Eco-Agriculture, 2006, 14(3): 93–95
[35] 江燕, 刘昌明, 胡铁松, 等. 新安江模型参数优选的改进粒子群算法[J]. 水利学报, 2007, 38(10): 1200–1206JIANG Y, LIU C M, HU T S, et al. Improved particle swarm optimization for parameter calibration of Xin’anjiang model[J]. Journal of Hydraulic Engineering, 2007, 38(10): 1200–1206
[36] 俞欢军, 许宁, 张丽平, 等. 混合粒子群优化算法研究[J]. 信息与控制, 2005, 34(4): 500–504 YU H J, XU N, ZHANG L P, et al. Research on hybrid particle swarm optimization[J]. Information and Control, 2005, 34(4): 500–504
Sensitivity analysis and optimization of parameters for Laio soil moisture dynamic stochastic model for ridge-furrow rainwater harvesting system*
YIN Xinwei1,2, LI Xiaoling3, WANG Qi4**, ZHANG Yongmei1,2
(1. Fukang Station for Desert Ecosystem Observation and Experiment / Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. College of Water Conservancy and Hydropower Engineering, Gansu Agricultural University, Lanzhou 730070, China; 4. College of Grassland Science, Gansu Agricultural University, Lanzhou 730070, China)
Sensitivity analysis of parameters, calibration and validation of eco-hydrological modelsare essential for model evaluation and application. It is important in model application to accurately estimate the values of model parameters and to further improve model prediction capacity. Based on eco-hydrological process, the Laio soil moisture dynamics stochastic model (Laio model) was used to describe daily water balance in active soil depth of ridge-furrow rainwater harvest system during growing season to analyze the effects of the interactions among plants, soil and environment under different climatic conditions on soil water balance and plant water conditions. The performance of the Laio model varied with climatic zone due to the heterogeneity of climate, vegetation and soil characteristics. In this study, in order to establish an effective system for parameter sensitivity analysis, calibration and validation of the Laio model in a ridge-furrow rainwater harvesting system in a semi-arid area, a field experiment with a randomized complete block design was conducted during the 2012 and 2013 oat growing seasons at Dingxi Arid Meteorology and Ecological Environment Experimental Station. The experiment was designed to investigate the parameter sensitivity and to determine the optimal mode of parameter optimization of the Laio model under various mulching materials (common plastic film, biodegradable film mulch and manually compacted soil) and various ridge-furrow ratios (60 cm∶30 cm, 60 cm∶45 cm and 60 cm∶60 cm). The methods included multi-factor sensitivity analysis, simplex method (ISM), particle swarm optimization algorithm (PSO) and hybrid particle swarm optimization algorithm (HPSO). Also continuously monitored soil moisture, precipitation runoff and daily precipitation data for 2012–2013 were used to run the model. The results indicated that: (1) mean precipitation per rainfall event () and soil saturation degree at wilting point (w) were the most sensitive parameters for probabilistic density function of soil moisture [(s)] in different experimental treatments. While the sensitivity of(s) towas more obvious under low soil moisture content, that towwas more obvious under high soil moisture content. (2) There were good agreements among the results of modelling using optimized parameters of the Laio model for the three optimization algorithms (ISM, PSO and HPSO) and the observation values, which were determined from the(s) curve. This included curve peak value (CPV), curve peak position (PP), 95% confidence interval (CI95%) and consistency measure (CM). All of these indicated that the optimized parameters of the Laio model using the ISM, PSO and HPSO methods correctly estimated(s) of ridge-furrow rainwater harvesting. (3) The HPSO method not only improved global optimization performance, but also quickened convergence and gave robust results with good quality. It was an effective optimization method for the Laio model calibration and validation. The study improved the efficiency of model parameter calibration, upgraded the accuracy of model simulation results and provided guidance for application of the Laio model in ridge-furrow rainwater harvesting research.
Ridge-furrow rainwater harvesting system; Soil moisture dynamic; Laio soil moisture dynamic stochastic model; Sensitivity analysis; Model parameter optimization
, E-mail: wangqigsau@gmail.com
Aug. 14, 2017;
Nov. 28, 2017
10.13930/j.cnki.cjea.170737
S152.7
A
1671-3990(2018)05-0746-13
王琦, 主要从事牧草、草坪及作物节水灌溉方面研究。E-mail: wangqigsau@gmail.com 尹鑫卫, 主要研究方向为干旱区水文生态学。E-mail: xinweiyin@foxmail.com
2017-08-14
2017-11-28
* This study was supported by the National Natural Science Foundation of China (41461062, 41661059).
* 国家自然科学基金项目(41461062, 41661059)资助
尹鑫卫, 李晓玲, 王琦, 张永梅. 垄沟集雨系统Laio土壤水分动态随机模型参数敏感性分析及优化[J]. 中国生态农业学报, 2018, 26(5): 746-758
YIN X W, LI X L, WANG Q, ZHANG Y M. Sensitivity analysis and optimization of parameters for Laio soil moisture dynamic stochastic model for ridge-furrow rainwater harvesting system[J]. Chinese Journal of Eco-Agriculture, 2018, 26(5): 746-758
