空间计量中长度单位和距离测量

刘 民 杜晓爽 冯伟利

（1．北京东方计量测试研究所，精密电磁测量与校准实验室，北京 100086；2．北京无线电计量测试研究所，北京 100039；3．北京航天计量测试技术研究所，北京 100076）

1 空间维度与长度单位定义

我们在三维平直空间上建立的长度计量基准和距离测量方法如今遇到了新的挑战。传统计量理论与广义相对论相结合产生了空间计量理论，空间计量理论让我们站在四维时空中观察自然世界，重新考察曾经定义的物理量和基本单位［1,2］。于是发现二维球面上的所谓直线，对于三维空间的观者来说，其实是弯曲的测地线，三维空间的所谓绝对直线，对于四维时空的观者也是弯曲的测地线。1793年，法国科学院定义的长度单位是“以经过巴黎的地球子午线从北极到赤道距离一千万分之一为1米”［3,4］。地球子午线（经线）是二维曲面的测地线，站在地球表面上看子午线是直线，但在三维空间上看子午线是曲线。那么把二维空间所定义的直线尺度用于三维空间，必然存在曲线与直线之间固有的偏差。

假设，曲线的曲率半径为R，弧长为l，弦长为d，两者之间的偏差为：

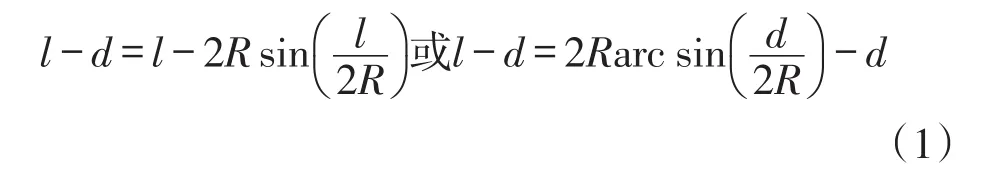
若地球半径R=6．4×106m，三维弦长直线距离d=（1～10）km，对应的二维弧长l以及相对偏差（l-d）/d，由式（1）计算可得数据，见表1。

表1 10km范围内二维线长与弧长的相对偏差Tab.1 The deviation between length of arc and chord in 2 dimension under range of 10km

可见在10km的距离上出现约1．017mm的偏差，造成这种偏差的原因是单位定义所选择的空间维度不同。同理，现在使用的长度国际单位SI米的定义是三维空间中测地线上的一段距离，在四维空间将会存在曲线与直线的微小偏差。

图1 用二维曲面的测地线定义单位长度Fig.1 The length unit defined by geodesic in 2-D

2 SI秒和SI米

1983年，第17届国际计量大会采用光速作为常数，重新定义长度单位：“米是光在真空中1/299792458s的时间间隔内的行程长度”［5］。这个定义说明了时间和空间是统一不可分割的。既然光速是常数，而时间测量受引力红移、相对速度效应等相对论效应的影响，那么空间中的距离也会在强引力场中变长，弱引力场中变短，相对速度大时变短，探索引力波的方法正是这个原理［6］。根据广义相对论，光线在引力场中会发生弯曲。而传统长度单位是基于欧几里得几何学，在平直的空间定义的，认为光是直线传播的。天文学用“光年”描述天体距离，观测恒星发光的强度和周期的变化来计算天体距离［7］。如果宇宙空间不是平直的，所观测的光线穿越各种引力场发生了弯曲，那么所计算的光年也就是测地线的弧长。并不是四维时空的直线距离。

国际单位制SI秒的定义是绝对定义的，不论在何种引力场下，不论相对运动速度如何，局域小空间内仍然要使用SI秒的定义复现时间单位，所测量的时间称为局域内的“原时”，即使受相对论效应的影响，不同局域上的原时各不相同，它们通过相对论公式可以换算成为“坐标时”，利用坐标时相互比较［8］。爱因斯坦的广义相对性原理要求“所有参考系中物理定律表达式相同”，进而要求长度单位定义也应是绝对定义的，每个局域空间内使用SI秒和光速常数c来复现长度单位SI米，使用原时测量光程间隔来测量空间距离。即使不同局域上的原时快慢不同，所测得的空间距离数值不同，通过相对论公式将原时换算为坐标时后，其测量结果就能相互比较了［9］。例如，在地面校准的1m标准尺子，送到空间站后，地面观者认为该尺子受到了相对论的尺缩效应将会变短。而空间站的宇航员使用SI秒和光速常数复现的长度基准进行测量，结果仍是1m，没有发生尺缩现象。这是因为空间站的SI秒受相对论效应影响，变快了。时间刻度和空间刻度同时成比例改变，在局域空间符合广义相对性原理。但是事实上，很多卫星，包括导航卫星在内，都对星载原子钟进行了修正，为保证与地面时间同步，卫星直接测量坐标时，不使用SI秒的测量原时。若空间站使用调整过的原子钟作标准，就会发现尺子缩短了。这就要求空间计量理论必须建立在广义相对论基础之上，用四维时空观理解空间距离测量问题。

3 惯性系与非惯性系

空间中的距离、速度、加速度等物理参数只有指定了参考系才有实际意义，测量他们之前必需定义好参考坐标系。爱因斯坦的狭义相对论仅适用于惯性系匀速运动的情况，不适用于有加速运动的非惯性系和有引力场存在的情况。光速各向同性以及光速不变原理也只适用于惯性系。惯性系的定义是“以绝对空间为参考，相对静止或保持匀速直线运动的参考系为惯性系”，该定义依赖绝对空间参考物。实际上不论地球、太阳、银河系中心还是河外星系都是运动变化的，不存在绝对参考物，所谓惯性系仅具有局域上的相对意义。给参考系定义了原点和坐标轴上的刻度后，就是坐标系。以银河系中心为参照物，可定义以太阳系质心为原点的局部惯性坐标系；以太阳为参照物，也可定义以地心为原点的局部惯性坐标系；惯性系的特点是坐标轴固定不能旋转。而坐标轴旋转的就是非惯性系，如地心地固坐标系以地球质心为原点，以地球自转轴为Z轴，以赤道面与零度子午线面交线为X轴，赤道面与90度子午面交线为Y轴，这样的非惯性坐标系跟随地球自转，周期为24h，这是我们熟悉的坐标系［10,11］。

4 转盘上测距问题

在惯性与非惯性坐标系上测量空间两点的距离，其影响量是不同的。例如在转盘上建立两种坐标系，如图2（a）所示。以盘心为原点，速度ω随盘旋转，非惯性坐标系表示为xμ=( )ct,r,θ,z；以盘心为原点，固定不转的惯性坐标系Xμ=( )cT,X,Y,Z。盘上有固定的A、B两点，用激光测量距离。B向A发射激光，经过时间Δt1到达A，A反射激光，经过时间Δt2到达B。因光速仅在惯性系中是常数，且直线传播，对于惯性系观者来说，因为A、B都在运动，当激光到达A时，A已运动到A'点，当反射光到达B点时，B已经运动到B''点，从图2（b）中可见，去程时间大于回程时间，Δt1＞Δt2。与惯性系不同的是，非惯性系的观者认为A、B相对静止，如图2（c）所示，光线弯曲，且去程和回程不经过同一条路径。转盘上的非惯性坐标系是典型的弯曲时空。而我们生活在类似转盘的地球上，习惯地使用了非惯性坐标系，为什么没有感到时空弯曲呢？为什么还固执地认为三点唯一确定一条直线是的真理呢？

图2 转盘上的惯性和非惯性坐标系Fig.2 The inertial and non-inertial coordination system on rotated plate

经计算地球赤道上相距10km的A、B两点，激光去程和回程相对偏差5．4E-8，约0．54mm。但是一去一回可相互抵消，双向测距的平均值与转盘静止状态时A、B距离相同。当前先进的仪器很难有这样的分辨力，能发现时空弯曲现象。

两坐标系的变换如式（2），假设没有引力作用，惯性系的时空可用闵氏空间表示，线元表达如式（3），对式（2）求导，代入式（3），得到转盘上的时空坐标线元表达如式（4）：

可见转盘上非惯性坐标系的坐标轴dt和dθ的度规和g22=r2均为变量，是弯曲的；坐标轴dr和dz的度规g11=1，g33=1，为常数，是平直的；dt和dθ轴之间的度规g02=g20=ωr2不为零，是相关，非正交的。转盘非惯性系上用激光测距，光子的运动方程为ds2=0，代入式（4）中，以dt为变量，求解一元二次方程（5），解得dt的表达式（6），其中正负号表示光程的两个方向［12］：

对式（6）的dt积分就是光子运行时间（坐标时）与空间坐标的关系，假设dz=0，因dr与光线弯曲的路径有关，留在积分号中，去程与回程弯曲的路径不同，Δt1与Δt2路径分别计算，在非惯性系的距离DAB计算非常复杂，如式（7）：

惯性坐标系的时空是平直的，用简单几何关系，很容易理解计算，如图2（b）。设三角形AOB的角度为φ，Δt1时间转动角度α，Δt2时间转动角度β。则去程距离DBA′和回程距离DA′B″的平均值为 AB 距离DAB：

式（9）和式（10）为隐函数，需要迭代求解。经计算，两个相对静止相距10km的点，按第一宇宙速度9．6km/s绕地球表面旋转（ω=1．5E-3rad/s），按上述激光去程和回程计算，相差11．24mm，但去程和回程的平均值表示两点距离，与ω=0情况偏差小于3．1nm，相对偏差为3．1E-13。

5 卫星与地面站的测距问题

卫星地面站与地球同步轨道的卫星之间进行测距时，也会受相对论效应影响，称为Sagnac效应［13,14］。以地心为原点建立两个坐标系，一个是跟随地球自转非惯性坐标系，另一个是固定不转的惯性坐标系，如图3所示。

在非惯性坐标系上的卫星A相对于地面站B静止，地面站B发送无线电测距信号给卫星A，卫星再返回该信号，地面B测量无线电信号往返时间，可计算星地距离。但在惯性坐标系的观者看来信号去程和回程不重合，且无线电信号传输路径大于两点直线距离。去程时间Δt1，回程时间Δt2，用非惯性系的距离计算式（7）计算A、B之间的测量值DAB，为简化计算，近似认为信号沿相同路径往返，则令dθ=0，再用一阶泰勒级数近似处理，DAB的表达式：

式（10）的最后一项就是弯曲时空造成的Sagnac效应。当转盘角速度ω=0时，时空是平直的，DAB=|rAB|，当角速度不为零时，弯曲时空造成了光线弯曲，出现Sagnac效应。

同样的情况，惯性系观者认为A和B都在运动之中，t1时刻B发送无线电信号，t2时刻A′反射，t3时刻B″再收到信号，这个过程中有如下关系：

假设惯性系中没有引力，不存在时空弯曲，空间对称的，则t2-t1=t3-t2=Δt≈|rAB|/c，且|rAB|=|rA′B′|，测量值为平均值：

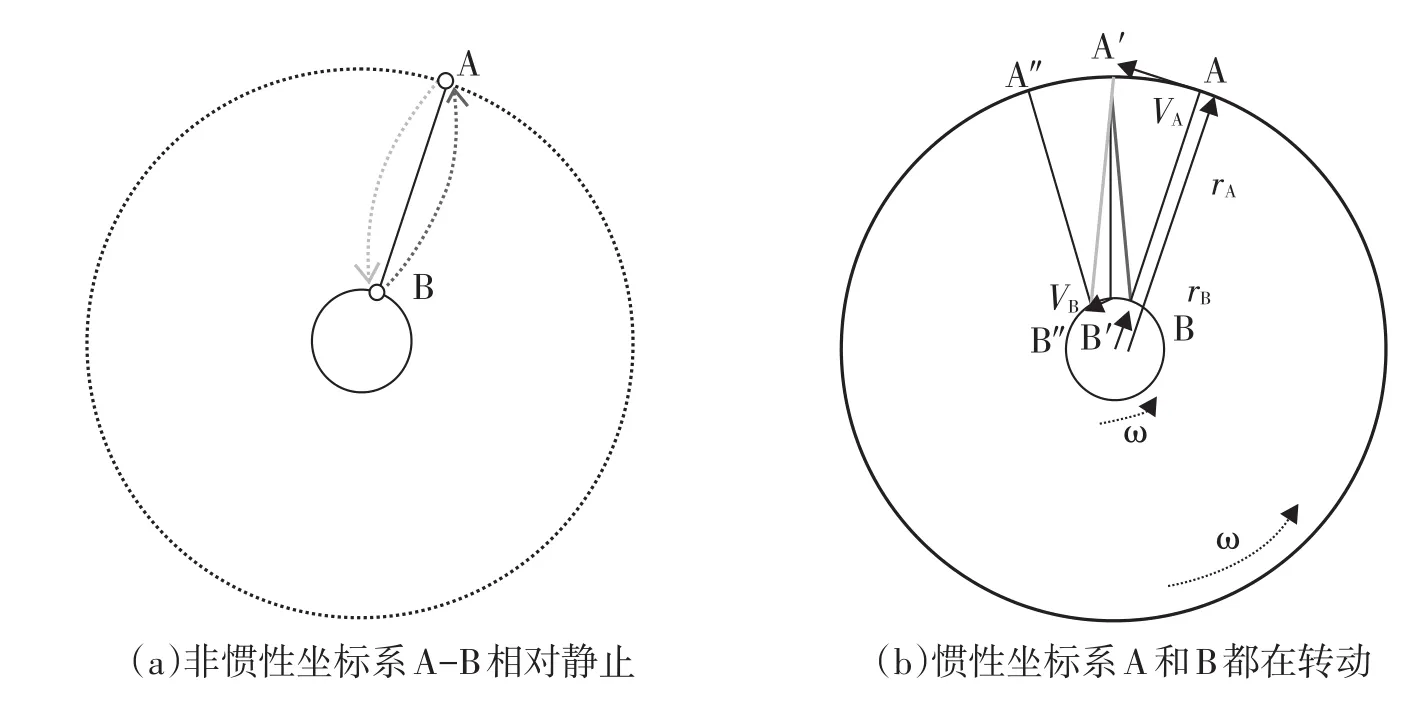
图3 卫星与地面站测距的Sagnac效应Fig.3 The sagnac effect of measuring distance between ground station and satellite

式（12）第一项与式（11）的第二项是相同的效应，对于非惯性系来说，因为相对静止，感觉到的就是时空弯曲造成的Sagnac效应，也是一种相对论效应。对于惯性系来说，因为信号传输时间和相对运动，造成了测量偏差，与非惯性系的Sangac效应等价。上述讨论是在没有引力场假设下得出的结论，仅为说明坐标系选择会影响测量结果，真实情况还要加入引力场造成的时空弯曲影响。广义相对论给出4维空间固有距离（或称为原距离）的公式［15］：

式中：gμυ——时空度规（metric）。

在广义相对论公式中μ,υ,i,j是区分坐标轴的符号，称为“指标”，表示第0,1,2,3坐标轴，不能当作指数运算符。第0表示时间轴，第1,2,3分别表示三维空间坐标轴。度规把坐标轴伸展成有刻度的坐标，度规给坐标轴刻度之间赋予一种比例关系，gμυ=0表示第μ和υ两坐标轴相互垂直，内积为零，或不相关；gμμ=常数（一般为1或c）表示第μ坐标方向平直；闵氏空间中的时间轴度规是c，表示时间均匀流失；gμμ=变量（或函数）表示第μ坐标方向弯曲；在狭义相对论的坐标系变换式中，时间轴度规为表示时间轴的刻度与相对速度u有关，在惯性系中u是常数，时间轴不弯曲，也是平直的。广义相对论中若g00是空间坐标的函数，表示时间轴弯曲，最简单的爱因斯坦方程近似解中，，表示时间刻度dt和径向刻度dr与引力势有关，质量球体周围的引力场中，时间和空间都是弯曲的。

6 结束语

空间计量理论将广义相对论与传统计量理论相结合，解决地球以外更广阔的宇宙空间的测量单位统一和测量准确问题，要求我们站在四维时空的角度理解物质的存在和运动规律。光的直线传播和光速不变原理仅适用于惯性坐标系和局域的平直空间。虽然我们已经习惯了随地球自传的非惯性坐标系，在其中没有感到弯曲空间和弯曲的光线，但是当我们的测量仪器准确度继续提高，当我们空间测量范围从局域推广到全域的话，诸如引力红移、相对速度效应、Sagnac效应等相对论效应将会成为测量不确定度的影响因素之一。

空间计量理论仍然认同SI秒和SI米的绝对定义，但要清晰地理解原时和坐标时的区别。在局域范围内使用SI定义复现的标准量值仅适用于局域范围，当该标准量值传递到其它局域空间时，必须用广义相对论公式换算为坐标时和坐标距离。

转盘上的非惯性坐标系有助于我们理解什么是弯曲的时空，光线为何不沿直线传播。在转盘上进行等半径测距和等角度测距时，均受到弯曲时空的影响。在不考虑引力的情况下，在惯性系中可以直接用几何公式解决测距问题，在非惯性系中必须使用广义相对论的时空度规解决测距问题。

［1］刘民．基本物理量定义在空间计量中的思考［C］．2015国防无线电&电学计量与测试学术交流会论文集，西安．

［2］Chunhao HAN,Zhiwu CAI．Concepts of Space-time and Measurement Units［C］．URSI-GASS2014,23th,Oct,2014,Beijing．

［3］Tenner Ed．The Trouble with the Meter［J］．Technology Review,2005,108（5）：73-73．

［4］朱星．采用自然衡量的新国际单位制［J］．物理，2014（7）．

［5］Barry N．Taylor,Ambler Thompson．The International Syetem of Units（SI）［M］．NIST Special Publication 330,2001 Edition,Natl．Inst．Stand．Technol．Spec．Pub．330,2008 Ed．,96 pages（March 2008）：18．

［6］王运永，朱兴江，刘见等．激光干涉仪引力波探测器［J］．天文学进展，2014，32（3）：348-383．

［7］晓泓．100亿光年从何而来［J］．科学（上海），2010（6）：95-96．

［8］马高峰，郑勇，杜兰等．时空参考系中的坐标和时间单位［J］．天文学进展，2010，28（4）：383-390．

［9］赵峥，刘文彪．广义相对论基础［M］．北京：清华大学出版社，2010．12：83．

［10］张科，薛舜，吕梅柏．地球范围内相对论效应下的时间转移与同步［J］．电子与信息学报，2014，36（8）：1992-1998．

［11］WANG Zhengbo,ZHAO Lu,WANG ShiGuang,et al．COMPASS time synchronization and dissemination-Toward centimetre position accuracy,Science China,Physics,Mechanics and Astronomy，2014，57，（9）：1788-1804．

［12］赵峥，刘文彪．广义相对论基础［M］．北京：清华大学出版社，2010．12：80．

［13］刘晓刚，张传定．星地双向时间比对Sagnac效应的计算和分析［J］．宇航计测技术，2009，29（1）：17-21．

［14］Neil Ashby．Relativity in the Future of Engineering［J］．IEEE Transactions on Instrumentation and Measurement，1994，43（4）：505-515．

［15］Matteo Luca Ruggiero,Angelo Tartaglia．A note on the Sagnac effect for matter beams［J］,European Physicals Journal Plus,2015,130：90．