带负项值的on-shelf效用项集并行挖掘算法
2018-05-09陈丽娟谢伙生
陈丽娟,谢伙生
(福州大学数学与计算机科学学院,福建 福州 350116)
0 引 言
近年来,高效用项集挖掘已成为数据挖掘领域的热门研究问题,高效用模式挖掘中每个事务中的项都有对应的内部效用值(如数量),每个项都有外部效用值作为兴趣度度量(如利润)。传统的高效用项集挖掘[1-4]是在外部效用值为正的情况进行挖掘的,但现实生活中存在外部效用值为负的场景,如商场推出的买赠活动,赠送的商品的利润值为负。针对此类问题,Chu等人提出了带负项值的高效用项集挖掘算法HUINIV[5],该算法框架为2阶段算法,候选项集的数量大,挖掘时间空间消耗大。Fournier-Viger等人提出了垂直类的带负项值的高效用项集挖掘算法FHN[6-7],该算法定义了考虑负项值的效用列表结构,相较于HUINIV算法,在时空效率上都有所提高。
在实际处理问题过程中,除了要考虑效用值外,往往与项的on-shelf时间段有关,例如:{外套,棉袜}这样的商品组合,在商场的数据库中可能不是高利润的,而在冬季可能是高利润的,一些商品在商场中由于季节等原因可能会频繁地上架下架,因而在挖掘过程中考虑on-shelf时间段,更具有现实意义。如果不考虑时间,这些组合可能会被忽略。针对该类问题,Lan等人提出了on-shelf效用项集挖掘算法TP-Hou[8],该算法在挖掘过程中不仅考虑了项的效用值,而且考虑了项的on-shelf时间段。Lan等人将效用值的取值范围扩展到负值,进一步提出了TS-Houn算法[9],该算法能够有效找到所有的带负项值的高on-shelf效用项集。但这类算法在挖掘过程中需要保存所有的候选项集以及多次数据库扫描,时间和空间的消耗都较大。Fournier-Viger等人进而提出FOSHU算法[10],该算法根据效用列表的特性进行剪枝,提高了挖掘效率,但最小on-shelf效用值过小时,算法需要构建大量的效用列表结构。
算法并行化是提高算法效率的一种有效途径[11-12],MapReduce是Google提出的一种编程框架,用于大规模数据的并行计算[13]。MapReduce框架通过对数据进行划分并提取出key/value键值对交给多个Mapper以及Reducer进行处理,从而达到并行化处理的目的,是目前较好的分布式数据处理框架[14-15]。本文将MapReduce平台引入带负项值的on-shelf效用项集挖掘中,将事务数据库根据时间段划分成小数据库,并行地在每个小数据库中进行高效用项集挖掘,提出带负项值的on-shelf效用项集并行挖掘算法DTP-Houn。实验结果表明DTP-Houn算法具有较好的挖掘效率。
1 相关定义与性质
假设I={i1,i2,…,im}是由m个不同项组成的项集合,项ik(1km)的外部效用值记为p(ik)。事务数据库D={T1,T2,…,Tn}是由n个事务组成的,D中的每个事务Tc(1cn)都是项集I的子集,唯一的标识符(Tid)为c。给定事务Tc,对于∀ik∈I其内部效用值记为q(ik,Tc)。记P={p1,p2,…,pn}是时间段的集合,对于每个事务Tc的时间段pt(Tc)都满足pt(Tc)∈P。数据库D如表1所示。每个项对应的外部效用值表以及时间段表如表2和表3所示。
表1 事务数据库D

Tid事务时间段1(a,1)(b,2)(c,3)12(a,2)(c,1)(d,2)(e,4)13(b,1)(d,2)(e,2)(f,3)(g,1)24(c,2)(d,1)(f,1)25(a,3),(b,3)(d,1)(g,2)3
表2 外部效用值表
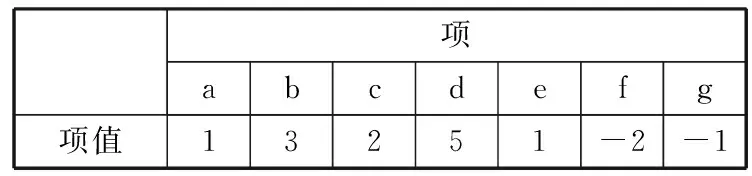
项abcdefg项值13251-2-1
表3 时间段表

项时间段123a101b111c110d111e110f010g011



定义4给定项集X,X的on-shelf效用值ou(X)=u(X)/to(X),记λ为自定义阈值(0λ1)即最小on-shelf效用值。若ou(X)≥λ,则项集X为高on-shelf效用项集。

定义6给定时间段h,项集X的on-shelf效用值ou(X,h)=u(X,h)/pto(h)。
带负项值的on-shelf效用项集挖掘的任务是找到所有的高on-shelf效用项集,其剪枝性质如下:
性质1给定项集X,若在任何一个时间段h都不满足ou(X,h)≥λ,那么项集X不可能为高on-shelf效用项集。
性质2给定项集X和时间段h,满足TWU(X,h)/pto(h)≥ou(X,h),这是由于TWU(X,h)≥u(X,h)总是成立的。
性质3给定项集X和时间段h,若X不满足TWU(X,h)/pto(h)≥λ,那么项集X不可能满足ou(X,h)≥λ,且X的扩展集X′也不可能满足ou(X′,h)≥λ。
2 DTP-Houn算法
现有算法[8-10]提出了不少策略来提升on-shelf效用项集挖掘效率,但计算成本仍然较大。TP-Hou算法是一种基于Two-phase[16]的算法,它也是最早将on-shelf时间段引入效用挖掘中的算法,但不能处理含负项值的情况。TP-Houn算法重定义了TP-Hou算法中的TWU计算方法(见定义5),由于TP-Houn算法为2阶段算法,所以算法需要多次I/O以及数据库扫描操作,面对数据量大的情况挖掘过程耗时较长。随着处理数据量的增加,其处理效率难以满足实际需求。为此,将MapReduce并行化框架也引入该问题的解决中来,充分利用其on-shelf时间段因素,将原始事务数据库按照时间段进行分片,将TP-Houn算法并行化,提出基于MapReduce的DTP-Houn算法,从而达到提高算法效率的目的。
DTP-Houn算法首先将原始事务数据库按时间段划分成n个分片数据库(n为时间段个数),并行地在每个时间数据库中挖掘高效用项集,算法需要一次MapReduce过程来完成项集挖掘。将原始事务数据库分片记为D={D1,D2,…,Dn},其中Dh(Dh∈D,1hn)是第h个时间段的分片数据库。在分片数据库Dh内,记长度为k的项集集合为Ck,如,1-项集集合为C1。记长度为k的候选项集集合为Lk,Lk为Ck的子集,计算方法为Lk={itemset|TWU(itemset,h)/pto(h)≥λ∧itemset∈Ck},为了便于算法描述,将其简记为Lk=Calculate(Ck)。对应地,Ck是由Lk-1中元素两两拼接得到的,简记为Ck=genCandidate(Lk-1)。长度为k的高效用项集集合为Hk,Hk是Lk的子集,其计算方法为Hk={itemset|u(itemset,h)/pto(h)≥λ∧itemset∈Lk} ,同样将其表示为Hk=genHighUtilityItem(Lk)。
在Map阶段(如算法1所示),算法首先扫描分片数据库计算1-项集的TWU,根据TWU的向下封闭性进行剪枝(性质3),生成1-候选项集。接着由1-候选项集拼接产生2-候选项集(行6-8),进而迭代产生k-候选项集,直至不再产生候选项集。最后,判断候选项集是否为高效用项集,并将生成的高效用项集作为key,<效用值,周期效用值,时间段>作为value输出到Reduce阶段。
算法1Map函数
输入:分片数据库Dh,最小on-shelf效用值λ
输出:
key为itemset,value为
1.扫描Dh,计算pto(h)以及Dh中每个项ik的u(ik,h)和TWU(ik,h);
2.L1=Calculate(C1);
3.H1=genHighUtilityItem(L1);
4.output
//输出到Reduce端
5.for(k=2;Lk-1≠Φ;k++)
6.Ck=genCandidate(Lk-1);
7.扫描Dh,计算Ck中每个itemset的u(itemset,h)与TWU(itemset,h);
8.Lk=Calculate(Ck);
9.Hk=genHighUtilityItem(Lk);
10.output
11.end for
Map阶段产生的高效用项集为高on-shelf候选项集(性质1),Reduce阶段需要计算候选项集的实际on-shelf效用值。在Reduce阶段(如算法2所示)由于itemset为key,所以相同的itemset会被分配到同一Reducer中。算法首先循环判断itemset的px(itemset)是否存在于Map阶段传递的value中,若存在则可以直接从value中获取,若不存在则需要扫描对应时间段的分片数据库计算得到。接着由定义4计算得到ou(itemset),若ou(itemset)≥λ,则itemset为高on-shelf效用项集,输出结果。
算法2Reduce函数
输入:最小on-shelf效用值λ,
key和value与Map函数输出一一对应
输出:
1.for时间段t in px(key)
2.if t∉value.h
//value中是否包含时间段t
3.扫描Dt,计算u(key,t)与pto(t);
4.end if
5.u(key)+=u(key,t);
6.to(key)+=pto(t);
7.end for
8.ou(key)=u(key)/to(key);
9.if ou(key)≥λ
10.output
11.end if
3 实验结果
为了验证DTP-Houn算法的有效性,将DTP-Houn算法和TP-Houn算法进行3类不同的实验比较。实验平台为由3台VM(1个Master,2个DataNode)构成的Hadoop集群,每台VM的配置为2个单处理器和2.5 GB内存,环境配置为Ubuntu 16.04.2和Hadoop 2.6.5。实验选取chess,mushroom, T10I4D100K,accidents这4个数据集[17],数据集的特征如表4所示。数据集中的内部效用值在区间[1,5]内随机产生,外部效用值是以对数正态分布在[-1000,1000]内产生的,时间段个数为5。
表4 数据集特征

数据集事务数项数目平均长度最长长度chess3196753636mushroom81241192323T10I4D100k10000087010.129accidents34018346833.851
3.1 最小on-shelf效用值影响实验
算法运行时间比较如图1所示。实验结果表明,在4个数据集chess,mushroom,T10I4D100K,accidents中,DTP-Houn算法的挖掘时间都少于TP-Houn算法,挖掘效率相较更高,这是因为DTP-Houn算法将大的数据库根据时间段划分为较小的数据库,充分利用集群的优势,将挖掘任务并行化运行在集群的DataNode上,使得算法运行效率提高。

(a) chess (b) mushroom

(c) T10I4D100K (d) accidents图1 运行时间比较
3.2 DataNode个数影响实验
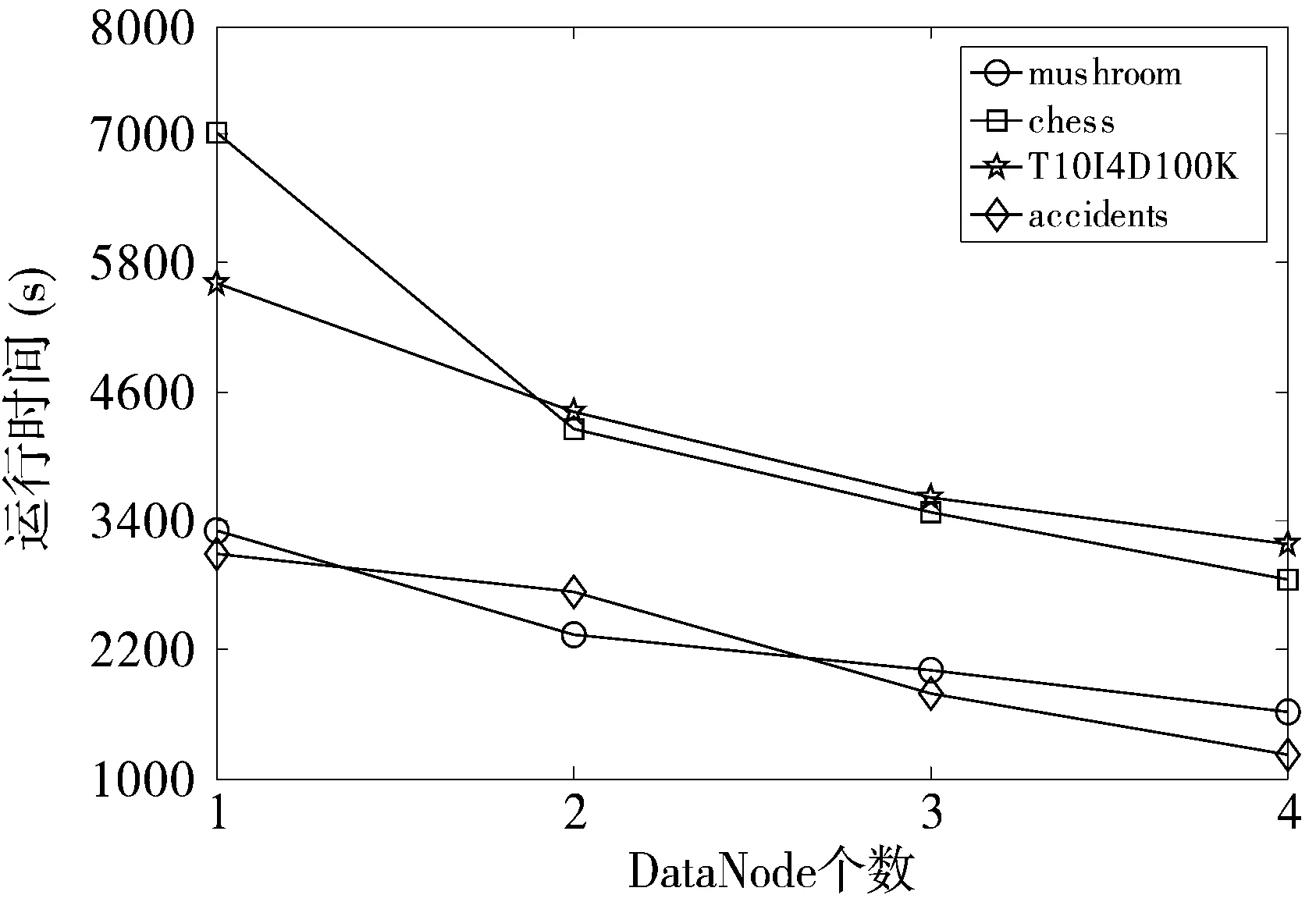
图2 不同DataNode个数下运行时间比较
在不同DataNode个数的集群下,DTP-Houn算法的运行时间比较如图2所示。DataNode配置均为2个单处理器和2.5 GB内存的VM。实验使用chess,mushroom,T10I4D100K,accidents这4个数据集,分别固定最小on-shelf效用值为0.86,0.26,0.4,0.43。从实验结果可以看出随着DataNode个数的增加,DTP-Houn算法的运行时间逐渐减少。这是因为DTP-Houn算法的挖掘任务能够并行运行在更多节点上,节省了每个节点的运行时间,但是节点的通信时间也会有所增加。然而,从实验结果可以看出,DTP-Houn算法的运行效率得到提高,能够较好地适应MapReduce平台。
3.3 on-shelf时间段个数影响实验
由于带负项值的on-shelf效用项集挖掘在挖掘中考虑了on-shelf时间段,相同最小on-shelf效用值的情况下,on-shelf时间段个数会影响高on-shelf效用项集数目。所以本文设计了不同on-shelf时间段个数对算法的影响实验,时间段个数分别为5,25,50,DataNode个数为2。实验选取数据量大的accidents数据集进行实验。不同on-shelf时间段个数下DTP_Houn算法和TP_Houn算法的运行时间比较如图3所示,从实验结果可以看出,不同的时间段个数下,DTP_Houn算法都比TP_Houn算法表现出较好的挖掘效率。
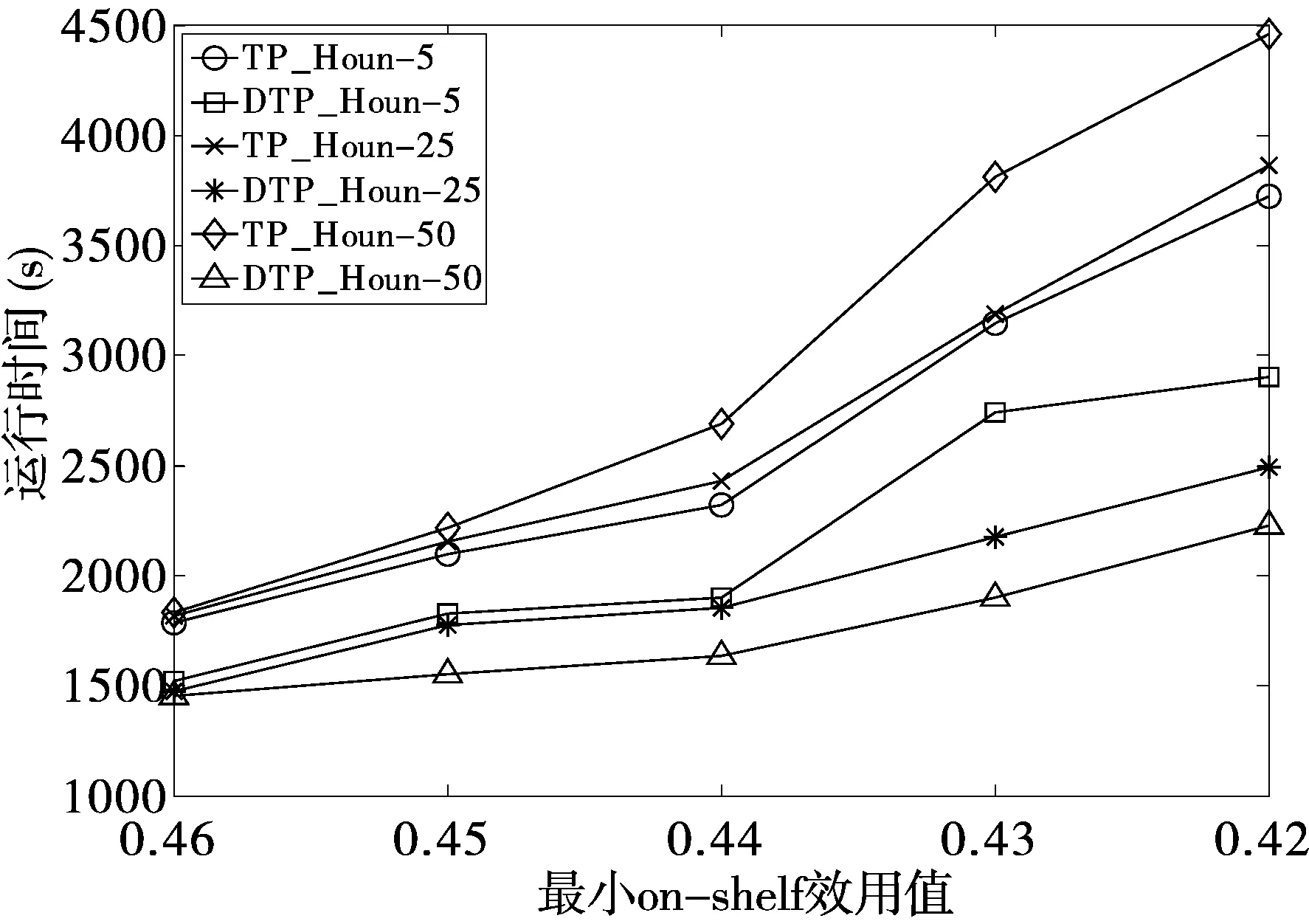
图3 不同on-shelf时间段个数下运行时间比较
4 结束语
本文研究了带负项值的on-shelf效用项集的并行化挖掘问题,提出了基于MapReduce的带负项值的on-shelf效用项集挖掘算法DTP-Houn。算法根据挖掘的时间段特性对原始数据库进行分片,使得挖掘任务能够并行化进行。实验从最小on-shelf效用值、DataNode个数和on-shelf时间段个数3个方面来验证算法的有效性,实验结果表明,DTP-Houn算法具有较好的挖掘效率。
参考文献:
[1] Liu Junqiang, Wang Ke, Fung B C M. Mining high utility patterns in one phase without generating candidates[J]. IEEE Transactions on Knowledge and Data Engineering, 2016,28(5):1245-1257.
[2] Jin Jue, Wang Shui. Rup/Frup-growth: An efficient algorithm for mining high utility itemsets[J]. Procedia Engineering, 2017,174:895-903.
[3] Krishnamoorthy S. Pruning strategies for mining high utility itemsets[J]. Expert Systems with Applications, 2015,42(5):2371-2381.
[4] Zida S, Fournier-Viger P, Lin Chun-wei, et al. EFIM: A fast and memory efficient algorithm for high-utility itemset mining[J]. Knowledge & Information Systems, 2017,51(2):595-625.
[5] Chu C J, Tseng V S, Liang T. An efficient algorithm for mining high utility itemsets with negative item values in large databases[J]. Applied Mathematics and Computation, 2009,215(2):767-778.
[6] Fournier-Viger P. FHN: Efficient mining of high-utility itemsets with negative unit profits[C]// Proceedings of the 10th International Conference on Advanced Data Mining and Applications. 2014:16-29.
[7] Lin Chun-wei, Fournier-Viger P, Gan Wensheng. FHN: An efficient algorithm for mining high-utility itemsets with negative unit profits[J]. Knowledge-Based Systems, 2016,111:283-298.
[8] Lan Guo-cheng, Hong T P, Tseng V S. Discovery of high utility itemsets from on-shelf time periods of products[J]. Expert Systems with Applications, 2011,38(5):5851-5857.
[9] Lan Guo-cheng, Hong T P, Huang J P, et al. On-shelf utility mining with negative item values[J]. Expert Systems with Applications, 2014,41(7):3450-3459.
[10] Fournier-Viger P, Zida S. FOSHU: Faster on-shelf high utility itemset mining with or without negative unit profit[C]// Proceedings of the 30th Annual ACM Symposium on Applied Computing. 2015:857-864.
[11] 李伟卫,赵航,张阳,等. 基于MapReduce的海量数据挖掘技术研究[J]. 计算机工程与应用, 2013,49(20):112-117.
[12] Al-Hamodi A A G, Lu Song-feng. MapReduce frequent itemsets for mining association rules[C]// Proceedings of the 2016 International Conference on Information System and Artificial Intelligence. 2016:281-284.
[13] 董新华,李瑞轩,周湾湾,等. Hadoop系统性能优化与功能增强综述[J]. 计算机研究与发展, 2013,50(S2):1-15.
[14] 杜江,张铮,张杰鑫,等. MapReduce并行编程模型研究综述[J]. 计算机科学, 2015,42(S1):537-541.
[15] 宋杰,孙宗哲,毛克明,等. MapReduce大数据处理平台与算法研究进展[J]. 软件学报, 2017,28(3):514-543.
[16] Liu Ying, Liao Wei-keng, Choudhary A N. A two-phase algorithm for fast discovery of high utility itemsets[C]// Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. 2005:689-695.
[17] Fournier-Viger P, Gomariz A, Lam H, et al. SPMF: Open-source Data Mining Platform[EB/OL]. http://www.philippe-fournier-viger.com/spmf, 2017-09-20.
