基于改进k-近邻的直推式支持向量机学习算法

李 煜，冯 翱，邹书蓉

(成都信息工程大学计算机学院，四川 成都 610225)

0 引 言

情感分析(Sentiment Analysis)指的是分析人们对诸如产品、服务、组织、事件、问题、主题等实体及其属性的观点、情感、评价、态度的研究领域[1]。随着互联网的普及，人们比过去更愿意和他人分享自己的生活、观点、经历和想法，这促使网络尤其是社交网络中涌现出大量主观文本数据，如何从大量文本数据中分析用户态度成为个人、商家和政府迫切需要解决的问题之一[2]。通常情况下，所能获得的文本数据往往是无标签的，若对其全部进行标注需要花费大量人力物力。因此，如何利用少量的标注数据对大量的无标签数据进行分类识别成为该领域主要难题之一。

统计学习理论是由Vapnik等人提出的针对小样本问题的机器学习理论[3-4]。支持向量机(Support Vector Machine, SVM)[5]是建立在统计学习理论基础上，以结构风险最小化为原则的一种学习算法。由于其良好的分类性能，该算法在图像和文本处理等众多领域得到了广泛的应用。

传统支持向量机根据学习样本进行训练得到分类超平面，并对测试样本进行预测。SVM具有良好的分类性能，但它要求每个学习样本标签已知。但在实际问题中，得到所有学习样本的标签需要花费较大代价。针对传统支持向量机的不足，Joachims等人提出直推式支持向量机模型(Transductive Support Vector Machine, TSVM)[6]。该模型可以利用少量有标签样本对无标签样本进行预测，可以在保证准确率的同时，较大幅度地减少对有标签样本的依赖。但当数据量较大时，TSVM模型构建需要花费大量时间。在保证算法准确率能满足实际应用要求的前提下，如何减少该算法的运行时间成为主要研究方向之一。

1 基本算法介绍

1.1 直推式支持向量机算法

文献[6-7]中提出一种直推式支持向量机学习算法，与传统SVM一样，TSVM也是针对二分类问题的学习方法。TSVM试图对未标记样本赋予不同的标签并找到在所有样本上间隔最大的分类超平面。下面对TSVM的基本原理进行简单介绍[8-9]。

(1)

(2)

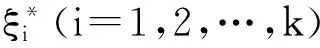
Step1用户指定影响因子C和C*，并使用传统支持向量机方法对有标签数据进行训练，得到一个初始分类器。

Step2用初始分类器对无标签数据进行分类，并按照分类结果给无标签数据赋予临时标签。

Step3使用支持向量机方法对全部样本进行训练，得到新的分类器。按照一定规则交换数据的临时标签，使得目标函数值最大程度地减小。

Step4逐渐增大C*，并返回Step3，直到C和C*相等为止。

Step1中用户指定C*应小于C，使算法执行初期有标记样本在算法中发挥更大作用。Step3中数据临时标签的交换是最小化目标函数的关键。Step4中C*的逐渐增大目的是增加无标记样本对算法的影响，使目标函数进一步最小化。

1.2 k-近邻算法

k-近邻算法(k-nearest neighbor, kNN)是一种常用的分类算法[10]，它是惰性学习[11]的显著代表，即没有明显的训练过程。训练阶段只将样本保存起来，当测试样本输入，算法开始执行。它的原理为找出每个样本最近的k个样本，k个样本中出现次数最多的类别即为该样本的类别，主要过程如下[12]：

1)给定训练样本集C={C1,C2,…,Cn}，样本类别集合w={w1,w2,…,wm}，设置k值。

2)对于样本Ci(i=1,2,…,n)，采取某种距离函数计算Ci与Cj(j=1,2,…,n,i≠j)的距离为dij，存入距离集合D。

D={dij|i=1,2,…,k; j=1,2,…,k; i≠j}

(3)

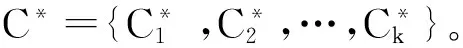
4)统计集合C*样本类别出现次数，出现次数最多的类别wi(i=1,2,…,m)即为测试样本的类别。

在k-近邻算法中，测试样本的k个近邻在一定程度上反映出测试样本的空间位置。若k个样本类别基本一致，则测试样本有很大概率属于该类别。若k个样本存在2个类别对应样本数目大致相同，则说明该样本位于这2个类的交界处。

1.3 k-均值聚类算法

k-均值聚类算法[13]是一种典型的无监督学习方法。它将数据集样本分为k个簇，使得簇内样本相似，簇间样本相异。聚类性能的衡量是由目标函数决定的，k-均值聚类算法的目标函数即最小化平方误差[14]：

(4)

其中μi是每个簇的均值向量，即每簇的中心，Ci是聚类完成后产生的簇划分，k为划分簇的个数，x为数据集中的样本。直观上看，该目标函数刻画簇内样本的紧密程度，即E值越小，簇内样本越紧密，相似度越高，算法主要过程如下[15]：

Step1输入样本集D={x1,x2,…,xm}，聚类簇数k和精度ε。

Step2从D中随机选择k个样本作为初始的中心点集μ={μ1,μ2,…,μk}。

Step3令Ci=Φ(1ik)，遍历数据集，计算样本xj和各中心点μi(1ik)的距离。

dji=‖xj-μi‖

(5)

Step4确定xj的簇标记，将样本xj加入对应的簇Cλj=Cλj∪{xj}。

λj=arg mini∈{1,2,…,k}dji

(6)

Step5重新计算k个中心点。

(7)

Step6计算目标函数E，若满足式(8)，算法结束，否则，返回Step3。

|En-En-1|<ε

(8)

事实上，最小化式(4)需要考察样本集D所有可能的簇划分，这是一个NP问题。k-均值聚类算法采用了贪心算法的思想，通过迭代优化找出近似解，但初始中心点和k值的选取会影响算法的执行结果。

2 算法设计

2.1 原理分析

TSVM成功将直推式学习思想引入算法中，利用无标签数据和少量的有标签数据构建分类器。相对于传统的支持向量机，该算法结合无标签数据隐藏的分布信息，在分类性能上有一定提高。但是，TSVM求解过程需要遍历所有无标签样本，当数据量较大时，算法执行时间较长。文献[16-17]中提出了2种解决方式，但都存在一定缺陷。为了在保证准确率的前提下进一步提高TSVM模型的运行速度，本文提出一种基于改进k-近邻的直推式支持向量机学习算法(k2TSVM)。

该算法思想如下：若仅使用k-均值算法将无标签样本分为k簇，每簇样本赋予相同标签，然后对无标签样本集所有2k种分类结果进行训练和学习，选择分类效果最好的作为最终分类器，算法虽然在一定程度上对数据集进行压缩，但是学习所有分类可能仍需花费较长时间。由支持向量机可知，算法目标是最大化支持向量到分类超平面的几何间隔，支持向量机分类超平面仅仅取决于少数支持向量，即位于2类交界处的样本对分类器起决定作用。利用这点删除远离分类面样本，在一定程度上可以加快算法执行速度，但依然需要遍历无标签样本。由聚类算法特性可知，簇内样本相似，簇间样本相异，因此一种新思路是在进行k-近邻算法前先对无标签样本进行k-均值聚类，分为若干簇。由于簇内样本相似，使用每簇中心点作为簇的代表进行k-近邻算法，若该中心点的k个近邻类别大致相同，则认为该类样本远离2类交界面，可将该簇样本删除。这种方法可以减少k-近邻算法的测试样本数，进一步提高算法的执行速度。

2.2 算法主要步骤

k2TSVM算法解决二分类问题的主要步骤如下：

Step1输入有标签样本集合Dl={Dl1,Dl2,…,Dlm}和无标签样本集合Du={Du1,Du2,…,Dun}。

Step2根据无标签样本总数n的大小估计簇数k1，使用k-均值算法将无标记数据进行聚类，将其分为k1簇，记录其均值向量集合μ={μ1,μ2,…,μk1}。

Step3根据有标签样本总数m的大小估计近邻数k2，设置阈值θ,i=1。

Step4采用某种距离函数计算中心点μi和有标签样本Dlj(1jm)的距离，此处选取余弦相似度，则中心点μi和有标签样本Dlj的相似度可定义为：

(9)

Step5统计中心点μi的k2个近邻样本属于正类个数为numpos，属于负类个数为numneg，若满足式(10)，则表明该均值向量所属簇远离2类交界处，将该簇无标记样本从Du中删除。

(10)

Step6i=i+1；如果ik1，返回Step4。

Step7将有标签数据集合Dl和剩余无标签数据集合Du作为训练集输入TSVM算法中进行分类器构建。

3 实验结果

根据上面提出的算法，采用SVM-Light工具箱的路透社文章数据集和SVMlin工具箱的路透社文章数据集对算法进行实验，该算法在SVMlin代码基础上使用C++语言实现。实验软件环境：Ubuntu-16.04，硬件环境：Intel i5-4590s处理器，3.00 GHz主频，8 GB内存的PC机。2个数据集具体情况如表1所示。

表1 2个数据集情况介绍

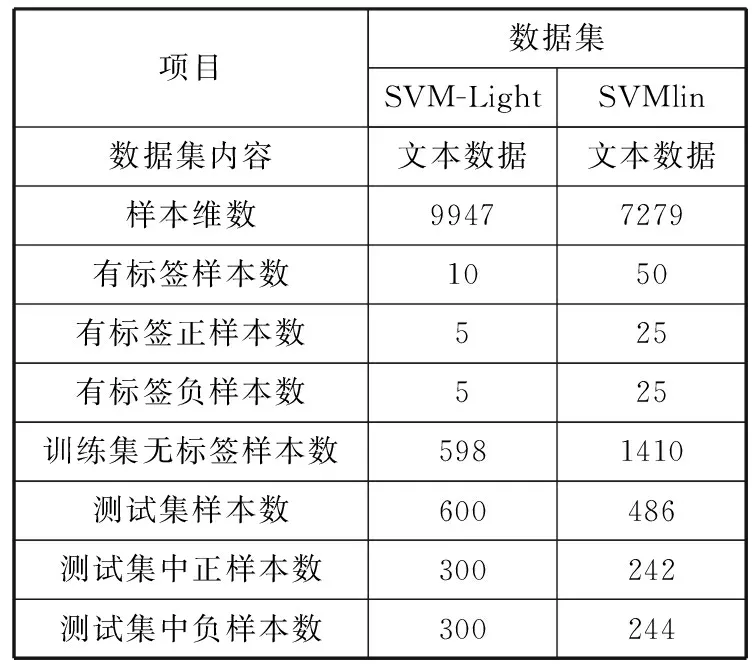
项目数据集SVM-LightSVMlin数据集内容文本数据文本数据样本维数99477279有标签样本数1050有标签正样本数525有标签负样本数525训练集无标签样本数5981410测试集样本数600486测试集中正样本数300242测试集中负样本数300244

为了验证k2TSVM算法的有效性，采用文献[11]中的k-近邻法作为实验的对照算法，记为knn-TSVM。使用上述2个数据集，对原始TSVM, knn-TSVM和k2TSVM算法进行分类实验比较，结果分别如表2和表3所示。

表2 3种算法使用第1个数据集的实验结果对比

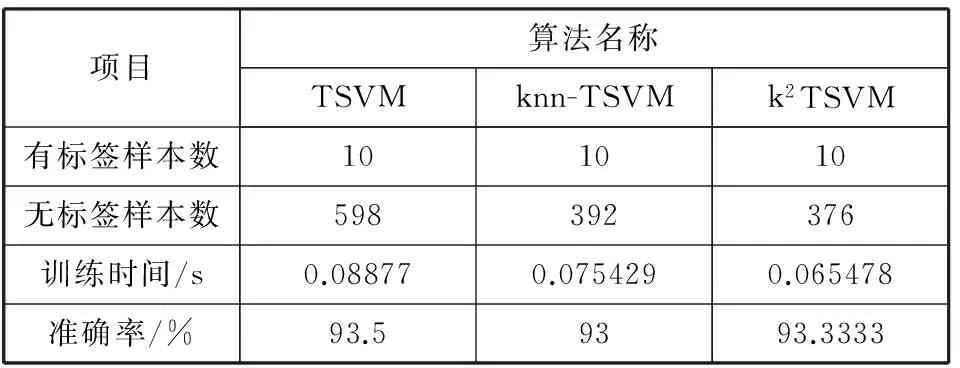
项目算法名称TSVMknn-TSVMk2TSVM有标签样本数101010无标签样本数598392376训练时间/s0.088770.0754290.065478准确率/%93.59393.3333

从表2实验结果可得：1)knn-TSVM算法和k2TSVM算法对数据集均有一定删减，样本数分别减少34.4%和37.1%。2)2种改进算法训练时间与原始算法相比都有下降，分别下降15%和26%。3)在准确率方面，由于数据量的减少，2种改进算法准确率分别下降0.5%和0.167%，虽然准确率均略微下降但能够满足实际应用要求。由实验结果可知，k2TSVM算法在减少样本数量，降低训练时间的幅度和准确率3个方面表现均优于knn-TSVM算法。

表3 3种算法使用第2个数据集的实验结果对比

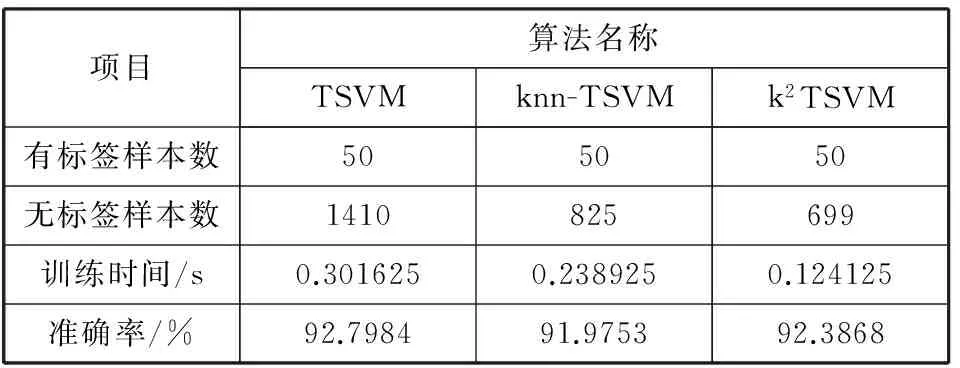
项目算法名称TSVMknn-TSVMk2TSVM有标签样本数505050无标签样本数1410825699训练时间/s0.3016250.2389250.124125准确率/%92.798491.975392.3868

从表3实验结果可得：1)knn-TSVM算法和k2TSVM算法样本数分别减少41.5%和50.4%。2)2种改进算法训练时间与原始算法相比都有下降，分别下降20.8%和58.9%。3)在准确率方面，2种改进算法准确率分别下降0.82%和0.41%。由实验结果可知，随着数据集样本数量的增加，k2TSVM算法在减少样本数量，降低训练时间的幅度2个方面表现均优于knn-TSVM算法且领先幅度比表2明显。在准确率方面，k2TSVM算法准确率稍优于knn-TSVM算法，虽与原算法相比略有下降，但能够满足实际应用需求。

4 结束语

本文提出了一种基于改进k-近邻的直推式支持向量机学习算法——k2TSVM，该算法在保证算法准确率能满足实际应用需求的前提下有效降低了TSVM模型计算复杂度。实验结果表明，该算法在运行时间和准确率方面均优于基于k-近邻的直推式支持向量机学习算法。

该算法的不足之处是算法性能很大程度上取决于k-均值聚类算法执行结果，但k-均值聚类对于离群点和孤立点敏感。一种改进的方法是在进行k-均值聚类前先将离群点删除，减少离群点对算法的影响。

参考文献：

[1] Liu Bing. Sentiment Analysis and Opinion Mining[M]. Morgan & Claypool Publishers, 2012.

[2] 谢丽星,周明,孙茂松. 基于层次结构的多策略中文微博情感分析和特征抽取[J]. 中文信息学报, 2012,26(1):73-83.

[3] Vapnik V. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 1995.

[4] Vapnik V. Statistical Learning Theory[M]. New York: John Wiley and Sons, 1998.

[5] Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995,20(3):273-297.

[6] Joachims T. Transductive inference for text classification using support vector machines[C]// Proceedings of the 16th International Conference on Machine Learning. 1999:200-209.

[7] Joachims T. Transductive support vector machines[M]// Semi-Supervised Learning. MIT Press, 2006:105-118.

[8] Joachims T. Learning to Classify Text Using Support Vector Machines: Methods, Theory and Algorithms[M]. Kluwer Academic Publishers, 2002.

[9] 陈毅松,汪国平,董士海. 基于支持向量机的渐进直推式分类学习算法[J]. 软件学报, 2003,14(3):451-460.

[10] Cover T M, Hart P E. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967,13(1):21-27.

[11] Aha D W. Lazy learning[J]. Artificial Intelligence Reviews, 1997,11(1-5):7-10.

[12] Keller J M, Gray M R, Givens J A. A fuzzy k-nearest neighbor algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985,15(4):580-585.

[13] Kanungo T, Mount D M, Netanyahu N S, et al. An efficient k-means clustering algorithm: Analysis and implementation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002,24(7):881-892.

[14] 周志华. 机器学习[M]. 北京:清华大学出版社, 2016.

[15] Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2003,36(2):451-461.

[16] 王立梅,李金凤,岳琪. 基于k-均值聚类的直推式支持向量机学习算法[J]. 计算机工程与应用, 2013,49(14):144-146.

[17] 廖东平,王书宏,黎湘. 一种结合k-近邻法的改进的渐进直推式支持向量机学习算法[J]. 电光与控制, 2010,17(10):6-9.