基于改进k-means算法的文本聚类

蒋 丽，薛善良

(南京航空航天大学计算机科学与技术学院，江苏 南京 211106)

0 引 言

互联网的快速发展带动着电子商务的发展，电子商务会产生大量的数据，合理分析这些数据，从中挖掘出客户感兴趣的信息，将会给企业带来巨大的利润。在电子商务平台上进行数据挖掘已经成为研究的热点问题，而电子商务网站中存储的大多是非结构化数据，比如文本[1]，因此，文本挖掘是面向电子商务进行数据挖掘重要的研究角度之一。

首先，与传统的数据挖掘相比，文本挖掘最大的特点是文本是非结构化的数据，为了把数据挖掘的算法应用在文本对象上，必须对文本进行处理，使文本最终表示为一种结构化形式[2]。传统的文本表示模型是以统计词频得出特征的权重形成向量，但这种方法忽略了词和词之间的语义性从而降低了聚类精度。其次，原始k-means算法在簇密集且簇与簇之间区别明显的数据中聚类效果较好，对文本聚类具有一定的局限性[3]。

1 k-means算法及Word2vec

1.1 k-means算法思想

1967年，MacQueen提出了k-means算法，它是一种基于划分的经典聚类算法[4]。该算法随机选择k个数据样本作为初始聚类中心，在每次迭代过程中，根据计算相似度将每个数据样本分配到最近的簇中，然后，重新计算簇的中心，也就是每个簇中所有数据的平均值。该算法结束的条件为聚类准则函数达到最优即收敛，从而使生成的每个聚类内紧凑，类间独立[5]。

1.2 k-means聚类算法步骤

Input：包含n个数据对象的数据集合D以及聚类数k。

Output：满足聚类准则函数收敛的k个聚类簇。

Step1从数据集合D中随机选择k个数据对象作为初始聚类中心cj,j=1,2,…,k。

Step2求出每个数据对象与聚类中心的距离d(xi,cj),i=1,2,…,n;j=1,2,…,k。

Step3根据求出的距离，将每个数据对象划分到最相似的簇中，即若满足d(xi,cj)=min{d(xi,cj′),j′=1,2,…,k}，则xi∈Yj,Yj表示聚类中心为cj的簇。

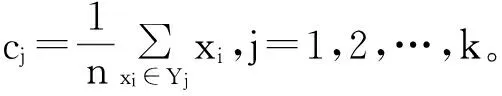
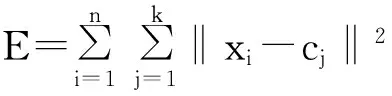
1.3 Word2vec分析

传统的具有代表性的文本表示方法有向量空间模型(Vector Space Model, VSM)[6]、布尔模型(Boolean Model, BM)[7]以及概率模型(Probabilistic Model, PM)[8]等。这些模型从不同的角度出发，使用不同的方法处理特征加权、类别学习和相似计算等问题。但是，它们各具缺点，比如基于VSM的聚类方法是按词频统计信息，得出特征的权重形成向量，而忽略了词和词之间，以及文档和文档之间的语义相关性，从而导致聚类的质量不高。基于此，本文采用Word2vec[9],Word2vec是Google在2013年开源的一款将词表征为词向量[10]的高效工具[11]，Word2vec可以考虑上下文的语义，能在一定程度上提高聚类的准确性。

当人们在说Word2vec算法或模型的时候，其实指的是其背后用于计算的2种语言模型，分别为CBOW和Skip-gram模型(如图1所示)。从图1可以看出，2个模型都包含输入层、投影层以及输出层。CBOW模型是在已知当前词wt的上下文wt-2,wt-1,wt+1,wt+2的前提下预测当前词wt；而Skip-gram模型是在已知当前词wt的前提下，预测其上下文wt-2,wt-1,wt+1,wt+2[12]。

(a) CBOW模型

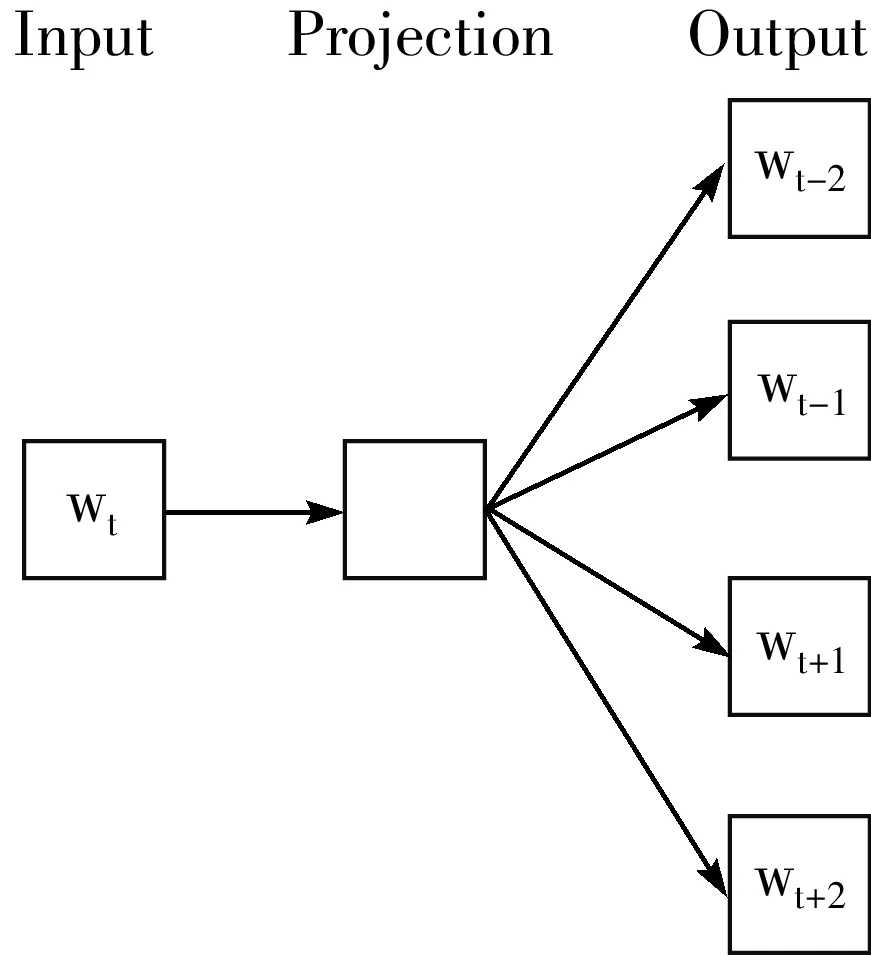
(b) Skip-gram模型

对于CBOW和Skip-gram模型，Word2vec给出了2套框架，它们分别基于Hierarchical Softmax和Negative Sampling来进行设计(如表1所示)[13]。

表1 Word2vec词向量训练框架

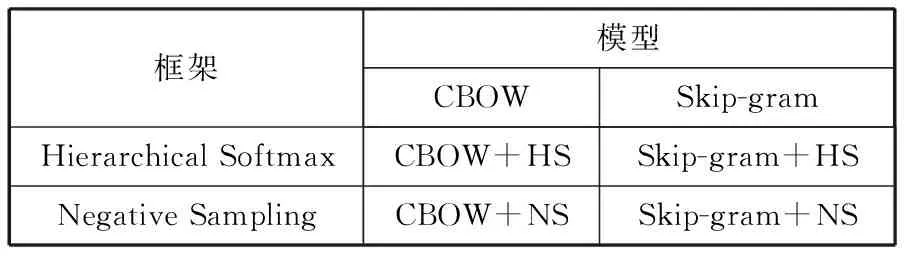
框架模型CBOWSkip-gramHierarchicalSoftmaxCBOW+HSSkip-gram+HSNegativeSamplingCBOW+NSSkip-gram+NS

1.4 Word2vec训练词向量的原理(CBOW+HS)

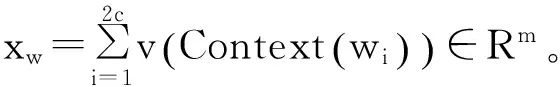
在模型的训练过程中，梯度是训练参数更新的依据[12]。为了获得梯度公式，需要构造训练模型的目标函数，该训练框架优化的目标函数通常取为如下对数似然函数：

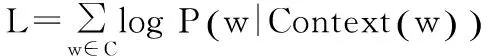
(1)

其中，C表示语料，Context(w)表示词w的上下文，即w周边的词的集合。条件概率P(w|Context(w))的公式可写为：

(2)

其中：

(3)

将式(2)代入式(1)中得到CBOW模型的目标函数即：

(4)

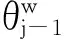
(5)

最后将求出的词向量用于聚类算法中。

Word2vec训练出来的词向量形式如图2所示。

图2 Word2vec训练出来的词向量形式

词向量的维度常常介于50～200维，维度越高词的特征表现越丰富，但训练时间和使用时的计算时间也会相应增加，本文使用较为常用的100维来进行Word2vec的训练。

2 改进后的k-means算法思想

原始的k-means算法对聚类数k的选取十分敏感，不同的初始值可能会导致不同的聚类结果。聚类的结果对聚类数k的依赖性导致聚类结果不稳定，且原始的k-means算法适用于簇密集但簇与簇之间区别较明显的数据，但在文本聚类上具有一定的局限性。文本之间的区别没有数据之间那么明显，文本之间存在很多近似词。原始的k-means算法随机输入聚类数k，如果文本的类别不符合聚类数k的值，不同类别的文本将被强行聚类到同一个类簇中。假设文本有7个类别，原始k-means算法将k设置为4，那么有3类将被强行划分到这4个类别中。这样的聚类结果是不太合理的。基于此，本文提出一种改进的k-means算法，该算法首先根据相似性将数据划分为k+x个簇，其中x为未知数，对于某个未知新样本，如果与现有的k(假设k=4)个初始聚类中心足够相似，那么就放入k个聚类中心中的某一个类中，否则就新增加一类(这时k+1=5)。将所有数据划分为k+x类后再根据类与用户的相似性使用k-means算法，改进后的k-means算法减少了结果对参数的依赖且聚类结果更准确。

2.1 基于共现词的相似度

从直观上来说，2个句子出现的共同词汇越多说明其相似度越大[16]。相似度不仅受到共同词汇的影响，同时还要结合句子的总数来进行度量，可以用如下公式直观地表达该思想：

(6)

其中，cos (A,B)>0.03表示输入句子A和B之间共现的词汇数目，考虑到词汇“连衣裙”和“裙子”虽不是共现词，但它们属于相似物品，故采用该公式。A和B代表搜索记录，利用第1章中训练出来的词向量直接进行计算。

(7)

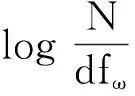
2.2 改进后的k-means算法步骤

Input：包含n个数据对象的数据集合D，k个初始聚类中心。

Output：满足聚类准则函数收敛的k+x个聚类簇。

Step1取一部分数据，让它们互相作相似性比较，得出相似度的阈值判定。

Step2从数据集合D中随机选择k个数据对象作为初始聚类中心并保证k个数据对象不重复(通过比较它们之间相似性，如果高于相似阈值则重新选择)。

Step3求出每个数据对象与聚类中心的相似度并将数据集合划为k+x类(通过基于共现词的相似度计算，2个记录的相似度大于等于相似阈值，则认为这2个记录为一类，如果小于相似阈值，则新增一类，从而更新聚类中心)。计算出的用户和类簇的相似度可以用矩阵来表示，矩阵的行代表类簇的个数，矩阵的列代表用户的个数。

Step4重新计算簇的聚类中心，取k+x个簇中相似度的中心值。

Step5计算相似度矩阵中数据与聚类中心的距离，将每个数据聚类到离该点最近的聚类中。

Step6反复执行Step4和Step5，直到聚类中心点不再发生变化。

2.3 改进后的算法流程图

改进后的算法流程如图3所示。

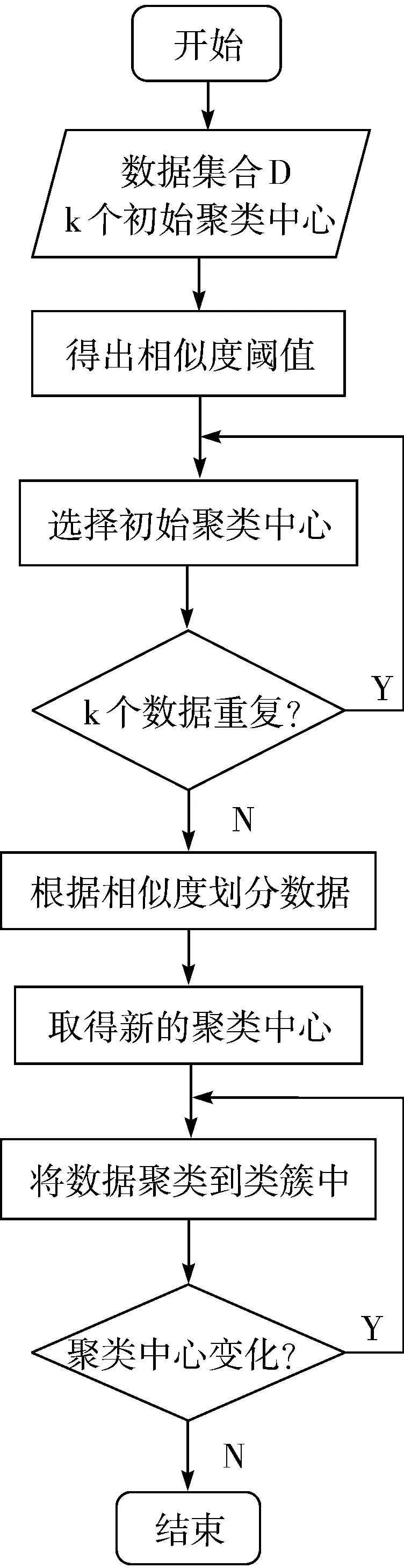
图3 改进后的k-means流程图

3 仿真实验分析

为了检验改进算法的有效性，对原始算法和改进算法进行对比实验，用于实验的CPU是Intel(R) Core(TM) i5-3210M CPU@2.50 GHz，内存为4 GB，实验软件环境：操作系统为64位Win7，编程软件用Eclipse。实验所采用的数据是从ofbiz网站上获取的用户的点击记录，该记录是通过用户在电商网站中点击商品时，调用商品详情接口里添加的存放用户浏览记录的代码，将用户的浏览记录存入一个对应的文本文档中就得到了如图4所示的部分用户浏览记录(因为浏览记录过多，所以只截取了前面30位用户的浏览记录)。为了缩短用户id的显示，将用户名改为用户a1、用户a2等(聚类结果的好坏以及正确与否都将有评判标准，在数据量少的情况下，聚类结果的正确以及好坏是可以通过观察得知，如多次聚类效果理想，则可以用于多用户的浏览记录中)。采用“结巴”分词工具对记录进行分词，将分词的结果用Word2vec训练出词向量，再利用原始的k-means算法和改进后的k-means算法分别做实验进行对比观察结果。实验的数据被分为7类，原始的k-means算法输入聚类数k=4，很多数据被聚类到不正确的类簇中，但改进后的k-means算法会根据相似度自动将类簇划分为k+x个簇(k=4，x=3)，减少了聚类数k的误差。

图4 部分用户浏览数据

原始k-means算法聚类结果如图5所示，改进后的k-mean算法聚类结果如图6所示。

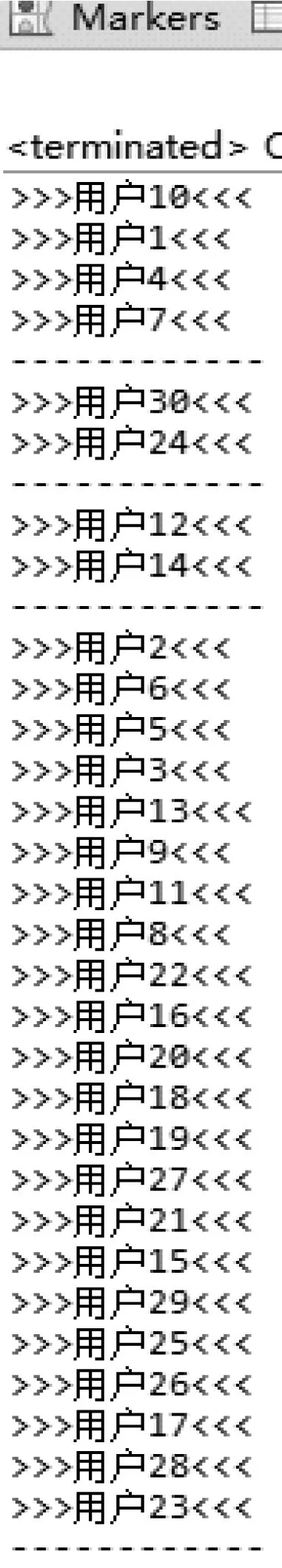
图5 原始k-means算法聚类结果

图6 改进后的k-means算法聚类结果

数据集相同的情况下，原始k-means聚类算法针对文本聚类准确率只有70%，聚类质量不优，聚类结果没有多大的参考意义，改进后的k-means聚类算法准确率达到97%，聚类结果更具有参考价值。如表2所示。

表2 原始k-means与改进的k-means聚类算法的准确率对比/%

原始k-means算法改进的k-means算法7097

4 结束语

k-means聚类算法是一种被广泛应用的算法，但k-means聚类算法对有些特殊的数据无法进行较精确的聚类。因此，需要根据特定的情况改进k-means算法中的某些地方。实验结果显示，本文提出的算法确实是有效的，当然在实验过程中也发现存在的一些不足，比如实验所需的时间复杂度比较高。下一步将考虑如何降低改进k-means算法的时间复杂度。

参考文献：

[1] 张宏兵. Web文本挖掘技术在网页推荐中的应用研究[D]. 南京:南京理工大学, 2013.

[2] 于宽. 改进K-means算法在文本聚类中的应用[D]. 大连:大连交通大学, 2007.

[3] 邓海. 降维多核K-Means算法在文本聚类中的研究[D]. 南宁:广西大学, 2013.

[4] 程杨. 中文短文本聚类算法的研究[D]. 长春:吉林大学, 2016.

[5] 杨河彬. 基于词向量的搜索词分类、聚类研究[D]. 上海:华东师范大学, 2015.

[6] Wu Xindong, Kumar V, Quinlan J R, et al. Top 10 algorithms in data mining[J]. Knowledge and Information Systems, 2008,14(1):1-37.

[7] 朱明. 数据挖掘[M]. 合肥:中国科学技术大学出版社, 2002.

[8] Salton G. Automatic Text Processing: The Transformation, Analysis, and Retrieval of Information by Computer[M]. Addison-Wesley, 1989.

[9] Baeza-Yates R, Ribeiro-Neto B. Modern Information Retrieval[M]. Addison-Wesley, 1999.

[10] Mikolov T. Word2vec Project[EB/OL]. https://code.google.com/p/word2vec/, 2014-09-18.

[11] Turian J, Ratinov L, Bengio Y. Word representations: A simple and general method for semi-supervised learning[C]// Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics. 2010:384-394.

[12] 周练. Word2vec的工作原理及应用探究[J]. 科技情报开发与经济, 2015,25(2):145-148.

[13] 熊富林,邓怡豪,唐晓晟. Word2vec的核心架构及其应用[J]. 南京师范大学学报(工程技术版), 2015,15(1):43-48.

[14] 唐明,朱磊,邹显春. 基于Word2vec的一种文档向量表示[J]. 计算机科学, 2016,43(6):214-217.

[15] 董文. 基于LDA和Word2vec的推荐算法研究[D]. 北京:北京邮电大学, 2015.

[16] 刘敏. 基于词向量的句子相似度计算及其在基于实例的机器翻译中的应用[D]. 北京:北京理工大学, 2015.