基于粒度决策熵的属性约简

李 华，江 峰，于 旭，杜军威，刘国柱

(青岛科技大学信息科学与技术学院，山东 青岛 266061)

0 引 言

在1982年的时候，波兰有名的数学家Pawlak就提出了著名的粗糙集理论[1]。具体来说，粗糙集理论是一种数学工具，它主要是用来描绘数据的不完整性和不确定性。人们用该理论来刻画数据的不精确性，并且可以从数据中得出隐含的大量知识，还可以得出数据之间的规律性。粗糙集的主要研究之一可以说是属性的约简[2]。一个好的约简算法不仅可以除去数据集中不相关的属性还能确保整体系统的分类能力和决策能力，从而简化知识表示，并提高系统处理的效率，方便用户的决策。

现在国内许多学者致力于研究属性约简的方法，并且已经提出了许多求解的算法，例如基于正区域的属性约简算法[3-5]、基于信息熵的属性约简算法[6-8]和基于差别矩阵的属性约简算法[9-10]等。在进行数据集的约简时，可能会得到多个约简集，然而人们希望能够找出最小的即最优的那个约简集。现有的约简算法已经表明了找寻最优的约简集是一个NP-hard的问题。所以，已经提出的约简算法把找寻最优约简的目标改为了找寻尽可能小的约简，同时还能够降低计算的时间复杂度和空间复杂度即计算的开销。在进行属性约简时，需要对数据集中属性的重要度进行概括总结，并且同时给出定义。而当前来看，人们定义属性重要度主要是基于代数和信息论2种观点。具体来讲，人们用代数观点定义属性重要性主要是考虑代数学中的集合运算和不可分辨关系，而用信息论观点来定义时主要是考虑信息论中信息熵的作用[11]。

在1948年的时候，香农提出了一种新的理论概念即信息熵理论，人们把香农提出的信息熵理论概念应用到处理信息的量化度量方面，来解决在数据集的约简中数据的量化度量难题。这些年来，随着人们把信息熵引入粗糙集理论中，很多新的有效的理论概念被提出来。例如，学者们得出了许多新的信息熵模型——组合熵、知识熵和粗糙熵等模型。在这些不同的信息熵的模型的基础上，人们提出了不同的属性约简算法。比如，利用数据集上数据中属性之间的互信息，苗夺谦等得出了新的属性约简算法即基于互信息的约简算法。王国胤[11]等提出了基于条件信息熵的属性约简算法，利用条件信息熵来重新定义属性的重要性。梁吉业等利用粗糙熵来重新定义属性的重要性，提出了基于粗糙熵的属性约简算法。

文献[12]中利用相对决策熵的概念来重新定义属性重要性，提出了约简算法FSMRDE。与粗糙集理论中人们所提出的已有信息熵模型不一样的是，FSMRDE约简算法是利用Pawlak提出的粗糙度的定义来重新对相对决策熵进行概括定义的，是对香农信息熵的一种有效扩展。通过实验数据证明，FSMRDE算法不仅可以生成较小的约简，而且所生成的分类器也具有更高的分类精度。特别地，FSMRDE算法的计算开销要小于现有的基于信息熵的属性约简算法，从而使得该算法更适合于处理大规模数据集。

虽然FSMRDE算法具有很多优点，但是文献[12]中所定义的相对决策熵只使用了粗糙度这一概念。粗糙度通常被用来度量知识的完备性，但它却不能有效度量知识的粒度大小，这是因为对任意X⊆U, X的粗糙度只与X的边界区域以及X的上近似有关，缺乏对负区域信息变化的刻画能力。相应地，相对决策熵也不能反映出知识的粒度大小。很多时候，即使知识的粒度变小了(即知识的划分粒度变细)，相对决策熵也不会发生任何变化。这明显是不合理的。因为熵通常表示系统的不确定性，当知识的划分粒度变细，不确定性(即熵)应该减少。为了避免上述问题，有必要将知识粒度这一概念引入相对决策熵中。本文将采用苗夺谦等所提出的知识粒度计算公式，将知识粒度与相对决策熵结合在一起，利用知识粒度来刻画知识的粒度大小，并采用粗糙度来度量知识的完备性，从而得到粒度决策熵这一新的信息熵模型。因此，本文所提出的粒度决策熵模型对于粗糙集中数据集的知识粒度大小和知识的完整精确性都能够进行很好的度量。因此，它是对相对决策熵的一种有效扩展。

本文将基于粒度决策熵来定义属性重要性，并由此提出一种新的属性约简算法ARGDE。与文献[11]中的条件信息熵的算法相比较，虽然都运用了知识熵的概念，但是算法的理论出发点是不一样的。文献[11]中，条件信息熵的算法是在决策属性集对条件属性集的条件熵的基础上提出的，而在本文中ARGDE属性约简算法是建立在条件属性和决策属性的粒度决策熵的基础之上的，以粒度决策熵的变化量作为条件属性对于决策的重要度，并且以此作为启发式信息提出粒度决策熵模型。

通过证明粒度决策熵在约简过程中具有非严格单调性，因此能够确保本文所提出的粒度决策熵模型在粗糙集的属性约简过程中具有精确的合理性。另一方面，为了提高ARGDE算法的计算性能，在该算法中引入了计数排序以及增量式学习的思想，其目的就是在属性约简的过程中使得粒度决策熵ARGDE算法能够拥有更好的计算结果，提高约简算法的效率，与现在已有的约简算法相比较，ARGDE约简算法能够取得较好的计算性能。

1 粗糙集中的有关理论介绍

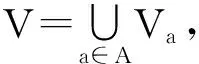
把信息表中的非空有限属性集A分为不相交的2个属性集，一个是属性集C，称为条件属性；一个是属性集D，称为决策属性。这种划分条件属性集和决策属性集的信息表称为决策表，简记为DT=(U, C, D, V, f)。

定义2不可分辨关系[1-2]。对于决策表DT=(U, C, D, V, f)中的任意属性子集B⊆C∪D，由属性集B所确定的一个不可分辨关系IND(B)定义如下：

IND(B)={(x,y)∈U×U:∀a∈B(f(x,a)=f(y,a))}

可以证明，IND(B)是U上的一个等价关系。等价关系IND(B)把决策表中的论域U划分为多个等价类，所有这些等价类的集合就构成U的一个划分，记为U/IND(B)或U/B。

定义3上、下近似[1-2]。给定决策表DT=(U, C, D, V, f)，对任意属性子集B⊆C∪D和对象子集X⊆U, X的B-上近似和B-下近似分别被定义为：

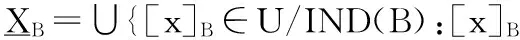
定义4粗糙度[1-2]。给定一个决策表DT=(U, C, D, V, f)，对于任意的属性子集B⊆C∪D和对象子集X⊆U(X≠Φ)，定义X的B-粗糙度如下：

为了度量知识划分的粒度大小，苗夺谦等首次提出了知识粒度的计算公式，具体定义如下。

定义5知识粒度[13]。给定一个决策表DT=(U, C, D, V, f)，对于任意的属性子集B⊆C∪D，如果U/IND(B)={X1,X2,…,Xt}，则U/IND(B)的知识粒度被定义为：

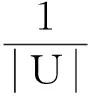
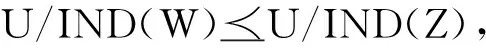
2 粒度决策熵

本文在文献[12]中所提出的相对决策熵模型基础上，在粗糙集中定义一种新的信息熵模型——粒度决策熵，并对粒度决策熵的基本性质进行分析。与粗糙集中现有的信息熵模型不同，粒度决策熵采用粗糙集中的粗糙度以及知识粒度进行定义。粗糙度是粗糙集中的一个重要概念，主要用来度量知识的完备性，而知识粒度则可以度量知识的粒度大小。因此，有必要将这2种知识度量机制结合在一起，从而设计出一种更加全面的信息熵模型。

定义6粒度决策熵。给定决策表DT=(U,C,D,V,f)，令U/IND(D)={Y1,Y2,…,Ym}为IND(D)对U的划分。对任意B⊆C，令U/IND(B)={X1,X2,…,Xt}为IND(B)对U的划分，将D在关系IND(B)下的粒度决策熵GDE(D,B)定义为：

从定义6可以看出，粒度决策熵同时使用粗糙度和知识粒度来进行定义，其中前者可以度量知识的完备性，而后者可以度量知识的粒度大小。将这两者有机地结合起来是非常有意义的，为后续的属性约简提供了一种更加全面的属性重要性度量机制。

下面，给出粒度决策熵的一些基本性质。

定理2给定决策表DT=(U,C,D,V,f)，其中U={x1,x2,…,xn}。令划分U/IND(D)={Y1,Y2,…,Ym}，对任意B⊆C，粒度决策熵GDE(D,B)满足以下性质：

2)当U/IND(B)={{x1},{x2},…,{xn}}时，GDE(D,B)得到最小值；

3)当U/IND(D)={{x1},{x2},…,{xn}}并且U/IND(B)={U}时，GDE(D,B)得到最大值。

证明：

当B为U上的论域关系时：

2)当U/IND(B)={{x1},{x2},…,{xn}}时，由定义3可知，对任意的Yi∈U/IND(D)(1im),Yi的B-上近似和B-下近似都等于Yi自身，从而使得属性集B的粗糙度又由于因此，可以得出GDE(D,B)=0。在此情形下，GDE(D,B)得到最小值0。

3)当U/IND(D)={{x1},{x2},…,{xn}}并且U/IND(B)={U}时，由定义3和定义4可知，对于任意Yi∈U/IND(D)(1im)，ρB(Yi)=1并且知识粒度由于因此，可以得出GDE(D,B)=m=n。在此情形下，GDE(D,B)得到最大值n。

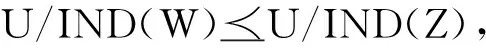
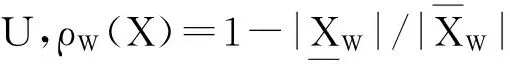
推论1给定决策表DT=(U,C,D,V,f)，对任意W⊆C,Z⊆C，如果W⊇Z，那么GDE(D,W)GDE(D,Z)。

定义7基于粒度决策熵的属性重要性。给定决策表DT=(U,C,D,V,f)，对于任意B⊆C和a∈C-B，将属性a在决策表DT中相对于B和D的重要性定义为：

Sig(a,B,D)=GDE(D|B)-GDE(D|B∪{a})

3 基于粒度决策熵的属性约简算法ARGDE

由于在属性约简的过程中要对属性集B对于论域U的划分进行很多次的计算，因此为了使本文约简算法的时间复杂度和空间复杂度能够降低，利用一种新的理论方法即计数排序的方法来解决这问题。

为了进一步降低算法ARGDE的计算复杂度，首先提出一种增量式计算划分U/IND(B)的算法。

算法1增量式计算U/IND(B)

输入：给定的决策表DT=(U,C,D,V,f)，任意B⊆C∪D，以及之前计算出的划分U/IND(B-{a})={E1,E2,…,Ek}，其中a∈B。

输出：U/IND(B)。

Step1初始化：令U/IND(B)=Φ。

Step2对任意1ik，循环执行：

Step2.1采用计数排序的方法计算划分Ei/IND({a})，其中Ei∈U/IND(B-{a})；

Step2.2令U/IND(B)=U/IND(B)∪Ei/IND({a})。

Step3返回U/IND(B)。

在最坏的情况下，算法1的时间复杂度和空间复杂度都为O(|U|)。

通常，如果采用计数排序的方法来计算划分U/IND(B)，则其时间复杂度为O(|U|×|B|)。然而，在算法1中，为了进一步降低计算U/IND(B)的时间开销，充分利用了之前已经计算出的结果U/IND(B-{a})={E1,E2,…,Ek}，从而使得计算U/IND(B)的时间复杂度仅为O(|U|)。

算法2粒度决策熵GDE

输入：给定的决策表DT=(U,C,D,V,f)，任意B⊆C，以及3个划分：U/IND(B)={X1,X2,…,Xt},U/IND(D)={Y1,Y2,…,Ym}和U/IND(B∪D)。

输出：粒度决策熵GDE(D,B)。

Step1初始化：对任意1it,令flag[i]=F，并且对任意Xi∈U/IND(B)，令I(Xi)表示Xi的编号。

Step2对任意x∈U，分别利用划分U/IND(B)和U/IND(B∪D)来计算等价类[x]B和[x]B∪D的势。

Step3对任意1jm，循环执行：

Step3.1令number1=0；

Step3.2对任意x∈Yj，若|[x]B∪D|=|[x]B|并且flag[I([x]B)]=F，那么令：

number1=number1+|[x]B|

flag[I([x]B)]=T

Step3.3令LA[j]=number1。

Step4对于任意1it，令flag[i]=F。

Step5对于任意1jm，循环执行：

Step5.1令number2=0；

Step5.2对任意x∈Yi，若flag[I([x]B)]=F，则令：

number2=number2+|[x]B|

flag[I([x]B)]=T

Step5.3令UA[j]=number2；

Step5.4对任意x∈Yi，若flag[I([x]B)]=T，则令flag[I([x]B)]=F。

Step7对任意1jm，循环执行：

Step7.1令ρB(Yj)=1-(LA[j]/UA[j])；

Step7.2令GDE(D,B)=GDE(D,B)+ρB(Yj)log2(ρB(Yj)+1)。

Step8令GDE(D,B)=GK(B)×GDE(D,B)。

Step9返回GDE(D,B)。

在最坏的情况下，算法2的时间复杂度和空间复杂度均为O(|U|)。

算法3ARGDE

输入：决策表DT=(U,C,D,V,f)。

输出：约简RED。

Step1初始化：令RED为空集，Core为空集。

Step2利用计数排序的方法计算划分U/IND(C),U/IND(D)和U/IND(C∪D)。

Step3利用算法2计算粒度决策熵GDE(D,C)。

Step4对于任意a∈C，反复执行：

Step4.1利用计数排序的方法计算划分U/IND(C-{a})和U/IND((C-{a})∪D)；

Step4.2利用算法2计算粒度决策熵GDE(D,C-{a})；

Step4.3如果GDE(D,C)≠GDE(D,C-{a})，则令Core=Core∪{a}。

Step5令RED=Core表示当前的约简。如果RED为空集，则令TEM=GDE(D,C)+1；否则，先计算划分U/IND(RED)和U/IND(RED∪D)，然后，再利用算法2计算GDE(D,RED)，并且令TEM=GDE(D,RED)。

Step6若GDE(D,C)≠TEM，则循环执行：

Step6.1对任意a∈C-RED，循环执行：

Step6.1.1基于U/IND(RED)和U/IND(RED∪D)，增量式计算U/IND(RED∪{a})和U/IND(RED∪{a}∪D)；

Step6.1.2利用算法2来计算GDE(D,RED∪{a})，从而得到属性a的重要性Sig(a,RED,D)；

Step6.2从C-RED中选取属性重要性最大的属性b(若有多个，则随机选取一个)；

Step6.3令TEM=GDE(D,RED∪{b}),RED=RED∪{b}。

Step7返回约简RED。

算法3不仅采用了计数排序的方法来计算划分U/IND(B)(其中，B⊆C)，而且还采用了增量式方法，从而使得其计算开销非常小。

在最坏的情况下，算法3的时间复杂度为O(|C|2×|U|)，空间复杂度为O(|C|×|U|)。

4 实验结果

为了能够得出粒度决策熵的属性约简算法对于现有的其他约简算法的性能比较结果，在数个UCI数据集上做了实验对比[14]：1)Tic-tac-toe endgame (Tic); 2)Wisconsin breast cancer (Breast); 3)Zoo; 4)Mushroom (Mush); 5)Congressional voting records (Vote); 6)Lymphography (Lymph); 7)Soybean-small (Soyb)。这7个数据集的详细描述如表1所示。

表1 UCI数据集

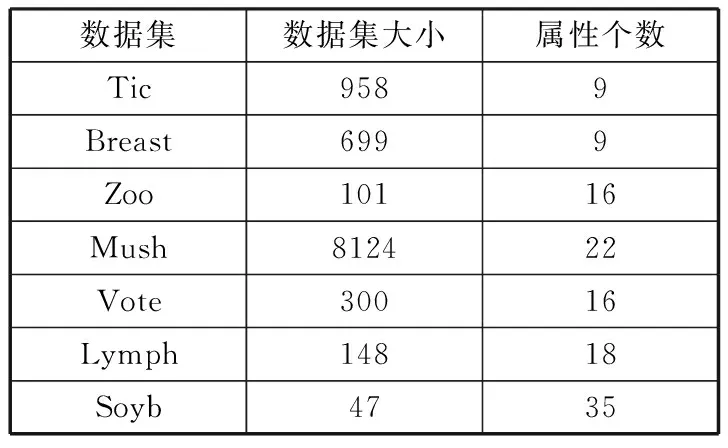
数据集数据集大小属性个数Tic9589Breast6999Zoo10116Mush812422Vote30016Lymph14818Soyb4735

ARGDE约简算法的具体实现主要是采用Java语言，在实验的过程中所用到的硬件环境具体如下：2.5 GHz Intel处理器，8.0 GB内存。在上述7个UCI数据集上，分别比较POSAR(基于正区域的约简算法)[15]、DISMAR(基于分辨矩阵的约简算法)[16]、CIQ(基于条件信息量的约简算法)[17]、GAAR(基于遗传算法的约简算法)[11]以及PSORSAR(基于粒子群优化和粗糙集的约简算法)[18]与本文算法(ARGDE)的性能。对于算法POSAR，DISMAR，CIQ，GAAR和PSORSAR，它们的实验结果可以从文献[18]中得到。

首先，利用数据挖掘平台Weka对数据进行预处理，采用等宽区间(Equal Width Binning, EW)离散化算法对7个数据集进行离散化，其中区间数设置为5。然后，利用不同的约简算法在各个离散化之后的数据集上计算约简，同时对于不同算法得出的约简结果进行比较，表2罗列了不同的属性约简算法在数个不一样的数据集合上的约简比较结果。

表2 各属性约简算法的约简结果对比

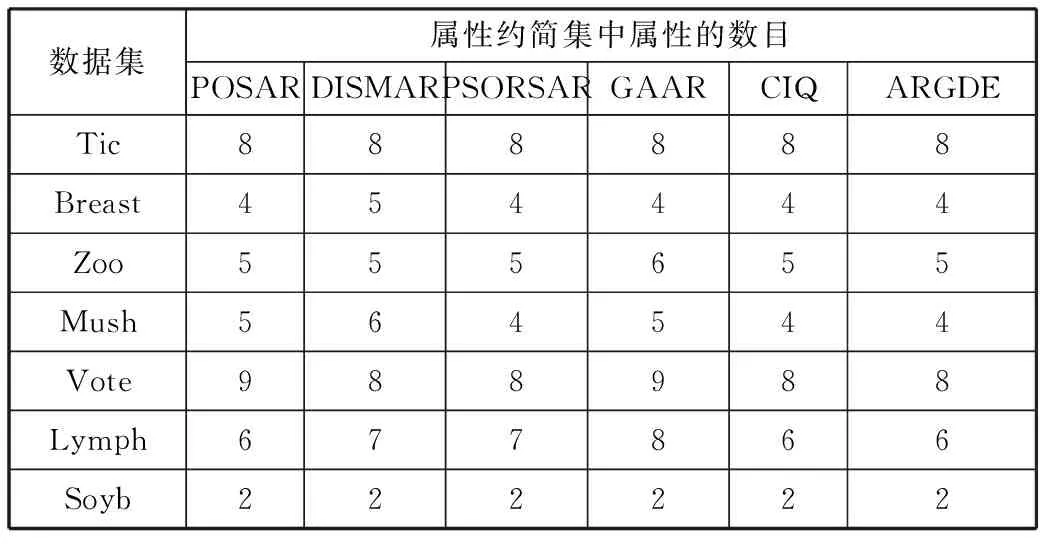
数据集属性约简集中属性的数目POSARDISMARPSORSARGAARCIQARGDETic888888Breast454444Zoo555655Mush564544Vote988988Lymph677866Soyb222222

从表2可以看出，在所有的数据集上，ARGDE算法都能够获得最小约简。因此，从约简的大小来看，ARGDE算法的性能要优于现有的算法。

下面比较不同约简算法的分类精度。本文采用Wang等人所提出的实验验证做法，也就是在实验中当要度量每一个属性约简结果的分类精度时，利用Wang等人提出的十折交叉实验的做法来验证，然后采用RSES系统中的LEM2算法来提取规则，再用提取的这些规则对要进行测试的数据集进行测试实验(如果在测试的过程中出现了冲突，可以通过RSES系统中的Standard Voting方法来解决出现的冲突问题)[19]。关于分类精度具体的实验结果如表3所示。

表3 各属性约简算法的分类精度对比

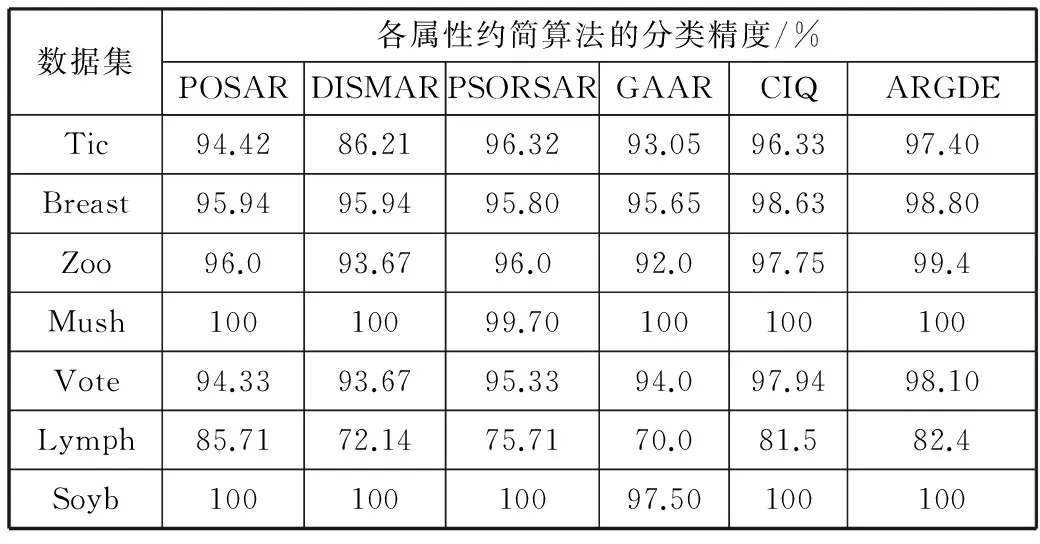
数据集各属性约简算法的分类精度/%POSARDISMARPSORSARGAARCIQARGDETic94.4286.2196.3293.0596.3397.40Breast95.9495.9495.8095.6598.6398.80Zoo96.093.6796.092.097.7599.4Mush10010099.70100100100Vote94.3393.6795.3394.097.9498.10Lymph85.7172.1475.7170.081.582.4Soyb10010010097.50100100

从表3中可以得出，相较于其他5种约简算法，除了Lymph数据集以外，ARGDE算法在大多数数据集上都能取得最高的分类精度。这表明，从分类性能的角度，ARGDE算法也要优于现有的算法。

通过实验可以发现，在Lymph数据集上，ARGDE算法要比POSAR算法的分类性能低一些，这是因为在Lymph数据集中有多个离群点，这些离群点的存在影响了ARGDE算法的分类性能。而对于POSAR算法，所受的干扰要小一些。所以，POSAR算法的分类精度要比ARGDE算法高一些。针对这一问题，可以考虑在进行属性约简之前，利用离群点检测的方法把离群点找出来，尽量避免离群点对ARGDE算法的分类性能的影响。

5 结束语

本文将知识粒度的概念引入相对决策熵中，从而得到了有关粒度决策熵的新模型。在粒度决策熵的基础上，对属性重要度这一概念进行了重新的概括总结。同时，依据粒度决策熵的模型得出了新的有关属性约简的ARGDE算法。ARGDE算法由于采用了增量式学习和计数排序的思想，其计算开销要小于现有的算法。通过在多个UCI数据集上的实验，验证了ARGDE算法的性能。相对于现有的约简算法，本文提出的ARGDE算法在属性约简结果和算法的分类精度方面都能取得更好的结果。一方面，ARGDE算法能够得到比较小的属性约简集；另一方面，在属性约简的分类性能比较的过程中也能够取得比较好的结果。

在接下来的工作中，主要是考虑把粒度决策熵ARGDE算法应用到模糊粗糙集或邻域粗糙集中，设计出新的算法，可以对粗糙集中连续型的数据集进行直接处理，而不是在对数据进行离散化后才可以对数据进行进一步的处理，提高算法的效率，优化算法的性能。

参考文献：

[1] Pawlak Z. Rough sets[J]. International Journal of Parallel Programming, 1982,11(5):341-356.

[2] Pawlak Z. RoughSets: Theoretical Aspects of Reasoning About Data[M]. Dordrecht: Kluwer Academic Publishers, 1991.

[3] 张文修,吴伟志,梁吉业,等. 粗糙集理论与方法[M]. 北京:科学出版社, 2001.

[4] 冯林,罗芬,方丹,等. 基于改进扩展正域的属性核与属性约简方法[J]. 山东大学学报(理学版), 2012,47(1):72-76.

[5] 申雪芬,谢珺,刘海峰,等. 一种改进的基于相对正域的增量式属性约简算法[J]. 广西师范大学学报(自然科学版), 2013,31(3):45-50.

[6] 杨波,徐章艳,舒文豪. 基于差别矩阵的完备属性约简算法[J]. 计算机工程, 2011,37(16):51-53.

[7] 葛浩,李龙澍,杨传健. 基于简化差别矩阵的增量式属性约简[J]. 四川大学学报(工程科学版), 2013,45(1):116-124.

[8] 葛浩,李龙澍,杨传健. 基于差别集的启发式属性约简算法[J]. 小型微型计算机系统, 2013,34(2):380-385.

[9] 陈媛,杨栋. 基于信息熵的属性约简算法及应用[J]. 重庆理工大学学报(自然科学), 2013,27(1):42-46.

[10] 吕林霞,赵锡英,唐占红. 一种基于信息熵的信息系统属性约简算法[J]. 自动化与仪器仪表, 2013(5):197-199.

[11] 王国胤,于洪,杨大春. 基于条件信息熵的决策表约简[J]. 计算机学报, 2002,25(7):759-766.

[12] Jiang Feng, Sui Yuefei, Zhou Lin. A relative decision entropy-based feature selection approach[J]. Pattern Recognition, 2015,48(7):2151-2163.

[13] 张伟,徐章艳,王晓宇. 一种结合概率启发信息和知识粒度的属性约简算法[J]. 计算机应用与软件, 2013,30(7):43-45.

[14] Hettich S, Bay S D. The UCI KDD Archive[DB/OL]. http://kdd.ics.uci.edu, 1999-01-10.

[15] 江峰,王莎莎,杜军威,等. 基于近似决策熵的属性约简[J]. 控制与决策, 2015,30(1):65-70.

[16] Hu Keyun, Lu Yuchang, Shi Chunyi. Feature ranking in rough sets[J]. AI Communications, 2003,16(1):41-50.

[17] 李鸿. 基于条件信息量的知识相对约简算法[J]. 中国矿业大学学报, 2005,34(3):378-382.

[18] Wang Xiangyang, Yang Jie, Teng Xiaolong, et al. Feature selection based on rough sets and particle swarm optimization[J]. Pattern Recognition Letters, 2007,28(4):459-471.

[19] Skowron A, Bazan J, Son N H, et al. RSES 2.2 User’s Guide[EB/OL]. http://logic.mimuw.edu.pl/rses, 2005-01-19.