核心企业主导集成化供应链模型的一般性研究

（中铁物贸集团有限公司成都分公司，四川 成都 610032）

1 引言

在核心企业主导集成化供应链中，核心企业通过制定供应链运作相关标准，对各节点企业约束管理，使各节点协同运作以期提高效率[1]。关于集成化供应链的研究成果表明，集成化供应链效率高于传统松散结构的供应链[2]。在供应链集成化模型研究方面，学者对模型中所使用的销售函数、成本函数等无法客观度量的因素以确定的形式给出[3]，如成本关于服务品质的函数以二次函数表示[4]。有研究避开函数具体形式，对函数抽象化处理，探讨具有某一特征的函数族类的模型，讨论两个节点企业集成化供应链的情况[5]，而实际商业生产运作环节，多节点企业构成的供应链更为常见，本文以三节点企业供应链作为研究对象，针对该结构供应链不同决策思维模式下的服务品质和利润进行研究。

2 问题描述与假设

2.1 问题描述

供应链中，制造商以单位生产成本p0生产某产品。核心企业为批发商，以单位价格p1购买该产品，并且以单位价格p2批发给零售商。零售商以价格p3销售给消费者，如图1所示。

图1 三节点企业供应链结构

2.2 假设

假设1 供应链中节点企业均为经济人，市场价格由卖方基于生产成本、竞争对手等因素制定。

假设2 供应链整体服务品质与各节点企业额外成本的函数可以表示为：，且满足，其中ci为供应链中各节点企业为提升服务品质而投入的额外成本，i=1,2,3。

假设3 供应链整体销量可由函数q(x)表示，且满足，其中x为服务品质。

3 零和博弈与非零和博弈思维模式下的模型

本节讨论两种思维模式下的供应链，以模型为基础，在服务品质和利润方面进行对比分析。

3.1 零和博弈下核心企业主导的供应链模型

批发商在集成供应链中扮演核心企业角色，在利润分配方面结合固定额度分配与绩效提成，各节点企业忽略内部交易，以整体利润为基础分配。核心企业分配整体销售总利润的α1和固定金额为ω1给制造商，分配整体销售总利润的α3和固定金额ω3给零售商。由此确定制造商获取利润总额可表示为：s1=α1(p3-p0)q(x(c1,c2,c3) )+ω1-c1；批发商获取利润总额为：s2=α2(p3-p0)q(x(c1,c2,c3) )-ω1-ω3-c2；零售商获取利润总额为：s3=α3(p3-p0)q(x(c1,c2,c3) )+ω3-c3，其中α1+α2+α3=1，0＜αi＜1,i=1,2,3。

ci为各节点企业投入成本，由此判定为自有决策量，基于假设1可知各节点企业追求利润最大化基本原则为，具体为：

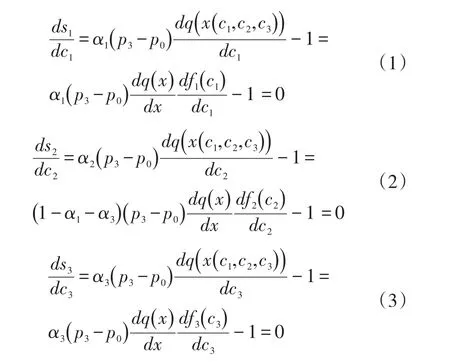
α1,ω1,α3,ω3均由核心企业决定，因此核心企业在分配利润时会基于自身利润最大化视角决策。s2为关于α1,ω1,α3,ω3,c2变量的函数。目标函数关于ω1,ω3单调递减，因此批发商分配固定利润时取其下限,即 可 ，即 有 ：αi(p3-p0)q(x(c1,c2,c3) )+ωi-ci≥j*ci，其中j为制造商和零售商可接受的最低利率，=(1 +j)*ci-αi(p3-p0)q(x(c1,c2,c3) )，获得利润总额为j*ci。

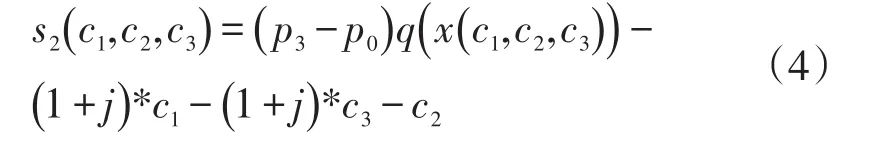
由公式（1）、（3）可得，c1为关于α1的单调递增函数，c3为关于α3的单调递增函数，因此核心企业确定的α1,α3能够间接控制供应链中其他企业成本函数-c1,c3。由公式（4）得知模型退化为求解s2(c1,c2,c3)最大值，其中s2为c1,c2,c3的凸函数，即求解下述方程组可求最大值对应解c1*,c*2,c*3。

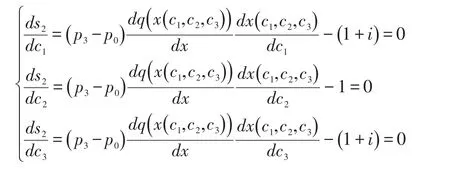
由上述得知，核心企业在确定αi时，满足下述等式即可：

对于完全离散的供应链，节点企业彼此之间相对孤立，各节点企业利润为si=(pi-pi-1)q(x( 0,0,0 ) )，这类供应链属于特殊情况，即，ωi=0,ci=0。

3.2 非零和博弈下核心企业主导的供应链模型

基于非零和博弈思想，核心企业与其他节点企业间存在价值渗透，集成完全协同的供应链，利用契约确定分配，供应链整体以利润最大化为共同目标，即求：Max{s(c1,c2,c3) }，其中整体利润s(c1,c2,c3)具体可表述为以下形式：

显然s(c1,c2,c3)为凸函数，求解下述方程组可求得利润最大值对应解。

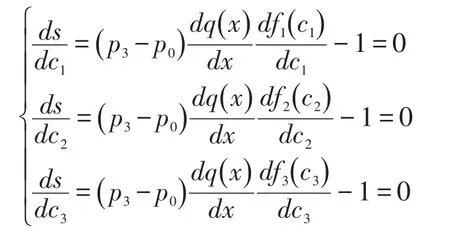
3.3 模型对比

3.3.1 对比和。在假设中服务质量函数和销售量函数为具有相应性质的函数类，而非具体函数，与不能直接给出具体表达式，因此不能直接比较和大小。在此情况下，视c为固定值，即视为两k种模型下ck数值保持不变，其中k≠i。对比两类模型，零和博弈情况下参考等式（1）、（2）、（3）有：。非零和博弈下参考公式（5）对应的方程组有：。显然有，在此不等式基础上，确定为关于ci的增函数或者减函数即可对比两者大小。针对求导，可得：

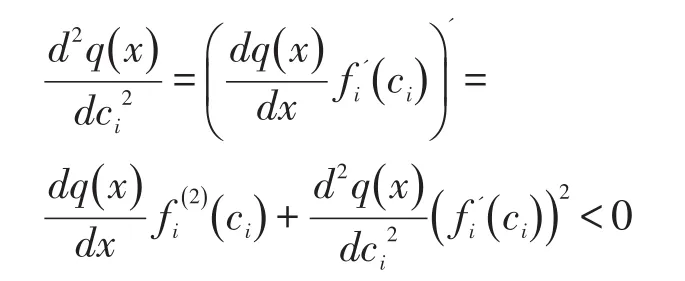
3.3.2 对比整体利润。供应链整体利润函数为(p3-p0)q(x(c1,c2,c3))-c1-c2-c3，显然零和博弈模式下额外成本对应的利润为，非零和博弈模式下额外成本对应 的利 润 为。两者均为利润函数的一个值，前者为某一特定空间中—古诺-纳什均衡曲面中的最优解，而后者可行域包含该曲面，其为更宽泛空间下的最优解。

以下是关于该曲面推导过程：

现在令供应链下游节点企业的提成系数α3为不同特定值，即有α3取不同数值时，核心企业在此条件下使得自己利润最大化（如图2所示）：当α3=α3A1，则模型的可行域退化为古诺-纳什均衡曲面均衡曲线S1A1P1[6]；当则模型的可行域退化为古诺-纳什均衡曲面均衡曲线S2A2P2；当则模型的可行域退化为古诺-纳什均衡曲面均衡曲线SnAnPn。

每一个α3∈(0,1)对应一条古诺-纳什均衡曲线，则所有古诺-纳什均衡曲线可构一个古诺-纳什均衡曲面h(c1,c2,c3)=0，该曲面上每一个点均为古诺-纳什均衡点。若非零和博弈模式下可行域为C，则零和博弈模式下可行域域为{c|c∈C,h(c)=0} ，显然{c|c∈C,h(c)=0}⊆C，因此可以得出以下不等式：

图2 古诺-纳什均分曲面推导图

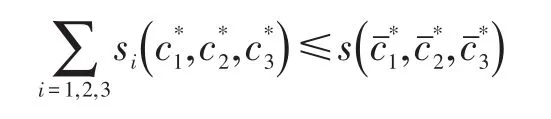
由此断定，非零和博弈模式下的供应链整体利润高于零和博弈模式下的利润。

4 基于模型的实例研究

某物贸集团是一家央企股份公司的全资子公司，为实现股份公司区域集采战略而成立，公司经营范围包含石油、矿石、钢材、水泥、钢轨等。该物贸集团旗下设有八大子分公司负责推进系统内区域集采，其中西南地区一分公司在集采方面业绩突出，规模较大。分公司在推进集采过程中，以钢材、水泥作为主要业务板块，石油、钢轨、装饰装修等业务作为补充。钢材业务营业额突出，利润价值大，占用资金多，主要含有螺纹钢、盘螺、盘条和圆钢，螺纹钢比重为92%，是本实例研究的对象。

当前公司构建的货源渠道以钢厂直发为主，供应商发货为辅，销售给项目经理部，业主单位根据项目经理部完成的生产任务划账，故可视项目经理部为零售商，业主单位为消费者。从分公司签署的合同看，螺纹钢从厂家以检斤做为计量方式买入，检尺作为计量方式卖出，结合历史数据和大数定律可以得知磅差均值为3.28%；买入价格和卖出价格为浮动制，以我的钢铁网（http://www.mysteel.com/）当日公布价格为基准，结合合同约定条款进行调整。

基于上述背景，某轨道交通建设业主单位划分生产任务给项目经理部，预期消耗钢材50 000t，项目经理部与物贸公司签署钢材供应合同，实际供应数量与供应过程中服务品质相关，即有数量q(x)=50 000 1+x，其中x为服务品质，当x=0时，供应链的服务品质为无差异状态，仅能完成预期供应量。为提升竞争力，供应链中各节点企业通过提升服务品质增加销售量，通常服务成本占销售成本5%为佳，相应给出成本度量销售量函数：

其中c1，c2，c3分别为供应链中钢厂、物贸公司、项目经理部额外成本。由于钢材价格为波动的，为简化研究，取近期价格相近值4 100元作为基准价进行研究，每吨生产成本约为p0=3 750元；据物贸公司签署的合同表明，其能够在网价基础上取得20元优惠，以每吨p1=4 080元价格以检斤计量方式买入，且钢厂承担运费。在网价基础上每吨优惠50元并外加配送等服务费60元，且以检尺数量售项目经理部，即每吨实际售价为p2=4 110*1.032 8元；据物资部工作人员保守估计，项目经理部每耗费一吨螺纹钢可以获得业主单位4 500元划款，即p3=4 500元，供应链钢材价格具体运作如图3所示。

图3 钢材供应链价格运作图

4.1 完全离散的供应链

当各节点企业之间参考相应市场价格进行交易，服务品质为0，则相应的额外成本为0，供应链整体利润为：3 750万元。

4.2 基于零和博弈思想的供应链

假设钢厂和项目经理部能接受的成本最低回报率为5%，则零和博弈模式下的模型参考公式（4）可知，利润目标函数s(c1,c2,c3)可表示为：

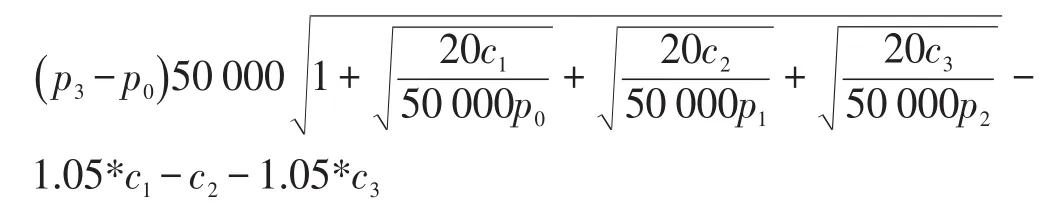
4.3 基于非零和博弈思想下的供应链

非零和博弈模式下参考公式（5），利润目标函数s(c1,c2,c3)可表示为：

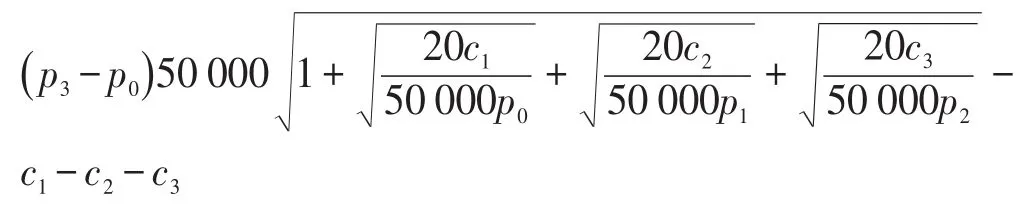
4.4 三种供应链对比

在实际生产运作中，各节点企业通常消极对待提升服务品质，期望通过搭便车提升供应商整体服务品质，因此在额外成本投入方面，节点企业均不超过最佳额外投入，即不超过产品成本的5%，相应约束条件有：，针对该案例中的求解问题，可以采用拉格朗日函数取得相应解析解。本文采取数值方法求解，受蒙特卡洛方法启发，给出一种随机算法求解，表1为实现该方法的伪代码。

表1 随机算法伪代码

结合算法，给出模型结果见表2。

表2 三种供应链各项指标对比 单位：万元

表1结果表明，同完全离散的供应链相比较，整合后的供应链（零和博弈或者非零和博弈模式下的供应链）在总体利润指标上优势突出，整合供应链，实现供应链集成化运作为挖掘利润提供保障。但结果中，钢厂和项目经理的利润对比表明，零和博弈模式下供应链显然不具备可行性，而非零和博弈供应链在平衡利润分配的前提下，是实现供应链整合，提升整体利润的有效途径。并且，同完全离散供应链相比较，各节点企业的额外成本提高，相应的服务品质增加。

5 研究结论

本文通过构造一般性模型研究供应链，研究结果表明非零和模式下供应链与完全离散供应链和零和博弈模式下供应链而言存在着优势，能确保供应链服务品质，提高供应链整体利润。本文在对比服务品质方面，利用数学分析工具证明，在其他节点企业额外成本不变，非零和博弈模式下，该节点企业额外成本增加，供应链整体服务品质提升。两中模式下的总利润对比本质是求同一目标函数最大值，零和博弈的可行域包含于非零和博弈，故后者最优值较大。对于更多节点企业构成的供应链，本文未予研究，多节点模型中，额外成本研究可通过文中数学分析手段完成；总利润比较可通过对比两者可行域包含关系实现。

[参考文献]

[1]陈建华,马士华.供应链整合管理的实现机制与技术解决方案[J].工业工程与管理,2006,(1):24.

[2]徐晶.核心企业主导的集成化供应链管理系统的研究[D].杭州:浙江大学,2006.

[3]蹇明,宗涵,鲁工圆.考虑销售价格变动的服装行业供应链契约研究[J].工业工程,2015,(6):11-17.

[4]付红勇.订单农业模式下考虑天气影响的农产品供应链协调[D].重庆:重庆大学,2013.

[5]刘建.核心企业主导的生猪供应链整合分析[D].成都:西南交通大学,2016.

[6]中国精算协会.经济学基础[M].北京:中国经济出版社,2010.