连续排水边界下一维均质地基的固结性状分析

2018-05-09张国英李勇义

现代矿业 2018年4期

张国英李勇义李康

(1.广西大学土木建筑工程学院;2.嘉兴锦大工程管理咨询有限公司)

土的固结是土力学的重点问题之一，主要是由固结方程、初始条件、边界条件3个部分组成，而且与土的变形、强度、渗透有着紧密的联系。自Terzaghi[1]在一系列假设简化的条件下建立一维固结理论之后，固结理论的研究得到了快速的发展，随后许多学者也相继研究了一维、二维、三维等各种不同类型的固结问题[2-4]，对固结理论的发展有重要的意义。

但是许多研究工作都是基于现有固结问题中边界条件不满足初始条件这一矛盾求解的。针对这一问题，梅国雄[5]等提出了从透水到不透水的连续排水边界条件，能够很好地解决固结求解中存在的问题，从而对现有固结理论中边界条件不满足初始条件这一问题进行修正，本文基于此连续排水边界条件开展研究。

1 连续排水边界

以Terzaghi一维固结理论为例，

(1)

其求解初始条件为

u(0,z)=p，

(2)

边界条件为

顶面透水时

u(t,0)=0

(3)

底面不透水时

(4)

式中，u为孔隙水压力，Pa；t为固结时间，d；Cv为固结系数，m2/d;p为骤加荷载,Pa;H为土层厚度,m。

从式(2)可以得到

u(0,0)=p.

(5)

从式(3)可以得到

u(0,0)=0 .

(6)

从式(5)和式(6)可以看出方程的边界条件不满足初始条件，即边界条件和初始条件矛盾。

同时,Terzaghi给出解答如下：

(7)

当z=0时，根据其解答可以得出u(t,0)，这与初始条件u(z,0)也是矛盾的。

基于此，梅国雄[5]等提出一种连续排水边界条件：

u(t,0)=pe-bt,

(8)

式中,u(t,0)为t时刻边界z=0的孔压,Pa；p为荷载，Pa；b为反映边界排水性能的参数，d-1，并且b>0，b越大，边界的排水性能越好。

该边界条件能够很好地和初始条件统一，使其更接近实际的排水情况。

2 固结方程及其解答

2.1 连续排水边界下的解答

地基边界的排水条件取为连续排水边界，分为单面连续排水边界和双面连续排水边界，其余假设和Terzaghi一维固结理论相同。饱和软土层的厚度取H，渗透系数为k，土的体积压缩系数为mv，水的容重为γw。本文按照单面排水计算，双面排水只需用H/2代替单面排水情况式中的H即可[6]。地基一维固结模型见图1。

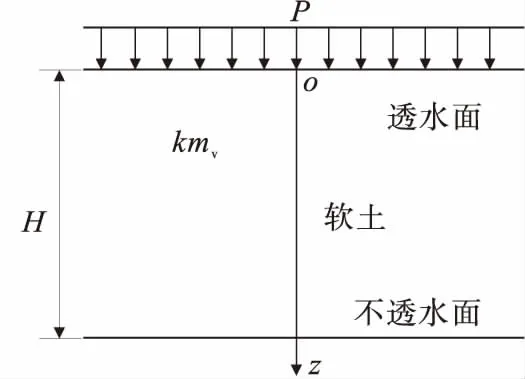
图1 地基一维固结模型

图1中一维固结方程为

其求解初始条件与边界条件为

(9)

为了方便方程的求解，令

u=v+pe-bt，

(10)

代入原方程以及初始条件和边界条件中可以得

(11)

其中，

f(t)=bpe-bt,

(12)

(13)

将定解问题的解v(t,z)和自由项f(t)按关于z的固有函数展开为傅立叶级数,即

(14)

(15)

(16)

将式(14)、式(15)代入式(11)中可得

(17)

求解以上一阶常微分方程可得

(18)

(19)

然后将式(18)代入式(14)中可得v(t,z)，再代入式(10)中可求得u(t,z)的一般解答式:

(20)

当b→∞ 时,式(20)中孔压解答可退化为

(21)

即为Terzaghi固结解析解。

固结度解答为

(22)

沉降解答为

(23)

从解析式可以看出,固结度和沉降不仅与固结系数、排水距离有联系，还与边界的排水性能有关。

2.2 解答的分析

为了验证文中解析解的正确性，编制了相关计算程序，将本文解答和Terzaghi解答进行对比分析，所用土体参数γ=18.1 kN/m3，H=10 m，μ=0.3，E=10 MPa，荷载p=100 kPa，水的容重γw=10 kN/m3。

由连续排水边界的特点可知，当b无穷大时，连续排水边界即退化为一般排水边界。不同时间因数时土层的孔压曲线变化见图2。可以得出，当本文计算时b取较大值10 000 d-1时，本文解答就已经与Terzaghi解答的孔压消散曲线重合非常好，这也充分说明了本文推导的解析解及计算程序的正确性。

图2 不同时间因数时土层的孔压曲线

◆—Tv=0.3,b=10 000 d-1时本文解；■—Tv=0.5,b=10 000 d-1时本文解；★—Tv=0.7,b=10 000 d-1时本文解；●—Tv=0.9,b=10 000 d-1时本文解

为了研究本文解答的收敛性情况，选取时间因数Tv=0.5，深度z=5 m处的孔压进行分析，同时取b=0.1d-1，其孔压计算结果见图3。可以得出，固结系数Cv取较小值时的收敛性比取较大值的收敛性好，但是总体上本文解答的收敛性都非常好，基本上取级数前五项就能够满足精度要求。同时可得出，当固结系数Cv取值不同时，孔压也不同，而且固结系数Cv取较小值0.1、0.01、0.001时孔压相差不大，固结系数Cv取较大值10、1时孔压相差很大，这也说明当时间因数一定时，固结系数越大，固结所需的时间越短，b对结果的影响越大。而经典Terzaghi一维固结中,当时间因数相等时，孔压不变，这也和Terzaghi一维固结不一样。

图3 级数项数对孔压的影响

3 参数敏感性分析

3.1 边界参数b对孔压的影响

选取时间因数Tv=0.5，并对连续排水边界参数b取不同值时，计算土层的孔压，其孔压曲线见图4。图4表明，当b取值越大时，土层孔压消散得越快，孔压消散曲线越接近Terzaghi解答孔压消散曲线，而且边界z=0 m孔压不再是零，而是随着时间逐渐减小到零，这也说明了排水边界不再是直接由初始孔压直接突变为零，而是将排水边界与时间建立关系，这对研究孔压消散规律有重要的意义。

图4 b取不同值时土层的孔压曲线

3.2 边界参数b对固结度的影响

图5为不同连续排水边界参数b值地基的固结度随时间因数的变化曲线。图5表明，随着b取值增大，即边界排水性能增加，地基固结速度越快，但是固结速度增加率越来越小。在固结前期，b取值不同，其固结速度相差较大，而在中后期固结度的变化曲线相差不是很大，并且越来越接近Terzaghi固结曲线。

图5 不同b值时地基的固结度曲线

3.3 边界参数b对沉降的影响

图6为不同连续排水边界参数b值地基的沉降随时间的变化曲线。可以看出，b取值越大，地基沉降速度越快，但是沉降增加率随着b值的增大而减小，特别是在地基沉降完成的中后期，b值对沉降影响不大，并且地基的最终沉降量不受b值大小的影响，和Terzaghi固结沉降曲线计算一样，这也说明了本文解答的正确性，边界排水参数b值只影响沉降完成的速度，而不会影响最终的沉