运动中寻定值 变化里觅恒量*
——一道解析几何说题比赛的实录与反思
2018-05-09
● ●
(宁波市教育局教研室,浙江 宁波 315000) (鄞州高级中学,浙江 宁波 315100)
不久前,浙江省宁波市教育局教研室组织了以“核心素养背景下的新高考新学考研讨”为主题的说题比武活动,说题内容选自2017年学考题或高考试题中的某一道题目.每位参赛选手精心准备,说题过程精彩纷呈,引起参会一线教师的浓厚兴趣.笔者选择简约而不简单的2017年4月浙江省数学学业水平考试第24题(解析几何题)为说题内容,以培育学生数学运算、逻辑推理等核心素养为目标,总结归纳处理解析几何中定点、定值问题的通性通法,挖掘蕴含函数与方程、数形结合、设而不求、整体代换等思想方法的说题展示,得到了评委和与会教师的一致好评,获得了一等奖中的第一名.下面把这道解析几何说题的过程和反思整理成文,与各位同行交流,敬请批评指正.

图1
题目已知抛物线C:y2=2px,过点A(1,1).
1)求抛物线C的方程;
2)过点P(3,-1)的直线与抛物线C交于两个不同点M,N(均与点A不重合),设直线AM,AN的斜率分别为k1,k2,求证:k1k2为定值.
1 说解法
第1)小题求曲线方程,因抛物线已定型,利用点在曲线上列方程很方便能求解(其中抛物线方程为y2=x).第2)小题考查直线与抛物线的位置关系.已知两个定点、3条动直线,求证结论是两条动直线斜率积为定值.动中含定,说明3条直线运动时相互牵制,因此问题的关键是在变化中寻求不变的因素,第2)小题有如下3种证法.
2)证法1设lMN:x=t(y+1)+3,M(x1,y1),N(x2,y2),联立方程
得
y2-ty-3=0,Δ>0,
从而
y1+y2=t,y1y2=-t-3,
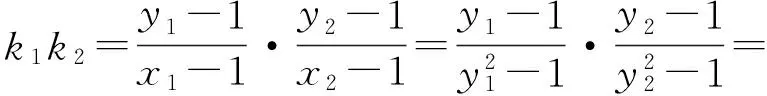
证法2设lAM:y-1=k1(x-1),M(x1,y1),N(x2,y2),联立方程
得
k1y2-y+1-k1=0,
从而
Δ=1-4k1(1-k1)=(2k1-1)2≥0,
可得
同理可得
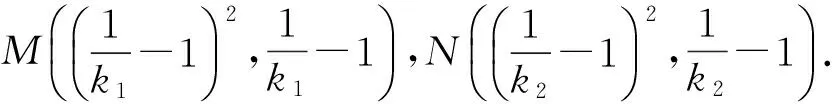
由点M,N,P共线,可得kMN=kMP,即
化简得

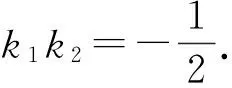
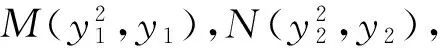
y1y2+y1+y2+3=0,


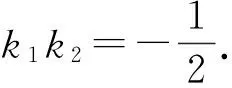
证法1是通性通法,设直线方程,联立方程组,利用韦达定理,利用整体代换思想建立目标与已知的联系,从而得到斜率之积为定值;证法3是优法,是基于抛物线的方程特征使计算优化;证法2把点M和点N的坐标表示出来,对比证法1要复杂一些.因此在教学过程中,教师不仅要让学生学会通性通法,而且更应针对不同的圆锥曲线方程特征,通过对比优化解法,降低运算难度,提高运算准确性.
2 说本质
解题教学的关键是学会解题分析,主要包括解题思路的探求和解题过程的反思.所谓解题思路的探求,就是把“题”作为认识的对象,把“解”作为认识的目标,重点展示由已知条件到未知结论的沟通过程,说清怎样获得题目答案的本质,即完成从认知过程到思路探求的过程[1].本题从条件出发,从3条弦的运动出发寻找动因、刻画动因.
2.1 动因分析
当直线经过一定点时,欲使之运动,可以从两个方面做到:一是使斜率变化;二是让直线过一动点.
2.2 选择刻画动因的量
从斜率变化来看,可设过定点P的直线lMN的方程为x=t(y+1)+3或设过定点A的直线lAM的方程为y-1=k1(x-1).从直线过一动点来看,将点的坐标作为参数.尽管点的坐标是“二元”变量,但因为抛物线的方程特征,可使得“二元”降为“一元”,从所求出发,可证k1k2为定值.解析几何的精髓是用代数解决几何问题,即几何问题代数化,代数问题坐标化.
2.3 构造恒等式
通过构造恒等式来实现以“静”制“动”的目的,利用韦达定理整体代换构造关系式,或者利用点M,P,N共线构造恒等式.
本题解题思路用框图呈现如图2所示.

图2
3 说拓展
一道题目的价值不仅在于该题的解法、结论,而是应“综合全面地看待条件与条件、条件与结论、洞察问题的深层结构”[2].对于这道解析几何题的价值更深刻全面的认识体现在数学深层结构的统一美与和谐美.
3.1 互换条件结论编制成新试题
这道题的条件是动直线过定点,结论是斜率积为定值.从逆命题视角来看,教师可引导学生探究条件和结论互换后的命题是否依旧成立.
改编题已知抛物线C:y2=2px过点A(1,1).
1)求抛物线C的方程;

原题是定值问题,互换结论与条件,即变成定点问题,证明方法与定值问题相似.通过互换条件结论编制新试题使学生了解题目编制的方法,如互换条件结论、普遍化、特殊化、类比、条件重组等,使学生通过学透一题会解一类题目.
3.2 从特殊到一般横向“寻根发芽”
由改编题的定点问题,教师可引导学生回忆抛物线一个定点问题:
定理1已知抛物线C:y2=2px,O是坐标原点,M,N是抛物线C上两个不同的动点,若OM⊥ON,则直线MN恒过定点(2p,0).
对比定理1与改编题,发现定理1的定点问题是改编题更特殊的情况,接着顺势鼓励学生猜想证明是否有一般的结论.



由定理2与定理3,可得:

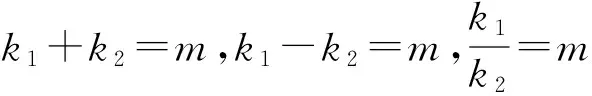
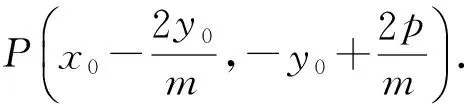
特别地,当m=0时,直线MN不过定点,斜率为定值.
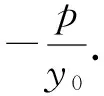

改变抛物线开口方向,可得到不同的结论,引导学生再次探索结果差异的原因,从而推动解题模式的积累和解题经验的生成.
3.3 由“点”及“面”纵向统一和谐
圆锥曲线具有统一性,有统一的定义,在直角坐标系中有统一的方程,研究方法基本一致,通过类比能发现类似的几何特征和基本性质.教师应引导学生在广度上纵向探究一般圆锥曲线的定点、定值问题,是否有如上抛物线探究证明得到的类似结论.在课堂上教师可以通过信息技术辅助探究,用几何画板向学生展示圆锥曲线动态问题中的定点、定值结论.
推广1斜率定积,连线过定点.

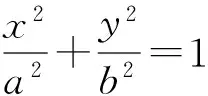

推广2斜率定和,连线过定点.
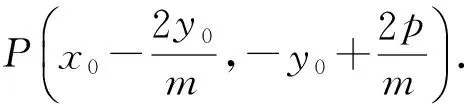
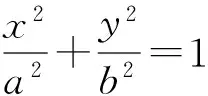

特别地,当m=0时,可得如下定理:
定理8过圆锥曲线上一定点作倾斜角互补的两直线交曲线于另两个交点的连线的倾斜角为定值.
定理8的几何意义为该定点关于轴的对称点处切线方程的斜率为定值.此定理是近几年很多高考题和竞赛题的命题背景知识.
4 说教学价值
“说”的归宿是“教”,“教”的归宿是“学”.通过该题的“教”与“学”,实现解析几何的教学价值:学会“以数解形”“以形助数”,学会把握数形之间的内在联系.教师进行一题式教学时,不仅应反思解题的教学过程,还应反思该题的拓展延伸和教学价值.
4.1 重视运算方法指导,培育学生数学运算素养
解析几何教学是提升数学运算核心素养的一个良好载体,通过本题教学在课堂教学过程中落实培育数学运算核心素养.
1)掌握模型,获取运算经验.
学生在学会解题的过程中需要经历解题思路的探求、解题能力的提高、解题策略的形成、解题模式的提炼四步领悟.在处理解析几何问题时应引导学生掌握通性通法,弄清基本解题思路,获取基本的数学运算经验.
2)转化化归,明确运算方向.
将几何条件转化化归为熟悉的代数式与代数运算,如三点共线转化为斜率相等或向量倍数关系进而转化成坐标关系运算.
3)优化运算策略,提升运算速度.
在解题教学中,教师应注重强调选择恰当的运算策略、灵活的运算途径,通过追问形式,让学生比较运算策略的优劣对于运算结果的影响.在教学过程中,教师不仅要让学生学习通性通法,更应该针对不同的圆锥曲线的方程特征,比较解法优劣,优化解法,学习个性解法,降低运算难度,提高运算准确性.同时,应记住一些结论,事半功倍.
4.2 通过探究拓展的过程,培养学生逻辑推理素养
学东西的最好方式是发现它,而教师的任务是帮助学生学会猜想,学会选择恰当的方法解决或证明问题.教师鼓励学生通过合情推理对抛物线的定点定值性质作了大胆的猜想、探索和验证.同时通过类比,使这些性质在椭圆、双曲线中得到全面推广.这样的探索与研究体现了合情推理在数学研究中的重要作用,同时也让学生感受到圆锥曲线性质的内在统一的和谐美.学生在分析、类比、猜测、证明过程中提升逻辑推理的数学核心素养.
5 结束语
“一叶而知秋,一题一世界”.说题比赛活动不但能提升教师的数学专业水平,而且还能通过一题一课的方式在课堂上落实数学学科的核心素养,可以促使教师研究试题成为自觉的行动.说题给喜欢探讨数学问题的教师提供交流解题教学的一个重要平台.
[1] 罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,2008.
[2] 波利亚.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2011.
[3] 张岚.基于数学核心素养的解析几何教学——谈数学运算能力的提升[J].中学教研(数学),2017(5),27-30.
