基于课程资源视角的数学“长作业”探究*

●

(黄岩第二高级中学,浙江 台州 31800)

什么是数学“长作业”？数学“长作业”是指完成时间较长的数学作业，可能需要好几天甚至好几个星期，作业的内容主要来自教科书，如：一个问题的推广，或是课后一个思考题，或是一类问题的专题总结……，一般需要学生合作探究来完成[1].

课程资源也称教学资源，就是课程与教学信息的来源，或者指一切对课程和教学有用的物质和人力.一线教师极少参与课程资源开发，实施空间仅局限于课堂，内容偏重于课本，结构单一，不利于学生发展，因此，我们有必要立足教学实践开发课程资源.下面笔者基于课程资源视角谈谈数学“长作业”探究.

1 案例回放

1．1 提供原问题

笔者回忆自己以前教学双曲线定义的过程：首先，通过对椭圆定义的回忆、类比，得出双曲线定义——平面内与两个定点F1,F2的距离的差的绝对值是常数(小于|F1F2|)的点的轨迹叫做双曲线，并对定义中的“绝对值”“常数(小于|F1F2|)”等作变式教学，学生对双曲线的定义有了较深刻的理解；然后，利用双曲线定义来解决问题.

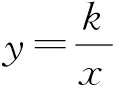
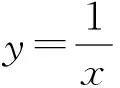
1．2 讨论原问题

上课伊始，首先按照往常分成8个学习小组，给出问题先在小组交流，充实改进达成共识后，再由各组选出代表在班上交流.

方法1利用双曲线定义判断.

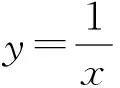
图1

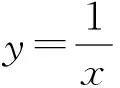
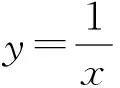
下面就P(x,y)在第一或第三象限分别讨论之，均得到

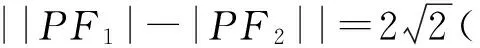
问题得证.

(此方法8个小组都顺利得出.)

方法2利用双曲线第二定义.

生2：我们组还运用双曲线第二定义进行判断，具体思路为：寻找一条定直线l，使曲线上任一点P到定点F的距离与到这条定直线l的距离之比e是大于1的常数.

图2

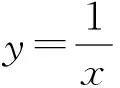
又点P到直线l的距离为

则

问题得证.

(此方法只有5个小组得出.)

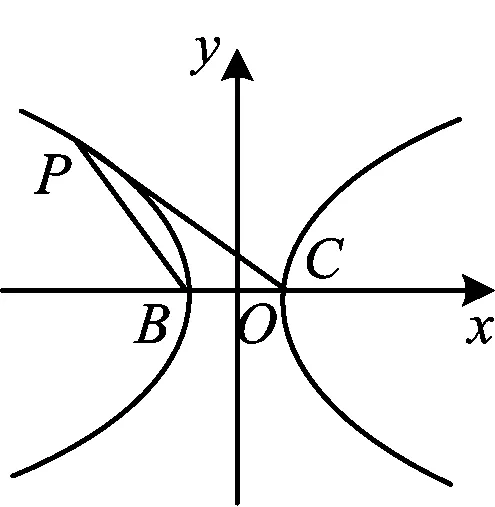
图3

方法3利用双曲线轨迹题的结论.

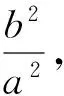
与方法1类似，可得B(-1,-1),C(1,1)是双曲线的顶点，但它们的连线是直线y=x，不是原来的x轴.因此将上述的思路修正为：设B,C是平面内两个定点，P为平面内一动点，直线BC到PB,PC的角分别为α,β，若tanαtanβ是大于0的常数，则点P的轨迹为双曲线(如图4).

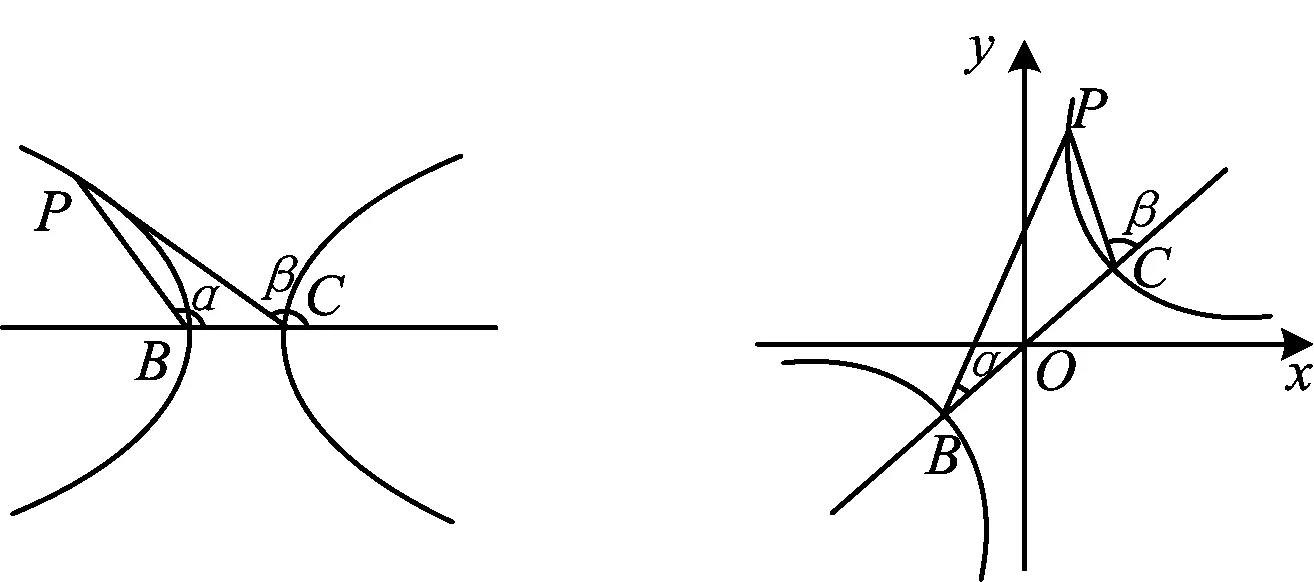
图4 图5

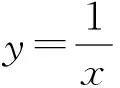
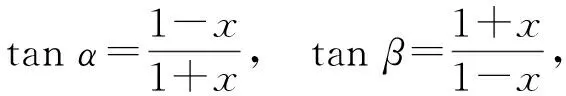
即

tanαtanβ=1.

因此点P的轨迹是以B,C为顶点的双曲线.

(此方法只有两个小组得出.)

方法4利用旋转变换证明.

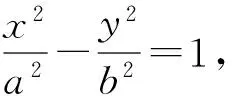
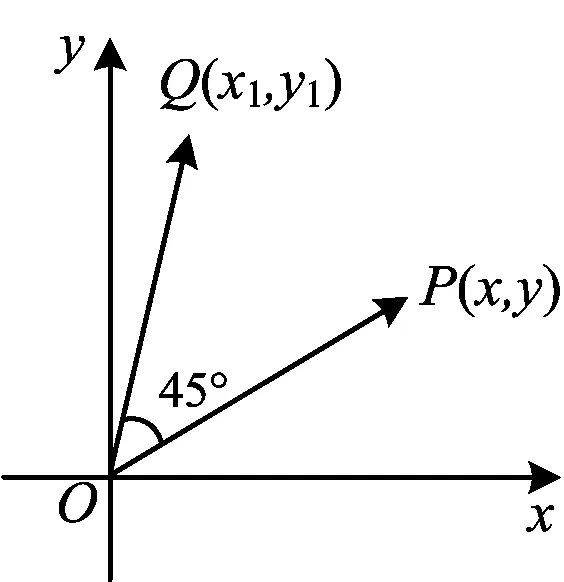
图6

先考虑一点绕原点按逆时针方向旋转45°后坐标的关系.如图6，设P(x,y)绕原点O逆时针旋转45°后得到点Q(x1,y1)，则∠POQ=45°.又设|OP|=r，∠xOP=α，则

|OQ|=r， ∠xOQ=α+45°，

从而

x=rcosα，y=rsinα；

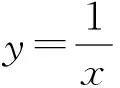
(此方法仅该小组得出.)

2 案例分析

2．1 “长作业”是一种探究性课程资源

新课程倡导探究性学习，学生应该是探究的主体，因此，整个课程编制过程要适合学生探究学习.此次“长作业”从布置作业那一天起到上探究成果汇报课，学生们根据教师布置的任务，进行了一系列的探究学习.由于问题的结论是存在的，这就激发了学生探究其过程奥秘的欲望.绝大部分学生都能利用双曲线定义探究证明了“反比例函数的图像是双曲线”这一论断，并在探究过程中享受了成功的愉悦；有的学生不满足于双曲线定义这一方法，还能从双曲线第二定义视角进行探究，也获得了成功；还有少数学生另辟蹊径，分别从轨迹问题和旋转变换视角，得到了另外两种方法.因此，“长作业”是一种探究性课程资源.

2．2 “长作业”是一种反思性课程资源

反思性课程资源是指能促进师生进行反思的课程资源，学生需要对自己的学习情况进行反思，教师需要对教学情况进行反思.反思性数学学习可以重构自己对问题的理解，产生超越已有信息外的信息.数学教师需针对学生的学情设计一些反思性问题让学生不断进行反思，从而深化拓展知识，提高学生的思维能力.

而在“长作业”的探究学习过程中，学生必须反思过去曾学习过的知识和方法，比如探究“为什么反比例函数的图像是双曲线”，若反思联想双曲线的定义，则可利用双曲线定义进行判断；若反思联想双曲线的第二定义，则可利用双曲线第二定义进行判断；若反思联想双曲线有关轨迹问题，则可利用双曲线轨迹题的结论进行判断；若反思联想旋转变换，就有可能将双曲线作旋转变换进行判断.因此，“长作业”是一种反思性课程资源.

2．3 “长作业”是一种拓展性课程资源

“拓展”是指“开拓扩展”.“长作业”也是一种具有拓展性质的课程资源.首先，“长作业”的内容可以是课本中的有关习题，也可以是课本问题的延伸、拓展.本案例的问题“为什么反比例函数的图像是双曲线”便是课本问题的延伸、拓展.由于“长作业”是布置给学生在课堂外的时间完成的，促使了学生把数学学习空间从课堂上拓展到了课堂外，学生需要自己查阅资料、自主探索或与同学交流，也就是说，“长作业”拓展了学生的数学学习方式.这样，学生的数学学习方式就更多了，如阅读自学、交流合作、动手探索等等，而不是只有机械的记忆和接受、简单的模仿与练习.因此，“长作业”也是一种具有拓展性质的课程资源，拓展了学生的数学学习方式.

3 “长作业”的设计

3.1 “长作业”的设计原则

选择一个恰当的具有教育价值的“长作业”是保障学生自主学习顺利进行的首要条件，笔者认为设计“长作业”可以参考以下原则：

1)形成性原则.“长作业”的设计要把重点放在方法与过程上，注重开放性和探究性，这样有利于形成知识与方法，提高能力.

2)多样性原则.“长作业”的形式可以多种多样，制作模型、实验探究、观察记录等都可以成为形式.“长作业”可以由教师提出设计，也可以鼓励学生自己提供；可以是全班学生做同一个题目，也可以让学生根据自己的兴趣爱好和特长，制定个性化的内容，以小组形式甚至是个人单独完成，充分发挥特长，挖掘潜能.

3)发展性原则.“长作业”的内容设计也要与时俱进，选择能提高学生的知识和技能、对学生后继学习有用的一些问题，或者是前沿知识的热点问题.

4)循序渐进原则.“长作业”的设计要符合学生现有的认知水平，尽量把题目设置在思维最近发展区,还可以根据学生的智力和个性发展的差异，布置适合不同层次学生的作业.

3．2 “长作业”的分类

根据以上“长作业”的设计原则.结合教材中的“阅读与思考”“探究与发现”等栏目的内容，“长作业”可以分类如下：

1)调查性作业即指学生可以参加调查，在调查的活动中逐渐收集、分析信息而获得知识的作业.

2)实践性作业即指学生通过实践活动(或称实验活动)而获得知识的作业.

3)拓展性作业即指根据学生实际需要，对教材里面的有关内容(如例题、习题)、或课堂上实时生成的问题进一步拓展与提高，受限于时间，可以把遇到的问题改成课外作业，要求学生在课外探究和解决.

3．3 “长作业”的评价

因为完成“长作业”的时间(过程)较长，不适宜单一地用“对”“错”来评价.事实上,如果只关注结果而忽视过程，那么“长作业”很难能收到预期的效果.因此，还需研究“长作业”如何进行有效评价，常用的评价方法有：

1)成果汇报展示，如上述案例的展示过程.

2)注重过程评价，要对主要环节进行评价，如实践活动(或实验活动)的计划以及实践过程中的相关记录等等.

3)运用多元评价，如：①分层评价，对于不同能力层次的学生，评价时要有不同的评价要求；②生生互评，如在学习立体几何时，可以要求学生制作一些立体模型，然后利用作品展示法，让学生评选出最佳作品，这样既可以促进学生之间的交流，也可以提高他们的观察和鉴赏能力；③师生互评，如对一些分小组合作完成的作业，可以评价小组成员的参与度与有效性，一方面应由小组成员相互评价，另一方面，教师还要对各个组员进行评价.

[1] 郑日锋.“长作业”引发探究性学习的一个案例[J].数学通报，2007(4)：15-17.