基于奇异值分解理论的钢轨断裂检测方法

赵 建，张友鹏，赵 斌

ZHAO Jian,ZHANG Youpeng,ZHAO Bin

兰州交通大学 自动化与电气工程学院，兰州 730070

School ofAutomation and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

1 引言

铁路钢轨是轨道交通运输系统中的重要组成部件。铁路运营线路上如果出现钢轨断裂就有可能造成列车脱轨、倾覆等重大行车事故[1-3]。因此，为了预防钢轨断裂事故的发生，前期的检测方法和检测系统的研发备受关注[4]。目前，我国主要采用钢轨探伤小车、大型钢轨探伤车定期在轨道上检查以及轨道电路进行断轨检测[5]。随着高速铁路的发展，探伤小车和大型钢轨探伤车对钢轨断裂的检测已经无法满足新形势下对检测速度和断轨检出率的要求[1]。从已公开的专利、文献来看，基于轨道电路原理的实时断轨检测方法得到了普遍重视[6]。而在我国普遍应用的ZPW-2000A轨道电路依靠断轨时接收器处的轨道继电器因信号电流消失而释放，使区间轨道电路显示“红光带”提示断轨，但轨道电路受本身道床参数情况影响大，在道床电阻较小时经常发生轨间短路和“红光带”误报等故障[5]，而使其轨检测功能受到影响。因此，改进钢轨断裂检测的方法是十分必要和迫切的工作。

本文依据轨道电路断裂态的特性，结合ZPW-2000A无绝缘轨道电路的结构特点，首先建立了基于均匀传输线理论的列车分路条件下轨道电路断裂态的四端网模型，并通过该模型求得分路电流幅值函数。然后对分路电流幅值包络进行多分辨奇异值分解，确定了幅值包络中的突变点，进而通过换算关系得到钢轨断裂点的准确位置。本文提出的检测方法验证了利用机车感应电压信号进行钢轨断裂检测的可行性，弥补了ZPW-2000A轨道电路在钢轨断裂检测方面的不足，从而为运营安全和效率提供保障。

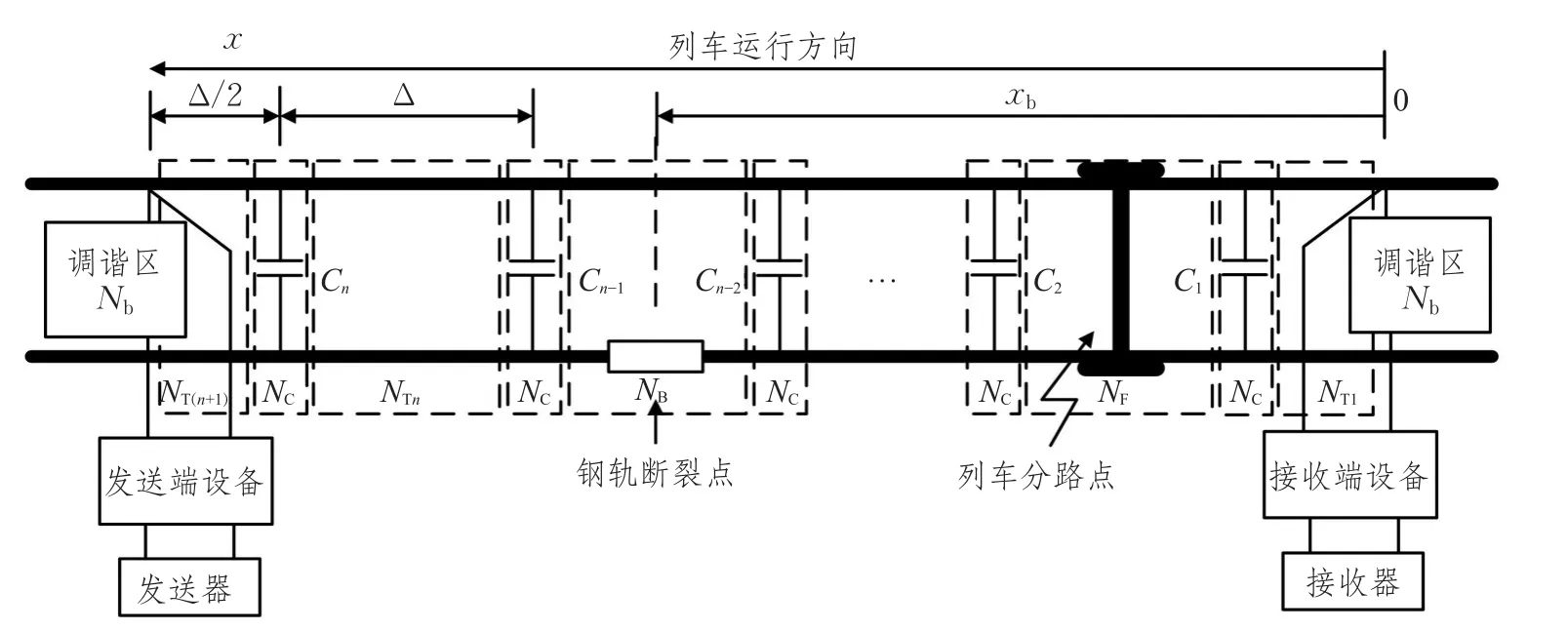
图1 钢轨断裂时列车分路结构示意图

2 钢轨断裂对机车分路电流的影响

钢轨发生断裂时，轨条并未完全断裂且仍存在电气连接，故可将钢轨断裂点等效为阻抗Zb，其值大小与钢轨特性阻抗ZB相关[7]，本文模型中设Zb与ZB间为线性映射。分析可知当Zb=0时，轨道电路工作在调整态；当Zb=∞时，轨道电路处于断轨态。而当Zb∈(0,∞)时，轨道电路工作在断裂态，即钢轨在距离接收端xb处出现裂纹。

理想情况下，可将轨道电路等效成均匀分布的传输线，用四端网络来描述其信号的传输特性[8]。如图1所示，主轨道被n个等值的补偿电容分为n+1段，且两补偿电容间的距离为Δ，轨道电路两端与补偿电容的距离为本文以接收端调谐区始端为坐标原点，列车分路点的坐标为x，将补偿电容分割的轨道区段分为调整状态单元NTi(i=1,2,…,n+1)、分路状态单元NF(x)和断裂状态单元NB。若分路点与断裂点在一个单元内，用四端网NBF(x)描述其传输特性。

由上述分析可得如图2所示的无绝缘轨道电路分路状态等效模型。Us(t)、Is(t)为发送端输出电压、电流，Uf(t,x)、If(t,x)为分路点前接收到的电压、电流，且有Uf(t,x)=If(t,x)×Rf，其中 Rf为分路电阻。 NFS为发送端设备传输四端网（发送端设备包括传输电缆和匹配变压器），Nb为发送端调谐区四端网，NT(x)为发送端调谐区末端到分路点之间主轨道的传输四端网。

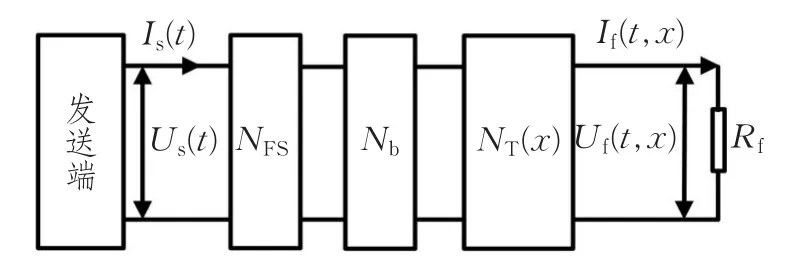
图2 无绝缘轨道电路分路状态等效模型

分路点到发送端调谐区末端之间的轨道四端网NT(x)可由式（1）表示。式中NF(x)为分路点x至分路点靠近发送端一侧的补偿电容Ck(k=1,2,…,n)间的轨道四端网。

列车进入断裂点单元时分路点x至Ck间的轨道四端网用NBF(x)表示，此时NT(x)如式（2）所示：

调整状态单元NTi和分路状态单元NF(x)四端网系数表达式可由均匀传输线理论求得。断裂状态单元NB和断裂且分路单元NBF(x)的四端网系数本文采用分布参数法求得。如式（3）所示为轨道电路的钢轨四端网系数的基本方程式[10]。、表示钢轨线路上任意点的对地电压（V）、、表示两根钢轨上流过的电流（A）；A1、A2、A3和 A4均为积分常数，其值为待定参数，由轨道电路的边界条件确定。

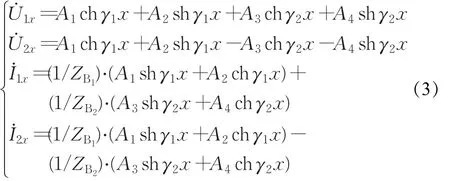
ZB1为对称钢轨线路的钢轨与大地间的特性阻抗，，E为大地常数，P为钢轨的表面电导系数；ZB2为对称钢轨的相线电路的特性阻抗，ZB2=ZB/2；ZB为对称钢轨线路的特性阻抗；γ1为钢轨线路的地线传播常数为钢轨线路的相线传播常数，γ2=γ；γ为钢轨线路传播常数。Zg为钢轨阻抗，Rd为道砟电阻，Zg和Rd称为轨道电路的一次参数[7，11]。

图3 断裂态单元等效电路

将钢轨断裂点设为坐标原点，断裂点到始端距离为l1（m），断裂点到终端距离为l2（m），整个断裂单元的长度为 l（m），即 l=l1+l2。 A1、A2、A3和 A4为断裂点与始端之间的轨道电路积分常数；B1、B2、B3和B4表示断裂点与终端之间的积分常数。若钢轨线路在距离接收端xb处的第m个单元内断裂，则有下式成立：

其中，[⋅]为取整函数，则l1=Δ⋅m-Δ/2-xb，l2=xb-Δ⋅m+3Δ/2。

积分常数 A1、A2、A3、A4、B1、B2、B3和 B4由以下边界条件确定[12]。

条件1当x=0时，有：

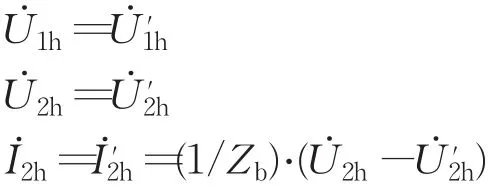
条件2当x=l1时，有：

条件3当x=-l2时，有：

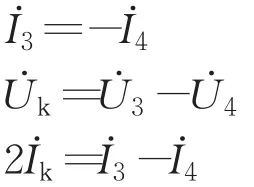
将式（3）代入这三个边界条件中，经计算化简得以下方程：

根据式（6）可求得 A1～A4和 B1～B4，且此时有下式成立：

将A3和A4代入式（7）化简可求得此轨道电路单元的轨道四端网系数A～D，即：

其中，n=ctγ1l2+ctγ1l1。

当列车分路点在钢轨断裂点所在单元，且未越过断裂点时的等效电路如图4所示。图中以断裂点和分路点为界将整个轨道电路单元分为三个部分，因本文只考虑分路点前电压、电流的变化情况，所以只需计算分路点之前的轨道四端网系数。

图4 分路且断裂状态单元四端网模型

设置A1～A4、B1～B4八个积分常数即可求解出分路点之前的轨道四端网系数，l1为该轨道电路单元始端到断裂点的距离（m），l2表示断裂点到分路点的距离（m），l表示分路点到该单元始端的距离（m）。此时可以计算得出l1=Δ⋅m-Δ/2-xb，l2=xb-x，l=l1+l2。经计算在此条件下轨道四端网NBF(x)的系数表达式与断裂单元NB的轨道四端网系数表达式相同，均为l1、l2和l的函数。因此将此状态下的三个变量代入NB的四端网系数表达式中即可求得NBF(x)的四端网系数。

当列车越过断裂点以后，此时接收到的分路电流和电压不再受断裂点等效阻抗的影响，此时，轨道电路进入正常分路状态。此时NBF(x)四端网的系数表达式与NF(x)的四端网系数表达式相同，在此不再赘述。

由以上分析求解出上述两种状态下轨道四端网NT(x)的系数表达式（3）或（4）。

则发送端到分路点间总的传输四端网F为：

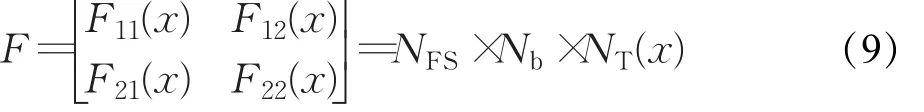
则由文献[13]可知，分路电流幅值函数| |If(t,x)可表示为：

根据ZPW-2000A无绝缘轨道电路的基本电气参数[9]，本文将仿真条件设置为：轨道电路长度1 600 m；补偿间距Δ为100 m；信号载频分路电阻 Rf=0.15 Ω；补偿电容16个，容值均为40 μF。与轨道电路有关的参数取值[7，10]：Zg=14.75∠82.3°Ω/km，Rd=1.0 Ω·km，E=1，P=9。

本文建立的模型中将钢轨断裂点等效成阻抗Zb，Zb的大小将会影响分路电流幅值包络曲线的变化情况。如图5所示是其他参数确定时，不同Zb取值下分路电流幅值包络曲线的仿真结果。

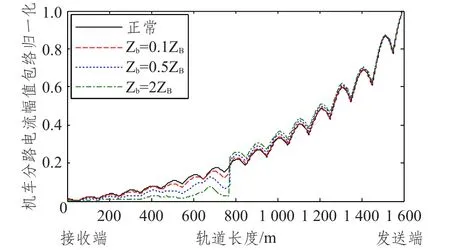
图5 不同断裂点等效阻抗值下仿真结果

由图5可知，在正常情况下，分路电流幅值包络在补偿电容的补偿作用下从接收端到发送端呈现“波浪”式递增，每个极小值点都和补偿电容的位置相对应，且在两补偿电容间的曲线并无突变点；两补偿电容间钢轨出现断裂后，对断裂点前的分路电流幅值包络曲线影响较大，主要表现为幅值下降且“波峰”和“波谷”变化不明显，这主要是因为钢轨的断裂影响了补偿电容的补偿效果；对断裂点之后的曲线影响较小，曲线的轮廓和正常状态相同但幅值略有增大，这是由断裂点后的电压突变引起的。同时等效阻抗Zb越大，断裂点前的分路电流幅值包络曲线衰减越大，而断裂点后的曲线会略有增大。因此Zb越大，断裂点前后的幅值包络曲线的变化越明显。

3 钢轨断裂故障检测方法

机车感应电压幅值包络Vg(t,x)与钢轨分路电流If(t,x)之间存在如下关系[13]：

其中，Bf为机车接受线圈的感应电压转换系数，当信号频率一定时，可近似认为是常数。在列车行驶过程中，Vg(t,x)的数据会被列车车载轨道电路读取器（Track Circuit Reader，TCR）所记录，将其作为钢轨断裂检测的数据来源不仅不需要增加其他辅助设备，也能兼顾检测数据及时有效，这将为钢轨维护和铁路运营管理提供新的依据。但目前在实际中，这一数据仅被用来诊断补偿电容故障，尚未被用来进行钢轨断裂检测。

如图5所示，对于Zb较大（如Zb=2ZB）时的分路电流幅值包络容易分辨出突变点的位置，而当Zb较小（如Zb=0.1ZB）时，钢轨的断裂对分路电流幅值包络的影响很小，是否发生突变以及突变点的位置情况很难辨识，因此必须采用信号处理的方法来判断分路电流幅值包络曲线是否发生突变，以及突变点的准确位置。在信号处理的过程中，信号的奇异值点可以反映由故障引起的撞击、震荡，及结构的变形和断裂[14]，因此找出钢轨断裂后分路电流幅值包络的奇异值点，通过奇异值点和钢轨断裂点的对应位置关系确定钢轨断裂点的位置。通过对比，选择不会使检测结果发生偏移的MRSVD分解方法进行信号奇异性的检测[15]，利用分解后细节信号的零交叉点判断出信号奇异值点的位置，即是钢轨断裂点的位置。

由于信号的奇异性检测会受到噪声信号的干扰[15]，因此需要注意的是在实际检测过程中，需要选择合适的信号降噪方法，对输入的机车感应电压信号进行降噪处理，减小噪声对断裂点位置判断的影响，使其达到最佳的检测效果。

4 MRSVD方法

奇异值分解（Singular Value Decomposition，SVD）是对于任意实数矩阵通过对其左、右分别乘一个正交矩阵，将原矩阵转化为一个对角阵的一种正交变换，此过程中得到的奇异值个数能反映原矩阵中独立行（列）矢量的个数[15-16]。多分辨奇异值分解（Multi-Resolution Singular Value Decomposition，MRSVD）是借鉴小波分析的思想利用SVD方法获得信号在不同层次空间、具有不同分辨率的结果从而实现类似于小波分析那样的可将信号分解到一系列不同层次子空间的多分辨率分解方法[14]，可准确判别信号的奇异值点，因此本文可以采用此方法进行钢轨断裂检测。

4.1 MRSVD算法的基本理论

SVD的定义为：对于一个矩阵H∈Rm×n，无论行列是否相关，必定存在正交矩阵U=(u1,u2,…,um)∈Rm×m和正交矩阵V=(v1,v2,…,vm)∈Rm×m使得式（12）成立：

利用SVD进行信号处理时，首先必须构造出Hankel矩阵H。设有离散数字信号x=(x1,x2,…,xN)，利用此矩阵构造的Hankel矩阵如下：

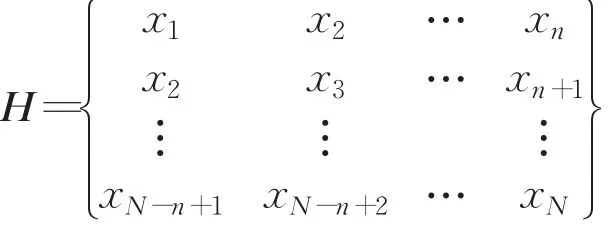
式中，1＜n＜N 。令m=N-n+1，则 H∈Rm×n。

MRSVD是对离散信号构造行数为2的Hankel矩阵，即：

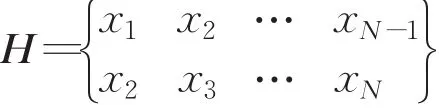
矩阵H经过SVD处理后得到两个奇异值σaj和σdj，且σaj＞σdj。从这两个奇异值分别可以得到两个信号分量信号Aj和 Dj，Aj称为SVD近似信号，它反映了原始信号的主要成分，Dj称为SVD细节信号，它反映了此次分解从原信号中获取的细枝末节。然后利用Aj信号继续构造行数为2的H矩阵进行下一层SVD分解。如此反复，就可将原信号分解为一系列SVD近似信号和细节信号，分解过程如图6所示。

图6 信号MRSVD分解过程

4.2 MRSVD分解算法

设分解 j-1次后得到 j-1次SVD近似信号Aj-1，记为Aj-1=(aj-1,1,aj-1,2,…,aj-1,N)，式中N为信号长度，构造Hankel矩阵 Hj为：

对Hj进行SVD分解得到：

式中Uj=(uj1,uj2)，Uj∈R2×2称为第 j次的左正交矩阵，称为第 j次的右正交矩阵。而式中的σaj和σdj称为第 j次获得的近似和细节信号奇异值。

将式（13）改写为列矢量Uji、Vji的表示形式如式（14）所示：

设Aj和Dj分别为第 j次近似信号和细节信号，它们由Haj和Hdj重构而成。以Aj为例，如图7所示，Haj的两个行矢量为σajUj1,1Vj1T和σajUj1,2Vj1T，其中Uj1,1、Uj1,2为Uj1的两个坐标。设La1和La2是这两个行矢量的子矢量，La1和 La2均代表 Aj的数据aj,2,aj,3,…,aj,N-1，但 La1和 La2并不相等。例如aj,2在 La1中为σajUj1,1Vj1,2，而 La2中 aj,2的值为 σajUj1,2Vj1,1。将 Haj中代表Aj中同一数据的所有元素求平均作为Aj中的相应数据，可将Aj写成如下矢量形式：

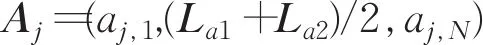
图7 近似矩阵Haj中的矢量

用同样的方法可构造出细节信号Dj，Aj和Dj便是第 j次的分解结果。再利用Aj构造出Hankel矩阵Hj+1，进行同样的处理，如此反复就可得到一系列的SVD近似和细节信号。

5 仿真分析

如图8所示，当Zb=0.1ZB时的分路电流幅值包络曲线与正常时近似重合，此时很难准确判断是否发生钢轨断裂以及断裂点的位置，需要采用信号处理的方法进行判断。

经多次实验，本文取三次MRSVD分解后的细节信号能够表征分路电流信号的全部特征。图9为正常情况下三次MRSVD的分解的细节信号结果，如图中所示，在正常状态下经过MRSVD分解的分路电流幅值包络曲线的细节信号出现了16个向下的峰值点，它们分别对应幅值包络曲线中的16个极小值点，同时也对应着轨道线路中的16个补偿电容的位置。而从分解效果上来看，第三次分解的效果最为理想。图10为Zb=0.1ZB时对分路电流幅值包络曲线经过三次MRSVD分解后的细节信号图像，图中除了和补偿电容位置相对应的16个峰值点外，还出现了一个奇异值点，经计算得出奇异值点的位置对应钢轨的断裂点坐标。而从分解的细节信号来看，第三次分解时的细节信号能完整反映出原信号的全部细节特征，包括全部的补偿电容位置和钢轨断裂点的位置。

图8 Zb=0.1ZB分路电流幅值包络曲线

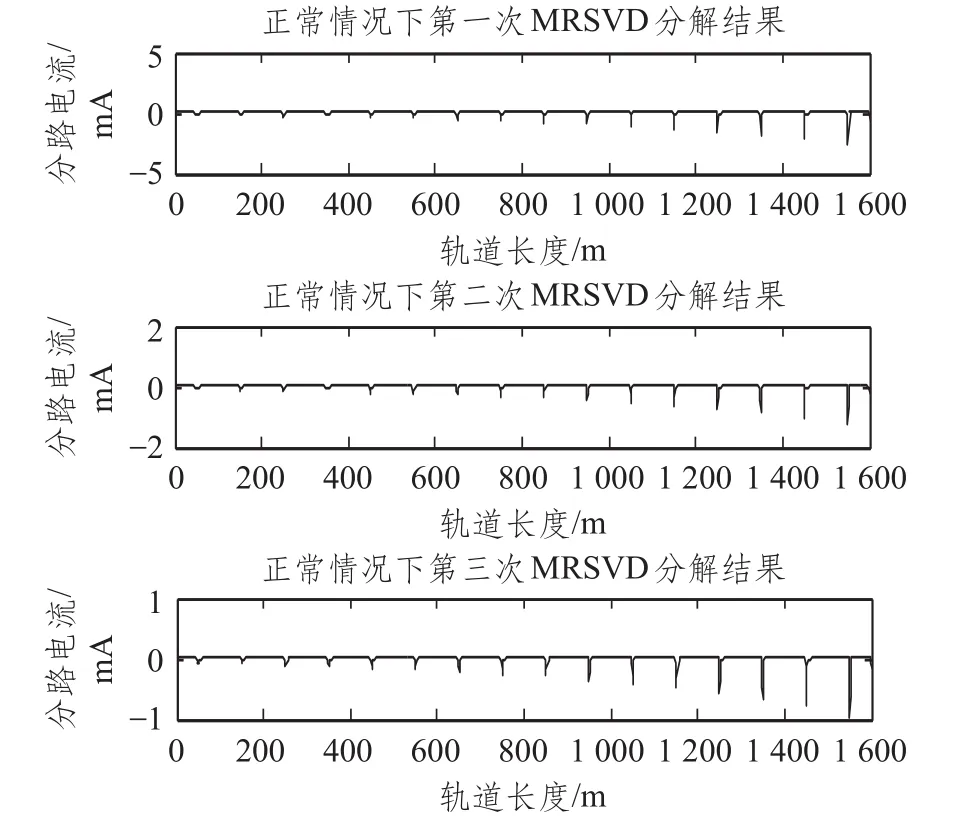
图9 正常情况下三次MRSVD细节信号

图10 Zb=0.1ZB时三次MRSVD细节信号

为了验证MRSVD分解方法的有效性，将断裂点等效阻抗取为Zb=0.01ZB进行试验。如图11（a）所示是Zb=0.01ZB的分路电流幅值包络曲线，从图中可以看出，此时两条曲线已经完全重合，无法分辨出是否发生了钢轨断裂，更无法判断断裂点的准确位置。图（b）为Zb=0.01ZB的三次MRSVD分解后的细节信号图像，图中16个峰值点的位置对应补偿电容的位置，且经换算图中的奇异值点的位置对应钢轨断裂点的位置。因此利用MRSVD方法分解分路电流幅值包络曲线，利用分解后的细节信号的奇异性特征，可以判断钢轨线路是否发生了断裂，而利用奇异值点坐标可以对钢轨上的断裂点准确定位。

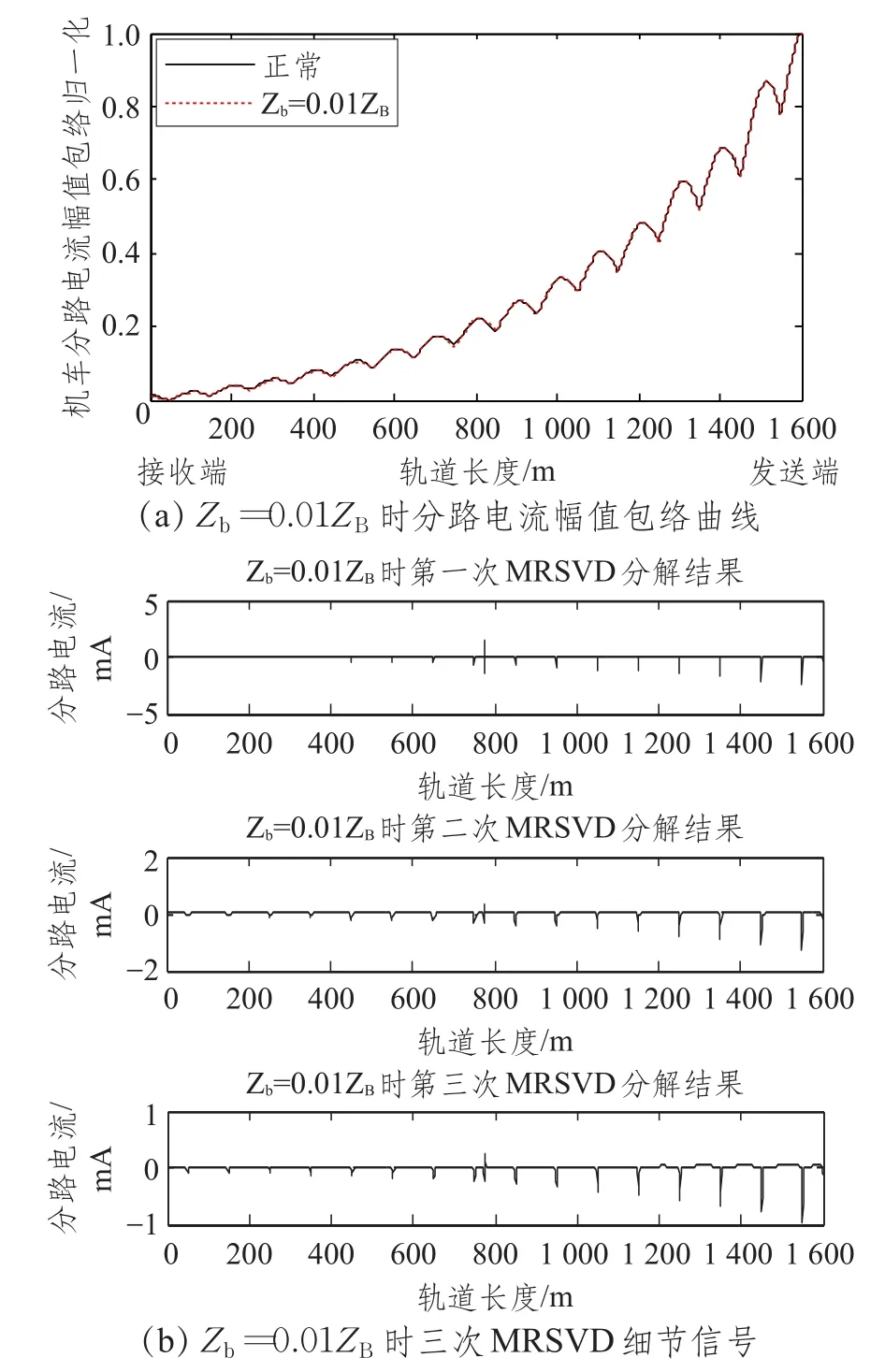
图11 Zb=0.01ZB时的仿真结果

图12 C8断线和C8处钢轨断裂时的仿真结果

另外，补偿电容的断线故障同样也会影响分路电流幅值包络曲线的形状。通过实验，本文方法可以有效区分补偿电容断线和补偿电容处钢轨断裂这两种不同类型的故障。如图12（a）所示是补偿电容C8断线和C8（750 m）处钢轨断裂的分路电流幅值包络曲线图，这两种故障都主要影响接收端到C8处的分路电流幅值包络曲线。但C8断线后补偿效果消失，使包络曲线一直递增至C8处；C8处钢轨断裂后，包络曲线先增后减，到C8处时直接“跳跃”至与正常值范围内。图12（b）和图12（c）是这两种故障曲线进行MRSVD分解后的细节信号曲线，由图12（a）可知，C8断线后的三次MRSVD分解后的细节信号在C8处峰值点均消失了，说明C8的补偿效果消失了。图12（c）中，在C8处出现了奇异值点，根据上文的分析

为了验证本文模型的正确性，将本文断裂态单元分别替换成文献[7]中轨道电路分路态与断轨态四端网系数，建立仿真模型进行对比试验。将本文模型取Zb=0、Zb=∞与文献[7]中正常状态和断轨状态为基础建立的模型进行仿真对比，仿真结果如图13所示。由图13可知，本文模型在Zb=0时和以文献[7]中正常状态为基础建立模型的仿真结果相同，Zb=∞时与以文献[7]中断轨状态为基础建立的模型的仿真结果相同。同时，当轨道电路处于正常状态时，即Zb=0时，分路电流幅值包络将不受影响；而当轨道电路处于断轨状态时，即Zb=∞时，发送电流仍可通过地与两条钢轨构成回路，此时仍能接收到微弱的电流信号[7]。由此，可以验证本文模型的正确性。

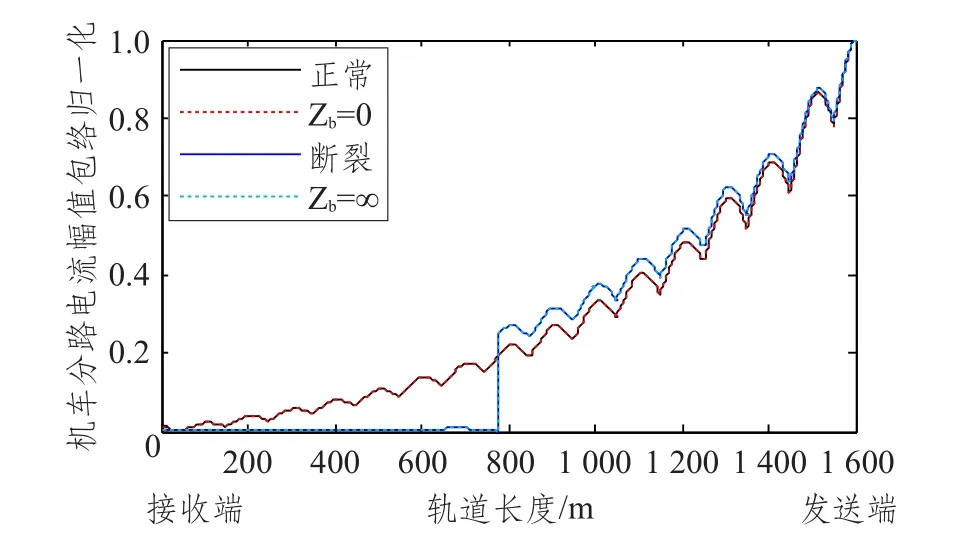
图13 Zb=0和Zb=∞时的仿真结果

6 结束语

本文利用多分辨奇异值分解法对钢轨断裂后的短路电流幅值包络曲线进行分解，根据分解后细节信号的奇异值点与钢轨断裂点的对应位置关系实现对钢轨断裂的检测，仿真分析表明：

（1）钢轨断裂将主要影响断裂点之前的分路电流幅值包络曲线，同时等效阻抗Zb越大，断裂点前的曲线衰减越大，但无论Zb如何变化，曲线在断裂点位置处总存在突变点。

（2）利用多分辨奇异值分解法对钢轨断裂后的分路电流幅值包络曲线进行分解，根据分解后细节信号的奇异值点与钢轨断裂点的对应位置关系实现对钢轨断裂的检测。该方法能够准确检测出钢轨是否发生了断裂，以及钢轨断裂点的具体位置。同时可以有效地区分补偿电容断线和补偿电容处钢轨断裂这两种不同的故障。

（3）本文所采用方法的实际数据可以从机车记录数据中获得，使该方法具有成本低、实时性好和检测断裂点位置准确等优点。

参考文献：

[1]李浩，段翔宇，白彪.基于超声导波的无缝线路断轨检测系统[J].电子设计工程，2015，23（16）：126-129.

[2]Domingo L M，Giner B B，Martin C Z，et al.Experimental modal analysis of transverse-cracked rails-influence of the cracks on the real track behavior[J].Structural Engineering and Mechanics，2014，52（5）：1019-1032.

[3]Veskovic S，Tepic J，Ivic M，et al.Model for predicting the frequency of broken rails[J].Metalurgija，2012，51（2）：221-224.

[4]Kostryzhev A G，Davis C L，Roberts C.Detection of crack growth in rail steel using acoustic emission[J].Ironmaking and Steelmaking，2013，40（2）：98-102.

[5]史宏章，任远，张友鹏，等.国内外断轨检测技术发展的现状与研究[J].铁道运营技术，2010，16（4）：1-3.

[6]田铭兴，赵斌，闵永智.基于轨道电路原理的新型实时断轨检测方法[J].兰州交通大学学报，2013，32（1）：58-62.

[7]阿·米·布列也夫.轨道电路分析与综合[M].孙名甫，译.北京：中国铁道出版社，1981：90-100.

[8]赵会兵，章宇舟，汪希时.电容补偿式轨道电路若干问题的研究[J].铁道学报，1998，20（4）：1-5.

[9]董昱.区间信号与列车运行控制系统[M].北京：中国铁道出版社，2008：90-125.

[10]张友鹏，刘鹍鹏，赵斌，等.ZPW-2000A轨道电路断轨态分析[J].控制工程，2014，21（5）：695-699.

[11]刘鹍鹏，张友鹏，赵斌，等.实时断轨检测技术发送系统设计[J].铁道科学与工程学报，2013，10（1）：123-128.

[12]赵斌.基于轨道电路行波的钢轨断裂检测理论与仿真[D].兰州：兰州交通大学，2016.

[13]赵林海，蔡伯根，邱宽民，等.基于HHT_DBWT的无绝缘轨道电路补偿电容故障诊断[J].铁道学报，2011，3（33）：49-54.

[14]赵学智，叶邦彦，陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用[J].机械工程学报，2010，46（20）：64-75.

[15]Hernández A，Espinosa-Juárez E，de Castro R M，et al.SVD applied to voltage sag state estimation[J].IEEE Transactions on Power Delivery，2013，28（2）：866-873.

[16]McGivney D F，Pierre E，Ma D，et al.SVD Compression for magnetic resonance fingerprinting in the time domain[J].IEEE Transactions on Medical Imaging，2014，33（12）：2311-2322.

[17]郑安总.奇异值分解在微弱信号检测中的应用[D].天津：天津大学，2013.