一类特殊的非抢占式周期任务的调度方法

李智翔，李 赟，贺 亮

LI Zhixiang,LI Yun,HE Liang

盲信号处理重点实验室，成都 610041

National Key Laboratory of Science and Technology on Blind Signal Processing,Chengdu 610041,China

1 引言

对单处理器实时系统而言，通常存在多个不同的任务，同一时刻只能对一个任务进行处理；不同的任务有不同的开始时间、执行时间、截止时间等等约束因素；当存在多个任务时，如何通过合理安排不同任务的执行时间，使得单处理器实时系统能够对这些任务进行处理，这就是调度方法需要解决的问题[1]。

周期任务调度问题是当前研究的热点问题之一[2-4]。Liu和Layland提出了一种通用的周期任务模型[5]，该模型假设任务之间相互独立，并根据不同的调度情况，可以将调度问题分成静态调度问题和动态调度问题。RM（Rate Monotonic）算法[6]和 EDF（Earliest Deadline First）算法[7]分别是这两类调度算法中的典型代表。其中，EDF算法总是优先选择截止期最早的任务进行调度，而RM算法则根据任务的周期进行优先级调度，周期越小，优先级越高。

当任务开始执行后，如出现其他优先级更高的任务，按照是否可以替换当前正在执行任务，将调度问题划分成可抢占式（preemptive）调度问题和非抢占式（non-preemptive）调度问题。对可抢占式调度问题，学界已有较为充分的研究和理论成果[8]。在实际系统中，由于硬件条件的限制以及效率和性能的考虑，存在非常多的系统并不支持可抢占式调度，如控制器局域网络（Control Area Network，CAN）的总线消息传递问题[9]。与可抢占式调度问题不同，非抢占式调度问题已经被证明是NP难问题[10]，可抢占式调度问题中得到的可调度条件在非抢占式调度问题中最多也仅为必要条件[11]。学者针对不同实际场景的特点，提出了解决相应非抢占式调度问题的一系列优秀算法[12-14]。

对通常研究的周期性调度问题而言，如控制系统中的采样、计算、输出等周期性任务，需要在给定的任务执行周期中分配一定时长的处理资源，这里的任务执行周期是固定不变的，每次任务执行时间只要包含在任务执行周期中即可，特定任务的相邻两次执行之间不存在关联和约束，如图1（a）所示。在现实世界中存在这样的一类特殊的周期任务调度问题，如监视类问题、资源补给类问题、温度控制类问题等，其调度的资源在使用上具有一定的时效性，故要求特定任务相邻两次执行的时间间隔不得大于某给定值，否则必然存在一段时间该任务未被分配资源，如图1（b）所示，本文关注此类调度问题。举例说明，对某监视类调度任务而言，对某特定目标需要至少每10 s执行一次2 s的扫描操作，以保证对可能出现的异常情况进行及时处理。在实际调度时必须保证任意连续两次扫描之间的时间间隔不大于10 s，若采用通常的非抢占式周期任务调度模型和算法，只约束每10 s有2 s的扫描，则前后两次扫描之间的时间间隔可能大于10 s（如图1（a）中第1、2周期任务执行之间的间隔大于周期长度），这样的调度结果不符合这里监视任务的实际要求。也就是说，通常的非抢占式周期任务调度模型和相应算法在此类资源使用具有时效性的调度问题上不适用，需要为此类问题研究新的调度模型和相应算法。

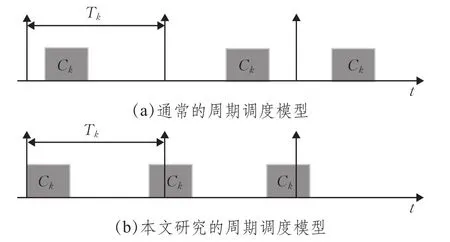
图1 调度模型

2 特殊的非抢占式周期任务调度问题

在本文涉及的非抢占式周期调度问题中，对任意任务oi，记任务执行时间为Ci，任务执行周期为Ti，其关系如图1（b）所示。对可行的调度方案作以下规定：

（1）特定时刻最多只能调度一个任务；

（2）允许处理器空闲；

（3）任意任务的任意一次执行时间严格等于Ci；

（4）对任意任务，其任意连续两次执行开始时刻之间的间隔不大于Ti。

本文研究单处理器可调度问题，对单处理器可调度问题定义如下：

定义1（单处理器可调度问题）给定n个任务{o1,o2,…,on}及相应参数 {Ci,Ti}∀i∈{0,1,…,n}，找出对这n个任务的单处理器可行调度方案。所有任务最小的重复周期称为调度周期，记作R。

本文关注的是此类特殊调度问题的可行解。举例说明，假设需要对4个任务进行调度，其参数{Ci,Ti}分别为{1，3}，{1，4}，{1，5}，{1，9}，单位：s。如图2所示，为可行调度方案的一个调度周期。从图中可以看出，每个任务均满足调度参数的要求，图2给出的调度方案是可行调度方案。

图2 调度问题示例

下面对本文研究的调度问题的计算复杂度进行证明。

定理1（NP完全性定理）本文研究的单处理器可调度问题为NP完全问题。

证明 首先证明问题为NP问题。任意给定一种调度方案，显然可以在多项式时间内判断该调度方案是否可行。故该问题为NP问题。

其次，需要将一个已知的NP完全问题在多项式时间内规约到该问题上。这里参考文献[15]对3-PARTITION问题的规约。3-PARTITON问题已经被证明是NP完全问题[16]。

首先对3-PARTITON问题进行说明：一个3-PARTITION问题包含3m个元素，这些元素构成一个有限集合A；给定一个常数B∈Z+，对集合A中的任意元素a∈A，有 B/4＜a＜B/2，且。问题即判断集合A是否能够划分成m个两两交集为空的子集S1,S2,…,Sm，且满足对根据上述定义，显然每个子集中应包含3个元素，故该问题被称为3-PARTITON问题。

下面进行规约。首先构造一个单处理器可调度问题，该问题包含任务集合{o1,o2,…,o3m,o3m+1}，参数{Ci,Ti}如下：

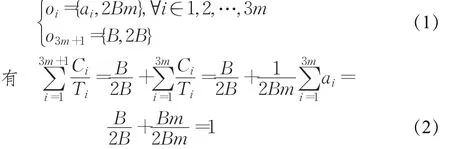
即若该问题存在可行调度方案，则该方案刚好将单处理器资源分配完，没有处理器空闲。首先对任务o3m+1进行调度分配，易知最优方案为每2B时长中包含一个长度为B的空闲时间片段，如图3所示。

进一步考虑对任务{o1,o2,…,o3m}进行调度规划。此时应有通道周期R=2Bm。从图3中可以看出，当前空闲时间片段为[2B(k-1),2Bk]，对∀k=1,2,…,m。这m个时间片段是互不相交的，并且每个时间片段的长度为B。若存在能够对任务{o1,o2,…,o3m,o3m+1}可行的调度方案，那么任务{o1,o2,…,o3m}一定能够分配到上述m个互不相交的时间片段中。又已知对集合A中的任意元素a∈A，有 B/4＜a＜B/2，由式（2），所以此可行调度方案一定是为上述m个互不相交的时间片段中的每个时间片段均分配3个任务，且对每个时间片段分配的任务有∑Ci/Ti=B，即∑ai=B，从而实际上将{o1,o2,…,o3m}对应的{C1,C2,…,C3m}进行了3-PARTITON问题中的划分。也就是说，本文的调度问题的解也是3-PARTITON问题的解。故该问题是NP完全问题。证毕。

图3 对特殊任务的最优分配

由于本文研究调度问题的计算复杂度较高，为NP完全问题，后续章节将从两个角度对该问题的求解算法进行分析：一方面采用剪枝的思想，尽可能降低搜索的复杂度，在此基础上提出一种模式剪枝算法；另一方面研究问题可调度的充分条件和必要条件，给出一种快速求解算法。

3 模式剪枝算法

考虑对本文研究调度问题进行暴力搜索的情形。假设n个任务的执行时间的最大公约数为1，设为基本时间单位。若允许处理器空闲，每个基本时间单位需要对n+1种可能性进行搜索，假设需要搜索的基本时间单位个数为m，那么在最差情况下的搜索复杂度为(n+1)m，为m的指数级，效率是无法接受的。若需要对可调度问题进行准确判别，则必须对搜索过程进行剪枝。

定义2（模式）给定任务{o1,o2,…,on}和调度参数{Ci,Ti}∀i∈{0,1,…,n}，模式是指任务执行时间 Ci的序列，任务执行时间称作模式的元素。一个正确的模式必须满足以下条件：

（2）模式中Ck仅在起始位置出现一次；

（3）模式的长度不能超过Tk。

将模式的起始元素限制为任务执行周期最大的任务的执行时间，是为了使不同模式的数量尽可能的大，模式的长度尽可能长，减少无效搜索的数量。

在定义模式的基础上，还需要对搜索过程进行剪枝。首先从以下两个方面考虑对模式进行剪枝：

（1）不满足任意元素对应任务的执行周期约束；

（2）调度冗余。

其中，调度冗余是指若模式中存在三个相同元素，且第一个和第三个元素之间的时间间隔满足对应任务的执行周期约束，那么第二个元素是冗余的，该模式是无意义的，应当剪枝。

通过对模式剪枝减少了不同模式的数量，通过对模式之间的连接可行性进行判别，可以进一步减少搜索范围。对任意模式维护一个可行的后续模式集合，对不可行的后续模式，按照以下条件进行剪枝：

（1）两个模式组成的序列中，不满足任意元素对应任务的执行周期约束；

（2）调度冗余。

通过上述条件的剪枝，进一步对模式的可行后续模式集合大小进行缩减，使得搜索空间进一步缩小。由此，本文给出了合法的模式集合以及每个模式的可行后续模式集合。下面给出模式剪枝算法的基本步骤：

步骤1生成所有可行模式。

步骤2生成所有可行模式的可行后续模式集合。

步骤3根据模式及其可行后续模式按照深度优先的方式依次遍历，直到出现已遍历的模式，分情况判断。

步骤3.1若该模式与第一个模式相同，则找到可行调度方案，输出从该模式之前的序列，作为一个调度周期，算法结束；

步骤3.2若该模式与其他模式相同，则进行剪枝，继续其他搜索。

模式剪枝算法给出了一种对本文调度问题精确求解的方法。当任务集合足够复杂时，尤其是对一些需要快速反应且可以接受次优解的实际应用场景，需要更快的算法进行计算。下一章将给出近似解的快速求解算法。

4 快速求解算法

首先给出一个可行调度的充分条件。

定理2（充分条件）给定一组任务{o1,o2,…,on}及其调度参数{Ci,Ti}∀i∈{0,1,…,n}，另一组任务及其调度参数。若对，有：

下面给出快速求解算法的基本流程。

步骤1按照式（4）对任务{o1,o2,…,on}的调度参数进行变化，得到新任务集合及其调度参数。

步骤3取调度周期为TK，将调度周期划分成K个相等的基本单元，并维护一个大小为K的数组V，其中V(i)=K,∀i=1,2,…,n，表示各单元可分配时间长度。

步骤4将任务ok分配到K个单元的开始位置，令V(i)=K-Ck,∀i=1,2,…,n。

步骤5将其他n-1个任务按照其变化后的攻击参数依次填入，根据数组V的值对能否填入进行判断；若某任务无法填入，则判定不可调度，算法结束；若可以填入，则依次填入并更新数组V的值，再对下一个任务进行资源分配。

步骤6若所有任务均已填入，输出结果，算法结束。

5 实验

5.1 实验设置

本节对本文提出的模式剪枝算法、快速求解算法以及基本的暴力搜索法进行对比测试，选用仿真测试函数和实际应用场景对算法进行评测。测试用计算机处理器为Intel®Xeon®CPU E5-2667 v3@3.2 GHz，内存为4 GB，操作系统为Windows 7专业版。相关仿真测试用例见表1所示。将三种算法的最大搜索时间设置为1 000 s，超过最大搜索时间视为算法无法对问题求解。

表1 测试用例属性

在选用测试用例对算法进行对比测试的基础上，本文还将在一种实际应用场景——网站监控问题上对本文算法进行对比测试。网站监控问题，是一种通过对不同网站合理分配监控资源，以实现对大量网站上传播的黄色、暴力等信息进行监测和控制的问题。在网站监控问题中，为了使特定网站的信息传播热度和范围可控，需要每隔不大于一定的时间对网站高热度内容进行一次扫描，即可实现全时段监控。本文提出的调度模型和相应算法适用于此类网站监控问题。假设当前只有一个监控主机，需要监控的网站数量为50个，特定时间只能对特定的一个网站进行监控；按照网站浏览量的不同，监控网站两次之间的最大时间间隔不同；按照网站大小的不同，每次监控分别需要的时间不同。相应参数取值范围如表2所示，其中监控最大时间间隔范围为1～3 h，最小单位为0.1 h，对应于本文研究调度问题中的任务执行周期；单次监控用时范围为0.5～2 min，最小单位为0.1 min，对应于本文研究调度问题中的任务执行时间；网站对应于调度的任务，其参数依照表2随机生成。本文共生成20组网站监控问题，对三种不同算法进行对比测试。

表2 网站舆论监控问题参数取值范围

5.2 实验结果和分析

图4为模式剪枝算法和快速求解算法得到的调度结果。可以看出，模式剪枝算法得到结果的调度周期长度为14，其中包含2个长度为1的空闲时间片段；快速求解算法得到结果的调度周期长度为3，无空闲时间片段。快速求解算法得到结果的调度周期长度较短，形式简单，但对处理器资源造成了一定的浪费，若需要进一步对如调度参数为{1，10}的任务进行调度，模式剪枝算法得到结果的剩余资源还能够继续分配给该任务，而快速求解算法就必须另外分配处理器了。结合表3中的算法用时，可以看出两种算法均比暴力搜索法效率高，而快速求解算法又比模式剪枝算法快3个数量级。

图4 测试用例1调度结果

表3 测试用例1算法用时对比

测试用例2中的任务执行时间、任务执行周期参数均为小数。图5为模式剪枝算法和快速求解算法得到的任务调度结果。可以看出，模式剪枝算法得到结果的调度周期长度为8.2，其中包含1个长度为0.7的空闲时间片段；快速求解算法得到结果的调度周期长度为2.8，无空闲时间片段。快速求解算法得到结果的调度周期长度较短，形式简单，但对资源造成了一定的浪费，若需要进一步对如调度参数为{0.7，8.2，0}的任务分配资源，模式剪枝算法得到结果剩余的处理器资源还能够继续分配给该任务，而快速求解算法就必须另外分配处理器了。结合表4中的算法用时，可以看出三种算法的用时对比与测试用例1类似，具体的，由于调度问题与测试用例1相比变得更加复杂（任务执行时间、任务执行周期参数均为小数），暴力搜索法的用时提升幅度较大；模式剪枝法的用时也有提升，但提升幅度小于暴力搜索法；而快速求解法则区别不大。这是因为对暴力搜索法和模式剪枝算法来讲，测试用例2搜索的基本时长单元为0.1，增大了搜索复杂度，故暴力搜索法的用时显著增大；而模式剪枝法采用模式的形式对搜索范围进行了有效地剪枝，其用时增大程度低于暴力搜索法；快速求解法用时不受参数影响，基本保持一致。

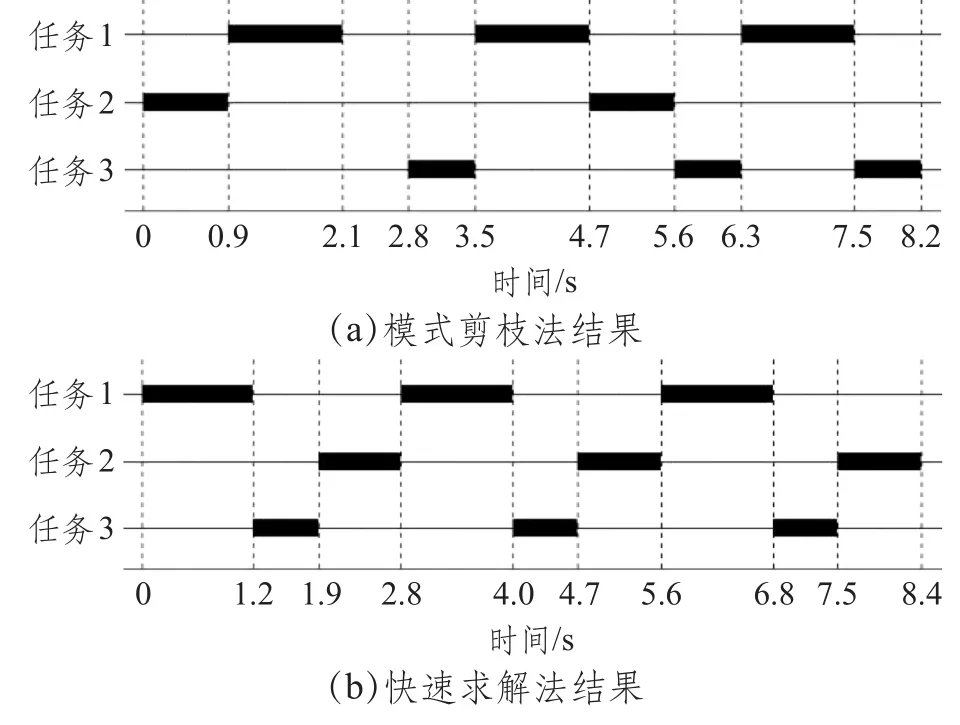
图5 测试用例2调度结果

表4 测试用例2算法用时对比

图6为模式剪枝算法得到的调度结果，而快速求解算法在该测试用例上无法得到可行调度结果。可以看出，模式剪枝算法得到结果的调度周期长度为12。结合表5中的算法用时，可以看出暴力搜索法已经无法在可接受的时间里对当前问题进行计算，模式剪枝算法用时与之前两个测试用例差别不大，而快速求解法无法得到可行调度结果。

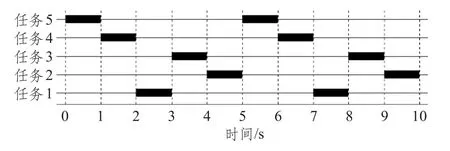
图6 测试用例3调度结果

表5 测试用例3算法用时对比

图7为快速求解算法得到的调度结果，而模式剪枝算法无法在可接受的时间里对当前问题进行有效计算。可以看出，快速求解算法得到结果的通道周期长度为8，无空闲时间片段。结合表6中的算法用时，可以看出暴力搜索法和模式剪枝算法已无法胜任此类复杂度的问题，而快速求解法的用时仍与之前三个测试用例基本一致。

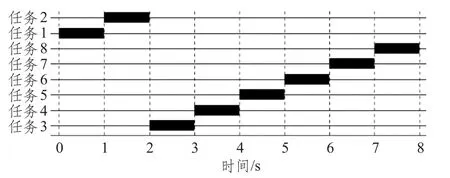
图7 测试用例4调度结果

表6 测试用例4算法用时对比

对网站监控的实际问题，本文依照表2中的参数范围随机生成了20组问题，并应用不同算法进行求解。由于任务数量过多，调度结果图过于冗杂，这里直接给出实验统计结果如表7所示。在20组问题中，暴力求解法和模式剪枝算法均没有成功求解，而快速求解算法成功求解了20组问题中的19组；从调度周期长度可以看出，快速求解法的调度周期长度为3 h，调度方案较为简单；从平均用时可以看出，由于该问题的复杂性较上述测试用例有了明显提升，快速求解算法的用时较上述测试用例提升了大约一个数量级，这是因为在调度周期长度基本保持不变的前提下，需要调度的任务数量提升了大约一个数量级。对于此类实际的复杂任务调度问题，只有快速求解算法能够在短时间内得到形式简单的调度方案。

表7 网站舆论监视问题算法对比

综上可以看出，针对本文研究的调度问题，模式剪枝算法和快速求解算法的算法执行效率均较暴力搜索法有了若干数量级的提升，而快速求解法的用时远优于其他两种方法，并且对不同问题的求解时间基本保持稳定。对于一些任务占用处理器资源较多的情况，此时快速求解法由于对问题进行了简化，可能无法得到解，而此时模式剪枝算法可以确保对最优解的求解。当任务数量较多，或空闲时间较多时，模式剪枝算法无法在可接受时间里求得解。故对于离线有充分时间求解的情况，可以选择模式剪枝算法；对于实时需要快速反应的情况，可以选择快速求解算法。

6 结束语

本文针对一种具有时效性的特殊的非抢占式周期任务调度问题开展研究，证明了该问题为NP完全问题，并根据不同的使用场景提出了模式剪枝和快速求解两种算法，分别适用于在时间充裕条件下精确求解的情况以及对时间效率要求较高时快速近似求解的情况。相关实验表明了本文提出算法的有效性。在未来，笔者将对模式剪枝法进行深入分析，尝试进一步提升算法的效率。

参考文献：

[1]Audsley N C，Burns A，Richardson M F，et al.Hard realtime scheduling：The deadline-monotonic approach[J].Ifac Proceedings Volumes，1991，24（2）：127-132.

[2]Ripoll I，Ballester-Ripoll R.Period selection for minimal hyperperiod in periodic task systems[J].IEEE Transactions on Computers，2013，62（9）：1813-1822.

[3]Nasri M，Fohler G.An efficient method for assigning harmonic periods to hard real-time tasks with period Ranges[C]//27th Euromicro Conference on Real-Time Systems，2015：149-159.

[4]Nasri M，Fohler G，Kargahi M.A framework to construct customized harmonic periods for real-time systems[C]//26th Euromicro Conference on Real-Time Systems，2014：211-220.

[5]Liu C L，Layland J W.Scheduling algorithms for multiprogramming in a hard-real-time environment[J].Readings in Hardware/Software Co-Design，2002，20（1）：179-194.

[6]Bertossi A A，Fusiello A.Rate-monotonic scheduling for hard-real-time systems[J].European Journal of Operational Research，1997，96（3）：429-443.

[7]Bastoni A，Brandenburg B B，Anderson J H.An empirical comparison of global，partitioned，and clustered multiprocessor EDF schedulers[C]//IEEE Real-Time Systems Symposium，2010：14-24.

[8]Leung J Y T，Whitehead J.On the complexity of fixedpriority scheduling of periodic，real-time tasks[J].Performance Evaluation，1982，2（4）：237-250.

[9]Andersson B，Tovar E.The utilization bound of nonpreemptive rate-monotonic scheduling in controller area networks is 25%[C]//IEEE International Symposium on Industrial Embedded Systems，2009：11-18.

[10]Baruah S K.The non-preemptive scheduling of periodic tasks upon multiprocessors[J].Real-Time Systems，2006，32（1/2）：9-20.

[11]George L.Preemptive and non-preemptive real-time uniprocessor scheduling，RR-2966[R].HAL-INRIA，1996.

[12]Nasri M，Brandenburg B B.Offline equivalence：A nonpreemptive scheduling technique for resource-constrained embedded real-time systems[C]//Real-Time and Embedded Technology and Applications Symposium，2017.

[13]Lee J.Improved schedulability analysis using carryin limitation for non-preemptive fixed-priority multiprocessor scheduling[J].IEEE Transactions on Computers，2017，66（10）：1816-1823.

[14]Andrei S，Cheng A M K，Radulescu V.An improved upperbound algorithm for non-preemptive task scheduling[C]//International Symposium on Symbolic and Numeric Algorithms for Scientific Computing，2015：153-159.

[15]Jeffay K，Stanat D F，Martel C U.On non-preemptive scheduling of period and sporadic tasks[C]//Proceedings of Twelfth Real-Time Systems Symposium，1991：129-139.

[16]Garey M R，Johnson D S.Computers and intractability：A guide to the theory of NP-completeness[M].New York，N Y：W H Freeman&Co，1979.