集成散度的MKL模型在模拟电路诊断中的应用
2018-05-08许爱强
张 伟,许爱强
ZHANG Wei,XUAiqiang
海军航空大学 航空作战勤务学院,山东 烟台 264001
School ofAeronautical Operations and Service,NavalAeronautical University,Yantai,Shandong 264001,China
1 引言
现代电子技术的快速发展,对模拟电路的测试与诊断提出了新的要求。由于元件参数的容差性、故障模式的多样性、广泛存在的非线性,使得传统的故障诊断方法在实际模拟电路诊断中难以达到预期的效果[1-2]。为此,针对模拟电路的故障特点,国内外学者开展了大量的研究,其中基于核的智能诊断方法取得了广泛的肯定和积极的研究成果[3-6],例如支持向量机(Support Vector Machine,SVM)、核超限学习机(Kernel Extreme Learning Machine,KELM)等。该方法将故障诊断问题建模为模式识别问题,通过对电路的正常模式和故障模式进行学习,构建诊断模型,最终形成诊断策略。
尽管基于核的诊断方法展示出优越的性能,但是核函数、核参数的选择严重制约着其有效性。近些年,大量研究表明,多核学习(Multiple Kernel Learning,MKL)是一种灵活性更强、解释能力更好的学习方法[7-8]。文献[4-5,9-10]已经将其应用到模拟电路等系统的故障诊断中,并通过大量实例证明在面对单故障、多故障以及并发故障时均能取得更高的诊断精度。在MKL中,为避免基核权重的缩放与初始化问题,通常一个范数约束被施加到基核权重上[11]。无论怎样,为一个给定的学习任务选择一种合适的范数约束本身就是一个开放性的问题。
近些年,在MKL中一个新兴的研究热点是通过最小泛化误差界来学习基核组合系数。在这些工作中将核导出空间中包含所有训练样本的最小闭球(Minimum Enclosing Ball,MEB)半径纳入MKL中。文献[12]构造了一个集成半径信息的MK-SVM模型,该模型被证明可以有效解决上文提到的缩放与初始化问题,从而避免了范数约束形式的选择问题。文献[13]提出一种融合半径信息的MK-ELM模型。该模型在继承融合半径信息的MK-SVM优点的同时,兼具了ELM计算高效的特点。但无论怎样,它也存在一些问题:(1)MEB半径对外部干扰极其敏感;(2)KELM中并不存在所谓的半径-间距界理论,将MEB半径强行引入MK-ELM,缺乏基本的理论依据。
为此,结合模拟电路故障特点,本文通过分析多核特征空间中的类内散度特性,设计了一种集成散度的自适应正则化MK-ELM模型。通过模拟电路诊断实例证明了所提方法的有效性、适用性。
2 多核特征空间的类内散度
在MKL框架下,设 {kq(⋅,⋅)}rq=1为选择的r个基核;为对应于r个基核的特征映射为给定任务下基核对应的核矩阵。则多核特征映射、组合核函数、组合核矩阵分别表示为:

对于一组具有c种模式的故障数据集,假设第l类故障样本个数为nl,且,n表示故障样本总数。则在组合核函数 k(⋅,⋅;γ)导出的特征空间中,训练样本的类内散度矩阵如下式所示:
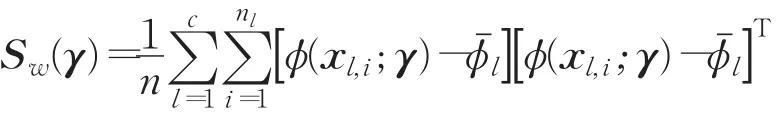
不失一般性,将故障样本的类内散度特性定义为类内散度矩阵的迹,记作Scatter-P=tr[Sw(γ)]。利用核技巧,进一步有:

3 集成散度的自适应正则化MK-ELM模型
3.1 新的优化目标函数
设训练数据和测试数据分别为DTr和DTe。令。其中,xi∈ℝd表示训练数据实例;d∈ℝ表示xi的维数;yi∈{1,2,…,c}表示xi对应的故障模式。令。其中,x′j∈ℝd表示测试数据实例;y′j未知。诊断模型设计的目的就是基于DTr去寻找一个映射函数 f(⋅):ℝd→ℝ ,使其可以将 DTe中的 x′j映射为相应的故障模式。当采用一般的MK-ELM作为诊断模型求解映射函数 f(⋅)时,其初始优化问题表示为:

假设在优化问题(3)所示的MK-ELM框架下存在一个区别于原始r个基核的虚拟基核,定义其对应的特征映射、核函数、核矩阵分别为:

式中,ei是一个n维的行向量,且第i个元素为1,其余元素为0;δ(i-j)为单位冲激函数,当i=j时等于1,否则为0;I是一个n阶的单位矩阵。
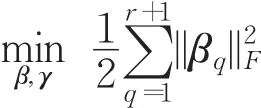
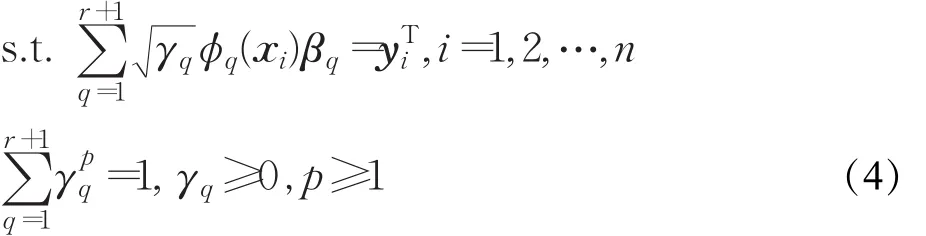
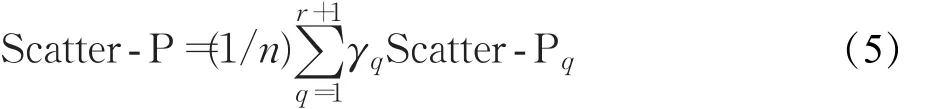
将式(5)纳入式(4)中,进一步得到:
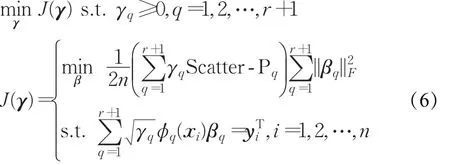
在优化问题(6)中有两个显著的改进:(1)通过引入虚拟基核,将正则化因子融入基核权重优化过程中,避免了基于交叉验证的正则化因子选择过程;(2)通过将Scatter-P集成到MK-ELM中,使得在最小化训练误差的同时最小化类内离散性,一方面赋予了优化过程更加明确的物理意义;另一方面则继承了集成MEB半径方法的优良特性。
定理1设τ为任意的正标量,对于式(6)所示的目标函数有 J(γ)=J(τγ),并且MK-ELM模型的决策函数值不受τ的影响。

可以看到,目标函数(8)与目标函数(6)具有相同的形式,所以二者具有相同的目标值,即 J(γ)=J(τγ)。设目标函数(6)的最优解为 β∗,则目标函数(7)的最优解为
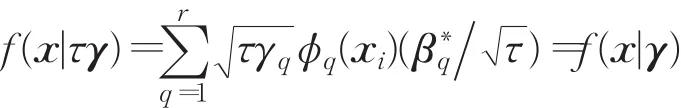
所以模型的决策值不会随着基核权重γ的缩放而发生改变。证毕。根据MK-ELM的决策函数,进一步有:
定理2设有两个不同范数约束的优化问题:
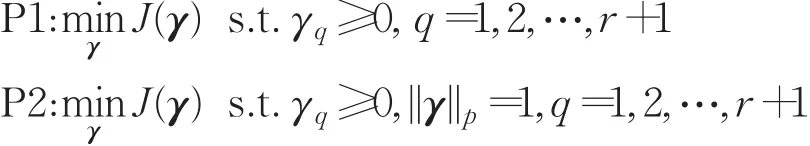
式中,||⋅||p表示向量的 p范数。如果是问题P2的最优解,那么必定是问题P1的最优解。
3.2 模型参数求解



由定理2,若问题(10)的最优解为 η∗,则问题(9)的最优解也为 η∗。再由定理1,J(η)=J(τγ)=J(γ),所以问题(6)和(9)具有相同的目标值,且当问题(9)的最优解为η∗时,问题(6)对应的最优解为:

同理,将γ∗代入MK-ELM决策函数中,显然有。所以,通过解优化问题(10)来替代解优化问题(6),最终决策函数值不变。
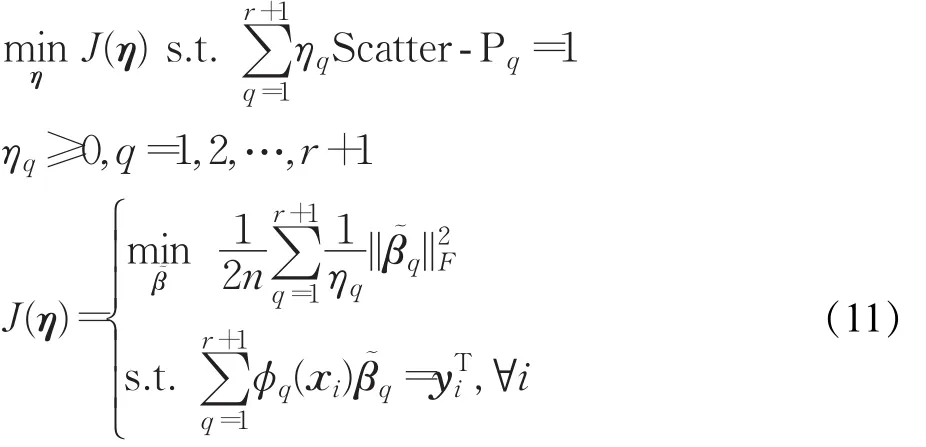
式中,α 和 λ均为拉格朗日乘子,且 α=[α1,α2,…,αn]T,。为了求解模型参数,采用一种两步交替优化的策略。
3.2.1 给定η的条件下求解α
将式(12)代入式(13)中,得到:

式中,Y表示标签矩阵,且Y=[y1,y2,…,yn]T。
3.2.2 给定α的条件下更新η
式中,ηq表示第q个基核在上一次迭代中的权重表示第q个基核在当前迭代中的权重。将代入到式(15)中即可得到新的组合权重
3.3 模型决策
当通过3.2节获得最优解α∗,η∗后,MK-ELM的决策函数表示为:

4 模拟电路故障诊断实施框架
4.1 故障电路生成与故障数据仿真
在故障电路生成阶段,通过变异生成操作将多种故障注入到被测电路(Circuit Under Test,CUT)中,得到一系列不同故障模式下的CUT变异体,故障生成所采用的变异操作如表1所示。其中,PCH为软故障变异操作,令ε为元件容差值,Θ为标称值,用均匀分布U(0.1Θ,Θ(1-ε))和 U(Θ(1+ε),2Θ)分别表示元件的参数负向偏差和正向偏差;ROP、LRB、GRB和NSP为硬故障变异操作,采用均匀分布 U(100 kΩ,1 MΩ)和 U(10 Ω,1 kΩ)分别表示开路状态和桥接状态对应的阻值。将生成的CUT变异体输入到基于Pspice的仿真器中,以扫频信号为激励,得到各CUT的频率响应曲线作为原始数据集。

表1 变异操作
4.2 故障特征提取
设原始特征集合为FT={g1,g2,…,gnum}。其中,gs表示第s个特征,num表示特征的个数。通过4.1节,每一类故障都有一个基于FT的num×nl的数据集Dl,记。其中,Dl(gs)表示第l类故障在特征gs上的数据集。而gs在所有故障上的数据集记作
定义1(故障特征间一维模糊度)给定两个故障Fa和Fb及其各自在特征gs上的概率密度函数(x)和Fa和Fb在特征gs上的一维特征模糊度定义为两条概率密度函数曲线的重叠部分与x轴围成区域的面积,如图1所示,记作:

图1 模糊度示意图
定义2(故障特征辨识力)给定两个故障Fa和Fb及其在特征gs上的一维特征模糊度,则 gs对这两类故障的辨识力定义为;进一步,gs对所有故障模式的辨识力定义为:

定义3(故障特征间的相似度)给定两个特征gs、gt及其在所有故障模式上的数据集 X(gs)和 X(gt);则gs与gt的相似度定义为X(gs)与X(gt)的皮尔逊相关系数[14],即:

假定需要选择d个特征,用FTd表示最终的特征集合。基于定义2、3,结合最小冗余最大相关准则,首先令;然后采用增量搜索算法依次去寻找满足优化条件的特征[15-16]。假设已经得到一个子集FTd-1,当前需要从{FT-FTd-1}中选出第d个特征,则对应的优化条件表示为:
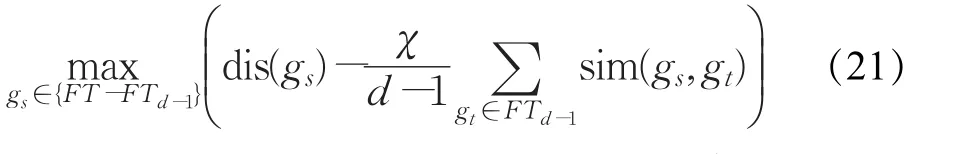
式中,χ>0是一个惩罚因子,用于平衡两个条件之间的重要性。通过上述的增量搜索过程,最终一组具有预定规模的特征集合能被获得。
4.3 故障模式分类
为表示方便,将提出的集成特征空间类内散度的自适应正则化多核诊断模型记作SiAMK-ELM(Scatterincorporated Adaptation MK-ELM)。下面将基于SiAMKELM的诊断流程总结如下。
步骤1输入原始仿真数据;设置特征选择个数d;惩罚因子 χ;基核 {kq(⋅,⋅)}以及虚拟基核 kr+1(⋅,⋅)。
步骤2由定义1计算Fa和Fb在gs上的一维特征模糊度。由定义2计算gs的辨识力dis(gs)(s=1,2,…,num)。由定义3计算特征gs和gt之间的一维相似度sim(gs,gt)(s,t=1,2,…,num ;s≠t)。
步骤4根据特征集FTd生成训练样本集DTr;令h=0,ηh=[1/r,…,1/r,1/C]。计算训练样本对应于基核的核矩阵;利用公式(5)计算基核诱导的特征空间中类内散度特性
步骤6根据特征集FTd生成测试样本集DTr;对于测试数据实例 x′j,计算 kq(xi,x′j)(i=1,2,…,n ;q=1,2,…,r);利用公式(16)计算 f(x′j);利用公式(17)得到x′j所对应的故障标签label(xj)。
5 实验仿真
为证明所提方法有效性,将其与KELM、SVM、SimpleMKL[17]、R-MKL[12]及文献[4,6]中的方法分别进行比较。实验中,单核方法采用高斯核函数,正则化参数与核参数通过网格搜索法得到;多核方法的正则化参数通过5折交叉验证得到。基于SVM的算法在处理多分类问题时采用“一对一”的策略;各种方法的诊断性能通过下列指标共同评价。
(1)错正率(False Positive Rate,FPR)=发生的漏警数/测试的故障样本总数。
(2)错负率(False Negative Rate,FNR)=发生的虚警数/测试的正常样本总数。
(3)故障命中率(Precision)=正确检测到的故障样本总数/检测到的故障样本总数。
(4)故障检测率(Fault Detection Rate,FDR)=正确检测到的故障样本总数/测试的故障样本总数。
(5)分类正确率(Accuracy)=分类正确的样本总数/测试的样本总数。
5.1 Sallen-Key带通滤波电路
该电路被用于详细分析SiAMK-ELM模型的诊断性能,其电路结构如图2所示。
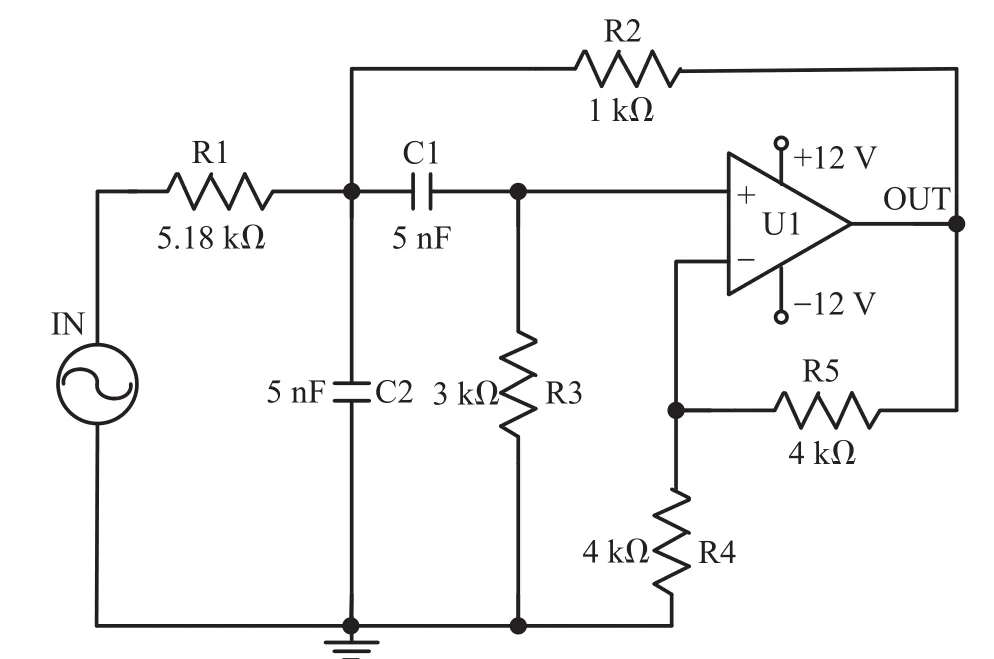
图2 Sallen-Key带通滤波电路
仿真实验共注入14种软故障,故障描述如表2所示。

表2 Sallen-Key带通滤波电路故障描述
实验中扫频信号设置为1 Hz~100.1 kHz,最终得到每种故障样本数为200,样本特征数为1 001的原始数据集。将其平分为2组,分别作为训练和测试数据集。令χ=0.8,提取出该CUT的诊断特征为FT21=[0.001,9.31,16.12,16.82,17.02,17.42,17.62,18.22,18.32,19.32,20.42,20.82,21.92,23.02,27.73,30.13,30.23,33.33,33.43,70.87,71.37]kHz。多核设置为 1个线性核,3个多项式核(参数分别为1,2,3)和8个高斯核(参数分别为1,2,4,6,8,10,12,14)。采用所有算法分别对该CUT进行诊断,提出的SiAMK-ELM的诊断结果如图3所示。

图3 SiAMK-ELM的诊断结果
由图3看到,SiAMK-ELM对本案例中的各类故障模式均有较好的区分能力,对所有故障模式的平均诊断正确率达到96.4%。其中,对F3、F7、F10和F14均实现了100%的诊断正确率;诊断正确率最低的是F8,其对应的正确率为84%。
表3给出了SiAMK-ELM与单核诊断方法的诊断性能比较。由表3看到:(1)对于诊断精度,相比于三种单核方法,SiAMK-ELM将其分别提升了5.13%、7.87%和4.28%。(2)对于时间花费,SiAMK-ELM由于要解多核优化问题,因此需要花费更长的时间。(3)对于FPR、SiAMK-ELM较KELM降低了1.36%;对于FNR、SiAMKELM较SVM降低了5%;实现了对漏警、虚警的有效均衡。

表3 与单核诊断方法的诊断性能比较
表4给出了SiAMK-ELM与多核诊断算法的诊断性能比较。由表4看到:(1)在诊断精度上,相比于其余三种算法,SiAMK-ELM将诊断精度分别提升了1.60%、0.60%和0.53%,得到了与其他算法近似一致的诊断精度。(2)在时间花费上,其余三种MKL算法的训练时间分别是SiAMK-ELM的2.10倍、3.60倍和1.84倍。究其原因,首先,ELM作为一种快速的分类算法,相比于SVM更加高效。其次,在SiAMK-ELM中不需要对基核权重施加任何范数约束,优化过程更加简洁。再次,SiAMK-ELM中由于正则化因子的自适应调整保证了算法可以更快地达到收敛。
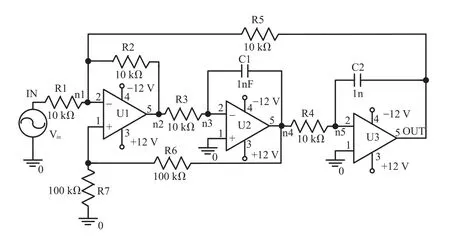
图4 Biquad低通滤波电路

表4 与多核诊断方法的诊断性能比较
5.2 Biquad低通滤波电路
该电路被用来验证SiAMK-ELM对不同属性电路故障的诊断能力,电路结构如图4所示。仿真实验共注入故障29个,故障描述如表5所示。

表5 Biquad低通滤波电路故障描述
通过模糊度分析发现,ROP、LRB变异操作下的各故障模式与正常模式的频率响应曲线极其相似。图5展示了F0与F18在4个频点上的模糊度值,显然,F18与F0很难被区分。为了处理该问题,本节引入响应曲线簇模糊组定义。
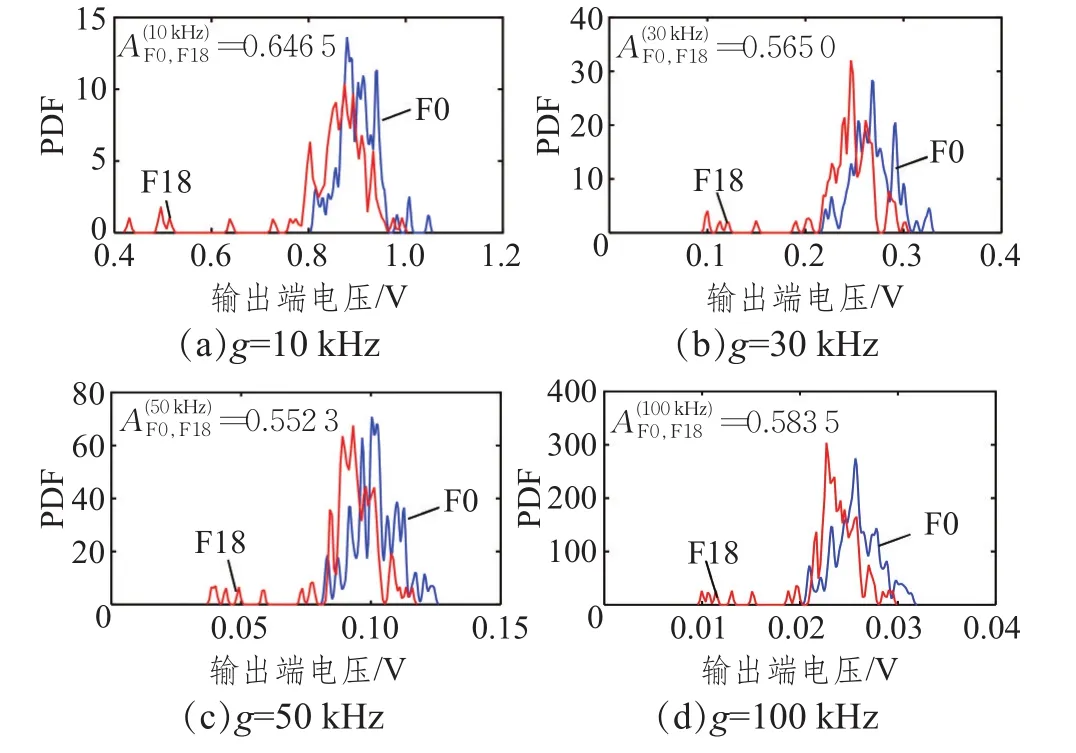
图5 F0和F18在4个频点上的模糊度值
定义4(响应曲线簇模糊组)给定故障Fa和Fb,二者间的最小模糊度定义为设置阈值ν∈[0,1],若Fa和Fb的最小模糊度满足 A∗a,b≥ν,则称这两个故障构成一个响应曲线簇模糊组。
通过依次设置 ν等于1.0、0.7、0.5、0.3和0.1,Biquad低通滤波电路的模糊组如表6所示。

表6 不同门限下Biquad电路模糊组
实验中得到每种故障样本数为100,样本特征数为1 000的数据集。将其平分为两组,分别作为训练和测试数据集。令χ=1,提取出该CUT的诊断特征为FT25=[7.609,10.61,13.01,14.02,14.62,14.82,15.02,15.22,15.42,15.62,15.82,16.02,16.22,16.42,16.62,16.82,17.02,17.22,17.42,17.62,17.82,46.25,46.65,199.8,200]kHz。多核设置为1个线性核,3个多项式核(参数分别为1、2、3)和8个高斯核(参数分别为1、2、4、8、12、60、100、140)。假设只要诊断结果为实际故障所在模糊组中的任意一种故障则认为诊断正确。不同ν值下各方法的诊断精度如表7所示;而诊断的FNR、FPR、Precision和FDR分别如图6所示。
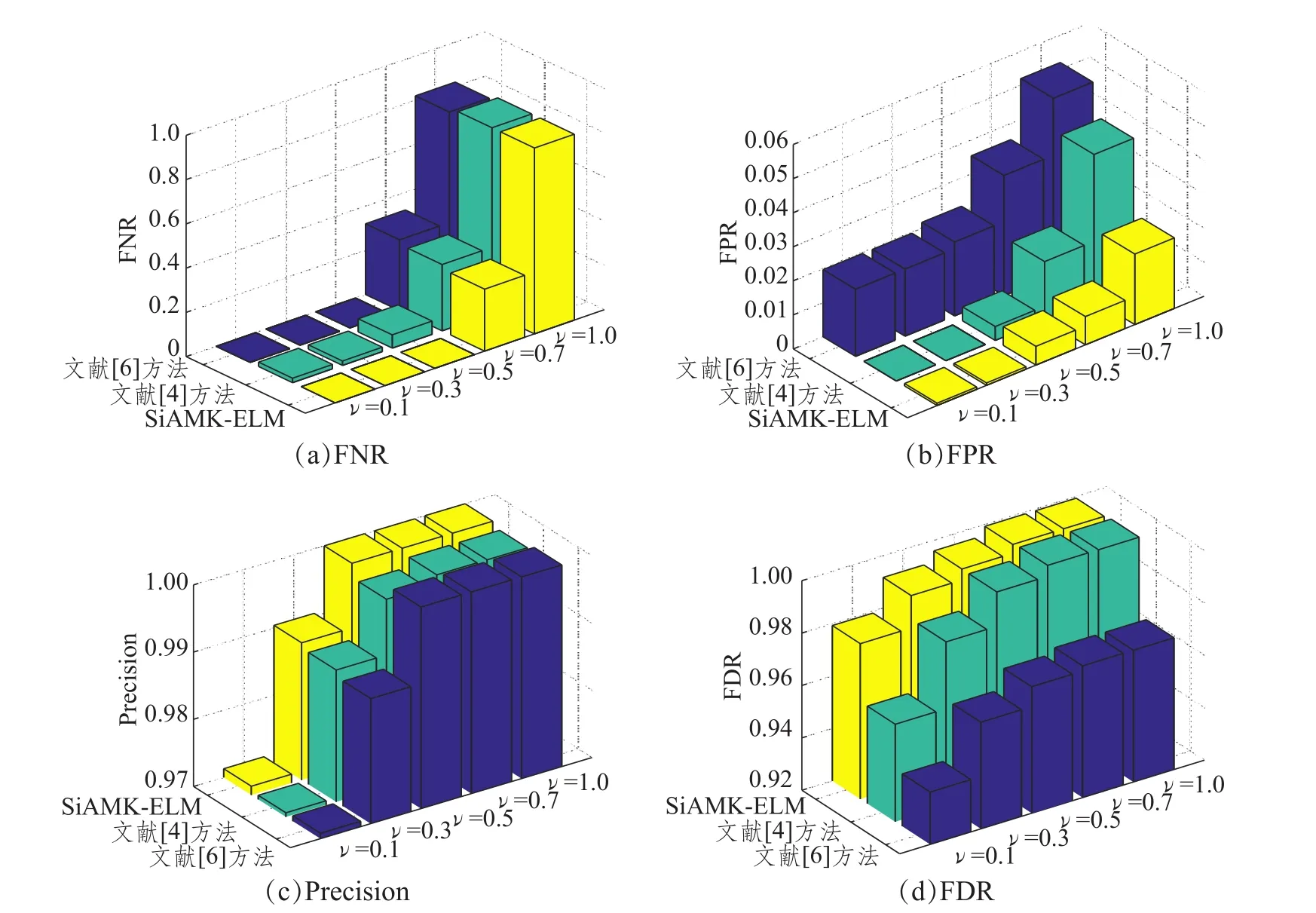
图6 Biquad低通滤波电路诊断结果比较
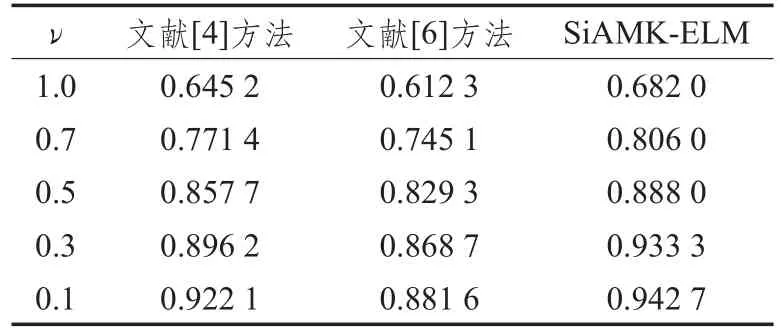
表7 Biquad低通滤波电路诊断精度比较
通过表7和图6可以看到:(1)当ν=1,即不考虑模糊组时,三种方法的诊断正确率都比较低,而且虚警率很高,正如提到的F18,此时许多故障模式与正常模式难以被区分。(2)随着ν的降低,具有相似特征的故障模式落入同一模糊组中。当考虑模糊组时,三种方法的诊断准确率随着ν的减小而上升。在不同的模糊组门限下,SiAMK-ELM具有最高的诊断正确率,当ν=0.5时,其诊断正确率已达到88.8%,甚至高于ν=0.1时文献[6]的诊断精度。(3)在图6中,SiAMK-ELM在不同ν下具有更低的FNR和FPR,同时具有更高的FDR和Precision,该结果进一步证实了所提方法的有效性。
6 总结
通过故障注入生成参数连续的各类软故障和硬故障,并考虑非故障元件的参数容差,本文提出一种新的模拟电路故障诊断方法。针对两个CUTs的诊断实验,得到下列结论:
(1)相比于单核诊断方法,所提方法在平衡漏警、虚警的同时,能够显著提升诊断的正确率。当引入模糊组概念时,能够将难以辨识的故障样本更加准确地隔离到相应模糊组中。
(2)相比于一般的多核诊断方法,所提方法在获得相似甚至更高的诊断正确率的同时,能够有效约减诊断时间花费。
(3)所提方法在MKL基础上将正则化因子直接纳入多核优化过程中,因此不需要额外的参数选择过程,人为干预因素少,便于操作。
参考文献:
[1]Han H,Wang H J,Tian S L,et al.A new analog circuit fault diagnosis method based on improved mahalanobis distance[J].Journal of Electronic Testing,2013,29(1):95-102.
[2]颜龙,丁鹏,马峻.基于狼群算法的RBF神经网络模拟电路故障诊断[J].计算机工程与应用,2017,53(19):152-156.
[3]Tang X F,Xu A Q.Practical analog circuit diagnosis based on fault features with minimum ambiguities[J].Journal of Electronic Testing,2016,32(1):1-13.
[4]Zhang C L,He Y G,Yuan L F,et al.A novel approach for diagnosis of analog circuit fault by using GMKLSVM and PSO[J].Journal of Electronic Testing,Theory and Applications,2016,32(5):531-540.
[5]Ye F M,Zhang Z B,Chakrabarty K,et al.Board-level functional fault diagnosis using multikernel support vector machines and incremental learning[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2014,33(2):279-290.
[6]高坤,何怡刚,谭阳红,等.主成分分析和超限学习机的模拟电路故障诊断[J].计算机工程与应用,2016,52(9):248-252.
[7]Liang Z Z,Zhang L,Liu J.A novel multiple kernel learning method based on the Kullback-Leibler divergence[J].Neural Process Lett,2015,42:745-762.
[8]张钢,谢晓珊,黄英,等.面向大数据流的半监督在线多核学习算法[J].智能系统学报,2014,9(3):355-363.
[9]Ye Q,Pan H.Simultaneous fault diagnosis of main retarder using improved paired relevance vector machine based on multi-kernel learning[J].Applied Mechanics and Materials,2014,614:339-344.
[10]Li Y X,Ren C Q,Bo J Y,et al.The application of GMKL algorithm to fault diagnosis of local area network[J].Journal of Networks,2014,9(3):747-753.
[11]Kloft V,Brefeld U,Sonnenburg S,et al.lp-norm multiple kernel learning[J].Journal of Machine Learning Research,2011,12:953-997.
[12]Gai K,Chen G Y,Zhang C S.Learning kernels with radiuses of minimum enclosing balls[C]//Advances in Neural Information Processing Systems,2010:649-657.
[13]Liu X W,Wang L,Huang G B,et al.Multiple kernel extreme learning machine[J].Neurocomputing,2015,149:253-264.
[14]Chudzian P.Evaluation measures for kernel optimization[J].Pattern Recognition Letters,2012,33:1108-1116.
[15]Wu P,Duan F Q,Guo P.A pre-selecting base kernel method in multiple kernel learning[J].Neurocomputing,2015,165:46-53.
[16]Peng H C,Long F H,Ding C.Feature selection based on mutual information:Criteria of max-dependency,max-relevance,and min-redundancy[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1226-1238.
[17]Rakotomamonjy A,Bach F R,Caun S,et al.SimpleMKL[J].Journal of Machine Learning Research,2008,9:2491-2521.
