危险化学品仓库堆垛安全布局建模及优化研究*
2018-05-08李雁飞陈增强安海洋任海胜
戴 波,李雁飞,陈增强,安海洋,2,任海胜,2
(1.北京石油化工学院 信息工程学院,北京 102617;2.北京化工大学 信息科学与技术学院,北京 100029)
0 引言
危险化学品作为化工生产的重要物资,在整个工业体系发挥着重要作用,因其有毒性、腐蚀性以及易燃易爆等特性[1],在对其进行仓储过程中对仓库选址、堆垛方式、五距(墙距、垛距、灯距、通道距和柱距)等方面有明确要求[2-3]。据有关分析,我国发生的危化品事故存储环节事故量位居全球第二,造成了重大的生命财产损失和广泛的社会影响,在危化品工业进园区的大趋势下,加强对危化品行业监管,将安全管理放在首位,做好危化品仓库的安全布局优化工作对减少危化品事故隐患有重要作用[4-5]。
为了在满足要求的基础上提高仓库利用率,可通过优化布局算法对危险化学品仓库进行布局设计。现有的布局优化方案大多适用于集装箱或板材切割等密集布局,关于危化品仓库的布局研究多数是关于选址和宏观规划,Song等[6]通过引入潜在生命损失的评价指标,提出了危险化学品的仓储选择和安全布局优化方法,但是其布局优化更多的是停留在仓库选址和分布的意义上,并没有具体到危险化学品的摆放准则;Xu等[7]通过使用混合整数优化的方法基于构建方案来确定最优布局(即坐标和尺寸),解决危化品工程工厂的布局问题,对于仓库堆垛具有借鉴意义,不同的是堆垛的布局优化拥有更为严格和细碎的准则。危险化学品仓储的布局优化需要考虑多种复杂约束的多目标组合优化问题,属于NP难问题,是一个具有综合性、跨学科的研究课题,是当前需要被研究的重点,对于理论研究和现实需求而言,其意义十分重要。
对于矩形布局问题的求解主要有3大类方法:一是应用分块模式对大矩形空间进行模块划分,利用动态规划算法对待布小矩形进行排样,应用隐式枚举法试算所有可能的分块组合,最终找到利用率最高的布局方案[8-10],此类算法主要用于解决同尺寸布局问题;二是应用启发式算:蚁群算法[11]、遗传算法[12-13]、粒子群算法[14]等首先得到待布物体排放顺序,进一步采用下台阶算法、剩余矩形法和最低水平线等规则将待布物体布入,将算法改进后综合应用可以得到更高的利用率[15],此类算法可以有效解决不规则布局问题;三是采用整数线性规划方法将布局问题转化成数学问题,提出1种数学模型,通过线性化处理对其进行求解,模型中约束条件和目标函数在问题类型不同时有差别[16]。
现有的优化方案可以解决集装箱堆垛或者矩形板材切割等密集布局问题。对于危险化学品仓库,其主要特点是仓库内危险化学品的摆放要在满足五距,物流效率的基础上提高仓库利用率,现有的布局方案无法满足五距和通道的要求。因此,针对危化品仓库的特点,建立1种危化品堆垛安全布局的模型,寻求1种安全高效的布局优化方案很有必要。危化品的贮存类别有露天、隔离、隔开和分离等。在工业安全中,不同类型的危险化学品具有严格的混存规则,现实应用中应当尽可能避免混存现象的发生。本文主要研究存放同种类型的危化品仓库的布局,在此基础上可进一步开展其他贮存方式的优化研究。
1 危化品堆垛安全布局优化数学模型
对危化品仓库堆垛安全布局问题进行建模,首先应对该问题有准确的数学描述。对于集装箱优化装载问题的描述,主要分一维、二维和三维3类,一维装箱算法直接用线段的长度进行描述;二维装箱算法比较灵活,根据布局方法和策略采用不同描述方法,分为采用物品左下顶点的Y值坐标、不同长度线段和层编号表示的分层描述及用矩形的二维坐标及长度宽度信息描述的非分层描述;三维装箱算法[17-18]大多利用待装箱体的顶点坐标进行表示。
一般的危化品仓库为保证安全,避免危险化学品和地面直接接触,将其存放于苫垫上。对此,应用分层的思想,首先,对苫垫在仓库内的排放进行布局优化;其次,对其上危险化学品的堆垛摆放进行布局优化;最终,完成仓库整体布局。
1.1 问题描述
对于危险化学品的贮存,一般采用矩形箱体或者圆柱形容器,堆垛在苫垫上,苫垫下垫高150~300 mm,宜堆小垛,保证安全的墙距、柱距、垛距、顶距、灯距等五距。具体描述如下:
现有一长度为L0,宽度为W0,高为H0的危化品仓库,拟存放贮存方式为矩形箱体的某危险化学品A,包装尺寸为l1×w1×h1,矩形箱体的某危险化学品B,包装尺寸为l2×w2×h2,…,数量待定。现将危险化学品放入仓库,在保证安全的情况下,提高仓库利用率。排放方式要满足以下几点:
1)每个堆垛单元不得重叠覆盖;
2)所有堆垛单元必须在仓库之内;
3)考虑到搬运的便利性,所有堆垛单元正交排放在仓库内;
4)根据仓库实际情况确定主通道和辅通道。
1.2 数学模型
危险化学品仓库不同于普通仓库,需要从仓库利用率、安全距离、通道设置和周转效率等方面考虑,基于此建立一种危化品仓库堆垛安全布局模型,描述如下:

(1)
式中:Xi⊗Pi表示第i种危化品布局方式;t表示危化品总种类;S为布局结果评价函数;M为主通道占地面积,m2;M0为其他占地,m2,如柱子等;w,s,c,t,l,d分别为墙距、垛距、柱距、顶距、灯距、辅通道宽度,m。
布局结果的优劣通过评价函数来衡量,在此基础上,本文针对小型危险化学品仓库采用分层的思想将仓库布局问题转化为二维布局。仓库内柱子的主要设计依据包括建筑物的楼层数、楼层高度、地盘载重、抗震能力等,另外还需考虑仓库保管效率及作业效率,仓库内柱子暂时不做考虑,即M0为0,柱距为0;二维布局不涉及垂直方向的灯距和顶距,所以本文中主要考虑的安全距离是墙距、垛距和通道距。针对存放单一种类的危化品仓库建立数学模型:
以仓库面积利用率f作为目标(评价)函数S:
(2)
约束条件为:
(3)
式中:L0,W0分别表示矩形仓库的长和宽,m;L1,W1分别表示每个堆垛单元的长和宽,m;D,d分别表示仓库内主通道和内辅通道宽度,m;w,s,c,t,l分别表示墙距、垛距、柱距、顶距和灯距,m;m为W0方向长度为L1的堆垛单元数量,个;n为W0方向长度为W1的堆垛单元数量,个;p为L0方向长度为L1的堆垛单元数量,个;q为L0方向长度为W1的堆垛单元数量,个;r为辅通道数量,个。
2 仓库堆垛通道及矩形区域布局分层优化算法
仓库内的堆垛单元、通道排布问题可看作矩形排样问题,矩形排样问题是典型的组合优化问题,已被认定为NP完全问题,该类问题的特征是无法在有限合理的时间内求得其精确解,只能依赖近似算法。加之布局问题种类繁多,求解复杂,所以目前国内外研究方法主要分2类,一种是将布局问题转化成某种数学模型,对该模型进行精确求解;另一种是应用启发式算法得到近似最优解[19-20]。
危险化学品仓库的布局问题与矩形布局问题有以下明显差异:
1)待布局危险化学品数量无限多;
2)待布局危险化学品堆垛大小不确定;
3)危险化学品的布局要满足五距要求;
4)仓库中必须有便于危险化学品运输的主通道和供工作人员通过进行日常检查的辅通道。
为实现对危险化学品仓库的布局问题求解首先要对其中的安全距离、通道和堆垛单元进行设计,进而应用矩形区域布局分层优化算法进行布局计算。
2.1 安全距离设计
为满足危化品仓储的五距要求,需要对布局过程中涉及的仓库矩形空间、堆垛单元和通道作出改进,以保证在满足安全距离的要求上提高计算效率。
1)垛距


图1 垛距示意Fig.1 The distance of the stamping
对于存在空间柱体的情况,柱距根据实际尺寸做相似改进。
2)墙距

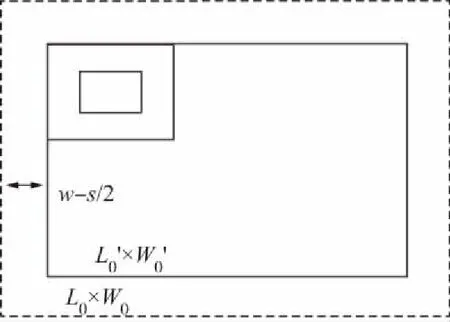
图2 墙距示意Fig.2 Wall distance diagram
3)顶距和灯距
顶距是堆垛单元顶面与仓库房顶之间的距离,灯距是仓库内照明灯与堆垛单元垂直方向要满足的距离,本文对二维布局进行设计优化,暂不涉及。
通过这种改进,可以满足五距安全要求的基础上简化布局设计,提高布局效率。
2.2 堆垛单元设计
实际仓库内危化品都是堆放在苫垫上,将苫垫上的所有危化品货物视为一个堆垛单元。为实现仓库布局设计,首先,确定堆垛单元即苫垫的布局;其次,确定苫垫上危化品的布局放方式;最终,使仓库利用率最大。危化品仓库分为苫垫尺寸未知和已知2种情况。
1)苫垫尺寸未知
对于苫垫尺寸未知的危险化学品仓库,根据待存货物和搬运方式确定堆垛单元,进而确定苫垫尺寸。常见几种垛型如图3所示:

图3 垛型Fig.3 Stamp type drawing
堆垛单元的尺寸由垛型决定。
2)苫垫尺寸已知
对于确定尺寸的苫垫,堆垛单元大小已定,先对苫垫进行布局,然后根据苫垫尺寸对其上待放矩形货物进行优化布局,提高摆放货物的数量。
2.3 仓库堆垛通道设计
1)主通道
主通道的宽度设计主要考虑双向运输的原则,所以主通道D宽度要满足公式:
D=2B+C
(4)
M=D×L
(5)
式中:C是安全间隙,一般认为C=0.9 m;B为运输设备宽度,m,本文中B=max(l,w);M为主通道面积,m2;L为仓库横向长度,m。
仓库在使用过程中,运输便利性占很大比重,所以仓库内主通道的设计尤为重要。考虑到仓库的具体设计中,主通道必须是与门在同一水平线上,这样可以保证运输便捷的情况下减少不必要通道位置的浪费,增加可堆垛仓库面积。仓库门的位置没有确定,主通道在仓库中的位置处于可调状态,其位置的确定主要由通道两边可堆垛面积和仓库利用率决定。
2)辅通道
辅通道主要用来人工查看仓库内货物状况,一般设定宽度r=1.0 m。在实际仓库设计中,当每排堆垛单元数量只有一个的情况下,不设置辅通道,当数量大于1的时候设置辅通道,如图4所示。

图4 通道示意Fig. 4 Schematic diagram of channel
图4中主通道上方区域中,每排堆垛单元数量大于1,设置辅通道;下方区域中,每排只有1个堆垛单元,不设置辅通道。
2.4 矩形区域布局分层优化算法
采用分块模式对布局问题进行研究取得较好成果,其中最常用的是采用G4算法实现布局问题求解。该算法的理论基础是动态规划算法,采用G4结构对待布区域进行划分,在每次划分出的小区域调用子算法进行布局设计,利用最大边界、无重复枚举等定界策略来减少计算量,该种方法在同类矩形或集装箱布局问题上应用较多[21-23]。
如果矩形存在I={1,2,…,n}的一种划分,使得A(I1)与A(I2)形成一种G-结构块模式,称矩形的布局模型为G-结构;如果存在I={1,2,…,n}的一种划分将其分成q(q≥1)个分离的子集Ij,同时每一A(Ij)形成一个pj块结构,则称布局模式A为k-块结构。如果矩形P(L,W)的一种布局模式A具有k-块结构(k≤4),则称该布局模式为G4结构。
应用G4算法思想,对于矩形仓库采用G4结构划分,如图5所示:

图5 G4结构划分Fig.5 G4 structure division
主通道贯穿整个仓库空间,将矩形仓库分为2个矩形部分,对这2个矩形部分进行划分得到类G4划分,分别4个堆垛区域进行堆垛单元的布局,可以得到此种划分情况下最优布局方案,通过调整堆垛区域大小,得到不同的布局结果。
仓库内主通道位置没有明确规定,考虑到运输装卸便利性,其位置需在靠近矩形仓库中间的位置。采用动态规划思想,以其中一块区域为基准,确定面积及其中苫垫布局方式,则其相邻区域可以确定进而确定通道位置,之后计算通道另一侧区域中苫垫的布局方式;循环改变基准区域面积,得到不同的布局结果。对于苫垫的布局方式,首先,相邻区域采取同样布局方式,全部横放或者全部竖放,计算此时仓库利用率;其次,相邻矩形区域内的苫垫采用横竖交叉的摆放方式;最后,再计算此时仓库的利用率,根据约束条件筛选符合条件的仓库利用率最大的排放方式。
算法流程如图6所示。

图6 算法流程Fig. 6 Flow chart of algorithm
算法使用的筛选条件是主通道将仓库分成的上下2部分,面积比在0.5~2.0之间,以此寻找符合要求的仓库最大利用率摆放方式。可以防止通道位置太偏导致货物存放过于密集通风不良导致危险事故的发生,同时也可以提高货物的搬运效率。
3 危化品仓库堆垛安全布局方案计算
3.1 苫垫布局方案计算
假设存在面积为50 m×40 m的危险化学品仓库,用于存放的危险化学品包装尺寸为1.5 m×2.0 m×2.5 m,需要满足墙距0.3 m,垛距0.8 m,通道距0.3 m的要求。此类问题属于堆垛单元尺寸未知问题,因此,要根据货物尺寸,针对不同的垛型分别进行布局实验,最终选定利用率最高的方案。结果如图7所示。


图7 布局结果Fig. 7 Layout result chart
布局结果图中,空白区域表示未利用的空间。
基于7种垛型分别进行布局,危化品包装尺寸不变,继续对面积分别为70 m×70 m和130 m×100 m的仓库进行布局实验,得到仓库利用率结果如表1所示。
根据结果可以看出,在仓库面积为50 m×40 m时,仓库利用率最高的是第6种排布情况,70 m×70 m时,仓库利用率最高的是第6种排布情况,130 m×100 m时,仓库利用率最高的是第6种排布情况。仓库门的位置根据主通道位置确定,仓库内苫垫的布局根据给出结果确定,其上危险化学品的布局根据对应垛型确定。

表1 仓库利用率
3.2 堆垛布局方案计算
假设有一苫垫尺寸为11 m×9 m的危险化学品仓库,存放的危险化学品包装尺寸为2.5 m×1.5 m,属于堆垛单元尺寸已知的仓库布局问题,在使用布局算法时直接输入堆垛单元的尺寸即可完成对苫垫的布局,此时需要优化苫垫上危化品货物的布局,进而提高仓库利用率,应用前文算法,此时苫垫上货物的摆放可以有以下几种情况,如图8所示。
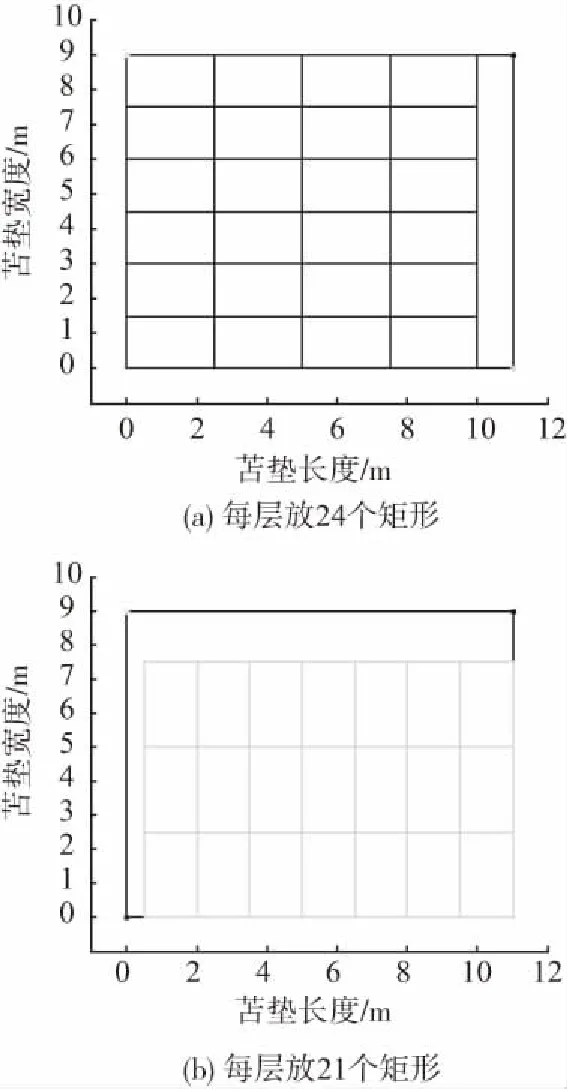

图8 堆垛布局结果Fig. 8 Results of stacking and stacking
图8中的图块表示危化品包装箱在苫垫上的布局位置。由图8上布局结果可以看出,在长11 m、宽9 m的苫垫里排放包装尺寸为长2.5 m、宽1.5 m的危化品,理论上可排放的危化品个数不超过26。采用一般排放方式全部横放如图8(a)所示,每层可以摆放24个矩形;全部竖放如图8(b)所示,每层可以摆放21个矩形;应用本文提出的算法,每个苫垫每层最多可以摆放26个矩形,有2种摆放方式,如图8中的(c),(d)所示。结果表明,本文提出的算法可以提高苫垫利用率进而提高仓库利用率。
4 结论
1)建立了危化品仓储堆垛安全布局优化数学模型,将布局问题转化成数学问题,方便优化研究。
2)结合分层优化的思想将仓库布局问题分成苫垫布局优化及其上危化品的布局优化,在已知仓库及其中存放的危化品的基本尺寸的情况下可以进行计算。
3)提出了1种采用G4结构划分,结合动态规划方法对仓库及苫垫进行布局的优化算法,通过调整通道位置可以得到较高利用率的仓库布局方案。
[1] 刘向东.探讨石化企业危化品仓库安全管理存在的问题及其对策[J].企业导报,2016(14):154.
LIU Xiangdong.Discussion on problems and countermeasures of safety management of dangerous chemicals warehouse in petrochemical enterprises [J].Guide to Business,2016(14):154.
[2] 李淑梅.浅析危险化学品的仓储管理[J].物流技术,2012(16):69-72.
LI Shumei.Analysis of warehousing and management of hazardous chemicals [J].Logistics Technology,2012(16):69-72.
[3] 全国危险化学品管理标准化技术委员会.常用化学危险品贮存通则:GB 15603-1995[S].北京:中国标准出版社,1996.
[4] 任继勤,穆咏雪.危化品事故的统计分析与管理启示[J].化工管理,2015(16):28-31.
REN Jiqin,MU Yongxue.Statistical analysis and management implications of hazardous chemicals [J].Chemical Industry Management,2015(16):28-31.
[5] 李健,冯云晓,于洋,等.“十二五”期间我国危险化学品事故统计及建议[J].武汉理工大学学报(信息与管理工程版),2016,38(5):543-547,552.
LI Jian,FENG Yunxiao,YU Yang,et al.Research on the statistics of hazardous chemical accidents in China during the “Twelfth Five-Year”period and Recom mandafions[J].Journal of Wuhan University of Technology(Information and Management Engineering),2016,38(5):543-547,552.
[6] 宋占兵.基于潜在生命损失的危险化学品仓储区规划选址和安全布局方法研究[J].中国安全生产科学技术,2013,9(11):37-42.
SONG Zhanbing.Study on site selection and safety layout of hazardous chemicals storage area based on potential loss of life [J].China Safety Science & Technology,2013 ,9(11):37-42.
[7] XU Gang,PAPAGEORGIOU L G.A construction-based approach to process plant layout using mixed-integer optimization [J].Industrial & Engineering Chemistry Research,2007,46(1):351-358.
[8] 易向阳,潘卫平,张俊晖.基于五块模式的单一矩形件排样算法[J].图学学报,2015,36(4):521-525.
YI Xiangyang,PAN Weiping,ZHANG Junhui.A single rectangle piecing algorithm based on five patterns[J].Acta Mechanica Sinica,2015,36(4):521-525.
[9] 潘卫平,陈秋莲,崔耀东,等.基于匀质条带的矩形件最优三块布局算法[J].图学学报,2015,36(1):7-11.
PAN Weiping,CHEN Qiulian,CUI Yaodong,et al.Rectangles and other pieces of rectangular strips based on homogeneous three optimal layout algorithm [J] FIG Science Journal,2015,36(1):7-11.
[10] 农健恒,崔耀东.同尺寸物品装箱的动态规划算法[J].计算机应用与软件,2014,31(7):249-251.
NONG Jianheng,CUI Yaodong.Dynamic programming algorithm for box packing of same size [J].Computer Applications and Software,2014,31(7):249-251.
[11] 宋真真.基于蚁群算法的布局问题研究[D].天津:天津职业技术师范大学,2016.
[12] 甄士刚,王金敏.一种基于评价函数的三维矩形布局遗传算法[J].天津职业技术师范大学学报,2014,24(1):9-12.
ZHEN Shigang,WANG Jinmin.A three-dimensional rectangle layout genetic algorithm based on evaluation function[J].Journal of Tianjin Vocational and Technical Teachers' University,2014,24(1):9-12.
[13] GONCALVES J F,RESENDE M G.A parallel multi-population genetic algorithm for a constrained two-dimensional orthogonal packing problem[J].Journal of Combinatorial Optimization,2011,22(2):180-201.
[14] 董辉,陈建军.改进粒子群算法在二维排样中的研究与应用[J].浙江工业大学学报,2016,44(4):388-391.
DONG Hui,CHEN Jianjun.Research and application of improved particle swarm optimization algorithm in two-dimensional layout [J].Journal of Zhejiang University of Technology,2016,44(4):388-391.
[15] GONCALVES J F,RESENDE M G.A parallel multi-population biased random-key genetic algorithm for a container loading problem[J].Computers & Operations Research,2012,39(2):179-190.
[16] 沈秀敏.基于整数线性规划方法的集装箱装载布局优化问题研究[D].大连:大连海事大学,2013.
[17] WEI Lijun,ZHANG Defu,CHEN Qingshan.A least wasted first heuristic algorithm for the rectangular packing problem[J].Computers & Operations Research,2009,36(5):1608-1614.
[18] 姚怡.二维装箱问题的启发式算法研究[D].广州:华南理工大学,2016.
[19] 翟鹏飞.基于遗传算法的矩形件分层排样问题研究[D].天津:天津大学,2012.
[20] 刘海明,周炯,吴忻生,等.基于改进最低水平线方法与遗传算法的矩形件排样优化算法[J].图学学报,2015,36(4):526-531.
LIU Haiming,ZHOU Jiong,WU Xinsheng,et al.A rectangular piece nesting optimization algorithm based on improved minimum horizontal line method and genetic algorithm [J].Journal of Graphics,2015,36(4):526-531.
[21] 孙洪礼,王周敬.同类货物集装箱装载问题的启发式算法[J].计算机应用与软件,2011,28(4):193-195,204.
SUN Hongli,WANG Zhoujing.Heuristic algorithm for container loading of similar cargo containers[J].Computer Applications and Software,2011,28(4):193-195,204.
[22] 马国通.两类矩形布局问题的启发式算法研究[D].北京:北京交通大学,2008.
[23] 吕盛坪.G4算法实现与布局问题的相对熵算法研究[D].北京:北京交通大学,2008.
