导向向量误差概率约束的宽容性波束形成

(浙江工业大学 之江学院，浙江 杭州 310024)

自适应波束形成虽然能够提高目标分辨力和干扰抑制能力，但是当阵列导向向量与目标的真实响应向量存在误差时，性能会急剧下降，甚至期望信号被看作干扰而受到抑制.对角加载方法[1](即白噪声增益控制方法)是最常用和最有效的宽容处理方法，而且易于实现，其缺点是难以确定合适的对角加载量.Li等[2-4]提出了一种在导向向量误差最大情况下，使性能最优的宽容处理方法，将自适应波束形成问题归结为在误差不确定性集合的边界上的约束优化问题.Li等[2]证明了文献[2-4]的方法都等效于对角加载方法，不同之处在于加载量的确定方法不同，Lorenz等[3]采用有效的Lagrange(拉格朗日)法，而Vorobyov等[4]采用了计算较为复杂的二阶锥规划方法，限制了其实用性.概率约束方法[5]减小了误差最大情况下性能最优化方法的局限性，因为误差最大情况实际并不总能出现，Li等[2-4]方法在模型无失配的情况下将会使背景噪声电平升高，分辨力下降.He等[6]分析了概率约束方法和Li等[2-4]方法的关系，即对角加载量之间的关系.笔者综合考虑分辨力和宽容性，研究导向向量误差概率约束的宽容算法，波束形成性能的优化不局限在不确定性集合的边界上，而是在误差变化集合的内部寻找最优权向量，有助于提高导向向量误差较小情况下的性能.

1 背景知识

1.1 常规自适应算法

考虑M元均匀线列阵，间距为d，接收到空间L个远场窄带平面波信号，阵列接收信号的第k个采样可表示为

(1)

式中：si(k)为第i个信号源的第k个采样；x(k)=[x1(k),x2(k),…,xM(k)],T为M×1维阵列输出信号向量；n(k)=[n1(k),n2(k),…,nM(k)],T为M×1维加性噪声向量；A为M×L维阵列导向矩阵，A可表示为A=[a(θ1),a(θ2),…,a(θL)]，θi为第i个信号源的入射方向(相对正横方向)，a(θi)为相应的阵列导向向量，其第m个元素(即第m个阵元对θi方向的单位幅度复信号的响应)可表示为

am(θi)=exp[j2π(m-1)dsinθi/λ]

式中：d为阵元间距；λ为信号波长.

设a=a(θ)为阵列对期望信号的导向向量，则基于样本矩阵求逆(Sample matrix inversion, SMI)的自适应波束形成[1]可表述为

(2)

利用Lagrange法可得自适应权向量为

(3)

当导向向量a(θ)与第i个入射信号的响应向量a=a(θ)一致时，θi方向的波束输出信号具有最佳的信干噪比；当a(θ)与a(θi)有误差(失配)时，期望信号受到抑制，输出发生畸变，即信号自消(Self-canceling)现象，所以宽容性(稳健性)设计是自适应算法需要解决的问题.

1.2 宽容性Capon波束形成(RCB)

Li等[2]提出的宽容性Capon算法(Robust capon beam-forming, RCB)是在信号响应向量不确知的情况下，提供期望信号功率的宽容估计.实现方法是在导向向量的不确定性变化范围内，使期望信号的输出功率最大，因为导向向量误差将会使期望信号的输出功率减小.RCB算法可表述为一个模约束优化问题[2]，即

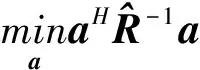
(4)

(5)

式中λ为Lagrange乘子.求L关于向量a的偏导数，并令其为0，可得满足代价函数最小的导向向量为

(6)

将式(5)代入式(4)的球面约束条件，并定义函数为

(7)

(8)

为了简化式(7)，定义临时向量[2]为

(9)

将式(9)代入式(7)，可得

(10)

式中zm为向量z的第m个元素.

显然式(10)是关于λ的单调递减函数，且有

所以只要确定了λ取值的上界和下界，就可用一元函数求根的方法唯一确定λ，从而根据式(6)可得满足式(4)的导向向量，使信号的输出功率最大，提高对导向向量误差的宽容性.根据式(10)，可确定λ的取值范围[2]为

(11)

(12)

可见，RCB算法也属于一种对角加载方法，只是通过导向向量的球体约束(或更一般地，椭球约束[2])，确定合适的加载量(1/λ).

2 概率约束宽容波束形成

上述RCB算法只需要作矩阵特征值分解和函数求根运算，而式(9)函数求根运算的计算量与特征值分解的计算量相比，可忽略不计.RCB算法的效率远高于SOCP[4]方法，而性能与SOCP方法相当，所以RCB方法具有工程可实现性.

RCB算法的主要问题是如何确定导向向量不确定性集合的大小，ε取得过大，虽然宽容性大，但损失了分辨力，ε过小，则宽容性不够.为了减弱失配最大情况下波束性能最优化方法[4]的过稳健性(Overly conservative[6])，文献[6]将文献[4]方法对不确定性集合内加权向量的约束条件，附加了概率约束.也就是当权向量的约束条件大于某个概率时，才寻求最优的权向量使代价函数最小[6].笔者研究概率约束的RCB算法，并减小RCB算法的过稳健性.

2.1 概率约束RCB算法

Pr{‖δ‖≤ε}≥p=1-pout

(13)

假设δ为均值为零、协方差为Cδ的复高斯向量，即

δ～N(0M,Cδ)

(14)

显然，若δi(i=1，2，…，M)服从高斯分布，则随机变量v服从χ2分布，其概率密度函数[7]为

pv(v)=[2M/2Γ(M/2)]-1vM/2-1exp(-v/2)

(15)

将式(15)代入式(14)，有

(16)

式中I为皮尔逊(Pearson)不完备Γ函数[7]，即

(17)

根据式(13，16)，可得

(18)

根据式(18)，就可用RCB算法得到宽容性波束权向量.

2.2 Lagrange乘子λ的确定

RCB算法对Lagrange乘子λ的求解是在导向向量不确定性集的边界上，即导向向量失配最大的情况，所以RCB算法具有过稳健性.为了减小过稳健性，对式(9)的求根采用二分法，在约束球体内寻求满足g(λ)≤0的λ的值，而不是局限在约束球面上精确地求取满足g(λ)=0的方程的根.具体实现步骤如下：

1) 设定迭代次数K和求根精度ξ.令K=0,判断g(λmin)和g(λmax)是否为0，若g(λmin)=0或g(λmax)=0，则λmin或λmax即为所求值，结束迭代求根过程，否则，令x1=λmin,x2=λmin.

由以上步骤可见：此方法是通过设定迭代次数和求根精度来控制算法的宽容性，因为利用该方法所求的宽容性导向向量式(6)可能落在不确定集的内部，而不仅仅在边界上，所以弱化了算法的过稳健性.

3 数值分析

考虑λ/2间距10元均匀线列阵，30°和50°方向存在两个干扰源，干噪比(干扰功率与背景噪声功率之比)均为20 dB.比较上述方法、RCB方法、LSMI方法(固定对角加载的SMI方法,Loaded SMI)和SMI方法4种算法.定义输出信干噪比[4]为

(19)

(20)

将式(20)代入式(19)，可得理想SINR为

(21)

3.1 导向向量无误差情况

图1 输出SINR与SNR的关系Fig.1 The relationship between output SINR and SNR

3.2 信号散射引起的导向向量误差情况

信号源经过传播介质到达接收阵，由于多途和散射效应，信号源往往不能看作理想的点源，而是空间分布源，例如水声信号，目标具有多个亮点，且水下传播介质具有不均匀性，造成接收信号的散布性，波阵面非理想的平面波.

考虑莱斯(Ricean)相干散射传播信道[4,6]，信号为中心角为θ0的空间散射源，导向向量的误差可建模[6]为

(22)

对于散射信道情况，输出信噪比表示为

(23)

(24)

式中PEV{·}为求主特征向量.式(24)代入式(23)，可得散射源的输出信噪比.

图2 输出SINR与SNR的关系Fig.2 The relationship between output SINR and SNR

当导向向量误差不确定集的大小ε均取1.2时，比较提出的算法和RCB算法的分辨性能，图3为SNR=-10 dB时的空间谱图，可见该算法的分辨力强于RCB方法，期望信号方向的功率输出大于RCB方法.利用该方法，在干扰方向的输出功率接近实际值(20 dB)，也即功率估计的偏差小于RCB方法.说明了2.2节提出的算法既能提高宽容性，又能保持较高的分辨力.

图3 空间谱图比较Fig.3 Comparison of spatial spectra

4 结 论

基于目标信号功率约束优化的宽容性Capon算法是一种宽容自适应波束形成的有效实现方案，但具有过稳健性.通过对导向向量误差施加概率约束，将误差约束集大小用波束损耗功率和导向向量误差的功率来描述，提供了一种误差约束集大小的经验设计方法.同时，提出了一种在导向向量误差约束集内部，对期望信号作最优功率估计的方法.理论和数值分析结果表明，宽容性波束形成既对导向向量误差具有宽容性，又有较高的分辨力，并提高了计算效率.

参考文献：

[1] COX H, ZESKIND R M, OWEN M H. Robust adaptive beamforming[J]. IEEE transacoustic, speech, signal processing,2015,35:1365-1376.

[2] LI J, STOICA P, WANG Z. On robust capon beamforming and diagonal loading[J]. IEEE transactions on signal processing,2013,51:1702-715.

[3] LORENZ R G，BOYD S P. Robust minimum variance beamforming[J]. IEEE transactions on signal processing,2015,53:1684-1696.

[4] VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J]. IEEE transations on signal processing,2013,51:313-324.

[5] MOREY A，PASQUAL I. Composition of new features into a wireless nurse call system[R]. Norwegians: University of Science and Technology，2014

[6] HE J, AO B Q. Control of hospital wireless calling system based on SCM[J]. Applied mechanics and materials,2013,336/337/338:52-55.

[7] GAO J Q, LIANG R H, WANG J. Research on the conjugate gradient algorithm with a modified incomplete cholesky preconditioner on GPU[J]. Journal of parallel and distributed computing,2014,74(2):2088-2098.

[8] MCDONOUGH R N, WHALEN A D. Detection of signals in noise[M]. 2th Ed. San Diego, California: Academic Press,2015.

[9] 彭宏，韩露莎.基于小波变换与多帧平均法融合的背景提取[J].浙江工业大学学报，2013，41(2)：228-231.

[10] 王卫红，张鹏灵.移动数据采集系统中拓扑规则的研究与实现[J].浙江工业大学学报，2017，45(1)：1-5.

[11] 金燕，王卫静.基于稀疏优化字典的图像去噪算法[J].浙江工业大学学报，2017，45(3)：320-324.