人工磁导体结构组成间隙波导的理论仿真研究
2018-05-08方超逯贵祯
方超,逯贵祯
(中国传媒大学 信息工程学院,北京 100024)
1 引言
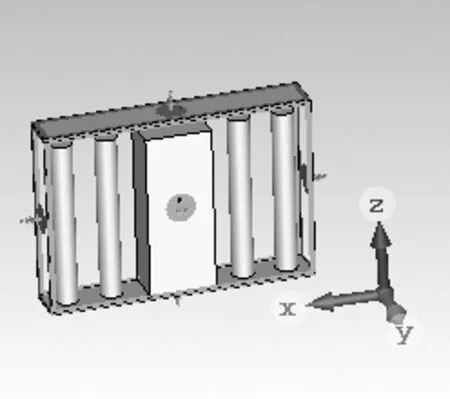
在毫米波传输技术的研究中,为了降低电磁波在传统波导中传播时的损耗,一种基于超材料人工磁导体结构的新型波导传输结构被提出。这种新型的波导传输结构如图1所示。
该结构的英文名字为“gap waveguide”,中文名字多称为“缝隙波导”,为了与“波导缝隙天线”区分,建议命名为“间隙波导”。
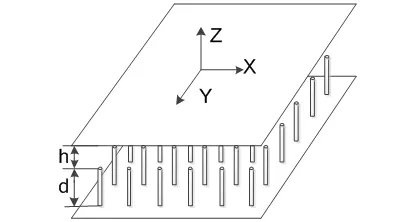
间隙波导的下层由两边的周期金属针床结构和中间的金属脊组成,间隙波导的上层是金属板。间隙波导的横截面示意图如图2所示。
电磁波被束缚在PEC-PEC(理想电导体)的区域中向前传播,而在PEC-HIS(高阻表面)区域中电磁波被抑制。与传统的矩形波导相比,间隙波导中传播的是TEM波,没有截止频率,并且由于少了侧面的两个金属表面,理论上间隙波导应该比传统金属矩形波导的传输损耗小。图2中形成HIS的周期金属针床结构又被称为AMC(人工磁导体),可以用来替代间隙波导理论模型中的PMC结构[1],当金属导体和人工磁导体表面间距小于1/4波长时,电磁波无法传播。

图2 间隙波导横截面示意图
国内对间隙波导结构的研究相对较少,国外研究间隙波导结构的主要有Chalmers University of Technology的Per-Simon Kildal教授团队。该团队在2009年提出了一种宽带,低损耗,能够传输TEM模式电磁波的间隙波导[2] [3],随后对间隙波导的研究主要集中在结构改进的方面。文献[4]提出了一种基于蘑菇形状周期结构的间隙波导,文献[5] [6]将金属针变成了弹簧和两个对接的到梯形,主要目的就是为了缩短金属针的长度,减小间隙波导的体积。文献[7]还在间隙波导结构的基础上提出了对应的谐振器结构。
2 平行周期金属线结构的色散方程
间隙波导传输线结构最核心、最基本的组成部分就是平行金属线组成的周期结构,如图3所示:
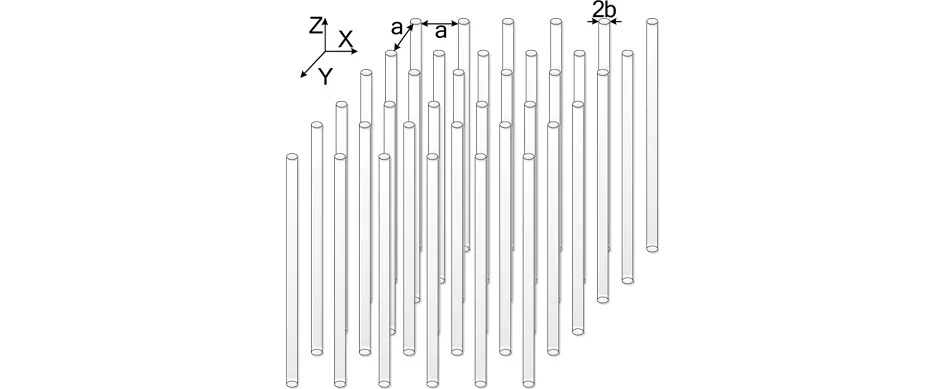
图3 平行周期金属线结构
这种结构在宏观上构成的媒质就属于电磁超材料的一种,也是最早被提出的一种电磁超材料形式。该结构在微波领域的应用有很多,例如天线的反射器、人工阻抗表面等。对于平行周期金属线结构的电磁特性理论研究有很多数值方法。但是在精确建模上进展甚微。基于传输线理论的方法只有在金属线间隔足够大的情况下才有准确结果[8],直到2002年,P.A.Belov提出了一种简便又能准确描述平行周期金属线结构色散特性的方法[9],并且给出了色散方程:
(1)
该色散方程在金属线半径远小于周期间隔尺寸和工作波长时非常准确。这个色散方程的数值结果表明电磁波在所有垂直于金属线表面的传播方向上都存在一个低频的禁带。当a≪π/k时,用泰勒级数展开和sin(x),色cos(x)散方程可以简化为:
(2)
其中,
(3)
公式2中的kp表示等离子频率对应的波数,更准确的说,它代表禁带的上边界。公式2可以类比于传统等离子频率的表达式,对于平行周期金属线结构该表达式更加准确,并且表明结果更依赖于平行周期金属线结构的物理尺寸。
3 人工磁导体中的传播模式
组成间隙波导传输线结构的第一步是将平行周期金属线固定在金属平板上形成人工磁导体结构(AMC),如图4所示:
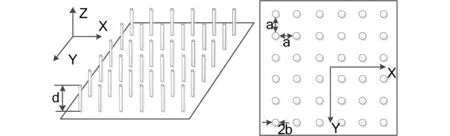
图4 人工磁导体结构
金属线高为d,半径为b,横向和纵向的周期间隔为a。则结构的介电常数为张量,可以用公式4表示:
(4)
其中,
(5)
而k代表主媒质中的波数,
(6)
kp是上一节提到的等离子体波数,只依赖于结构的尺寸,即周期间隔和金属丝半径。
在AMC结构中TM波的反射系数为:

(7)
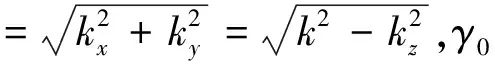
公式7中的反射系数是通过主媒质中TM波的衰减系数γTM来表示的,当平行金属线足够密集时,即当a/b≪1,b/a为常数时,γTM→kp→1/a→∞。kz是由平面波的入射方向决定的。对于TE波,反射系数只和平面金属板有关,因为TE波垂直于金属线,所以平行金属线结构对TE波没有影响,则TE波的反射系数为:
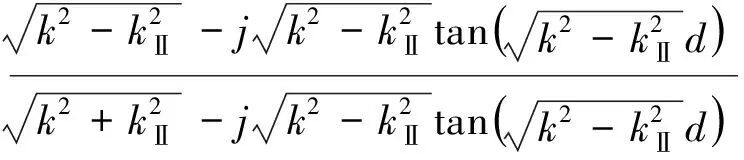
(8)
当金属线足够密集时,

(9)
当只考虑TEM模式时,反射系数也可以用公式9来表示。
因此,当平行金属线足够密集时,媒质为各项异性材料,εxx=εyy=1,εzz=∞,媒质的等效阻抗为:
Zs=jξtan(kd)
(10)
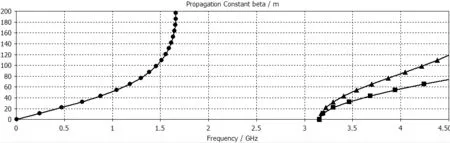
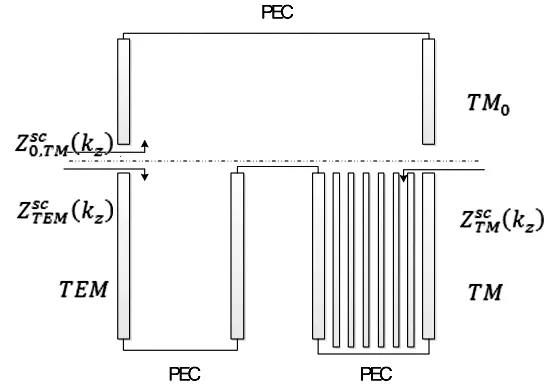
当d≤λ/4时,媒质的阻抗为感性;当λ/4 在上一节所介绍的人工磁导体上间隔一段距离覆盖与之平行的金属板如图5: 图5 AMC-PEC结构 金属线的高度为d,周期金属柱的上方覆盖金属板,与金属柱结构相距h。覆盖金属板后的形成的AMC-PEC结构中的场分布比没有覆盖金属板的结构要更加复杂,电磁波在限定空间内传播特性也可以用ΓTM(kz)和ΓTE(kz)来描述。由结构可知,上边界为PEC,切向电场为0,即: [ejkzz+ΓTM,TE(kz)e-jkzz]z=h=0 (11) 对于TE波而言,波的传播模式只取决于上下金属板,即上下两个PEC边界条件,故: kz=π/(h+d) (12) 对于TM波而言,由公式7和11可得: (13) 将公式13类比于电路谐振方程: (14) 由此可以得出AMC-PEC结构的等效电路图如图6所示[10]: 图6 AMC-PEC结构等效电路图 (15) 即: (16) 其中虚线表示TM模式的波,实线表示TE模式的波,结果都能够看出在1.2GHz-2.3GHz有一个明显的禁带,表明这个频段内的电磁波不能在该结构中传播,给利用AMC-PEC结构制作间隙波导提供了理论基础。 图7 AMC-PEC结构色散曲线 首先对AMC-PEC结构的色散曲线进行仿真,建立如图8所示的一个周期结构,h=5mm,a=8mm,b=4mm: 图8 AMC-PEC结构单个周期仿真模型 可以得到AMC-PEC结构的色散曲线。 由图9-图11可以看出d取不同的值,直接影响禁带的带宽,而且禁带的下限满足d=λ/4的关系。当h=60mm时,仿真结果和数值计算结果匹配得很好。 然后,对间隙波导结构的散射曲线进行仿真,可以利用周期结构仿真模块对如图12所示的一个周期进行仿真,参数设为h=5mm,d=60mm,a=8mm,b=4mm: 得到色散曲线如图13所示。 可以看出在AMC-PEC结构1.2-2.2GHz的禁带中出现了一个新的传播模式,是间隙波导中的准TEM波。 最后,为了证明间隙波导的可行性,分别用了CST和HFSS对间隙波导的S参数和电磁场分布进行了仿真,得到的结果如图14-16所示。 图9 d=40mm时 图10 d=60mm时 图11 d=80mm时 图12 间隙波导单个周期仿真模型 图13 间隙波导色散曲线 图14 CST仿真S参数(实线S11、虚线S21) 图15 HFSS仿真S参数(实线S11、虚线S21) 图16 电场分布示意图 图14和图15分别用HFSS和CST对间隙波导的S参数进行了仿真,可以看出两个结果在1G-3G频段有相同的趋势,S11和S21满足波导传输的要求,两种软件的结果相互验证,证明了间隙波导的可行性。需要强调的是,由于CST采用的是时域的方法,能够迅速得到结果,而用HFSS仿真的过程则非常缓慢。图16是间隙波导的电场分布示意图,可以明显看出间隙波导中的电场被束缚在中间的脊区域,这也和理论相符。 [1]逯贵祯,洪楚雨,方超.金属条带缝隙波导结构特性研究[J].微波学报,2014(2):184-186. [2]Kildal P S,et al.Wideband,Low loss,Low-cost,Quasi-TEM Metamaterial-based Local Waveguides in Air Gaps Between Parallel Metal Plates[C].International Conference on Electromagnetics in Advanced Applications,Torino,Italy,2009:588-591. [3]Kildal P S,et al.Local Metamaterial Based Waveguides in Gaps Between Parallel Metal Plates[J].IEEE Antennas and Wireless Propagation Letters,2009,8(4):84-87. [4]Pucci E,Kildal P S,et al.New Microstrip Gap Waveguide on Mushroom Type EBG for Packaging of Microwave Components[J].IEEE Microwave and Wireless Components Letters,2012,22(3):129-131. [5]Iglesias E R,Kildal P S,et al.Bed of Springs for Packaging of Microstrip Circuits in the Microwave Frequency Range[J].IEEE Transactions on Components,Packaging and Manufacturing Technology,2012,2(10):1623- 1628. [6]Shams S I,Kishk A A,et al.Double Cone Ultra Wide band Unit Cell in Ridge Gap Waveguides[C].Antennas & Propagation Society International Symposium,Memphis,Tennessee,USA,2014:1768- 1769. [7]Pucci E,Zaman A U,et al.Study of Q-factors of ridge and groove gap waveguide resonators[J].IET Microwaves,Antennas& Propagation,2013,7(11):900-908. [8]Nicorovichi N A,McPhedran R C,et al,Photonic band gaps for arrays of perfectly conducting cylinders[J].Physical Review E,1995,52(1):1135-1145. [9]Belov P A,Marques R,et al.Strong spatial dispersion in wire media in the very large wavelength limit[J].Physical Review B,2003,67(11):621-623. [10]Polemi A,Maci S,et al.Dispersion Characteristics of a Metamaterial-Based Parallel-Plate Ridge Gap Waveguide Realized by Bed of Nails[J].IEEE Transactions on Antennas and Propagation,2011,59(3):904- 913.4 AMC-PEC结构的色散分析



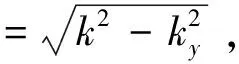

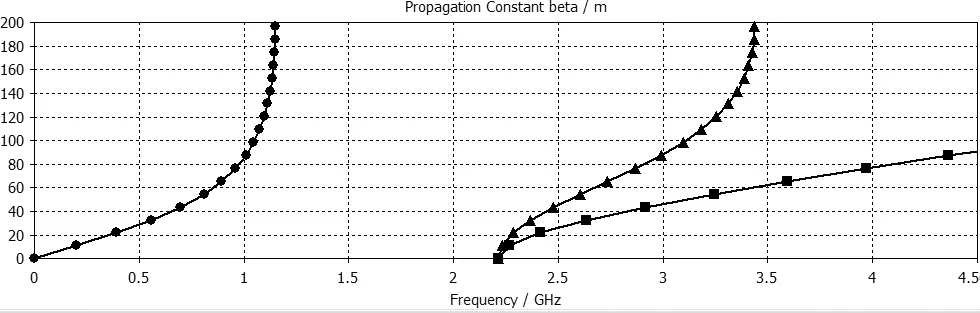
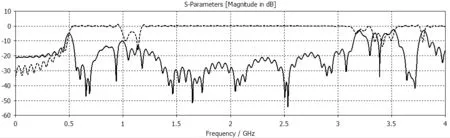
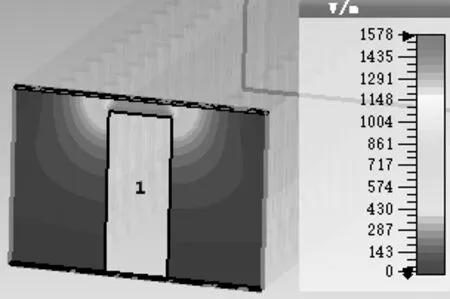
5 间隙波导结构的仿真分析