动能拦截器姿控地面验证试验误差建模与仿真
2018-05-08臧月进李仁俊周藜莎
臧月进,李仁俊,周藜莎
(上海机电工程研究所, 上海 201109)
为实现空间拦截器的最佳机动效果并时刻将目标锁定在导引头视场内[1],需对拦截器进行姿态稳定控制,使拦截器三轴稳定并稳定跟踪目标视线的变化[2-3]。姿控地面试验主要为验证拦截器姿控系统的响应快速性和控制精度,为固定姿控样机的位置,在样机的质心位置悬挂吊绳实现样机的绕质心转动。
文献[4]重点对动力系统响应延迟进行了建模与仿真,而文献[5]忽略了燃料消耗引起质心漂移带来的干扰力矩影响,未对误差进行全面系统建模。本文以拦截器的姿控地面验证试验为背景,集中考虑了姿控系统存在的各类误差源,全面系统建立拦截器误差数学模型,并进行仿真验证。
1 惯组误差模型
由于姿控验证试验主要验证姿态稳定回路,不需要加速度计信息,因此惯组误差主要考虑陀螺初始安装角误差。由于3个方向上的陀螺在安装时每个坐标轴都有一定的误差角,故定以安装误差角为θsi、ψsi(i=1~3)。假定3个陀螺实际敏感到的分量为ωsx、ωsy、ωsz,分别偏离对应的坐标轴,用高低角θsi和ψsi衡量。设ωx、ωy、ωz为弹体系三个轴上的真实角速度分量,则有:
转换矩阵Bs为
因此有
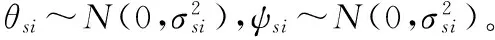
2 动力系统误差模型
动力系统误差指姿控发动机的推力误差[6]以及因发动机燃料消耗引起的质心变化。
2.1 发动机误差模型
动力系统误差主要是指姿控发动机的推力大小误差和推力偏斜误差[7]:
1) 姿控推力误差
发动机的实际推力大小的计算表示为
其中,Fin为发动机名义推力,FiA为姿控发动机实际推力(i=1~4)。
2) 姿控推力偏心误差
以3#发动机为例,定义姿控发动机实际推力偏斜误差角θdi、ψdi(i=1~4)。
如图1姿控发动机布局示意,以#3姿控发动机为例,其推力在弹体系中的分量表示为
其中θd3定义为#3喷管推力中心与拦截器理论上的剖平面YOZ面的夹角,ψd3定义为#3喷管推力在拦截器理论上剖平面YOZ面内投影与Y轴的夹角,如图2所示。
其余姿控发动机的推力分量可以类似推导如下:
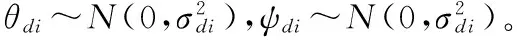
2.2 质心漂移模型
实际操作中很难保证悬挂点正好是样机质心位置,同时随着样机燃料的消耗,样机的质心也在移动。质心漂移误差包括静态漂移和动态漂移,分为径向和轴向两个方向。
设质心轴向静态漂移lAx0,径向漂移lRy0、lRz0。静态漂移可以通过结构模型一次计算出,而后固定不变[8]。动态漂移则按正态分布不断变化,所以质心漂移的计算公式为
lAx、lRy、lRz为实际样机的质心漂移量。
拦截器的质心漂移对姿控发动机产生影响,可得存在质心漂移误差时的姿控力矩:
其中:MA为姿控力矩,R为拦截器姿控截面半径,l为姿控力臂。
3 吊摆干扰模型
在姿控发动机的激励下,受迫运动如图3所示,拦截器样机会产生沿吊绳切向的附加单摆干扰运动。
在吊绳坐标系oxlylzl下,运动学、动力学模型如下:
运动学模型:
动力学模型:
即
则单摆模型为
其中,l为吊绳长度,m为样机质量,δ为样机吊绳的摆偏角,ω为样机的摆动角速度。
在弹体坐标系中,由吊绳引起的干扰力矩如下:
其中lAx为样机在ObXb轴上的质心偏移量。
4 仿真分析
假设某拦截器的满载质量20.0 kg,空载质量19.50 kg,长0.60 m,偏航通道转动惯量为0.50 kg·m2,偏航通道喷管力臂为0.30 m,姿控发动机额定推力为20.0 N。
考虑各类误差如表1所示。
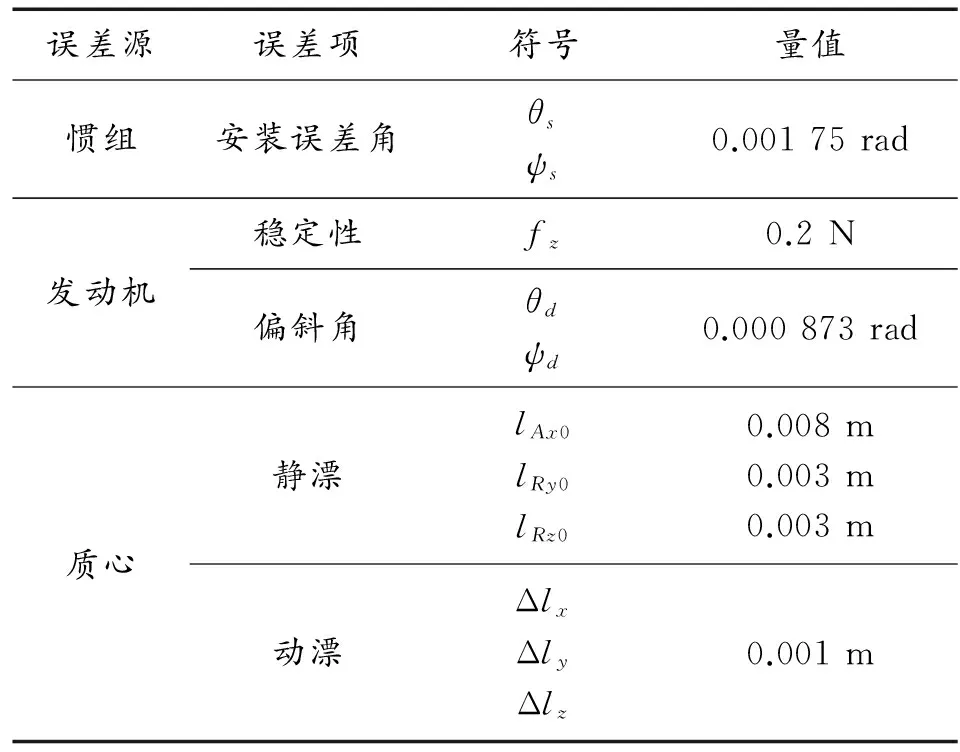
表1 姿控系统误差一览表
综合考虑上述误差,以偏航通道为例,对应的姿态和角速率如图4和图5所示。样机可在0.15 s内响应初始5°的偏角,稳态精度为0.1°,最大角速率60 (°)/s,姿态指向稳定性为1 (°)/s。
从表2蒙特卡洛打靶的误差统计可见,对姿态指向精度影响起主要作用的是推力的稳定性和样机的质心漂移。
图6为引起上述姿态偏转的偏航通道控制力,其中推力考虑了10%的稳定性误差。
从图7可见,由于吊绳的影响,样机在侧向喷管的激励下周期性摆动,尤其第一个持续100 ms的脉冲下引起最大摆角0.1°,样机摆幅0.01 m。

表2 带各类误差的蒙特卡洛打靶精度统计
从上述单偏航通道误差模型的仿真可见,样机消耗的燃料也随误差模型的差别有所差异,其中质心的漂移和推力的稳定性对姿态的精度影响最大,但稳定控制系统仍能满足精度要求。
5 结论
本文针对姿控地面验证,重点建立了测量环节和执行环节的各类误差模型,尤其对悬吊这一特殊场景下建立了受迫单摆模型,并进行了仿真,结果验证了该误差模型的合理性。当然实际飞行控制中,姿轨控耦合误差、惯组测量的阈值误差以及控制指令延时等等还需要进一步深入研究。
参考文献:
[1] 郭清晨,杨宝庆,米双山.基于PWPF的动能拦截器姿态控制方法研究[J].探测与控制学报,2008,30(b10):116-119.
[2] 汤国建,任萱,吴瑞林.一种用于快速跟踪视线的空间拦截器姿态控制方法[J].航天控制,2000,18(2):52-10.
[3] 王清,杨宝庆,马克茂.一种优化PWPF调节器在动能拦截器末制导中的应用研究[J].宇航学报,2005,26(5):576-580.
[4] 臧月进,曾亮,李仁俊.基于数字变力矩的拦截器脉冲姿态控制律设计[J].兵工自动化,2017(7):54-58.
[5] 程凤舟,万自明,陈士橹.大气层外动能拦截器末制导分析[J].飞行力学,2002,20(1):38-41.
[6] 郭庆,杨明,王子才.拦截器末制导段误差模型的建立与仿真[J].计算机仿真,2007,24(3):58-61.
[7] 刘庆鸿,陈德源,王子才.动能拦截器拦截战术弹道导弹的脱靶量分析[J].系统仿真学报,2002,14(2):200-203.
[8] 高大远,陈克俊,胡德文.动能拦截器末制导控制系统建模与仿真[J].宇航学报,2005,26(4):420-424.
