让数学思想方法在解题中闪光

■吴燕凤

数学思想方法是数学解题的精髓,属于思维的范畴,同学们要能够领会并学会运用。掌握数学思想方法,对于数学解题大有益处。

一、函数与方程思想

例1 求函数y=cos2x+sinx(|x |≤)的最大值与最小值。

评析:在解答此类试题时,要能够建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。

二、数形结合思想

例 2 函数f(x)=Asin(ωx+φ)(A＞0,ω＞0,|φ|＜)的部分图像如图1所示,若 x1,x2∈ (-),且f(x1)=f(x2),则f(x1+x2)=( )。

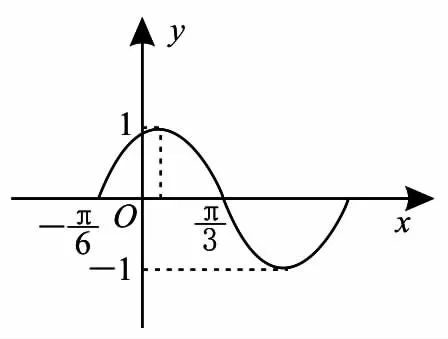
图1

三、分类讨论思想

例 3 已知函数y=-sin2x+asinx-的最大值为2,则a的值为____。

评析:分类讨论的基本思路是将一个较复杂的数学问题分解(或分割)成若干个基础性问题,通过对基础性问题的解答来实现对原问题的解决。本题中sinx∈[-1,1],需要分三种情况讨论求解,即

四、等价与转化思想

解:(法1)利用“切化弦”求解。

因为tanα=2,所以sinα=2cosα。又

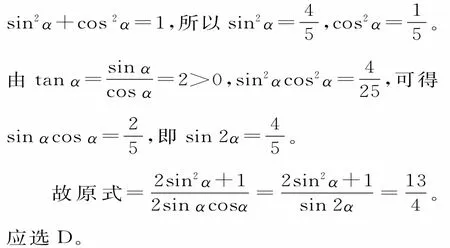
(法2)利用“弦化切”求解。

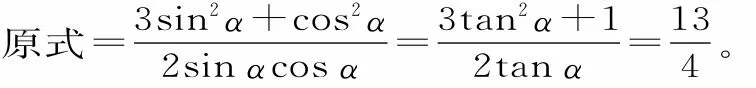
例 5 已知tanα=2,求下列各式的值。

(3)4sin2α-3sinαcosα-5cos2α。

解:(1)注意所求式的分子、分母均为关于sinα,cosα的一次齐次式,可将分子、分母同除以cosα(cosα≠0),然后代入tanα=2即可。原式

(2)所求式的分子、分母同除以cos2α(cosα≠0),可得原式

(3)注意到所求式为sinα,cosα的二次齐次式,不妨把其看成分式,将分母变为sin2α+cos2α,即可顺利求解。

评析:转化与化归的思想方法,就是在研究和解决有关数学问题时,采用某种手段将问题通过变换使之转化,进而得到解决问题的一种方法。利用sin2α+cos2α=1可以实现角α的正余弦互化,利用=tanα可以实现角α的弦切互化。