广义模糊粗糙集模型中的矩阵运算

梁 美 社

(石家庄职业技术学院 科技发展与校企合作部，河北 石家庄 050081)

Pawlak于1982年首次提出了粗糙集理论,主要用来处理不精确、不确定、不完全的数据系统[1].随后,该理论被广泛应用于人工智能的各个领域[2].在Pawlak粗糙集模型中,等价关系起着至关重要的作用,由于这一关系过于苛刻,因此在很大程度上限制了该近似算子在粗糙集模型中的应用.近年来, 许多学者对粗糙集进行了各种推广研究[3-9],例如基于邻域关系、相似关系、一般二元关系等的研究.文献[10]从公理化角度研究了广义模糊粗糙集及其近似算子.文献[11]在文献[10]的基础上，提出了基于模糊关系的广义模糊粗糙集的(α,β)上下近似算子.

矩阵最早来自于方程组的系数及常数所构成的二维数据表格.矩阵算子用于建立从当前矩阵到特殊类型矩阵的映射.文献[2-20]分别从不同角度研究了矩阵算子在经典粗糙集模型和变精度粗糙集模型中的应用.文献[21]用矩阵方法研究了双论域粗糙集,提出了双论域上的关系矩阵，并构造了两个布尔方阵.文献[22]基于等价关系矩阵和子集列矩阵,研究了模糊粗糙集模型,取得了不错的结果.这些都是利用论域上的等价关系矩阵来计算上下近似。本文在文献[11]的基础上,利用截关系矩阵、模糊子集的截列阵之间的运算来表示广义模糊粗糙集的上下近似算子,并进一步计算广义模糊粗糙集的粗糙度和相似度.

1 预备知识

1.1 广义模糊粗糙集

设U为一个非空有限论域,P(U)为U上的所有子集构成的集合,F(U)为U上所有模糊子集构成的集合.对于任意A∈F(U)，∀α∈[0,1],Aα={x∈U;A(x)≥α}和Aα+={x∈U;A(x)>α}分别为模糊子集A的α-水平截集和α-水平强截集.由∀A,B∈F(U)知，(A∪B)α=Aα∪Bα,(A∩B)α=Aα∩Bα.

定理1设(U,R)为广义模糊近似空间,对于任意A∈F(U),若0.5<β≤1，则

性质1设(U,R)为广义模糊近似空间.对于∀A,B∈F(U)有：

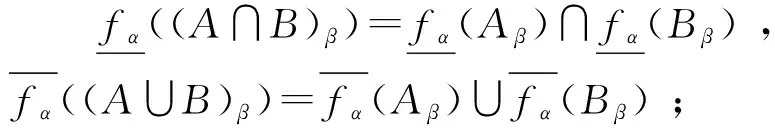
(4)A,B∈F(U),若A⊆B则：

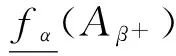
以上性质均可根据定义1及定理1直接证明.

由定义1、定理1知,通过截关系，可将模糊信息系统转化为经典信息系统,通过研究转化后的经典信息系统的性质，来间接反映原模糊信息系统的相关性质.

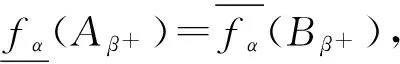
1.2 广义模糊粗糙集的(α,β)粗糙度、相似性度量

由定理1得到了一对对偶的上下近似算子,由这对对偶算子可以定义U上任意模糊子集的粗糙度.

结合文献[23],也可以得到U上任意两个模糊子集的相似性.

定义4设(U,R)为广义模糊近似空间,∀A,B∈F(U),ϖ1,ϖ2∈[0,1],ϖ1+ϖ2=1,定义A,B在近似空间(U,R)中关于参数(α,β)的相似性度量为：

2 广义模糊粗糙集模型中的矩阵运算

2.1 (α,β)上下近似的矩阵表示

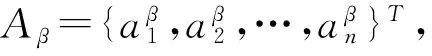
证明(1)证明下近似的情形

(2)证明上近似的情形

2.2 广义模糊粗糙集的(α,β)粗糙度、相似性度量的矩阵计算

根据定义3,A∈F(U),定义A在近似空间(U,R)中关于参数(α,β)的粗糙度的计算可以用矩阵计算，表示为：

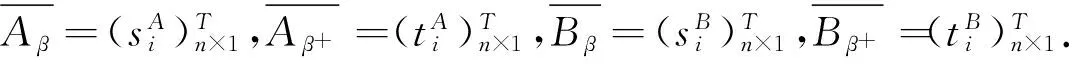
2.3 实例分析

设论域U={x1,x2,…,x5},R为U上的模糊关系,取α=0.8,β=0.4,A,B∈F(U),

A=[0.1,0.7,0.5,0.9,0.2]T，

B=[0.5，0.3,0.8,0.2,0.9]T.

R截关系矩阵、模糊子集A,B的截列阵分别为：

A0.4=[0,1,1,1,0]T,B0.4=[1,0,1,0,1]T.

根据定理2,模糊子集A,B在近似空间(U,R)中关于参数(0.8,0.4)的上下近似矩阵分别为：

模糊子集A,B在近似空间(U,R)中关于参数(0.8,0.4)的上下近似为：

A,B在近似空间(U,R)中关于参数(0.8,0.4)的粗糙度为：

令ϖ1=0.4,ϖ2=0.6,A,B在近似空间(U,R)中关于参数(0.8,0.4)的相似度为：

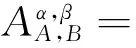
3 结语

本文首先利用截关系,将模糊信息系统转化为经典信息系统,而后将矩阵思想应用于该系统中.研究表明,用矩阵运算计算参数(α,β)下模糊子集的上下近似、粗糙度及相似度简单易行.根据实际问题需要，可以选取不同的参数(α,β)，以得到不同的结果.

参考文献：

[1] PAWLAK Z.Rough Set[J].International Journal of Computer and Information Sciences,1982,11(5):205-218.

[2] 张文修,梁怡,吴伟志，等.信息系统与知识发现[M].北京:科学出版社,2003:1-228.

[3] ZIARKO W.Variable Precision Rough Set Model[J].Journal of Computer and System Sciences,1993,46(1):39-59.

[4] INUIGUCHI M,YOSHIOKA Y,KUSUNOKI Y.Variable-precision Dominance-based Rough Set Approach and Attribute Reduction[J].International Journal of Approximate Reasoning,2009,50(8):1199-1214.

[5] LIU GUILONG.Generalized Rough Sets over Fuzzy Lattices[J].Information Sciences,2008,178 (6):1651-1662.

[6] RADZIKOWSKA A,KERRE E.Fuzzy Rough Sets Based on Residuated Lattices[M].Berlin:Heidelberg Springer,2005:278-296.

[7] 石梦婷,刘文奇,范敏.两个域上的覆盖粗糙集模型[J]. 计算机工程与应用,2013,49(10):132-135.

[8] LIU GUILONG.Rough Set Theory Based on two Universal Sets and Its Applications[J].Knowledge-Based Systems,2010,23(2):110-115.

[9] YAO YIYU.Generalized Rough Set Models[J].Rough Sets in Knowledge Discovery,1998(1):286-318.

[10] MADZIKOWSKA A M,KERRE E E.A Comparative Study of Fuzzy Rough Sets[J].Fuzzy Set and Systems,2002,126(2):137-155.

[11] 吴建春,李晓琴.广义模糊粗糙集的粗糙度[J].兰州理工大学学报,2014,40(6):156-159.

[12] GUAN J W,BELL D A,GUAN Z.Matrix Computation for Information Systems[J].Information Sciences,2001,131(1):129-156.

[13] 雷晓蔚.粗糙集理论的矩阵方法[J].计算机工程与应用,2006,42(17):73-75.

[14] 杨勇.粗糙集的矩阵定义[J].计算机工程与应用,2007,43(14):1-2.

[15] 罗来鹏.粗糙集的矩阵关系[J].数学的实践与认识,2009(23):203-207.

[16] 罗来鹏,刘二根,曾毅.粗糙集理论研究的矩阵方法[J].系统工程与电子技术,2009(4):859-862.

[17] ZHANG J B,LI T R,RUAN D,et al.Rough Sets Based Matrix Approaches with Dynamic Attribute Variation in Set-valuedtion Systems[J].International Journal of Approximaximate Reasoning,2012,53(4):620-635.

[18] LIU GUILONG.The Axiomatization of Rough Set Upper Approximation Operation[J].Fundamental Informaticae,2006,69(3):331-342.

[19] 王磊.信息系统动态知识更新的矩阵方法研究[D].成都:西南交通大学,2013.

[20] 王磊,李天瑞.基于矩阵的粗糙集上下近似的计算方法[J].模式识别与人工智能,2011,24(6):756-762.

[21] 刘慧,祝峰,林姿琼.双论域粗糙集的矩阵表示[J].计算机工程与应用,2015,(24):154-158.

[22] 李中然,舒兰.模糊粗糙集的上下近似的矩阵计算[J].计算机技术与发展,2015,25(4):10-12.

[23] 林娟,米据生,解滨.粗糙集的两种相似性度量[J].计算机科学,2015,42(6):97-100.