CoKriging插值法理论与实验教学
2018-05-07刘祖涵王莉莉詹新武张红梅王文丰
刘祖涵, 王莉莉, 詹新武, 张红梅, 王文丰
(南昌工程学院 a.信息工程学院;b.理学院;c.水利与生态工程学院,江西 南昌 330099)
目前,地理统计技术已被广泛地应用于空间数据分析中,涉及煤炭行业、地质、生物学、矿业、气象、水文、土壤、环境、生态和流行病学等领域[1-8].地理统计技术发展之初的主要目的是,在某一区域内,以少数的样本数据,依据数据的空间变异结构,估算出完整的空间分布情况.联合克利金法(CoKriging插值法)能以不同的统计结构,利用样本数较为充足的辅助随机变数来推估取样点较少的气候水文资料,进而获得较为准确的因子变化特征的空间分布情况.同一空间位置样点的多个属性之间的某个属性的空间分布与其他属性(例如气象台站的经度、纬度、海拔等)密切相关,且某些属性不易获得,而另一些属性则易于获取.如果两种属性空间相关,可以考虑选用联合克利金法,把区域化变量的最佳估值方法从单一属性发展到两个以上的协同区域化属性,但它在计算中要用到两种属性各自的半方差函数和交叉半方差函数,比较复杂,学生不易理解和掌握.为此,笔者在地理信息系统上机理论与实验教学过程中,在全面分析地统计学基本原理的基础上,设计了地统计学的CoKriging法,以塔里木河流域日平均降水的 Hurst指数H1与其他属性(包括流域23个气象台站的经度、纬度、海拔)为实验数据,在ArcGIS 10.2 软件平台,对指数H1进行了联合克利金法的空间插值.
1 区域化变量理论
一事物若能以特定统计空间结构表示,则称为区域化(Regionalized).若Z(x)定义为位置x的随机量测值,则Z(x)称为区域化变量(Regionalized variable)[9],自然界的空间变量,如矿产分布、地形高程分布及降雨分布,均可视为区域化变量.区域化变量具有两个特性,局部而言,点与点间呈不规则变化,可视为随机变数;整体而言,可用某种统计结构来代表其平均结构[10].
随机变数Z(x)与Z(x+h)随着距离的增大而相关性降低,因此共变异数函数cov(h)也随距离的增大而逐渐变小.通常相距很远的Z(x)与Z(x+h)之间的空间相依性为0,若h大于某特定距离,Z(x)与Z(x+h)的相关性趋近于0,则此特定距离称为影响范围(Range),可以代表相关性有无的分界距离.区域性变数的空间结构可用半变异图(Semivariogram)表示.半变异数是一种表现区域化变量沿某一特定方向的不同位置变化率的值.一般常用实验半变异图(Experimental semivariogram)来进行空间结构性分析.
1.1 半变异图理论
假设区域化变量符合定常性(Stationary),即其平均值为一常数.沿某方向任取两点样本配对,两点间的距离为h个单位,
则定义半变异数为:
(1)
其中,Z(xi)为第i点的区域变数值;Z(xi+h)为第i点相距h个间隔的区域变数值;Nh为取样点的配对数.
在实践中,样本的长度是有限的.把有限实测样本值构成的变异函数称为实验,根据不同的h值及所对应的γ(h)值可以绘出半变异图.相距愈小的两点,其半变异数愈小.随着距离的增加,任意两点间的空间相依性愈小,区域变数中的半变异数趋向一个稳定的值,此稳定值称为总体半变异数(Sill),而总体半变异数的最小h值称为影响范围(Range),如图1(a)所示.
理论上,当h=0 时,γ(0)应该为0.但实际应用中,常会出现当h趋近于0 时,γ(0)的值呈现不连续情况,以数学式表示为:
(2)
这种当距离趋近于0时半变异图的不连续性,称为块金效应(Nugget effect)[11],如图1(b)所示,代表距离小于采样间距内的变异性以及测量误差.
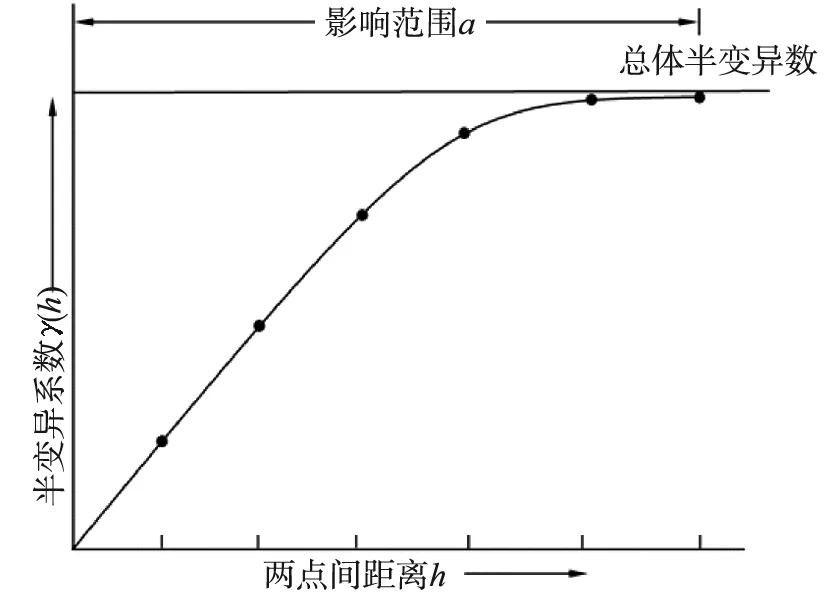
(a) 理想情况
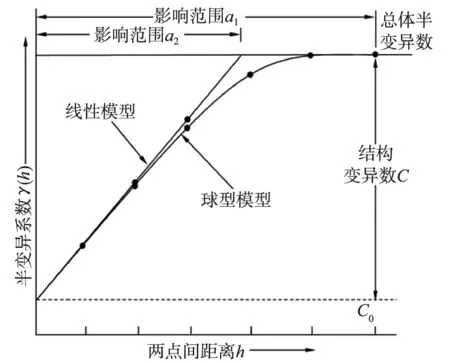
(b)有块金效应的情况
1.2 常用的半变异图模型
由于一般绘制的实验半变异图常呈现散乱的不规则点,无法发现一个较佳的趋势以求出最佳的Range和Sill值,因此,常假设某一函数模型为实验半变异图的方程式,利用试误法求出最佳拟合曲线,再由曲线求出相对应的半变异数及其影响范围.
变异函数表征了在联合克利金法插值中权值取决于变量的空间结构[12],一般用变异曲线表示,常用的有球状模型、高斯模型及指数模型.
(1)球形模型(Spherical model)
(3)
Sill=C0+C1, Range=a.
(2)指数模型(Exponential model)
(4)
Sill=C0+C1, Range=3a.
(3)高斯模型(Gaussian model)
(5)
(4)幂级数模型(Power model)
γ(h)=C0+C1hθθ<2,
(6)
no Sill,no Range.
2 联合克利金法
联合克利金法(CoKriging)的主要原理为,将两个或两个以上具有高度空间相关性的区域化随机变数合并考虑,进行空间资料推估[13].分析过程大致与一般克利金法(Kriging)相似,着眼点在于利用取样点较多的资料辅助推估取样点较少的资料,降低其推估误差,常用于主要变数取样点较少时,使用与主要变数高度相关,且取样点较多的次要变数的辅助推估.需符合三个条件.
(1)线性
估计值为观测值的线性组合.
(7)
(2)不偏估
估计值的期望值等于观测值的期望值.
(8)
将(7)式代入(8)式可得:
(9)
(3)优化
估计值与观测值差的变异数为最小,即
(10)
将(7)式代入(10)式,利用拉格朗日法引入拉格朗日参数μ1和μ2,则拉格朗日函数L为:

(11)

(12)
写成矩阵形式为:

(13)


(14)
估计误差(Estimation error)为:
(15)
文献[15]利用高斯模型成功地分析了乌鲁木齐河流域月平均降水数据的分布规律,并给该模型的参数赋予了明确的物理意义,认为该模型不仅能够实现降水在时间和空间上的插值,而且能够实现降水量和降水分布函数的相互转换,因此本文用高斯模型对文献[1]中的塔里木河流域51年的日降水量的Hurst指数H1进行联合克利金插值.需要指出的是,Hurst指数H1一般介于0到1之间,它反映的是非线性时间序列统计特征量的标度不变性和表征序列的长记忆性.
3 实验过程及结果
在地理信息系统实验课上,以ArcGIS 10.2软件为平台,对塔里木河流域51年日降水量的Hurst指数H1进行CoKriging空间插值举例说明.
第一步,点击地统计向导.
ArcGIS的地统计分析有一个地统计向导,按照这个向导一步一步就可以实现CoKriging空间插值.点击向导,截图如图2所示.
第二步,选择输入的数据和属性,采用CoKriging方法选择插值模型,如图3所示,然后点Next按钮即可.

图2地统计向导截图

图3 选择插值模型截图
第三步,选择插值的主要变量(降水量)及三个次要变量(23个气象台站的经度、纬度及海拔高度),然后点击Next按钮,如图4所示.
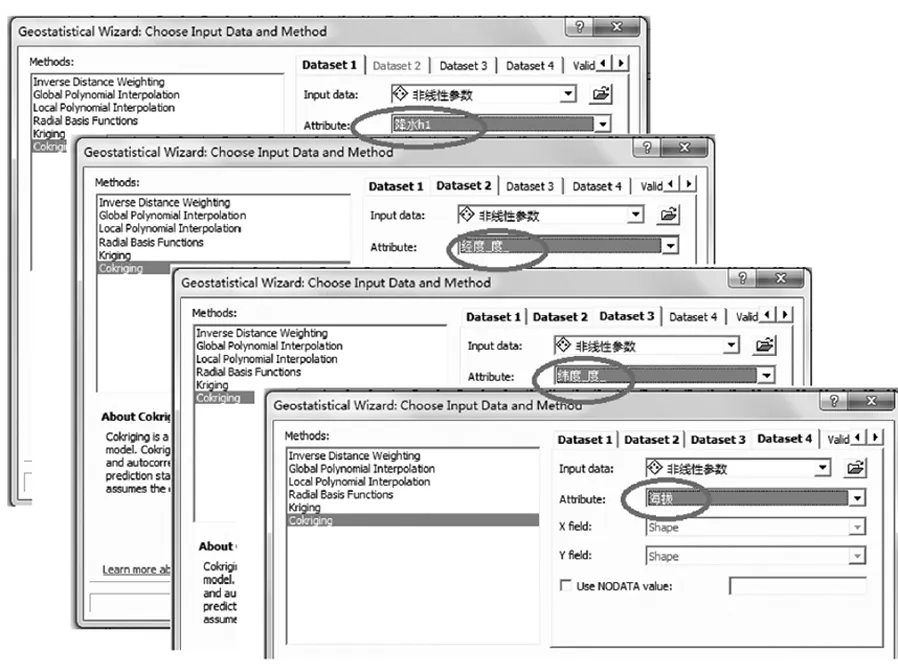
图4选择插值的主要变量截图
第四步,确定高斯模型.
这一步对插值的精度影响很大.根据左上角的高斯函数云图,在右边模型栏内,选择对其拟合较好的模型.通过调整搜寻角度和搜寻半径,确定一个合适的模型,该模型的参数在左下角框内给出,如图5所示,然后点击Next按钮.同样,可以选择默认设置.
第五步,搜寻邻居的调整.
选择默认设置,截图如图6所示.

图5 确定高斯模型的截图

图6 搜寻邻居的调整截图
第六步,交叉验证结果.
这一步给出了上述设置计算结果的交叉验证值,通过它可以分析各种验证的精度.如果误差很大,不能通过检验,则需要重新设置,如图7所示.

图7获得交叉验证结果截图
点击Finish按钮,会得到这个过程的一个总结,如图8所示.例如数据预处理过程、采用的模型等.
得到插值的结果如图9所示.

图8 过程总结截图
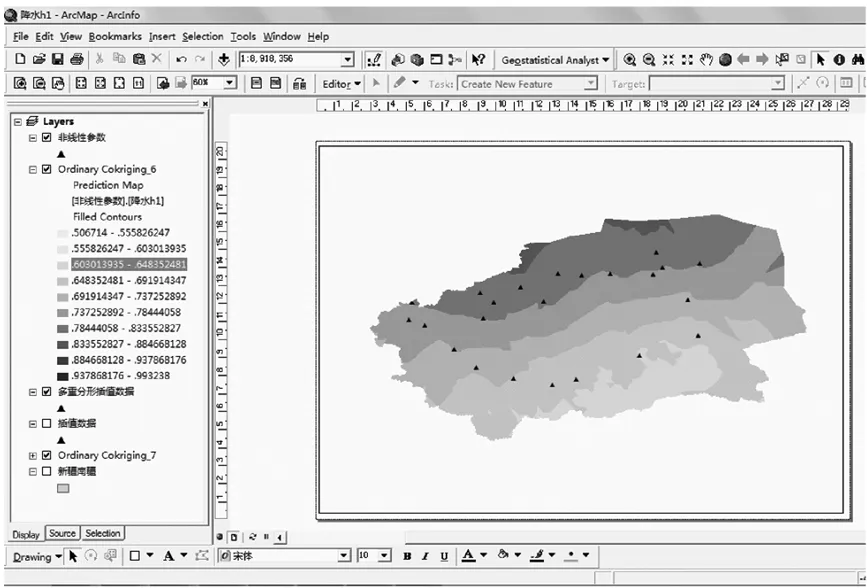
图9 插值结果截图
结果表明,联合克利金法可以精确显示塔里木河流域的降水变化的长记忆性空间分布规律.这种方法有利于学生在上机实验过程中理解和掌握相关知识,明确在实际的工程项目中,研究要素不仅受大尺度因素的制约,而且还受小尺度因素的影响,具有空间分布的不确定性.
参考文献:
[1] 刘祖涵.塔里木河流域气候——水文过程的复杂性与非线性研究[D].上海:华东师范大学,2014.
[2] HENGL T,MINASNY B,GOULD M.A Geostatistical Analysis of Geostatistics[J].Scientometrics,2009,80(2):491-514.
[3] SRIVASTAVA RM.Geostatistics:A Toolkit for Data Analysis,Apatial Prediction and Risk Management in the Coal Industry[J].International Journal of Coal Geology,2013,112(2):2-13.
[4] ASSARI A,MOHAMMADI Z.Combined Use of Geostatistics and Multi-criteria Decision Analysis to Determine New Pumping Well Locations in the Gol-gohar Open Pit Mine,Iran[J].Mine Water & the Environment,2017,36(2):1-16.
[5] LIU M,LEI LP,LIU D,et al.Geostatistical Analysis of CH4Columns over Monsoon Asia Using Five Years of Goast Observations[J].Remote Sensing,2016,8(5):361.
[6] BACHIR H,SEMAR A,MAZARI A.Statistical and Geostatistical Analysis Related to Geographical Parameters for Spatial and Temporal Representation of Rainfall in Semi-arid Environments:the Case of Algeria[J].Arabian Journal of Geosciences,2016,9(7):1-12.
[7] LIU RM,XU F,YU WW,et al.Analysis of Field-scale Spatial Correlations and Variations of Soil Nutrients Using Geostatistics[J].Environmental Monitoring & Assessment,2016,188(2):126.
[8] ANDERSON F.Application of Multivariate Geostatistics in Environmental Epidemiology:Case Study from Houston Texas[J].Occupational Diseases & Environmental Medicine,2016,(4):110-115.
[9] HUANG D,WANG G.Stochastic Simulation of Regionalized Ground Motions Using Wavelet Packets and Cokriginganalysis[J].Earthquake Engineering & Structural Dynamics,2015,44(5):775-794.
[10] JOURNEL A G,HUI JBREGTS C J.Mining Geostatistics[D].New York:Academic Press,1978.
[11] YIN J,NG SH,NG KM.Kriging Metamodel with Modified Nugget-effect:The Heteroscedastic Variancecase[J].Computers & Industrial Engineering,2011,61(3):760-777.
[12] 季青,余明.基于协同克里格插值法的年均温空间插值的参数选择研究[J].首都师范大学学报:自然科学版,2010,31(4):81-87.
[13] NERINI D,MONESTIEZ P,MANTé C.Cokriging for Spatial Functional Data[J].Journal of Multivariate Analysis,2010,101(2):409-418.
[14] ZHANG C,LI W,TRAVIS D.Gaps-fill of SLC-off Landsat ETM+ Satellite Image Using a Geostatistical Approach[J].International Journal of Remote Sensing,2007,28(22):5103-5122.
[15] 张小咏,刘耕年,李永化,等.高斯函数参量法及其在山区降水计算中的应用[J].地理研究,2008,27(3):594-602.
