基于量纲分析法的旋转超声磨削钛合金刀具磨损数学模型

刘凡，秦娜，牛健地，郑亮

(西南交通大学 机械工程学院，四川 成都 610031)

0 引言

钛合金因密度小、比强度高、耐高温、耐腐蚀等一系列优点，广泛应用在航空制造业中[1]。但钛合金材料亦具有导热系数小、高温化学活性大和弹性模量低等特性，是典型的难加工材料[2]。钛合金的难加工特性直接影响零部件的加工效率和加工成本。随着钛合金应用日益广泛，急需一种新的加工方法满足日益增长的钛合金市场扩展的需要。

旋转超声磨削加工是固结磨料工具的磨削加工与普通超声振动加工为一体的复合加工方式[3]。相对比传统加工钛合金的方法而言，旋转超声磨削加工具有磨削力较小、材料去除率高、加工表面质量好等突出优势，可以有效地提高刀具使用寿命与已加工表面的表面完整性，因此固结磨粒旋转超声磨削加工在许多工业领域正得到越来越广泛的应用。

1 旋转超声磨削刀具磨损

在旋转超声磨削加工中，影响刀具磨损的因素众多，例如刀具主轴转速、进给速度、超声功率、超声频率、磨料粒度、磨料类型、磨料浓度、刀具内壁厚度、刀具结合剂类型等。这些因素对超声振动刀具磨损的影响程度不尽相同，且某些因素之间存在一定的交互作用，因此将影响超声振动刀具磨损的因素全部加以考虑不现实。本文在相关预实验分析的基础上，确认了6个主要并且相对容易控制的加工工艺参数和刀具结构参数，即：刀具主轴转速(S)、进给速度(V)、超声功率(W)、超声频率(F)、磨料粒度(R)、磨料浓度(C)，将影响刀具磨损的其他因素忽略。因此旋转超声磨削刀具模型可由函数关系式(1)来表示：

T=f(S,V,P,F,R,C)

(1)

2 量纲分析法

量纲分析[9]是物理领域中建立数学模型的一种方法，在经验和试验的基础上，利用物理定律的量纲其次性原则和用于量纲分析建模的BuckinghamΠ定理，可以确定各物理量之间的关系。BuckinghamΠ定理[10]描述如下：若一个物理关系f(s1,s2,s3,…,sn)，是由一组量纲不同的物理量S1，S2，S3,…,Sn所组成。设在这组物理量中有j个量纲相互独立，并且选作为基本量纲，这个物理关系一定可以用k=n-j个无量纲量Π1,Π2,…，Πk完全表示出来，即：

f(Π1,Π2,Π3，…，Πk)=0

(2)

从 BuckinghamΠ定理来看，它是一种数学分析方法，因此量纲分析法不失为建立振动刀具磨损数学模型的有力工具。本文借助于量纲分析法确定式(1)中含6个变量的函数关系。

刀具磨损以刀具纵向长度磨损量作为刀具磨损评价指标，因此式(1)中共有7个变量，变量具体量纲见表1(应用的量纲分析系统是“质量系统”，即“LMT”系统，以L-长度量纲、M-质量量纲、T-时间量纲为3个基本物理量纲，其余物理量的量纲均为导出量纲)选取长度L、质量M、时间T为3个基本物理量纲，则由式(2)知无量纲量Π的个数是4。从7个参量中选择3个作为问题的重复变量，选取的重复变量应是线性无关的并且此线性无关物理量组成的量纲矩阵子行列式不应为0，因此根据量纲矩阵，选择S(主轴转速)、V(进给速度)、P(超声功率)作为重复变量，量纲矩阵如表2所示。

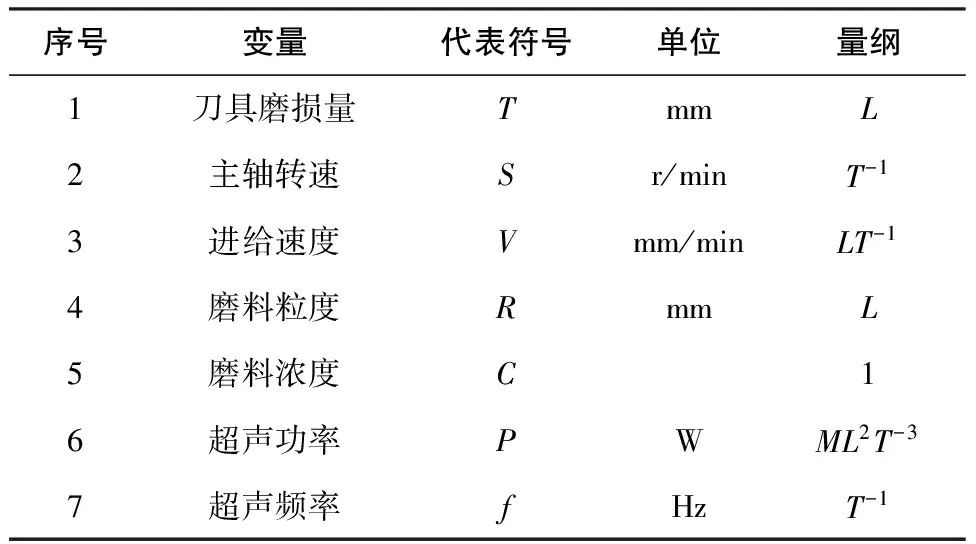
表1 变量及其量纲

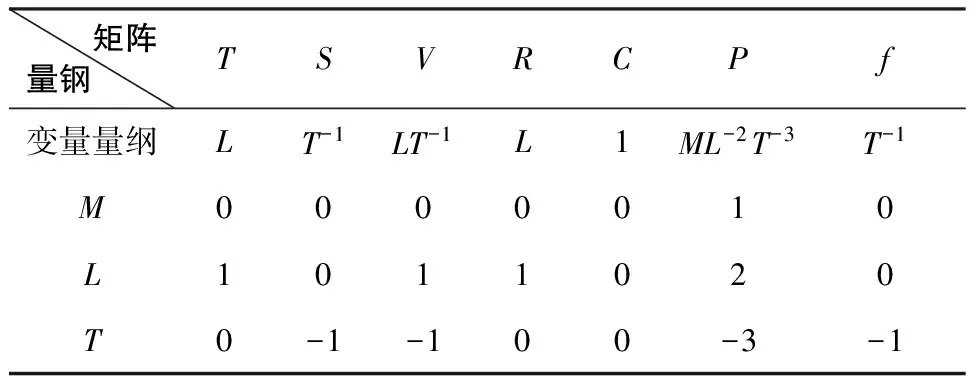
表2 量纲矩阵

根据BuckinghamΠ定理与3个重复参量写出4个无量纲量的表达式如下：

Π1=L(T-1)α(LT-1)β(ML2T-3)γ

(3)

Π2=C

(4)

Π3=T-1(T-1)α(LT-1)β(ML2T-3)γ

(5)

Π4=T-1(T-1)α(LT-1)β(ML2T-3)γ

(6)

Π为无量纲量，根据量纲一致性原理[10]可以求得Π的具体表达式，Π1的求解过程如下：

1+β=0

-α-β=0

γ=0

解之，α=1，β=-1，γ=0,则Π1=RSV-1，同理求出其余3个无量纲量Π，分别为：Π2=C，Π3=fS-1，Π4=TSV-1。则根据BuckinghamΠ定理，式(1)中刀具磨损与各参量的关系可以表示成如下关系：

f(RSV-1,C,fS-1,TSV-1)=0

(7)

式(7)转化成：TSV-1=φ(RSV-1,C,fS-1)，式中φ为某个函数，在处理试验结果或者数值结果时，通常可以把结果表示成幂次关系[11]，即：

TSV-1=C1(RSV-1)α(C)β(fS-1)γ

(8)

其中，C1是常数，而α、β、γ是实数。将式(8)转化为对数关系，即：

lnTSV-1=lnC1+αlnRSV-1+βlnC+γlnfS-1

(9)

分别令lnRSV-1=x1,lnC=x2，lnfS-1=x3，lnTSV-1=y，则式(9)可以表示为：

y=c+αx1+βx2+γx3

(10)

式(10)相对于式(1)而言，减少了自变量的个数，大大减少工作量，并且使得结果更加具有普遍性。式(10)中实数α、β、γ将通过正交试验法推导确定。

3 正交试验

正交试验设计简称正交设计(orthogonal design)，它是部分因子设计的主要方法，是利用正交表科学地安排与分析多因素试验的方法，其基本思想是从全面试验中挑选出部分有代表的点进行试验，这些点具有“均衡分散”和“整齐可比”的特点[12]。本文使用Design-expert软件设计了六因素三水平正交试验，正交试验因素水平表如表3所示。刀具磨损量为刀具旋转超声磨削钛合金前后刀具纵向长度的磨损量，超声振动刀具纵向长度的磨损量由超声振动机床中的激光对刀仪测定。根据式(10)中的替换规则，将正交试验表中试验设计与结果变换成表4所示。

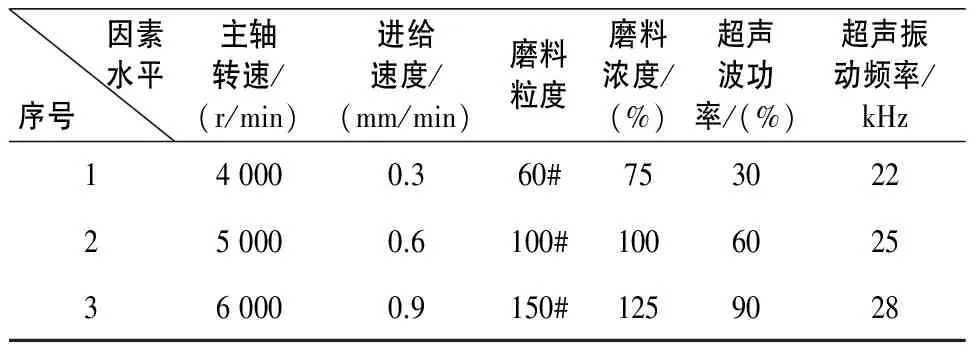
表3 因素水平编码

试验采用德国DMG Ultrasonic 70超声振动机床，超声振动刀具由郑州磨料磨具磨削研究所制备。刀具外径、内径分别为10mm和6mm，刀具结合剂类型为锡青铜基，如图1所示。工件材料为钛合金Ti6Al4V，工件尺寸为50mm×50mm×0.5mm。试验系统冷却方式为外冷，采用钛合金专用切削液。每次试验前后使用超声振动机床中的激光对刀仪测量刀具纵向长度，获得每次试验中刀具磨损量数值，每组试验重复3次，取3次实验数据的平均值作为该组试验刀具磨损结果。

表4 试验设计及结果

图1 试验用超声振动刀具

4 结果与分析

使用Design-expert软件对表4中18组刀具磨损数据进行多元线性回归建模与分析，则可拟合出旋转超声磨削钛合金刀具磨损数学模型。对式(10)进行多元线性回归分析之后模型为：

y=-6.797 14+0.634 65x1+2.549 68x2+1.855 28x3

(11)

根据上节推导，将式(11)中的系数反推到式(8)中，获得了旋转超声磨削钛合金刀具磨损数学模型，模型具体公式为：

T=e-6.797 14×S-2.220 63×V0.365 35×R0.634 65×C2.549 68×f1.855 28

(12)

模型能否实现对实际响应的预测取决于模型建立得是否合适，因此必须对模型的有效性进行检测。在Design-expert中，可以根据残差的正太概率分布是否接近一条直线来判定，如图2所示。从图中可以看出，标准残差的正态概率分布在一条直线上，充分表明了所建立的刀具磨损模型的有效性。

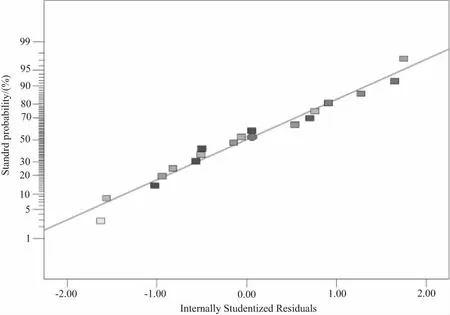
图2 标准残差概率分布图

模型的显著性反映了模型对实际响应的预测精度，因此需要对超声振动刀具磨损模型进行方差分析，判断其显著性。设显著性水平α=0.01，则模型方差分析如表5所示。

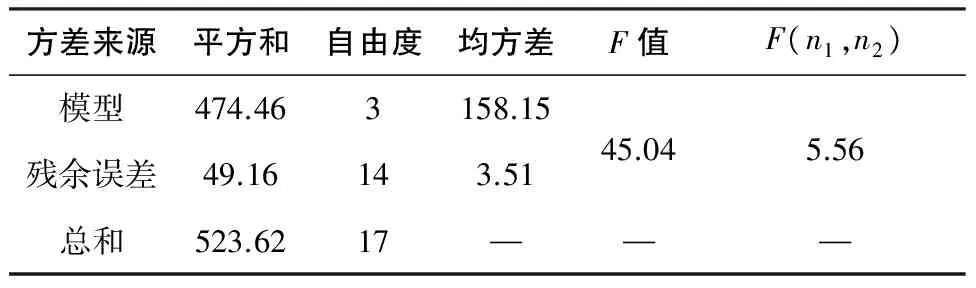
表5 模型方差分析表

根据模型和残余误差的自由度F分布表，得F0.01(3,14)=5.56,F=45.04>F0.01(3，14)=5.56，因此拟合的旋转超声磨削钛合金刀具磨损模型显著度非常明显，即可以进行振动刀具磨损量的预测。

5 结语

本文在量纲分析的基础上，以振动刀具纵向磨损量作为刀具磨损评价指标，建立了旋转超声磨削钛合金刀具磨损与刀具结构参数(磨料粒度、磨料浓度)和加工工艺参数(主轴转速、进给速度、超声功率、超声频率)的数学模型，通过有效性和显著性检验得出标准残差的正态概率分布在一条直线上，模型F分布值为45.04，在显著性水平α=0.01上，远大于F分布临界值5.56，充分表明了模型具有较高的显著度，可以对旋转超声磨削钛合金中的刀具磨损进行预测。

参考文献:

[1] 孙玉晶, 孙杰, 李剑峰. 钛合金铣削加工刀具磨损有限元预测分析[J]. 机械工程学报, 2016, 52(5): 193-201.

[2] 陈燕, 杨树宝, 傅玉灿,等. 钛合金TC4高速切削刀具磨损的有限元仿真[J]. 航空学报, 2013,34(9): 2230-2240.

[3] 秦娜. 旋转超声波磨削制孔的切削力建模与试验研究[D]. 大连：大连理工大学, 2011.

[4] 秦国华, 谢文斌, 王华敏. 基于神经网络与遗传算法的刀具磨损检测与控制[J]. 光学精密工程, 2015, 23(5):1314-1321.

[5] Zeng W M, Li Z C, Pei Z J, et al.Experimental observation of tool wear in rotary ultrasonic machining of advanced ceramics[J]. International Journal of Machine Tools & Manufacture, 2005, 45(12):1468-1473.

[6] Shen J Y, Wang J Q, Jiang B, et al. Study on wear of diamond wheel in ultrasonic vibration-assisted grinding ceramic[J]. Wear, 2015, 332/333:788-793.

[7] 荆君涛, 刘运凤, 李占杰,等. 旋转超声磨削加工中影响磨具寿命的结构参数优化[J]. 光学精密工程, 2013, 21(4):972-979.

[8] 秦娜. 钛合金固结磨粒旋转超声加中工具磨损的定量研究[J]. 学术动态, 2014(3): 32-35.

[9] 付泽民, 莫健华, 陈伟,等. 基于量纲分析法的金属板材折弯回弹数学模型[J]. 机械工程学报, 2010, 46(12):53-58.

[10] Sun B. Dimensional Analysis And Theory Of Similarity[J]. Fluid Mechanics, 2015(9):1-4.

[11] 谈庆明. 量纲分析[M]. 合肥：中国科学技术大学出版社, 2005.

[12] 何为, 唐斌, 薛卫东. 优化试验设计方法及数据分析[M]. 北京：化学工业出版社, 2012.