基于DIC的铝合金6016成形极限试验研究
2018-05-07陈天明严大伟李娟
陈天明,严大伟,李娟
(南京航空航天大学,江苏 南京 210016)
0 引言
汽车车身是汽车中用材量及质量最大的部件,约占汽车总质量的30%,所以汽车车身的轻量化对于减轻汽车自重具有重要意义[1-2]。铝合金具有质轻、耐蚀、比强度高、易加工、表面美观及回收成本低等诸多优点,汽车内外板用铝合金板代替传统使用的钢板可使整车减重10%左右,可见其减重效果十分显著[3]。系统研究铝合金的成形性能,大规模应用铝合金进行汽车覆盖件的成形具有重要意义。Mahabunphachai等人[4]研究了铝合金高温成形性能的预测,并对结果进行了有限元模拟。盈亮等[5]对6016的烘烤性能进行了详细的研究,总结出最佳烘烤强化的温度和时间。葛丽丽等[6]研究了6016铝合金的高温力学性能和成形极限。李彦波等用多元回归的方法对6016铝合金的FLD0进行了拟合,建立了FLD0的新公式。以上研究为本文提供了有益的借鉴,但以上对成形极限和力学性能的测试都是通过传统的网格坐标的方法测量的,精度和效率都不高。
数字图像相关法(digital image correlation,DIC)是一种全场动态视觉测量方法,具有非接触、精度高、受环境影响小、自动化程度高等优点,克服了坐标网格法的不足,并逐步在板料成形应变检测中得到应用。Pires等[7]采用数字图像相关法,对A5052铸造铝合金的成形性能进行了研究。Zhang[8]等在AA5086成形极限试验中应用了DIC技术,并将试验结果与基于M-K模型的有限元数值模拟结果进行了对比。DIC在金属材料的成形性能研究的应用越来的越广泛。
结合DIC设备对6016铝合金的成形极限和力学性能进行精确测量,并与不同屈服条件下理论推导得到的成形极限进行对比,找出相对准确的预测方法。
1 AA6016-T4铝合金基本力学性能
按照最新国家标准GB/T228.1-2010,分别沿板材 0°、45°及 90°轧制方向截取拉伸试样。按照 GB/T5027—2007 和GB/T5028—2008 标准测定应变强化系数n、塑性应变比r,以上试验均遵照 GB/T228—2002 金属拉伸室温试验法进行单向拉伸试验测定。AA6016-T4铝合金的基本力学性能如表1所示。
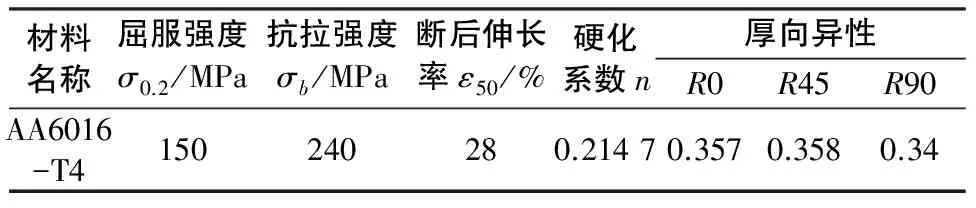
表1 AA6016的力学性能
2 FLD的理论计算
2.1 Swift和Hill失稳极限
板材在冲压成形的塑性变形过程中,由于塑性变形不能稳定地进行,往往会导致板材的起皱或者拉裂。拉伸失稳是板材成形失效的最主要方式,因此关于这方面的理论有很多,其中最有代表性的是Swift的分散性颈缩失稳理论和 Hill 的集中性颈缩失稳理论。
将在Hill48屈服准则下的等效应力式带入Swift分散性失稳准则,得到在Hill48下的Swift失稳极限。
式中:ε1——主应变;
ε2——次应变;
r0——0°方向的各向异性指数;
r90——90°方向的各向异性指数;
n—— 硬化指数。
带入Hill集中性失稳准则得到在Hill48下的Hill失稳极限。
2.2 基于Hill79屈服准则的极限计算
将Hill79屈服准则下的等效应力带入到Hill集中性失稳准则,得到在Hill79下的失稳极限:
将Hill79屈服准则下的等效应力带入到Swift分散性失稳准则,得到在Hill79下的失稳极限:
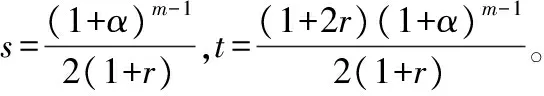
当σ1>σ2>0,m为大于1的材料参数可以通过以下求得:
式中:σ0为抗拉强度,MPa;σs为屈服强度,MPa。
2.3 基于keeler公式的成形极限计算
根据keeler公式:
t≤ 2.5时,FLD0=(23.3+14.13t)×n/0.2
2.5≤t≤5.5时,FLD0=(20+20.67t-1.94t2)×n/0.2
t>5.5时,FLD0=75.13×n/0.21
式中t为试样厚度,mm。
3 FLD的实验获得
实验室用的材料AA6016由西南铝业提供,通过单向拉伸实验得到其基本力学性能见表1。材料的厚度为1 mm。试件参考ISO 12004-2: 2008( GB /T 24171. 2-2009) 标准经线切割制备而成。试件表面喷涂黑、哑光白漆形成黑白相间的散板图案,作为数字图像相关法匹配和跟踪被测件表面变形的特征。
板料成形采用Nakazima实验法,即半球刚性凸模胀形实验。通过改变试件的宽度使其侧向约束改变,从而得到从单拉到等双拉的成形极限。润滑采用先在试件和冲头之间涂上润滑脂的方法,再给冲头和试件之间贴上硅胶垫。将试件安装到成形极限上,对中并夹紧后,启动实验机的同时开启相机,采集不同宽度试件在成形过程不同时刻的图像(不同变形状态)。成形极限机的冲头速度设为1mm/s,压边力设置为250kN,相机采集频率为15帧。
通过aramis软件的flc功能生成材料在不同宽度下的成形极限处的主应变,如图1所示;通过flc功能生成对应的flc曲线如图2所示。

图1 不同宽度的AA6016试样在ARAMIS 软件上的极限应变云图
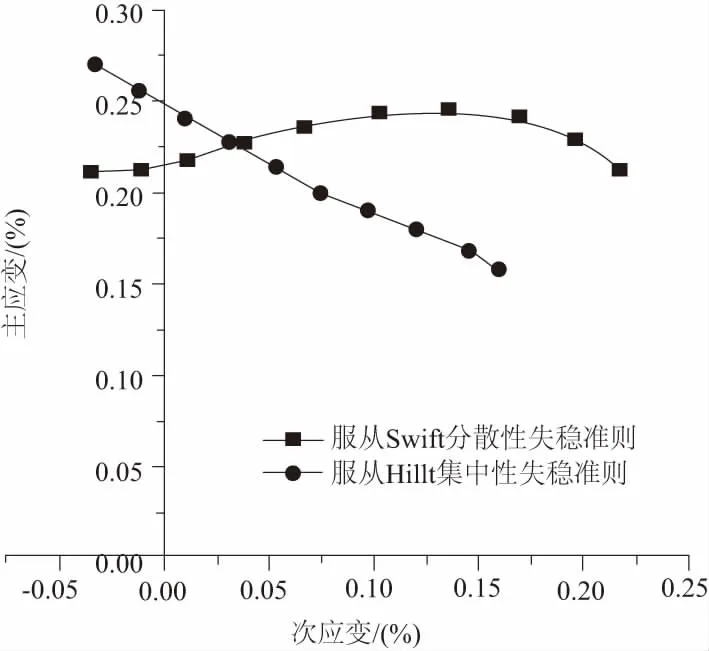
图2 服从Hill48屈服准则
4 理论计算和实验的对比
将基本力学性能带入到Hill和Swift失稳极限公式中,就可以求得材料的各种屈服准则和失稳准则下的极限应变值。计算出各种条件下的极限应变值后,将这些极限应变点(ε1,ε2)绘制在ε1-ε2坐标系中,并且拟合成一条光滑的曲线就得到6016铝合金在常温下的成形极限图(FLD)。其中图3是材料服从Hill48屈服准则,且分别服从Swift分散性失稳准则和Hill集中性失稳准则的相应FLD;图4是材料服从Hill79屈服准则,且分别服从Swift分散性失稳准则和Hill集中性失稳准则的相应FLD。
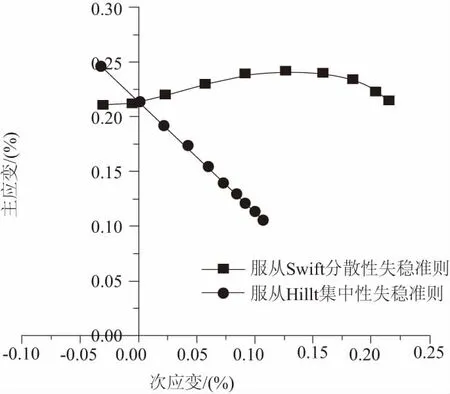
图3 服从Hill79屈服准则
在单向拉伸应力状态和靠近单向拉伸的平面拉伸应力状态时,运用Hill集中性失稳理论来求解极限问题;在等双拉伸应力状态和靠近等双拉伸的平面拉伸应力状态时,运用Swift分散性失稳理论来求解极限问题。因此将两者合并而成形得到完整的FLD,如图4所示。满足keeler公式的FLD如图5所示。由DIC设备测量得到的实验的FLD曲线如图6所示。将上述曲线在一张图中描述,如图7所示。
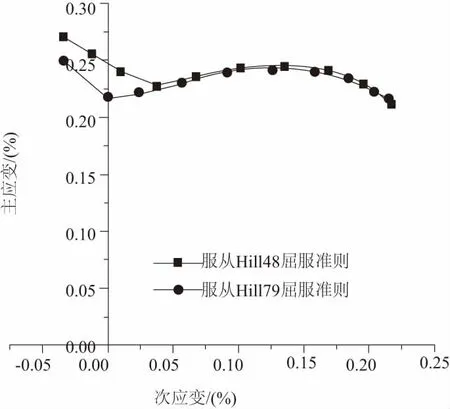
图4 服从两种屈服准则的完整FLD
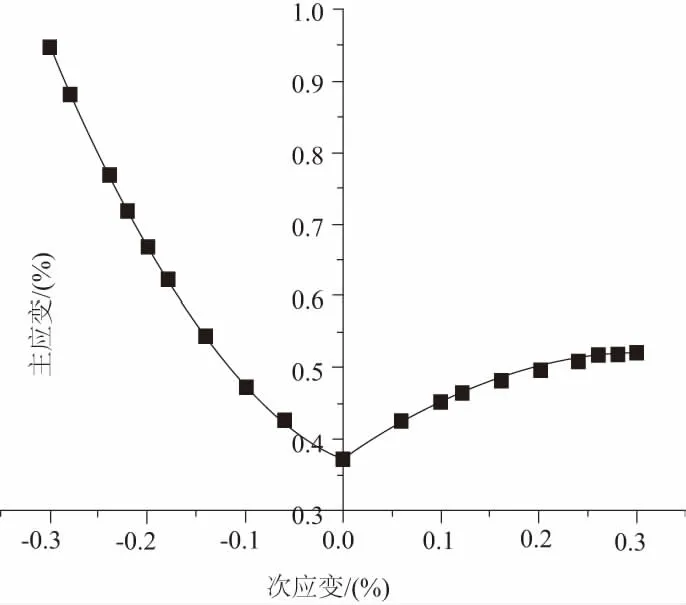
图5 满足Keeler经验公式的FLD
5 结语
1) DIC设备测量得到的6016铝合金的FLC曲线位于由Keeler公式预测的FLC曲线的下方,并且有较大的误差,左侧的误差率在16%左右,右侧的误差比较大,但总体趋势大体一致。
2) DIC设备测量得到的6016铝合金的FLC曲线位于由Hill48和Hill79预测的FLC曲线的上方,并且有较大的误差,左侧的误差率分别是34%和36%,右侧的误差在18%左右,总体趋势大体一致。
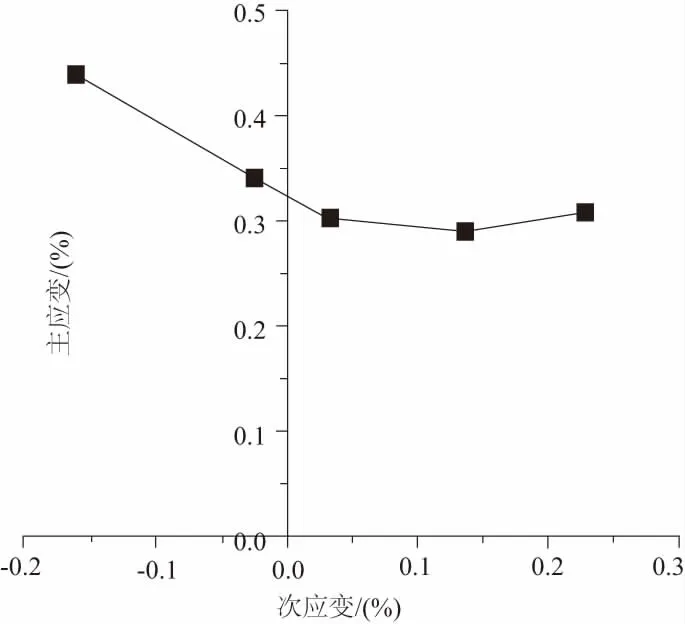
图6 实验测得的FLD
3) 在使用理论预测6016铝合金的FLC时候,无论是Keeler还是Hill48或Hill79都无法做到准确预测,但是采用Hill48或Hill79预测的结果比较安全。
4) keeler公式得到的曲线相对更加接近实验数据,但是其右侧部分和实验数据趋势相差较大,表明keeler公式并不适用于铝合金的预测。
参考文献:
[1] 时张杰,童国权. 铝合金AA5083超塑性变形力学特性[J]. 机械制造与自动化,2007,36(6):25-28.
[2] 丁向群,何国术,陈成封,等. 6000系汽车车用铝合金的研究应用进展 [J]. 材料科学与工程学报,2005,23(2):302-305.
[3] 韦韡,蒋鹏,曹飞. 6082铝合金的高温本构关系[J]. 塑性工程学报,2013,20(2):100-106.
[4] Mahabunphachai S, Koç M. Investigations on forming of aluminum 5052 and 6061 sheet alloys at warm temperatures [J]. Materials and Design, 2009, 31(5): 2425-39.
[5] 盈亮, 申国哲, 胡平, 等. AA6016铝材烘烤硬化性能研究 [J]. 机械工程学报, 2011, 1(10): 19-24.
[6] 赵培峰,任广升,沈智,等. 6061铝合金热压缩变形条件对流变应力的影响及其本构方程的研究[J]. 塑性工程学报. 2007,14(6):130-133.
[7] Pires G, Robert M, Arrieux R. Studies on drawing of the aluminum A 5052 alloy in the thixocast condition [J]. Journal of Materials Processing Technology, 2004, 157(51): 596-603.
[8] Zhang C, Leotoing L, Zhao G, et al. A methodology for evaluating sheet formability combining the tensile test with the M-K model [J]. Materials Science & Engineering A, 2010, 528(1): 480-485.
