考虑初始迎角影响的二维翼型跨声速颤振边界预测

高国柱, 白俊强, 李国俊, 刘南, 李宇飞

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.中航工业空气动力研究院, 辽宁 沈阳 110034)

在现代飞行器设计中，随着巡航速度的逐步提高及结构重量系数的降低，机翼颤振问题日益突出，极易造成结构破坏而引发灾难性的后果，严重影响了飞行安全。所以，在飞行器设计过程中，严格要求在飞行包线内不能出现颤振现象，且必须留有一定的颤振裕度，颤振边界成为约束飞行包线的一个重要因素。然而，目前大量的民用和军用运输机都在跨声速区域巡航飞行，跨声速飞行时的非定常激波运动及附面层分离会导致颤振裕度远远低于其他速度区域，且经常引发各种复杂的非线性颤振现象[1-3]，显著地影响飞行安全和任务性能，对跨声速颤振边界的预测以及颤振特性分析成为近年的研究热点。

传统的飞行器的颤振分析一般在零度迎角下计算和试验[4]，忽略了来流非零迎角对颤振边界的影响。然而飞行器翼型和风力机叶片经常在非零迎角状态下工作，平衡位置与零迎角不同，颤振边界也会随之改变。如果在飞行器的颤振设计校核阶段不对迎角影响加以考虑，可能导致设计出来的飞行器存在颤振安全隐患，导致结构破坏，严重时会造成机毁人亡。

20世纪90年代，基于Euler/RANS方程的颤振数值模拟方法逐渐成熟，研究人员针对不同的构型进行了大量的数值模拟，但是针对流动过程中自由来流非零迎角影响的颤振问题则鲜有深入研究。首先有针对性、目的性和全面性地对此类问题展开研究的学者是NASA的Langley研究中心的Edwards等人[5]。早在1983年，Edwards基于跨声速小扰动方程，采用时域方法研究了马赫数和迎角对颤振边界的影响。Edwards等人的计算结果表明在马赫数0.775到0.800之间，增加1.5°迎角会导致颤振临界速度降低50%。1999年，Dowell等人[6]研究了间隙非线性引起的极限环振荡时，迎角逐渐增加会引起颤振临界速度的改变以及由此引起的一系列非线性行为。2002年，Dowell等人[7]进一步研究了低速时迎角改变对颤振边界的影响。2006年，Park等人[8]研究有间隙的三维全动控制舵面在亚声速和跨声速区内，初始迎角变化对气动弹性响应特性的影响。2013年，Bichiou等人[9]采用非定常涡格法，研究了迎角对颤振临界速度和极限环幅值的影响，结果表明，迎角增加会使得颤振临界速度提高、极限环幅值减小。

国内从20世纪90年代开始研究迎角对颤振临界速度的影响。在1996年，杨永年采用非线性涡格法探究了大迎角颤振分析方法。在2004年，叶正寅[10]通过风洞试验和数值模拟研究了在低速情况下，随着迎角的增加，颤振临界速度先略有上升，在静态失速点附近，颤振临界速度大幅度下降，迎角进一步增加后，颤振临界速度又上升。在2007年，叶正寅和张陈安的研究结果表明在较高雷诺数的全湍流条件下，NACA0012翼型在气动力的线性段，颤振临界速度随迎角增加略有上升，但在接近失速迎角附近时，颤振临界速度则随迎角增加快速下降。在2008年，张伟伟等人[11]采用系统辨识方法计算削尖三角翼的颤振临界速度，研究表明迎角增加使得颤振临界速度减小。在2011年，张伟伟等人[12]基于当地活塞理论研究了典型超声速舵面的颤振特性，结果表明在舵面无间隙时，平均迎角为20°时的颤振速度比5°的颤振速度低8.3%；在舵面有间隙时，迎角越大，激发极限环运动所需的初始扰动越大。2012年，刘畅畅等人[13]通过低速风洞试验研究了迎角改变对普通翼型NACA0012和风力机翼型NREL S809的颤振特性的影响。

虽然针对考虑迎角影响的颤振研究已经取得了一定的成果，但是大部分研究工作仍然停留在考虑迎角影响的低速和超声速颤振边界预测，对于在跨声速区域内颤振边界预测和影响机制缺乏深入的认识。本文基于非定常RANS方程和结构运动方程，建立时域气动弹性分析方法。使用该方法对Isogai案例A模型[14-15]的零迎角和考虑非零迎角影响的跨声速颤振边界进行研究，并从激波和分离流动的角度分析迎角对颤振特性的影响机制。

1 流场求解

1.1 非定常气动力求解

本文采用课题组自研的CFD代码-TeAM求解非定常气动力，其控制方程是三维可压缩非定常积分形式的N-S方程：

∬Ω∂Q∂t+∂(F-Fv)∂x+∂(G-Gv)∂y+∂(H-Hv)∂zdΩ=0

(1)

式中,Q=ρρuρvρweT为守恒向量,ρ,(u,v,w)和e分别为密度、直角坐标系下的速度分量和单位质量气体的总能量。F,G,H是3个方向的无黏矢通量,Fv,Gv,Hv是3个方向的黏性矢通量。其中无黏项采用Roe格式进行离散,黏性项采用二阶中心差分进行离散,时间推进采用双时间步法进行迭代求解,为封闭方程引入k-ωSST湍流模型。为了进一步提高计算效率,采用多重网格加速收敛技术、并行计算技术。

1.2 跨声速非定常气动力的精度验证

准确预测非定常气动力是气动弹性分析的基础,首先以NACA64A010强迫俯仰运动[16]为例,研究网格对气动力的影响。参照阻力预测会议发布的网格生成标准得到的3套网格:粗网格、中等网格和密网格,其中中等网格如图1所示。算例以Davis发布的中等非线性算例(存在激波)的CT6为准。翼型强迫振动的迎角随时间的变化方程为α(t)=α0+αmsin(ωt),k=ωb/V∞,其中α0为翼型初始迎角,αm为翼型强迫振动振幅,ω为翼型强迫振动角频率,参考长度b为翼型的半弦长,k为减缩频率,xa/c为转轴位置。计算状态为:Ma∞=0.796,α0=-0.21°,αm=1.01°,k=0.202,xa/c=0.248。

参考文献仅提供了CT6的非定常气动力随俯仰角的试验结果。计算结果与试验结果对比如图2和图3所示,升力系数随迎角变化曲线的计算结果与试验吻合较好。但是力矩曲线有一定的差别,从和试验结果的对比可见,本文的计算结果与Bendiksen[1]吻合较好,关于和试验结果的差别问题,Bendiksen[1]认为通过目前的湍流模型和薄层N-S方程无法预测图中非定常力矩的“膨胀部分”,当然还有可能是风洞试验的不足。由CT6结果可见,中等网格对激波运动的模拟精度与密网格基本一致,而粗网格则有所欠缺。同时,该算例的计算结果验证了本文发展的求解方法对跨声速非定常气动力的计算具有较高的精度。

图1 NACA64A010翼型中等网格示意图 图2 NACA64A010翼型升力系数随迎角变化曲线 图3 NACA64A010翼型俯仰力矩系数随迎角变化曲线

2 结构运动方程

以具有浮沉h和俯仰α2个自由度的典型的二元翼段来作为颤振的研究对象,该二元机翼颤振系统如图4所示。具有浮沉和俯仰两自由度的二维翼型结构运动方程为:

m+Sα+Dh+Khh=-L

(2)

Sα+Iα+Dα+Kαα=My

(3)

式中，m为机翼质量,Sα为二维翼型对刚心的质量静矩,Dh为浮沉阻尼,Kh为翼型关于刚心的沉浮刚度,Iα为二维翼型对刚心的质量惯性矩,Dα俯仰阻尼,Kα为翼型关于刚心的俯仰刚度,L为升力,My为俯仰力矩。

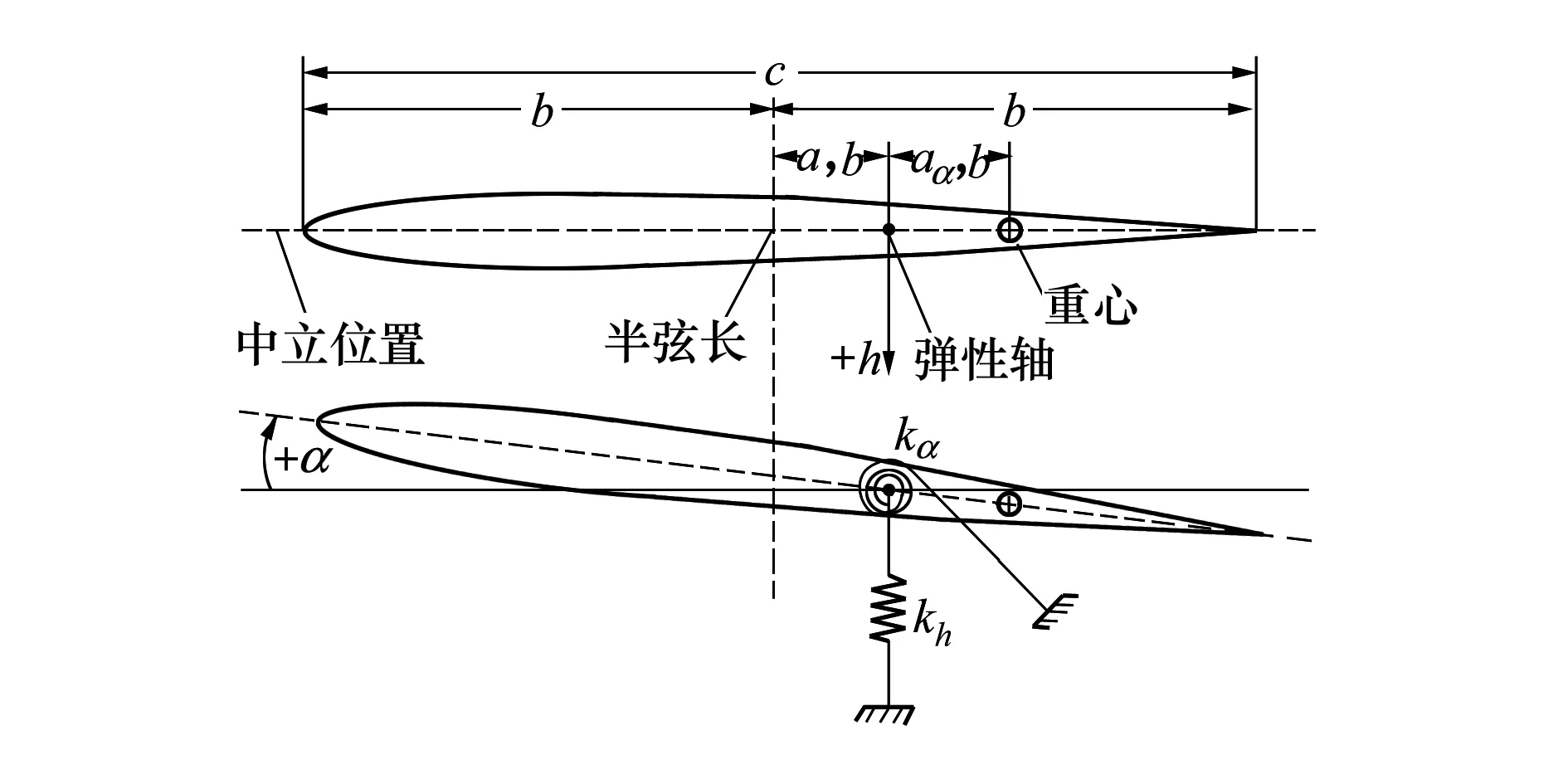
图4 二维翼型沉浮/俯仰两自由度颤振问题几何和结构参数定义[17]

针对上述二维两自由度翼型结构运动方程,进行无量纲化可得:

M+D+Kq=Q

(4)

式中

q=hb

αM=1xα

D=2ζhωh0

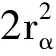
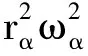
Q=-Lmb

Mymb2

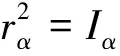
无量纲颤振速度定义为:

Vf=U∞μωαb

(5)

式中，U∞为自由来流速度,μ=m/πρ∞b2为质量比,ρ∞为自由来流密度。

为了便于时域求解,引入状态变量x=q

=f(x,t)=A·x+B·F

(6)

式中，A=0I

-M-1K-M-1D,B=0

M-1,F=0

Q。

本文采用基于预估-校正技术的四阶隐式Adams线性多步法[18]对方程(6)进行时域推进求解:

n+1=xn+Δt24(55fn-59fn-1+37fn-2-9fn-3)=xn+Δt24(55A·xn-59A·xn-1+

37A·xn-2-9A·xn-3)+Δt24(55B·Fn-59B·Fn-1+37B·Fn-2-9B·Fn-3)

xn+1=xn+Δt24[9f(n+1,t+Δt)+19fn-5fn-1+fn-2]=xn+Δt24(9A·n+1+19A·xn-

5A·xn-1+A·xn-2)+Δt24(55B·Fn-59B·Fn-1+37B·Fn-2-9B·Fn-3)

(7)

该方法既保证了方程的求解效率,又具有较好的鲁棒性。

在有迎角的情况下,翼型除动态位移外,定常气动力会产生静变形位移。在计算过程中,必须考虑静变形带来的影响。计算静变形时,只需将方程(4)的动态项去掉,即可得到静变形位移量:

Kqs=Q

(8)

对于不同迎角的气动弹性数值模拟,先采定常流场程序,计算定常状态下的流场,等待流场基本稳定后,启动计算翼型静变形程序。当翼型静变形计算收敛后,给翼型一个扰动,翼型就会在气动力、惯性力和弹性力三者的共同作用下进入动态响应过程。根据响应的特征,判断是否发生颤振,从而得到颤振临界速度。

3 跨声速颤振边界验证

跨声速颤振凹坑[19-20]与空气的可压缩性和激波相位滞后效应密切相关,因此跨声速颤振边界预测的关键在于激波捕捉的准确性。本文首先对Isogai案例A模型的跨声速颤振边界进行预测,以验证本文颤振计算方法的可靠性。其中计算采用k-ωSST湍流模型,结构参数采用文献[21]中的参数,雷诺数按照文献[22]中对所有马赫数给定为6×106。计算网格为上述非定常气动力验证时所用的中等网格,如图1所示。

图5和图6分别为在零迎角条件下计算得到的颤振速度边界和颤振频率比边界,与参考文献[22-23]的结果吻合较好。颤振边界表现为“双台阶”形,在Ma=0.84和0.91处颤振速度出现2次跃升,与Timme等的计算结果吻合较好。可以把颤振边界大致分为4个区域[24]:①亚声速区域Ma<0.80;②跨声速凹坑Ma=0.80～0.83;③第一次颤振速度跃升区域Ma=0.84～0.91;④锁定区域Ma>0.91。

第一次颤振速度跃升(Ma>0.83)与翼型表面分离流动的出现和扩大密切相关。图7展示了5个不同马赫数下的表面摩阻分布对比,图8展示了颤振边界和准定常升力线斜率随马赫数变化曲线。从图中结果可以看出,当0.83≤Ma≤0.87时,随着马赫数增大,翼型表面的分离区扩大,使得升力线斜率急剧减小,导致颤振边界急剧增大。

图5 颤振速度边界(α0=0°) 图6 颤振频率比边界(α0=0°)图7 不同马赫数下的表面摩阻分布对比(α0=0°)

能量概念在理解和解释颤振问题中具有重要地位,Bendiksen[25]针对跨声速颤振提出了“跨声速稳定性法则”(transonic stabilization laws),从气动力做功的角度分析振动机理,研究了气动力的幅值及相位和颤振稳定性之间的关系,此处的相位指的是机翼俯仰力矩相对于俯仰位移的滞后相位角。本文采用类似的分析方法对Isogai案例A模型在零迎角和非零迎角条件下的跨声速稳定性进行分析,其中k为减缩频率。

为了分析颤振速度随迎角变化的原因,以Isogai翼型的简谐强迫俯仰运动为研究对象,分析不同马赫数下气动力对翼型的做功情况。通过力矩系数的幅值和相位差能反映俯仰力矩对翼型的做功情况。由于俯仰轴位于翼型前缘前,必然在气动中心之前,也就是说翼型抬头产生的是低头力矩,反之亦然,所以Isogai翼型的俯仰运动和纵向俯仰力矩在定常情况k=0时就具有180°的相位差。图9、图10和图11分别为俯仰运动中力矩系数的幅值、相位以及做功情况随马赫数变化曲线。

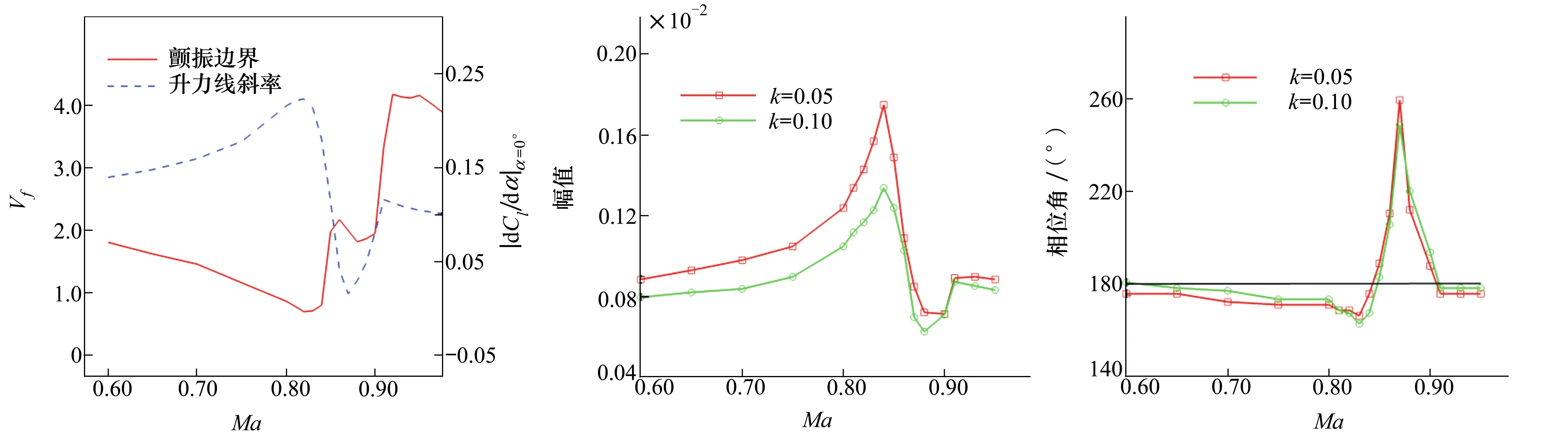
图8 颤振边界和准定常升力线斜率随马赫数变化曲线 图9 俯仰运动中力矩系数的幅值随马赫数变化曲线(α0=0°) 图10 俯仰运动中力矩系数的相位随马赫数变化曲线(α0=0°)

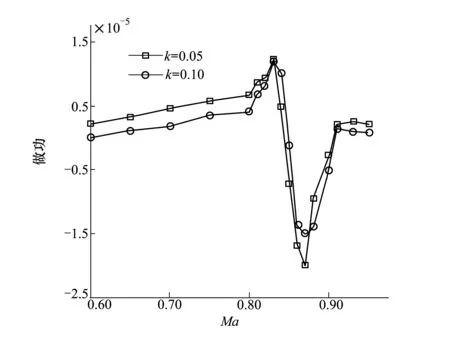
图11 俯仰运动中气动力做功随马赫数变化曲线(α0=0°)

当来流马赫数Ma<0.80时,流场无激波,但随马赫数的增加,流动压缩性的影响使力矩幅值缓慢增大,相位差的变化不明显(10°以内),气动力对翼型做功也逐渐增加,因此颤振速度随马赫数的变化趋势由压缩性主导。

当Ma=0.80～0.84时,激波的往复运动导致力矩幅值明显增大,且出现了显著的相位滞后,气动力对结构输送的能量显著增加,颤振边界出现“跨声速凹坑”。

当Ma=0.85～0.91时,激波诱导的附面层分离占据主导地位,激波后方分离区域不仅大幅降低了力矩幅值,还带来了极大的相位滞后,导致气动力对翼型的做功降低,使颤振速度大幅提高。

当Ma≥0.91时,空间马赫数云图如图12所示。

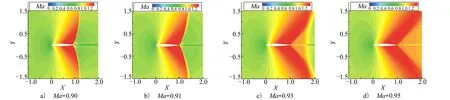
图12 迎角为0°时马赫数云图

由图可以看出,此时激波达到翼型后缘,流场进入“冻结区域”(freeze region),以致翼型运动对激波和压力分布的影响很小,翼型上下表面非定常压力分布的幅值和相位差都维持在较小的量级,力矩系数的幅值、相位差以及做功也非常小。从图10中可以得知,在“冻结区域”的相位角均接近180°,这意味着此时气动力基本不做功,系统处于临界稳定状态,翼型的颤振速度随马赫数变化很小。

4 考虑迎角影响的跨声速颤振边界预测

初始迎角对跨声速激波位置、强度以及翼型表面分离流动有很大的影响,进而会影响跨声速颤振边界。本文对Isogai案例A模型进行考虑迎角影响的跨声速颤振边界的数值模拟。为了消除网格带来的影响,采用与零迎角计算所用相同的气动网格进行数值模拟。结构参数以及气动参数和零迎角计算保持一致。

图13和图14分别为零迎角和非零迎角条件下计算得到的颤振速度边界对比图和频率比对比图。数值模拟结果表明,考虑迎角影响计算得到的颤振边界较零迎角计算得到的颤振边界在Ma≤0.73时基本保持不变;当0.73≤Ma≤0.76时,随着初始迎角增加,颤振速度减小,最大可减小12.5%;当0.77≤Ma≤0.86时,随着初始迎角增加,颤振速度较零迎角时逐渐增加,在零迎角时跨声速凹坑最低点的位置(Ma=0.83)颤振速度增幅最大,增加了124%,即初始迎角影响使得跨声速凹坑程度削弱,且跨声速凹坑最低点前移;当0.87≤Ma≤0.90时,考虑初始迎角影响的颤振边界较零迎角颤振边界上移,第2个凹坑程度削弱;当Ma≥0.91时,考虑初始迎角影响的颤振边界较零迎角的偏大。

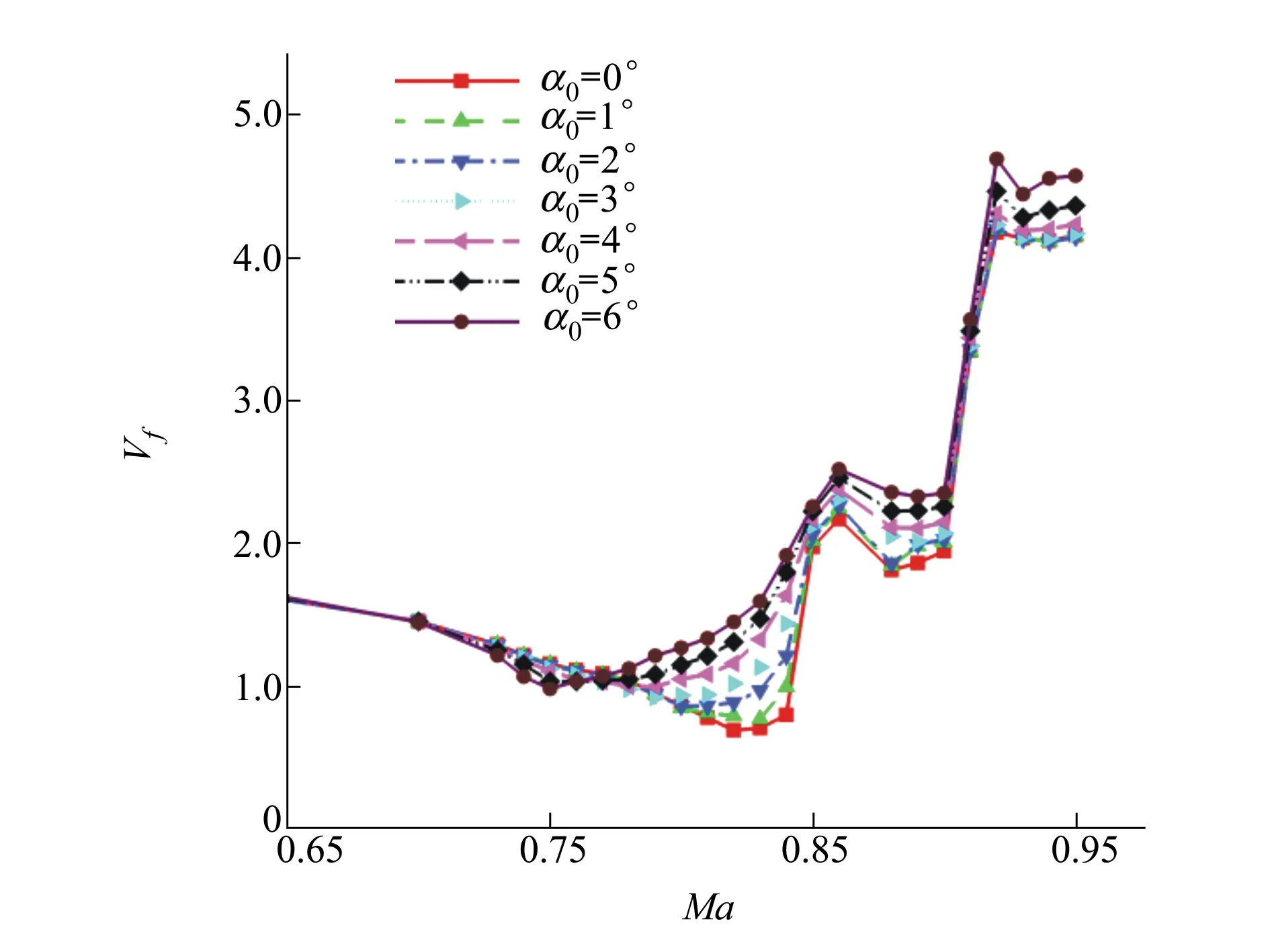
图13 颤振速度边界

图14 颤振频率比边界

为了探究初始迎角影响引起跨声速颤振边界变化的原因,选取4个典型的马赫数进行不同迎角发生颤振时的静变形计算结果对比,分别为Ma=0.70,0.78,0.83,0.94。

当Ma=0.70时,如图15a)所示,颤振临界速度随初始迎角增加时先基本保持不变,当初始迎角增加到4°时,颤振临界速度开始减小。从图16a)和图17a)可以看出,当初始迎角小于4°时,静变形后激波强度变化不明显,而且翼型表面无分离流动,此时由于激波和分离的共同作用,使得颤振临界速度变化不明显。当初始迎角大于4°时,静变形后激波强度迅速增加,翼型上表面出现小范围的分离流动,此时激波强度变化占据主导地位,随着迎角增加,颤振临界速度逐渐减小。

当Ma=0.78时,如图15b)所示,颤振临界速度随初始迎角增加而先减小后增加。从图16b)和图17b)可以看出,当初始迎角小于3°时,静变形后翼型表面无分离,但是激波强度随着迎角的变化而迅速增强,导致颤振临界速度随着迎角增加而逐渐减小。当初始迎角大于4°时,静变形后激波强度随着迎角变化不明显,但是分离区迅速扩大。此时分离流动的影响占据主导地位,使得颤振临界速度增加。

当Ma=0.83时,如图15c)所示,处于零迎角时跨声速凹坑内,颤振临界速度随着初始迎角增加而剧烈增加。从图16c)和图17c)可以看出,随着初始迎角增加,静变形后激波强度变化不大,但在翼型上表面出现分离流动,并且分离区迅速扩大。此时分离流动的影响占据主导地位,颤振临界速度则随着初始迎角逐渐增加。

当Ma=0.94时,如图15d)所示,颤振临界速度随着初始迎角增加而小幅增加。从图16d)和图17d)可以出,此时静变形后激波强度变化不大,但在翼型上表面的后缘处出现分离流动。此时由于分离区的影响,颤振临界速度则随着迎角增加逐渐略有上升。

图15 颤振速度边界和颤振频率比边界随迎角变化曲线

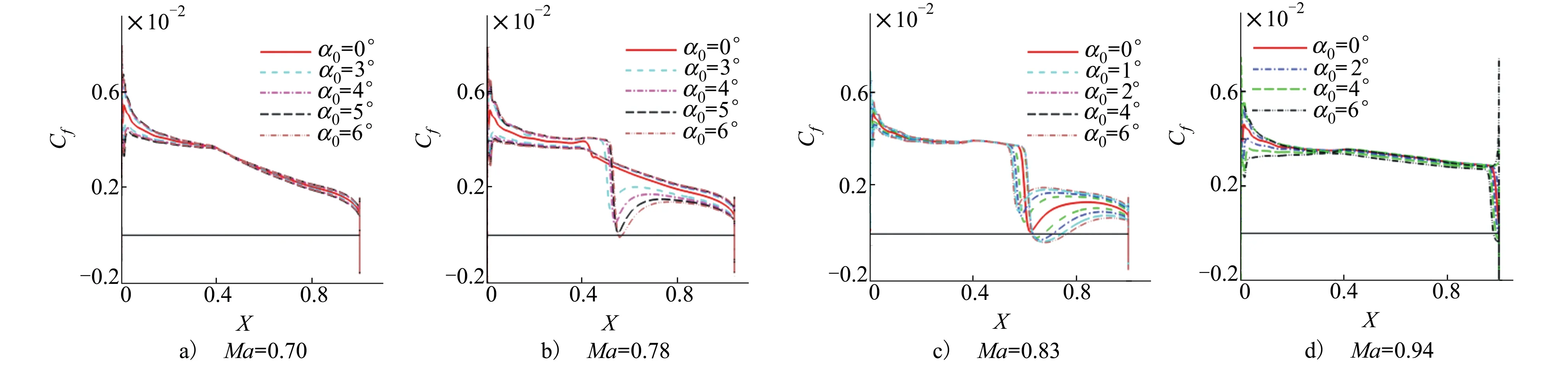
图16 静变形后表面摩阻分布随初始迎角变化曲线

图17 静变形后压力系数随初始迎角变化曲线

5 结 论

本文基于RANS方程和结构运动方程,建立时域气动弹性分析方法,分别对零迎角和考虑非零迎角影响的Isogai案例A模型的跨声速颤振边界进行预测,数值模拟结果表明:

1)本文采用零迎角计算得到的颤振边界和文献的结果吻合很好,验证了本文建立方法的可靠性。

2)在Ma≤0.73时迎角变化对颤振临界速度基本没有影响;当0.73≤Ma≤0.76时,随着初始迎角增加,颤振临界速度减小;当0.80≤Ma≤0.86时,考虑初始迎角影响,颤振速度较零迎角时增加,非零迎角影响使得跨声速凹坑程度削弱,且跨声速凹坑最低点前移;当0.87≤Ma≤0.90时,考虑初始迎角影响的颤振边界较零迎角颤振边界上移,第2个凹坑程度削弱;当Ma≥0.91时,非零迎角影响的颤振速度较零迎角的增加。

3)无论迎角是否为零,当激波到达翼型后缘,进入冻结区域,气动力对翼型几乎不做功,系统处于临界稳定状态,相同迎角下的颤振速度随马赫数的增大而变化很小。

4)结果表明,在更高的马赫数下,增加初始迎角,会增加系统的稳定性。这也表明增加初始迎角可以提高颤振临界速度,从而作为一种抑制颤振的手段。

综上所述,激波和翼型表面的分离现象共同作用,影响了翼型的颤振特性,其中激波增强会降低系统的稳定性,分离区域的扩大会增加系统的稳定性。来流迎角对激波强度和翼型表面分离区域大小均有影响,使得翼型的气动力非线性增强,颤振特性与零迎角条件下有明显区别。

因此针对机翼进行颤振设计时,需要对来流迎角的影响加以考虑,以便得到精确的颤振边界,确保飞机的飞行安全。

参考文献：

[1] Bendiksen O O. Review of Unsteady Transonic Aerodynamics: Theory and Applications[J]. Progress in Aerospace Sciences, 2011, 47: 135-167

[2] Bendiksen O O. Transonic Flutter Characteristics of Advanced Fighter Wings[C]∥56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Florida, 2015

[3] Cunningham A M. The Role of Non-Linear Aerodynamics in Fluid-Structure Interaction[C]∥29th AIAA Fluid Dynamics Conference, 1998

[4] 叶正寅, 赵令诚. 亚音速、时间域内机翼的气动弹性分析方法[J]. 西北工业大学学报, 1989, 7(4):456-463

Ye Zhengyin, Zhao Lingcheng. Aeroelastic Characteristics of Wings in Subsonic Flow[J]. Journal of Northwestern Polytechnical University, 1989, 7(4): 456-463 ( in Chinese)

[5] Edwards J W, Bennet R M, Whitlow W, et al. Time-Marching Transonic Flutter Solutions Including Angle-of-Attack Effects[J]. Journal of Aircraft, 1983,20(11): 899-906

[6] Kholodar D B, Dowell E H. Behavior of Airfoil with Control Surface Freeplay for Nonzero Angles of Attack[J]. AIAA Journal, 1999, 37(5): 651-653

[7] Dowell E, Tang D. Nonlinear Aeroelasticity and Unsteady Aerodynamics[C]∥40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, 2002

[8] Park Y, Yoo J, Lee I. Effects of Angle-of-Attack on the Aeroelastic Characteristics of a Wing with Freeplay[J]. Journal of Spacecraft and Rockets, 2006, 43(6): 1419-1422

[9] Bichiou Y, Nuhait A, Abdelkefi A, et al. Unsteady Aeroelastic Behaviors of Rigid Airfoils with Preset Angles of Attack[J]. Journal of Vibration and Control, 2016, 22(4): 1010-1022

[10] 叶正寅. 不同迎角下翼型的气动弹性性质研究[C]∥首届全国航空航天领域中的力学问题学术研讨会, 成都, 2004: 240-242

Ye Zhengyin. The Study of Aeroelastic Property of Airfoil at the Different Angles of Attack[C]∥The 1st Proseminar about the Mechanical Problems in the Fields of Aeronautics and Aerospace, Chengdu, 2004: 240-242 (in Chinese)

[11] Zhang W, Ye Z. Effects of Angles of Attack on Flutter Characteristics of a Cropped Delta Wing[C]∥49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, 2008

[12] 张伟伟, 王忠波, 叶正寅, 等. 迎角对间隙舵面的非线性颤振特性影响研究[J]. 机械强度, 2011, 33(2):296-301

Zhang Weiwei, Wang Zhongbo, Ye Zhengyin, et al. Effect of Angle of Attack on Flutter Characteristics of a Control Surface with Free-Play Nonlinearity[J]. Journal of Mechanical Strength, 2011, 33(2):296-301 (in Chinese)

[13] 刘畅畅, 刘子强, 季辰. 不同迎角的翼型气弹特性风洞试验研究[J]. 空气动力学学报, 2012,30(2):271-276

Liu Changchang, Liu Ziqiang, Ji Chen. Aeroelastic Characteristics of Airfoils at Different Angles of Attack in Wind Tunnel Testing[J]. Acta Aerodynamica Sinica, 2012,30(2): 271-276 (in Chinese)

[14] Alonso J, Jameson A. Fully-Implicit Time-Marching Aeroelastic Solutions[R]. AIAA-1994-0056

[15] Zhang Zhichao, Yang Shuichi, Liu Feng. Prediction of Flutter anf LCO by an Euler Method on Non-Moving Cartesian Grids with Boundary-Layer Corrections[R]. AIAA-2005-0833

[16] Davis S S. NACA 64A010(NASA AMES model) Oscillatory Pitching[R]. AGARD Report No. 702

[17] Thomas J P, Dowell E H, Hall K C. Nonlinear Inviscid Aerodynamic Effects on Transonic Divergence, Flutter, and Limit-Cycle Oscillations[J]. AIAA Journal, 2002, 40(4): 638-646

[18] 叶正寅, 张伟伟, 史爱明,等. 流固耦合力学基础及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2010:171-173

Ye Zhengyin, Zhang Weiwei, Shi Ai′ming, et al. Fundamentals of Fluid-Structure Coupling and Its Application[M]. Harbin, Harbin Institute of Technology Press, 2010:171-173 (in Chinese)

[19] Koji Isogai. On the Transonic-Dip Mechanism of Flutter of a Sweptback Wing[J]. AIAA Journal, 1979, 17(7):793-795

[20] Koji Isogai. Transonic Dip Mechanism of Flutter of a Sweptback Wing: Part Ⅱ[J]. AIAA Journal, 1981, 19(9): 1240-1242

[21] Alonso J, Jameson A. Fully-Implicit Time-Marching Aeroelastic Solutions[R]. AIAA-1994-0056

[22] Zhang Zhichao, Yang Shuichi, Liu Feng. Prediction of Flutter and LCO by an Euler Method on Non-Moving Cartesian Grids with Boundary-Layer Corrections[R]. AIAA-2005-833

[23] Timme S, Badcock K J. Searching for Transonic Aeroelastic Instability Using an Aerodynamic Model Hierarchy[R]. Technical Report Deliverable D2.3, UK: University of Liverpool, 2009

[24] 刘南. 机翼跨声速非线性颤振及高效分析方法研究[D]. 西安：西北工业大学，2016

Liu Nan. Investigation of Transonic Nonlinear Flutter and Efficient Analysis Approach[D]. Xi′an, Northwestern Polytechnical University, 2016 (in Chinese)

[25] Bendiksen O O. Transonic Stabilization Laws for Unsteady Aerodynamics and Flutter[R]. AIAA-2012-1718