基于粒子群优化的云计算低能耗资源调度算法

贾嘉, 慕德俊

(西北工业大学 自动化学院, 陕西 西安 710072)

随着对云计算需求的不断扩大，几大云计算服务提供商，如Amazon等，建立了越来越多的数据中心，以满足云计算对基础设施资源的需要。为了维护大规模的数据中心运行，需要大量能耗。这不仅提高了服务成本，也给相应基础设施带来巨大压力。有研究表明，数据中心的使用率一般在5%～20%[1-2]；而空闲服务器的电量消耗也超过满负荷情况下的50%。能耗是云计算成本中重要一环。针对云环境中数据中心的能耗问题，本文研究了面向低能耗的基于粒子群优化算法的数据中心资源分配算法。采用帕累托最优解集合描述所有可行的最优解。为了得到帕累托最优解集合，采用粒子群优化算法，对不同的分配方案迭代寻优，并按存活周期随机变异分配方案。通过比较不同分配方案下能耗，得到最优的资源分配方案。

1 云计算与粒子群优化

1.1 云计算概述

云计算作为一种新兴的并行计算技术，是分布式处理、并行处理、网格计算的发展和延伸。它提供了更可靠、更安全的存储和计算数据能力、简化计算交付、降低成本、具有更高的扩展性和灵活性。云计算采用计时付费的形式，程序员只需关注应用程序本身，关于集群的处理问题，则交由平台处理。云计算重要特点之一是虚拟化。虚拟化技术范畴从简单的硬件抽象逐渐发展成为虚拟云操作系统，云主机能够大量根据用户定义的服务质量(quality of service,QoS)规范执行应用程序的VMs并行分享。

1.2 粒子群优化

粒子群优化(particle swarm optimization,PSO)算法[3]是一种模拟鸟群觅食行为的演化计算算法。因其结构简单、参数少、易实现，所以受到广泛重视并被应用到了许多自然科学和工程科学领域。标准的PSO的形式如下

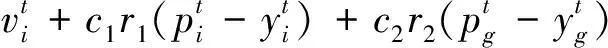
2 云计算能耗模型

云计算体系下,数据服务需要满足很多限制性条件,如相应时间、吞吐量等。对于资源调度而言,这些指标构成了调度算法的约束条件。本节首先研究了与调度相关的能耗模型,得到能耗的代价函数及约束条件;并指出,所求问题的解为帕累托最优解集合。然后采用粒子群优化算法对代价函数求取最优解集合。

2.1 能耗模型

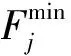
min∑mj=1∑ni=1fijxij3

(2)

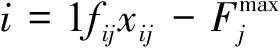
(3)

约束条件为

xij∈{0,1},i=1,2,…,n;j=1,2,…,m

(4)

∑mj=1xij=1, ∀i

(5)

(6)

∑ni=1fijxij≤maxFj, ∀j

(7)

式中,xij=1表示第i个虚拟主机调度到第j个服务器,取0则否;fij表示第i个虚拟主机在第j个服务器上占用的频率。

2个代价函数分别对应了不同的能耗指标。代价函数(2)代表了所有虚拟主机总动态功耗之和最小;代价函数(3)表示尽可能提高某一台服务器的利用率。代价函数(2)和(3)存在一定的冲突关系,从而构成一个典型的多目标优化问题。与之相关,约束条件则反应了虚拟主机与服务器的硬性关系。约束条件(4)中,xij=1表示虚拟主机i分配到服务器j上,而约束(5)表示虚拟主机只能被分配到1台服务器;约束(6)指出每个虚拟主机占用频率的上下限;约束(7)表示1台服务器上所有虚拟主机占用的频率和不能超过服务器负载。

决策变量x={xij}和f={fij}构成了最终的解。x决定了虚拟主机在服务器上的分配;而f则指出该分配下虚拟主机使用的频率大小。如前所述,代价函数(2)和(3)计算决策变量x和f是一个多目标优化问题,传统的最优化算法难以求解。本节剩余部分讨论了求解x和f的方法。

2.2 多目标优化的帕累托最优

一般而言,代价函数(2)和(3)是相互冲突的,所以不存在使二者同时达到最小的惟一解,而是产生一组解的集合。数学上,把这种没有一个解比其他解更优的最优解集合称为帕累托最优解集或帕累托最优前沿(Pareto optimal front, POF)。此时,对于(2)和(3)对应的代价函数,任意2个解f1和f2存在2种可能的关系:一个解优于另一个解,或者两者都不比对方优。

本文采用帕累托占优条件[4]来判断解之间的关系。针对(2)和(3)对应的代价函数的解f1和f2,当f1的一个代价函数严格优于f2,且另一个代价函数f1不严格劣于f2,则称f1帕累托占优f2,即当满足下式时,f1帕累托占优f2。

∀i:gi(f1)≤gi(f2)

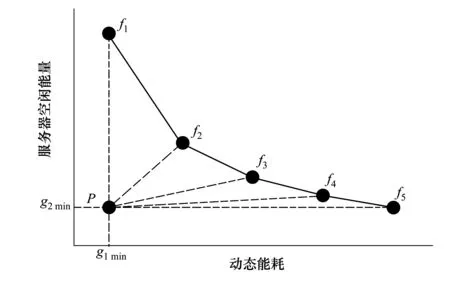
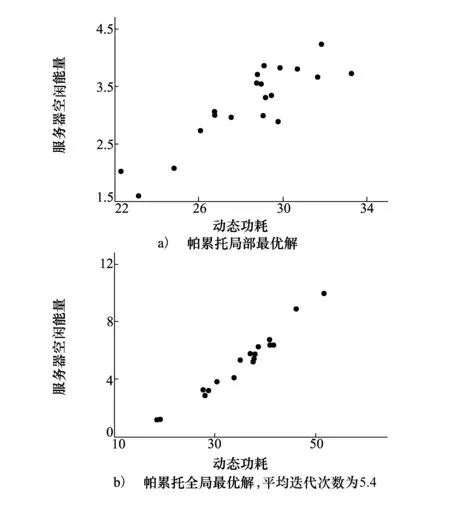
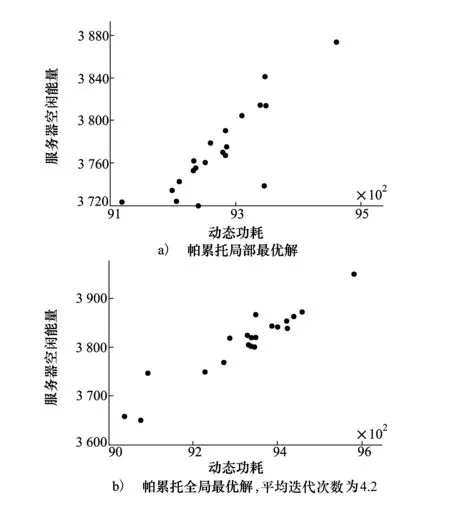
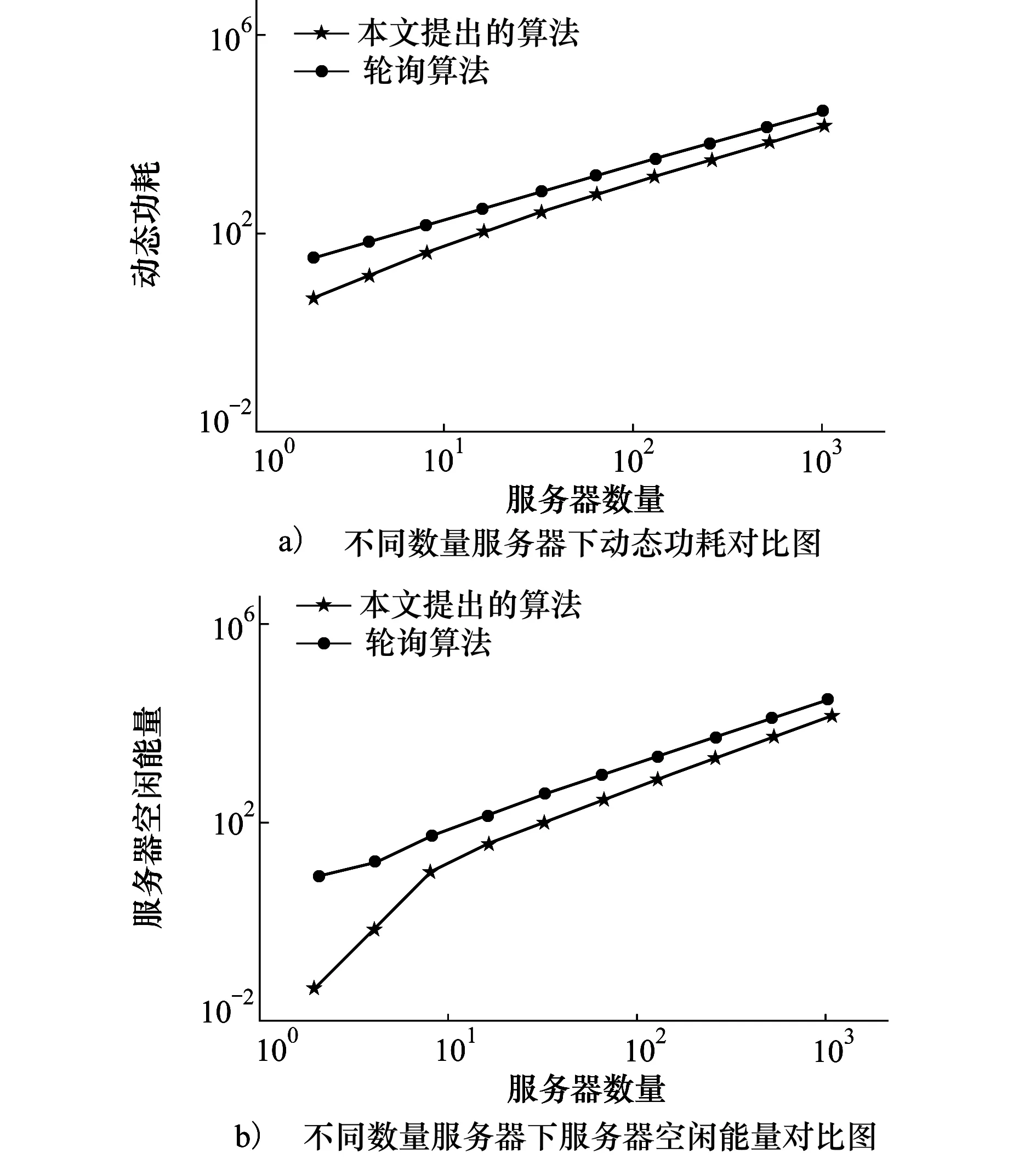
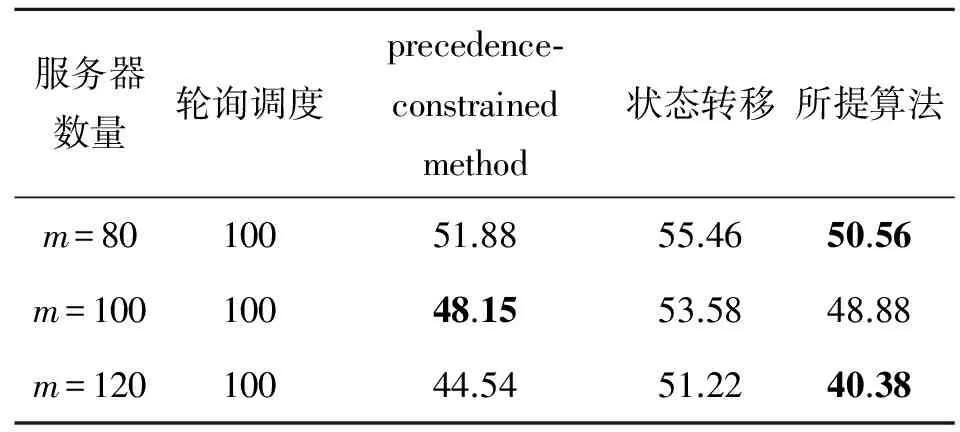
∃j:gj(f1)

(8)

式中,gi,i=1,2是代价函数(2)或(3)。在给定了一个服务器分配方案x后,由(8)可以评估任意2个频率分配方案f1和f2。

3 基于粒子群优化的低能耗资源调度算法

由第2节可知,待求的决策变量为x和f。由于需要指定一个服务器分配方案x后,才可能获取一个频率分配方案f,因此,本文首先随机给出一个分配方案x;在该方案下,使用经典的粒子群算法进行寻优,得到该方案对应的帕累托最优解集合;通过随机改变方案,得到不同方案的最优解集合,合并成为全局最优解集合,并在该集合中寻找最终解。

3.1 频率分配方案

首先随机产生一个服务器分配方案xt。在xt下,按照约束条件随机生成关于频率分配ft的粒子群y={yi}。对于每个粒子yi,按照式(1)所示的迭代过程,进行寻优。

1) 粒子群寻优。对于每一个方案,按照经典的粒子群算法(1),需要使用粒子的局部最优解pi和全局最优解pg。多目标最优情况下,每个粒子yi存在多个局部最优,进而合并所有粒子将产生多个全局最优。因此,本文算法中允许每个粒子最多产生的Nl个局部最优,即pi={pi,1,pi,2,…,pi,Nl,},而合并所有局部最优得到的全局最优集合,最多包含Ng个元素,即pg={pg,1,pg,2,…,pg,Ng}。对于多余的解,有不同的处理方法。与文献[5]不同,本文算法采用随机抛弃多余解的方法。显然,这有利于提高算法的实时性。

2) 迭代终止条件。为了停止粒子群迭代寻优,本文设计依据服务器分配方案存活时间的服务器分配方案跳转概率Px。Px具体的构造方法在3.2节讨论。发生跳转时,算法存储当前xt及其对应的全局最优解ft=pg。取遍所有可能的组合xt及其对应的ft,合并所有解得到最终的解集合x={xt}和f={ft}。

3) 3种帕累托最优解集合。本文涉及到3种不同的帕累托最优解集合,为了避免混淆,在此指明其相互关系。给定服务器分配方案xt下,最底层的集合是一个粒子yi迭代寻优过程中产生的局部最优解pi;合并局部最优解,得到所有粒子y={yi}的全局最优解集合ft=pg;对于不同的方案x={xt},所有ft将共同组成最终的解集合f={ft}。

3.2 服务器分配方案

本文采用服务器分配方案跳转概率Px来终止3.1节所述的频率分配寻优。

本文使用分配方案的存活周期为自变量,对跳转概率Px赋值。直观而言,如果对一个服务器分配方案xt已经进行了多次粒子群迭代寻优,则可以认为此时的结果已经近似达到该方案下的最优解,从而停止计算当前的xt,转而生成新的分配方案xt+1,重新进行寻优。出于以上的考虑,令

Px=I/Nt

(9)

式中,I为粒子群迭代次数;Nt为指定的参数。在3.1节所述粒子群寻优时,每次迭代初始都产生一个[0,1]内均匀分布的随机数,与Px进行比较,如果小于Px,则发生跳转。

实际中,服务器的个数一般在102～103间,本文算法随机抽取Nx个分配方案进行寻优。遍历所有Nx个服务器方案后,得到1组帕累托最优解集合f={ft}。

根据决策者不同的需要,选择最终的惟一解的方法也有所不同。本文采用类似文献[5]的方法,计算每个解到理想最优点的距离,以距离最小原则选取最终解,如图1所示。图1中,最终帕累托最优解集合存在5个解,f1,f2,…,f5。解f1的动态能耗最小,为g1min,解f5的服务器空闲能量最小,为g2min。于是,理想最优点为P点,对应坐标(g1min,g2min)。计算每个最优解到P点的距离,按照距离最小选取最终的解。图1中,f2为选取的最优解。

图1 距离评价方法

4 实验分析

本文采用Matlab模拟了云计算下服务器和虚拟主机。程序运行于1台PC机,内存1.75 GB,CPU为3.0 GHz。

4.1 参数设置

实验中,本文所提算法使用了如下的参数。粒子群中,惯性权重ω=1,学习因子c1=c2=1.5;采用20个粒子进行迭代寻优。每个粒子最多保留Nl=5个局部帕累托最优,而所有粒子共保留Ng=20个全局帕累托最优。用于生成跳转概率的Nt是关键参数,较小的Nt将使算法更快结束,而较大的Nt则增加了每个方案的迭代寻优次数,从而提高得到该方案下最优解的概率。文中取Nt=20。显然,当迭代次数n=20时,按照(9)式所示,算法必然发生跳转,因此,Nt还起到了传统粒子群算法中迭代次数最大值的作用。

4.2 不同服务器资源下对比实验

通过调整服务器数量m和虚拟主机数量n,在不同的任务类型下进行了实验。对比算法采用工业界普遍使用的轮询调度方法。

首先验证了在m=5个服务器和n=10个虚拟主机环境下算法的性能。图2显示了所提算法的调度结果。其中,图2a)显示了某个帕累托局部最优解集合,而图2b)展示了最终的所有帕累托全局最优解。按照3.2节所述距离评价方法,算法最终选择图2b)中左下点对应的决策变量作为最终解,其动态功耗为18.6 W,服务器空闲能量为1.157 W。在本实验中,每个粒子群平均存活了5.4次迭代。算法的实时性基本满足实际要求。采用轮询算法,动态功耗为80 W,服务器空闲能量为20 W。

图2 少量服务器/虚拟主机资源调度结果

在中量负载情况下,取m=100个服务器,n=300个虚拟主机,所提算法得到如图3所示结果。此时,动态功耗为1 029 W,服务器空闲能量为566.3 W。采用轮询算法,动态功耗为2 400 W,服务器空闲能量为1 600 W。在大量负载情况下,取m=1 000个服务器,n=2 500个虚拟主机,所提算法得到如图4所示结果。此时,动态功耗为9 038 W,服务器空闲能量为3 657 W。采用轮询算法,动态功耗为20 000 W,服务器空闲能量为10 000 W。

图3 中量服务器/虚拟主机资源调度结果

图4 大量服务器/虚拟主机资源调度结果

了验证所提算法对变化的服务其数量及虚拟主机数量的鲁棒性,取m={21,22,…,210}个服务器,对应虚拟主机数量n为m的21+(t-1)/10倍,t=1,2,…,10随序号依次增多。例如,当m=210时,n=3 821。由于在4.1节参数设置中已经指明,1台服务器最多可以容纳4台虚拟主机,此时n/m=3.73已经接近服务器饱和状态。图5显示了对比结果。图5a)为动态能耗对比图,图5b)为服务器空闲能量对比图。出于可视化考虑,采用了log坐标系。

图5 不同数量服务器下性能对比图

由图5可见,所提算法比轮询调度算法在动态能耗和服务器空闲能量2个指标上,均取得更优的结果。在全部10组实验上,所提算法的动态能耗均小于轮询调度的50%。

4.3 能耗优先对比实验

对比算法中,除了4.2节使用的轮询调度外,还采用了文献[6]中优先受限的(precedence-constrained)并行应用调度算法,以及文献[7]采用的状态转移算法。

设定服务器数量m={80, 100, 120},对应虚拟主机数量n={1,2,3}×m。为了直观对比各算法的能耗,将轮询调度的能耗指定为x,而其余算法的能耗相应换算为轮询调度的占比[8-9]。

表1展示了不同算法在n/m=1时的实验结果。表2对应n/m=2的结果;表3为n/m=3的结果。各表中,黑体标出了能耗最低的算法。

表1 不同算法能耗对比表,n/m=1 (%)

表2 不同算法能耗对比表,n/m=2 (%)

表3 不同算法能耗对比表,n/m=3 (%)

从表1～表3可见，轮询调度的耗能最多，且普遍为智能算法能耗的2倍以上。在3种能耗相关的智能算法中，状态转移算法的表现一般，在不同服务器/虚拟机比例下，均没有获得最少的能耗。这是由于状态转移受限于其固有的模型假设，而实际中，转移阵实时、动态的变化，往往给该算法带来极强的扰动因素，造成算法性能下降。所提算法在7组实验中取得最低的能耗。

5 结 论

针对云计算中能耗过高的问题，提出一种基于粒子群优化的资源调度算法。首先给出了能耗模型，以虚拟主机在服务器上的分配方案和占用的频率为决策指标，进行优化。指出了该模型为多目标优化问题，从而存在多个最优解，即帕累托最优解集合。采用粒子群优化算法对于每个分配方案进行迭代寻优，按照从属关系逐次构造了单粒子帕累托局部最优解集合、粒子群帕累托全局最优解集合和最终的跨分配方案的帕累托最优解集合共3个集合。在最终的集合上，采用距离评价标准，自主选择惟一的解。在不同数量的服务器和虚拟主机环境下进行了仿真实验。实验结果表明所提算法所需能耗低于轮询算法的50%。

参考文献：

[1] Ludwig Siegele. Let it Rise: A Special Report on Corporate IT[M]. Economist Newspaper, 2008

[2] Rangan Kash, Cooke A, Post J, et al. The Cloud Wars: ＄100+billion at stake[R]. Tech Rep, Merrill Lynch, 2008

[3] James Kennedy. Particle Swarm Optimization[M]. Encyclopedia of Machine Learning, Springer, 2010

[4] Abido M A. Multiobjective Particle Swarm Optimization for Environmental/Economic Dispatch Problem[J]. Electric Power Systems Research, 2009, 79(7): 1105-1113

[5] 刘静,罗先觉. 采用多目标随机黑洞粒子群优化算法的环境经济发电调度[J]. 中国电机工程学报, 2010, 30(34): 105-111

Liu Jing, Luo Xianjue. Environmental Economic Dispatching Adopting Multi-Objective Random Black-Hole Particle Swarm Optimization Algorithm[J]. Proceedings of the CSEE, 2010, 30(34): 105-111 (in Chinese)

[6] Mezmaz M, Melab N, Kessaci Y, et al. A Parallel Bi-Objective Hybrid Metaheuristic for Energy-Aware Scheduling for Cloud Computing Systems[J]. Journal of Parallel and Distributed Computing, 2011, 71(11):1497-1508

[7] Lee Young Choon, Zomaya A Y. A Novel State Transition Method for Metaheuristic-Based Scheduling in Heterogeneous Computing Systems[J]. IEEE Trans on Parallel and Distributed Systems, 2008, 19(9): 1215-1223

[8] Li Y, Chen M, Dai W, Qiu M. Energy Optimization with Dynamic Task Scheduling Mobile Cloud Computing[J]. IEEE Systems Journal, 2017, 11(1): 96-105

[9] Rimal B P, Maier M. Workflow Scheduling in Multi-Tenant Cloud Computing Environments[J]. IEEE Trans on Parallel and Distributed Systems, 2017, 28(1): 290-304