改进遗传算法在供热系统中的应用

张京杰，姜丽芬，花季伟，张少强

（天津师范大学计算机与信息工程学院，天津300387）

遗传算法因其自身优势已经在科学研究的许多领域有广泛的应用.Stephen Smith、Nichael Crumb以及Jhon Koza等学者先后各自独立阐述了遗传编程的概念，即自动化生成和选择计算机程序来完成用户定义的任务[1].国内学者在遗传算法研究领域也取得了一些研究成果.如，文献[2]提出了基因块编码的概念，并结合并行遗传算法的框架，在群体中识别出优势基因块作为下一轮重复操作的初始群体.文献[3]提出针对并行遗传算法求解TSP问题，探讨了使用弹性策略来维持群体的多样性，使得算法跨过局部收敛的障碍，向全局最优解方向进化.

集中供热是当前社会关注度比较高的民生问题.解决供热网中供热冷热不均问题的常用方法，是将该问题抽象为一个函数优化问题，通过函数抽象，利用相关算法调节供热网中水流量来解决.文献[4]针对换热站质调、量调通道之间的耦合作用和控制模型参数时变的问题，利用模糊控制器对PID参数进行优化.文献[5]使用了基于蚁群优化的遗传算法对PID参数进行整定，降低了超调量，但整定时间较长.本文提出一种改进的遗传算法.算法的选择运算采用精英策略；交叉运算采用可调节的交叉概率，使得不同的个体采用不同的交叉概率，确保适应度高的个体获得较低的交叉概率，从而有更大机会复制到下一代中；变异运算采用集中程度的概念分析数据，对应不同的情况调整算法的变异概率，变异概率的改进可以避免群体过早收敛，并且可尽快找到问题的最优解.

1 供热系统中温控系统数学模型

实施城市集中供热的主要目的就是提高室内温度，创造一个适合人们正常生活工作和生产的室内温度环境，所以，衡量供热品质的最重要标准就是供热后的室内温度[6-7].

目前，我国供热技术自动控制方面仍有不足，在现有资源供给有限的条件下，仅仅利用以往的经验，通过人工控制调节供热系统，已经满足不了人们的需求.因此，智能化操作便成了大势所趋，结合计算机监控技术实现整个供热系统的数据采集管理，运行状况分析，研究建立网络化热网监控系统控制，使其控制系统更加科学有效，显得极为重要[8].

换热站是集中供热控制系统中的重要组成部分.换热站的运行程序独立存在于控制系统PLC中，其可以通过控制上位机监控管理系统进行观察并实施调整.换热站温度控制系统根据室外温度的变化给二次侧热网供水温度分别设置各自对应的设定值，实现不同的室外温度下二次侧供水温度的恒定.温度控制系统通过比较二次网侧供水温度和设定值计算出电动调节阀的开度作为输出值来控制换热站的一次供水流量.换热站供热系统如图1所示.

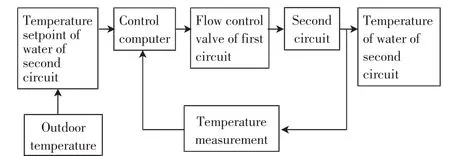
图1 换热站供热系统图Fig.1 Heating system of heat exchange station

换热站一次侧传递热量Q1为

其中：Q1为单位时间内一次侧传递给管壁L1的热量，单位W；c1为水的比热容，单位J/（kg·℃）；q1为L1的水流量，单位kg/s；T1g为L1供水温度，单位℃；T1h为L1回水温度，单位℃.

换热站二次侧传递热量Q2为

其中：Q2为单位时间内一次侧传递给管壁L2的热量，单位W；c2为水的比热容，单位J/（kg·℃）；q2为L2的水流量，单位kg/s；T2g为L2供水温度，单位℃；T2h为L2回水温度，单位℃.

换热站两侧传热速率方程为

其中：Q3为在单位时间内管壁L1至管壁L2的传热量，单位W；U为传热系数，单位W/（m2·℃）；A为换热站的换热面积，单位m2.

对于一次侧管网，有

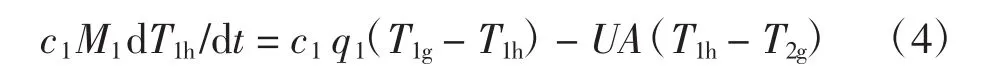
对于二次侧管网，有

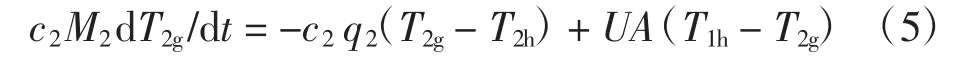
其中：M1为单位时间内一次侧积存的水量，M2为单位时间内二次侧积存的水量，单位均为kg/s.

设T1g－T1h=Δt1为常数，式（4）可线性为

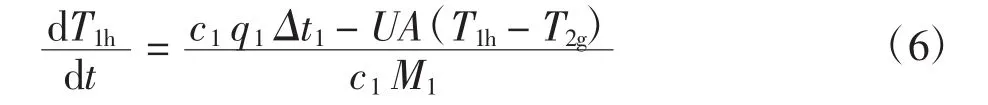
由于所有温度都是基于L2回温，即T2h的偏差，故式（5）可变为

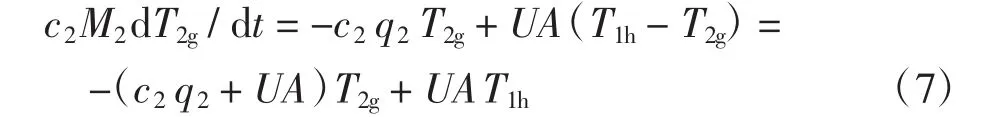
求导得

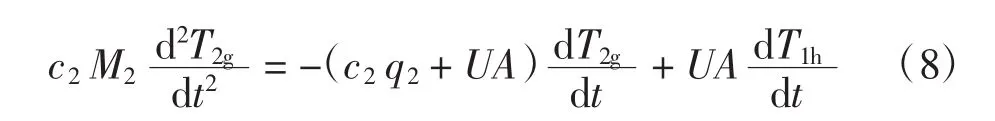
将式（6）代入式（8）得

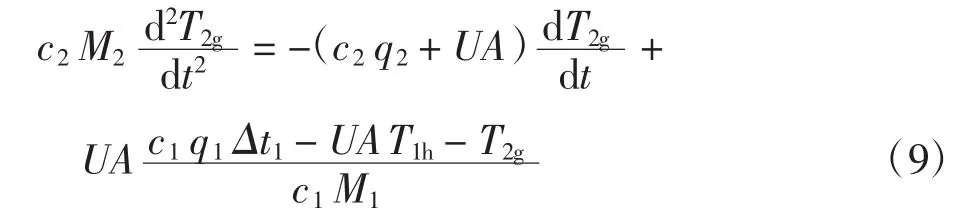
由式（7）得

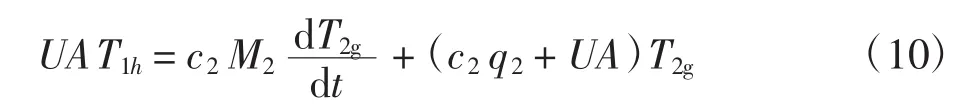
综合式（9）和式（8）得

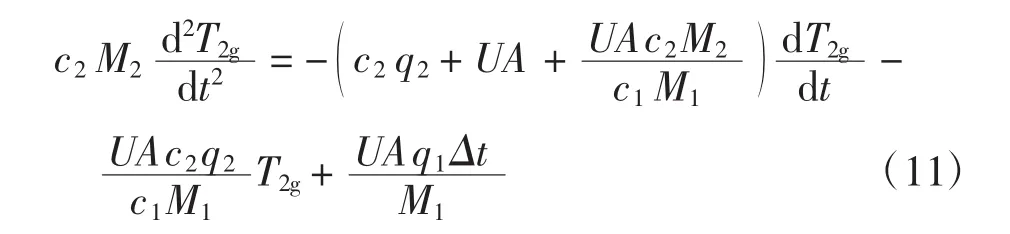
经拉格朗日式化简得

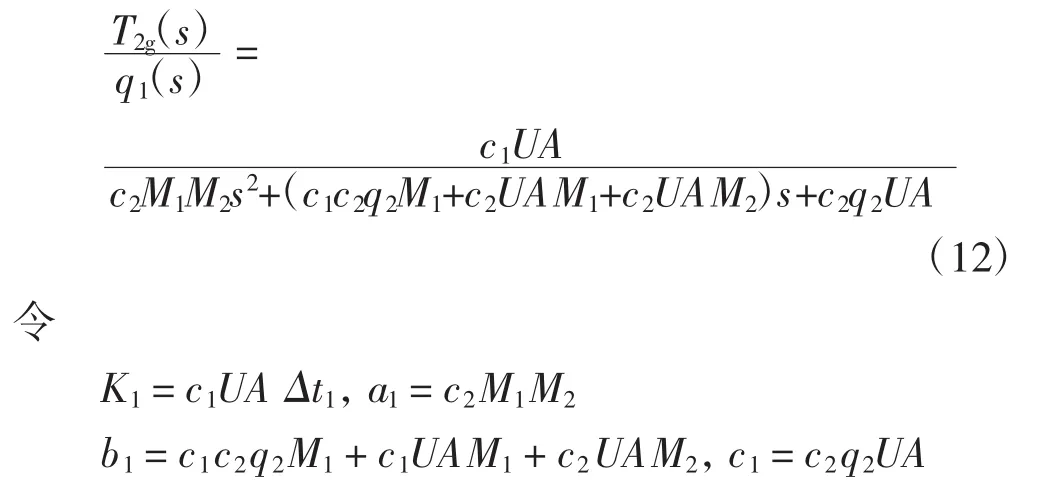
考虑到延时问题，最终得到温控系统的传递函数为

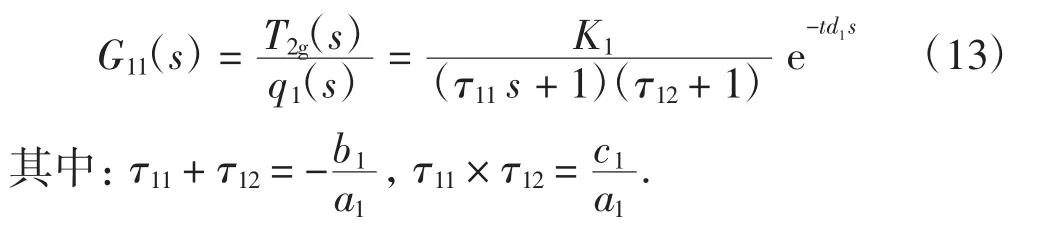
2 改进的遗传算法

杂交概率和变异概率的确定是遗传算法的关键.杂交概率和变异概率的取值对寻优速度有着重要影响，如果取值恰当，经过几代就能找到满意解；否则，经过几十代，甚至上百代的计算，目标函数值都无明显改善[9].

2.1 选择算子

改进遗传算法的精英个体是指当代中适应度最高的个体.基于精英策略的选择算子可以避免“精英”在接下来的操作中被破坏，保证将每一代中的最优解原封不动的复制到下一代中.精英策略可使算法收敛速度变快.而精英个体的数量也会影响到遗传算法的求解速度，合适数量的精英个体有利于算法的求解，设定过多的精英会造成算法局部收敛，不利于问题最优解的获得.

改进遗传算法的选择算子具体操作是，从当前代中选择2个适应度最高的个体直接进入下一代.具体实现是通过遍历找到当代适应度最高的个体保留.

2.2 交叉算子

基本遗传算法中的交叉概率设置后，在算法的不同阶段都是不变的，这不利于实际问题的解决.本文中的交叉概率能够根据问题具体调整，以便较快找到问题的最优解.

设计交叉概率如下：

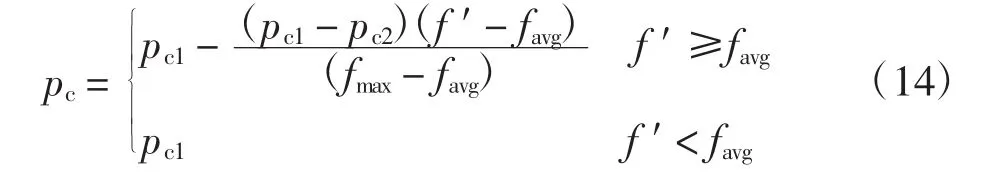
其中：pc1=0.9，pc2=0.6；fmax为群体中的最大适应度值；favg为每代群体平均适应度值；f′为个体适应度值.由式（14）可以看出，当个体适应度大于或等于适应度的平均值时，交差概率较低；当个体适应度值小于平均值时，则交叉概率变高.这样，适应度值越高的个体越容易保留到下一代，适应度值差的个体更大可能地进行交叉操作.

2.3 变异算子

考虑到供热系统的数据范围，定义种群的集中程度m，用于描述种群的离散趋势，

其中：fmax为当代个体中适应度最高值；fmin为当代个体中适应度最低值；favg为当代群体适应度的平均值.m越大，则种群的分布越集中，种群的进化趋于成熟，应采取较低的变异概率.m越小，则种群的分布越分散，种群的进化处于较低级阶段，应采取较高的变异概率.自适应变异概率为

根据pm进行变异，其中：pmmax为变异概率的最大值；t为当前代数；T为终止代数.

3 改进遗传算法在PID控制器上的应用

比例、积分和微分控制简称PID控制.与其他简单的控制运算不同，PID控制可以根据历史数据和差别的出现率来调整输入值，这样可以使系统更加准确和稳定[10-11].

PID控制在换热站的温度控制系统中有着至关重要的作用.当整个换热系统的运行状况发生很大变化时，固定参数的控制效果就会发生改变，使整个系统运行质量下降，有时甚至会使系统运行状态脱离安全稳定范围，这时就需要调整相应参数[12].

3.1 基于遗传算法PID控制器结构设计

PID控制器的控制效果取决于控制器的3个参数（比例因子Kp，积分因子Ki，微分因子Kd）是否合理.因此，应首先确定参数初始值的变化范围，然后利用遗传操作进行参数整定，对PID参数进行修改，再进行PID控制，PID控制器结构如图2所示.

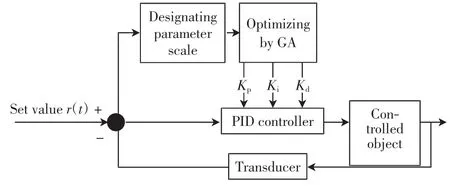
图2 遗传算法控制PID控制器Fig.2 PID controller by genetic algorithm

（1）参数的编码：首先对控制器的Kp0、Ki0、Kd0进行浮点数编码.

（2）参数变化范围的确定：为了更合理地选择参数搜索范围，首先采用Z-N整定法获得初始值Kp0、Ki0、Kd0，再以该初始值为中心向左右两边扩展，得到参数的搜索范围.

以启动时刻为例，确定参数的变化范围是Kp0=[0，5]，Ki0=[0，10]，Kd0=[0，1].

3.2 改进遗传算法实现

（1）初始种群的产生

根据参数选择范围随机产生初始种群，其主要代码如下：

（2）适应度函数选择和计算

适应度函数的主要代码如下：

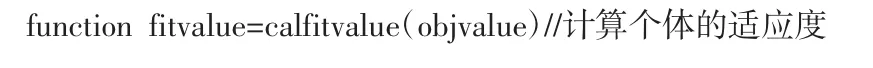
（3）选择算子的代码实现

合格的师资队伍是口腔专业研究生规范化培训的基础。建立完善的师资培训制度，在整个教学体系的标准化运行中具有重要作用，因此师资培训应规范化、制度化。每年定期组织规范化师资培训，并对师资队伍进行定期考核，不断强化教员的教学水平；在保证教学质量的同时，也要确保教员的数量。对口腔专业研究生的培训可采取专人带教、小组带教，或科室领导、教学组长、带教老师三级综合带教模式；同建立带教教员的评估和监察制度，确保规范培训的教学质量。

首先找到适应度最大的个体.

引入精英策略的选择操作.

（4）交叉算子

按照适者生存的原则，不同的个体采用不同的交叉概率，保证适应度高的个体获得较低的交叉概率.

（5）变异算子

根据每一代的聚合程度，设置变异概率，主要代码如下：

4 改进遗传算法及其MATLAB仿真

4.1 改进遗传算法最优解仿真

测试程序采用了Rosenbrock函数作为测试函数，该函数有2个局部极值f（2.048，-2.048）=3 897.734 2和f（-2.048，-2.048）=3 905.926，后者为该函数全局最大值点.设定pc=0.9，pm=0.08，T=600.仿真结果见图3和图4.

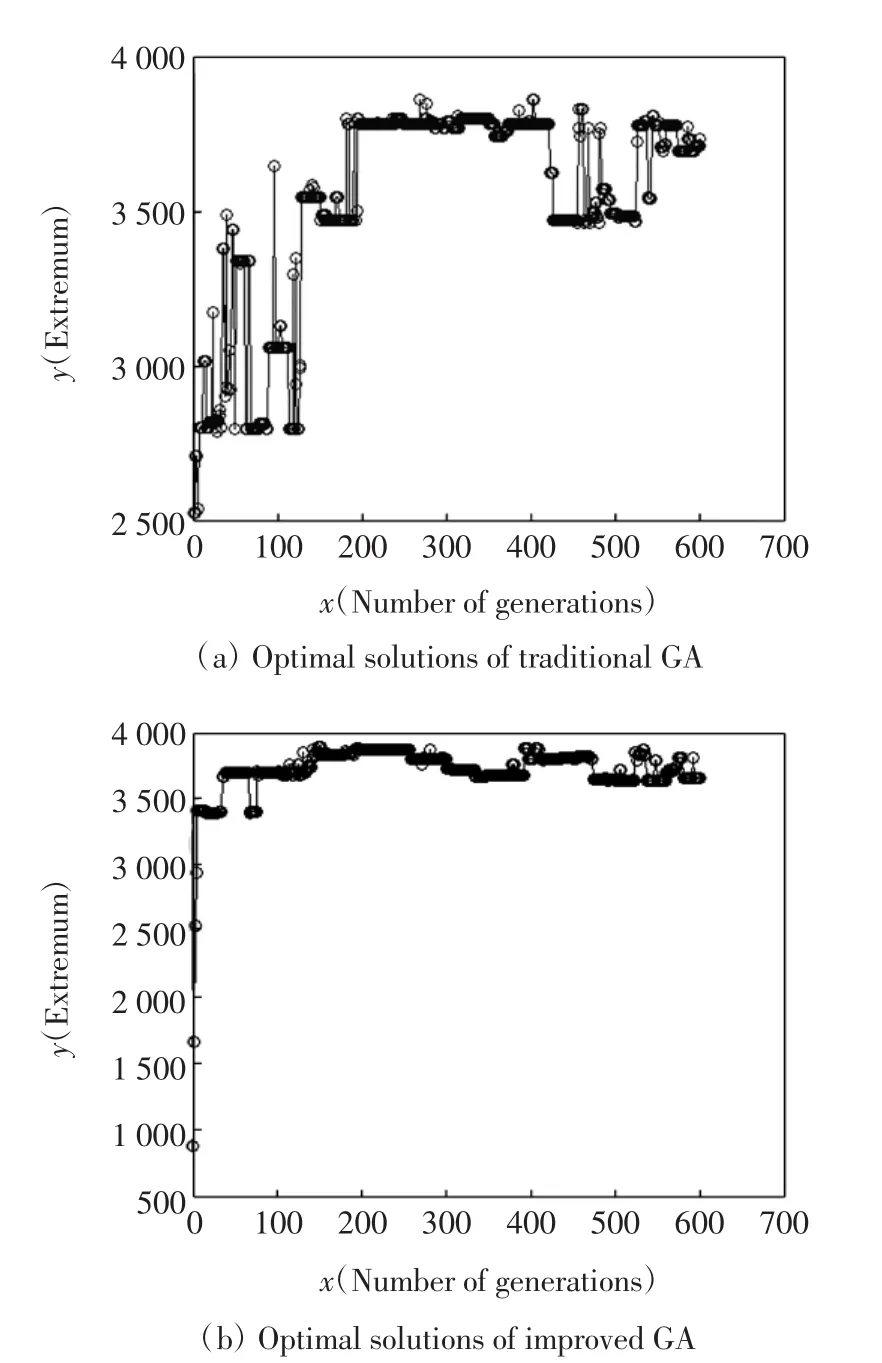
图3 一次求解对比图Fig.3 Diagrams of primary solutions

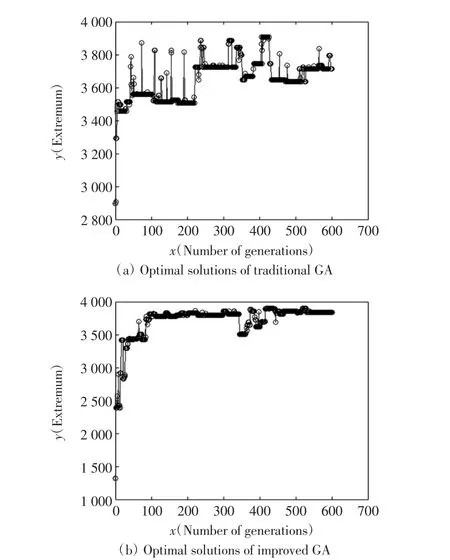
图4 二次求解对比图Fig.4 Diagrams of secondary solutions

图3（a）和图4（a）为传统遗传算法在运行过程中求最优解的情况.图 3（b）和图 4（b）为改进遗传算法求最优解的情况.可以看出，传统遗传算法最优解曲线呈现出震荡、不平稳的状态，而改进遗传算法的解曲线能快速收敛到最优解，而且寻找到最优解的准确性较高.实验结果表明，本文所提出的遗传算法相对于传统遗传算法，收敛速度和求解速度均较快.

4.2 改进遗传算法PID控制器和常规PID控制器的MATLAB仿真

给定二次网供水温度参考平均温度为50℃，检测时间范围为0～500 s，滞后时间为190 s，对常规PID控制和应用改进遗传算法的PID控制进行了仿真，仿真结果见图5和图6.

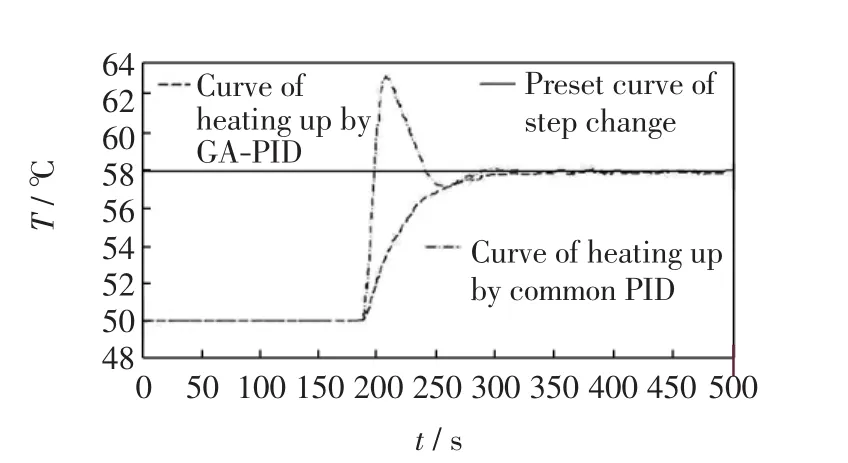
图5 升温曲线图Fig.5 Curves of heating up

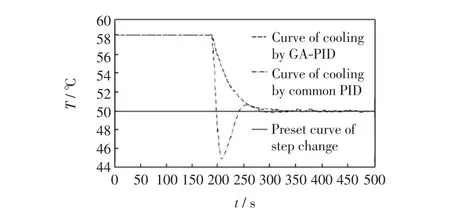
图6 降温曲线图Fig.6 Curves of cooling

当室外温度降低，二次网供水温度应相应升高，常规PID控制器和应用改进遗传算法的PID控制器调节情况如图5所示.当室外温度升高，二次网供水温度应相应降低，常规PID控制器和应用改进遗传算法的PID控制器调节情况如图6所示.从图5和图6可以看出，常规PID控制器响应曲线超调量较大，而应用改进遗传算法的PID控制器实现了超调量小的效果.实验结果表明，采用改进遗传算法的PID控制器使控制系统更加准确，系统具有进入稳态平稳、无振荡、控制精度高等特点.

5 结论

本文提出一种改进的遗传算法，该遗传算法的选择运算采用了精英策略；交叉运算应用了自适应法则；变异运算采用了集中程度的概念，对应不同的情况调整变异概率.在MATLAB中实现了改进遗传算法与传统遗传算法的求解对比实验，以及改进遗传算法PID控制器仿真实验.实验表明：相对于传统算法，改进遗传算法具有更高的收敛速度和求解效率；将改进的遗传算法应用到换热站控制系统的PID控制器上，可以使控制系统有更高的控制精度，其动态性能和鲁棒性均比较理想.

参考文献：

[1] HOLLAND J.Adaptation in natural and artificial systems：An introductory analysis with applications to biology[J].Control and Artificial Intelligence，1975，6（2）：126-137.

[2] 赵宏立，庞小红，吴智铭.基因块编码的并行遗传算法及其在TSP中的应用[J].上海交通大学报，2004，38（1）：213-217.ZHONG H L，PANG X H，WU Z M.A building block coded parallel genetic algorithm and its application in TSP[J].Journal of Shanghai Jiaotong University，2004，38（1）：213-217（in Chinese）.

[3] 江雷，陈贤富.基于遗传算法的弹性TSP研究[J].计算机应用，2004，24（7）：40-42.JIANG L，CHEN X F.Study of elastic TSP based on genetic algorithm[J].Journal of Computer Applications，2004，24（7）：40-42（in Chinese）.

[4] 徐澎波，王伟杰，黄晓童.采用神经网络：模糊PID的换热站控制器设计与仿真[J].节能技术，2012，30（3）：224-228.YU P B，WANG W J，HUANG X T.Design and simulation of heat substation controller based on neural network-fuzzy PID control[J].Energy Conservation Technology，2012，30（3）：224-228（in Chinese）.

[5] 殷文雪，朱栋华，孟显娇，等.基于蚁群优化的遗传算法在集中供热系统中的应用与仿真[J].电子世界，2014（16）：331-332.YIN W X，ZHU D H，MENG X J，et al.Application and simulation of genetic algorithm based on ant colony optimization in centralized heating system[J].Electronics World，2014（16）：331-332（in Chinese）.

[6] 黄文，管昌生.城市集中供热研究现状及发展趋势[J].国外建材科技，2004，25（5）：77-79.HUANG W，GUANG C S.Research status and development trend on urban centralizedheating[J].ScienceandTechnology of Overseas Building Materials，2004，25（5）：77-79（in Chinese）.

[7] 杜远辉.基于改进遗传算法的地区电网无功规划优化[D].济南：山东大学，2006.DU Y H.Reactive Power Planning Optimization in Area Power Network Based on Improved Genetic Algorithm[D].Jinan：Shandong University，2006（in Chinese）.

[8] 刘楠.换热站温控系统控制算法优化及远程监控系统设计[D].天津：天津理工大学，2013.LIU N.Design of Remote Monitoring System and Algorithm Optimization for Temperature Control System of Heat Exchange Station[D].Tianjin：Tianjin University of Technology，2013（in Chinese）.

[9]严韬，陈建文，鲍拯，等.基于改进遗传算法的天波超视距雷达二维阵列稀疏优化设计[J].电子与信息学报，2014，36（12）：3014-3020.YAN T，CHEN J W，BAO Z，et al.Optimization design of sparse 2-D arrays for over-the-horizon radar（OTHR）based on improved genetic algorithm[J].Journal of Electronics and Information Technology，2014，36（12）：3014-3020（in Chinese）.

[10]李志坚，吴晓军，任哲坡，等.基于分布式粗粒度并行计算的遗传规划算法研究[J].计算机应用研究，2015，32（1）：48-50.LI Z J，WU X J，REN Z B，et al.Research of genetic programming based on distributed coarse-grained parallel computing[J].Application Research of Computers，2015，32（1）：48-50（in Chinese）.

[11]殷雅冰.热力网远程测控系统设计[J].河北工业大学学报，2012，41（5）：27-31.YIN Y B.Design of remote measurement and control system of heat network[J].Journal of Hebei University of Technology，2012，41（5）：27-31（in Chinese）.

[12]曲志坚，张先伟，曹雁锋，等.基于自适应机制的遗传算法研究[J].计算机应用研究，2015，32（11）：3222-3225.QU Z J，ZHANG X W，CAO Y F，et al.Research on genetic algorithm based on adaptive mechanism[J].Application Research of Computers，2015，32（11）：3222-3225（in Chinese）.