不同重力环境下间隙铰链关节磨损分析

屈盛官，段 勇，赖福强，杨 超，李小强

(华南理工大学机械与汽车工程学院,广州 510640)

0 引 言

随着我国航天事业的快速发展，越来越多种类的空间机构被逐步用于空间探索实践。间隙铰链关节作为空间机构实现各种运动功能的基本构件，是空间机构重要的组成部分，其性能将直接影响空间机构的寿命和可靠性，如航天器上的太阳能电池板、空间机械臂以及空间大型天线等，铰链关节都是其基本的活动连接器[1-3]。研究表明，许多空间机构部件的故障与失效均与活动部件的磨损有关[4]。

通常对于间隙铰接副一般会采用不定期注入润滑脂或者首次集中润滑的方式，以保证其具有良好的润滑状态。而空间机构在轨服务时，空间环境将对活动部件的磨损产生严重的影响，由于空间环境非常复杂和恶劣，造成润滑脂的更新不到位，使得间隙铰链关节大多处于不良的润滑状态，导致铰接副出现过度磨损等现象。因此，对此类在没有良好润滑情况下的空间间隙铰链副进行磨损计算，对于航天器的设计具有重要的指导意义。

目前国内外对于间隙铰链关节的干摩擦进行了广泛的研究，并且取得了较多的研究成果。比如，Flores[5]对间隙铰接副的磨损与多体系统动力学的融合进行了详细的阐述；文献[6-7]采用基于Archard磨损模型的有限元方法对含间隙铰接运动副的曲柄滑块机构进行了研究，预测了间隙铰接关节的磨损特性，并通过试验进行了验证；Su等[8]将有限元方法与含间隙机构运动学相结合，并基于Archard磨损模型，对含间隙铰磨损进行了分析；宿月文等[9]基于有限元方法，建立了铰接副磨损与系统动力学行为耦合的数值分析模型，预测了刚体系统中间隙铰接副的磨损；朱爱斌等[10]将非对称Winkler弹性基础模型求解得到铰接副间的接触压力的分布，采用Archard磨损模型计算接触表面的磨损量，并对间隙铰接副的磨损进行了预测。但以上文献在采用Archard磨损模型计算接触表面的磨损量时，并没有考虑磨损过程中接触面积的变化对磨损过程的影响。特别是在磨损初期，由于磨损速率较快，使得接触面积增加，导致接触压强减小，对磨损过程有较大的影响。而且目前对于重力作用对间隙关节磨损影响的探究也很少。由于空间机构的装配和调试均在地面进行，当机构在空间环境中服役时，重力释放所引起的机构运动行为的变化会导致运动副间磨损情况的改变。因此，研究重力效应对空间机构及活动件磨损的影响，探究不同重力环境下间隙关节的磨损机理，对解决各类复杂航天器系统长期有效服役问题，以及我国航天事业在空间机构领域的工程应用、技术完善与理论发展具有十分重要的意义。

本文以含间隙铰接副的多体系统为对象，从机械系统摩损与动力学行为耦合作用的角度，研究不同重力环境对间隙铰接副的磨损特性的影响。并采用基于Archard磨损模型二次开发的ANSYS程序来仿真磨损过程，考虑了磨损过程中接触面积的变化对磨损过程的影响。

1 间隙旋转关节的多体动力学建模

1.1 间隙的定义

机械系统运动关节的间隙对于连接部件的相对运动是必须的，但是这些间隙将会影响系统的动态响应，最终导致实际结果与预期的差异，同时产生不必要的振动和磨损。图1为一个间隙旋转关节的示意图，间隙值的大小由轴与轴承的半径大小决定，其表达式为

c=RB-RJ

(1)

式中：RB和RJ分别为轴承和轴的半径。

1.2 间隙旋转关节的数学模型

图2为轴与轴承的接触碰撞模型示意图。Oi，Oj为轴与轴承的中心，ri，rj为轴与轴承在总坐标系下的位置矢量，则轴与轴承的偏心矢量为

(2)

并由图2可知,轴与轴承的偏心距大小eij为

(3)

则碰撞的法向矢量n为

(4)

由于碰撞引起的接触变形的表达式为

δ=eij-c

(5)

式中：c为初始半径间隙，其值为常数，由式(1)确定。因此可以用δ来判定轴与轴承是否接触，其表达式为

(6)

当δ>0时，轴与轴承发生接触碰撞并产生弹性变形，变形量为δ。

1.3 间隙运动副的接触碰撞力模型

当轴与轴承发生接触时，将产生接触碰撞力，并根据非线性赫兹力模型和库仑摩擦力模型计算，其表达式为[11-12]

F=FN+FT

(7)

式中：FN为法向接触力，FT为切向摩擦力，如图2所示。

1.3.1法向碰撞接触力计算模型

采用非线性等效弹簧阻尼模型来计算间隙法向碰撞接触力，其由两构件之间的相互切入而产生的弹性力和相对速度产生的阻尼力两部分组成，法向接触力大小FN的表达式为

(8)

1.3.2摩擦力模型

本文考虑间隙关节处为干摩擦，并且使用了修正的Coulomb摩擦力模型来表示轴与轴承之间的摩擦特性。该模型中的摩擦系数为动态摩擦系数，是切向滑动速度的函数，如图3所示。切向摩擦力大小的表达式为[13]

(9)

式中：μ(υt)为关于剪切滑移速度的函数，其表达式为

(10)

式中：υt为轴与轴承碰撞点的相对滑移速度，μs为静摩擦系数，μd为动摩擦系数,υs为静摩擦最大时的临界速度,υd为动摩擦最大时的临界速度。

1.4 含间隙机械臂系统动力学方程

建立机械臂动力学模型必须考虑关节间隙，关节间隙使得关节连接部件产生不同的运动特性，如自由运动和接触碰撞。因此，具有间隙关节的机械臂系统是可变拓扑系统。对于自由运动阶段，机械臂的动力学方程如下

(11)

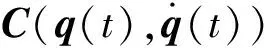
在碰撞和连续接触阶段，关节中轴和轴承之间会产生接触力。因此，动力学方程如下

(12)

2 间隙铰链关节的磨损模型

2.1 磨损模型

关于摩擦和磨损方面的模型目前有300多种以上，但是大多数模型只是仅仅针对一些特定的情况[14]。在空间环境中，黏着磨损是运动关节之间的主要磨损类型[15]。目前主要有两种研究黏着磨损的模型在摩擦学中被广泛运用，即Reye′s hypothesis模型[16]和Archard模型[17]。Archard磨损模型[6-10,16-17,19]是目前国内外学者们最常用的磨损计算公式，其计算结果较为准确。Archard磨损模型的表达式为

(13)

式中：V为磨损体积，s滑移距离，K为无量纲磨损系数，FN为法向碰撞力，H为较软材料的硬度。

假设接触区域为粗糙的表面，由于局部应力集中，在粗糙的接触峰上将发生塑性变形，则实际接触面积同法向力成正比，式(13)可以表示为

(14)

式中：Aα为实际接触面积。将式(14)左右同时除以Aα,结果为

(15)

式中：h表示磨损深度，在实际工程应用中比磨损体积更实用，可以看到磨损深度与接触压强分布有关。由于h/s表示任意时刻的磨损率，所以式(15)可以表示为

(16)

式中：K为无量纲磨损系数，p表示接触压强，H为较软材料的硬度。

有限元方法可实现对接触问题求解，通过基于Archard磨损模型二次开发的ANSYS程序来仿真磨损过程，当接触点的磨损量超过其所在单元高度的一定比例后，ANSYS便自动更新网格，重新定位边界节点[18]，如图4所示。所以磨损过程可以理解为动态过程，所以式(16)可以表示为

hj+1=hj+Δhj

(17)

式中：hj+1为到j+1步的总的磨损深度,hj为到j步的总磨损深度,Δhj为第j+1步的磨损深度，即当前步的磨损深度。

计算关节磨损时可将轴承沿接触表面展开并离散为有限个数的小区间，且每个小区间磨损均匀[8]。使轴沿着轴承展开方向滑移一次，代表轴承关节旋转一圈。将滑移速率、接触压力(取每个区间的平均接触压力)、磨损系数等参数在程序中设定便可进行轴承磨损的仿真计算。磨损前后的接触压强变化如图5所示

2.2 间隙关节的磨损耦合计算模型

磨损与动力学耦合计算流程如图6所示。首先，加载不同大小的重力载荷进行多体系统动力学分析，以确定不同重力载荷下轴承的接触压力分布，并且假设所有部件都是刚性的。在下一阶段，利用轴承的接触压力在ANSYS中得到接触压强和运用选取的磨损系数计算关节磨损。由于在机构的单个运转周期内ΔTi,磨损量极小,其对机构动力学特性参数的影响可忽略不计。所以在包含有限个运转周期NΔTi的时段内,可假设机构动力学特性保持不变,通过磨损计算程序可得到此N周期内轴承每个区间总的磨损量hj。然后将NΔTi作为磨损和动力学行为的耦合数值分析的迭代步长,并且以此阶段的每个区间的总磨损量hj对轴承的结构尺寸进行更新，并进行下一步的动力学耦合分析循环。

3 结果与分析

图7为空间机械臂系统的动力学模型，由两个灵活的机械关节组成，关节1连接臂1与航天器本体，视为不含间隙的理想铰链关节。关节2连接臂1与臂2，为间隙铰链关节。其中间隙铰链关节的尺寸和材料性能参数见表1，且臂2的初始位置为水平方向，轴与轴承的初始位置在同一轴线上。

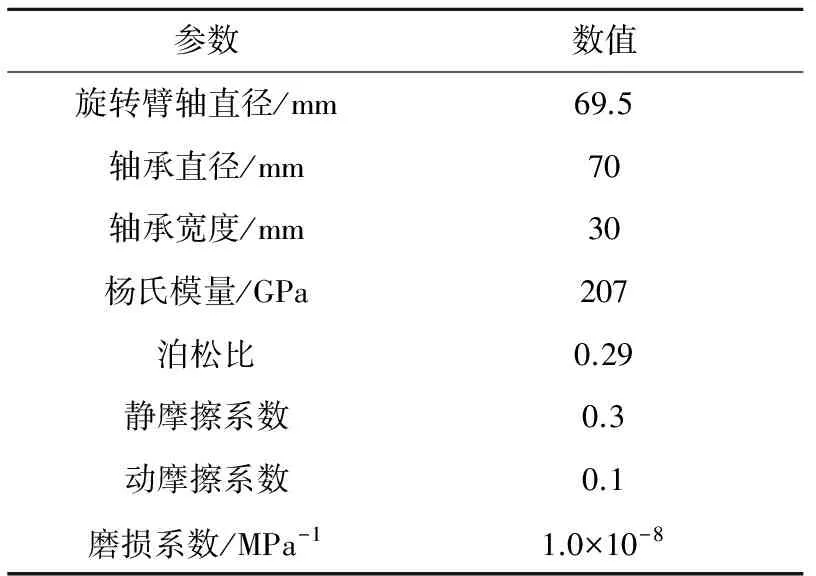
表1 模型的几何和材料性能Table 1 Dimensions and material properties of mechanism

间隙运动副采用恒转速驱动，动力学分析计算的初始状态设置为轴与轴承的中心重合,且机械臂的初始位置为水平方向。应用前文所介绍的磨损与动力学行为耦合计算流程,来分析计算间隙运动副的磨损程度和磨损间隙量。其中磨损系数通过实验得出，此处用于执行数值模拟的磨损系数选取于最佳公布的实验数据[19]。为了更好地探究不同重力环境对机械臂系统间隙运动副磨损情况的影响，使机械臂做圆周运动，并对间隙做了放大处理，使轴与轴承的配合间隙为0.25 mm。

图8(a)～图8(c)分别为转速为2π rad/s,6π rad/s,10π rad/s时不同重力环境下的初始轴心轨迹。由图8可知，在微重力环境中，当机构运行稳定后，轴的运动轨迹都趋于轴承内壁，轴与轴承始终处于连续接触状态，这必然使得轴承的磨损沿着轴承圆周分布。

在重力环境中，当转速为2π rad/s时，系统运行稳定后，销轴的运动轨迹集中在靠近轴承底端附近的位置，由于轴与轴承之间连续接触碰撞而产生的连续接触变形较大，必然会导致轴承在此区间磨损加剧；当转速为6π rad/s时，系统运行稳定后，使得轴的运动轨迹沿着整个轴承圆周分布，但是由于重力的影响使得轴心轨迹向下偏移，与轴承下部的接触变形量较大，与轴承上部的接触变形量较小，这将使得轴承下部的磨损比上部的磨损更加严重；当转速为10π rad/s时，虽然在重力环境中，轴心的运动轨迹仍向下偏移，但是变形量相对于速度6π rad/s时很小，轴心的运动轨迹和微重力环境中的基本一致，此时重力对轴承磨损的影响将减小。

在0.5g重力环境中，转速分别为2π rad/s，6π rad/s，10π rad/s时可以看到，不同速度时，轴心轨迹的分布范围和引起的轴承接触变形量都处于微重力环境和重力环境之间。可见，重力作用的减弱使得轴承的磨损分布和磨损程度有向微重力环境靠近的趋势。

原因如下：在微重力环境中，轴主要受离心力作用，所以轴的运动轨迹将沿着轴承圆周分布。在重力环境中，轴主要受离心力和重力的共同作用。当轴沿着轴承圆周运动时，由于重力始终垂直向下，使得轴承下部所受的力因重力而增强，轴承上部所受的力因重力而减弱。经计算，当转速为4π rad/s左右时，离心力大小刚好等于重力。当转速为2π rad/s时，此时离心力只有重力的0.25倍左右，不足以克服重力，所以在重力环境中销轴的运动轨迹只集中在靠近轴承底端附近的位置，且底部变形量相对于微重力环境中大很多。当重力大小减小一半时，离心力是此时所受重力的0.5倍左右，所以此时轴心轨迹分布区间增大，且由于所受重力作用减小，轴承受力也相应减小，所以底部变形量减小；当转速为6π rad/s时，离心力为重力的2.25倍左右，大于重力，但差距并不是很大，在重力环境中轴的运动轨迹沿着整个轴承圆周分布，且轴承下部所受的力因重力而增强，轴承上部所受的力因重力而减弱，所以轴承下部的变形量相对于微重力环境中变大，轴承上部的变形量相对于微重力环境变小。当重力减小时，重力的影响也会相应的减小；当转速为10π rad/s时，离心力为重力的6.25倍左右，此时重力相比于离心力很小，所以重力的影响效果减弱，当重力减小一半时，影响更小。

按照第2.1节磨损模型中的理论方法将轴承离散为36个区间，图9(a)，图9(b)，图9(c)分别为不同转速下机械臂旋转3.2×103圈后轴承圆周表面不同区间的累积磨损深度。

从图9(a)可以看出，当机械臂转速相对较低时即转速为2π rad/s，轴承的磨损分布区间和磨损程度有很大的不同。在微重力环境中轴承的磨损沿着轴承内壁相对均匀分布，且磨损程度较低；在重力环境中轴承出现集中磨损现象，磨损区域主要集中在230°～280°区间，且磨损严重，在此区间的磨损深度是微重力环境下的20倍左右，这是由于在低速时，轴所受的离心力小，重力使得轴与轴承在此区间的反复接触碰撞造成的；在0.5g重力环境中，磨损区域主要集中在210°～290°区间，由于轴承的磨损区间增大，且所受重力减小，所以轴承在此磨损区间的深度只有微重力环境下的8倍左右。结合其对应的轨迹图8(a)可知，在此速度下，重力对轴承磨损分布和磨损程度的影响都很大。

当机械臂的旋转速度为6π rad/s时，从图9(b)可以看出，由于转速增加，轴承总体磨损量增加，且在重力和微重力环境中轴承的磨损分布区间相同。但是，在重力环境中轴承在0°～180°区间即轴承上部的磨损较轻微，在190°～360°区间即轴承下部的磨损严重。在轴承圆周位置为270°附近即重力方向时轴承的磨损程度最严重，其磨损深度为微重力环境中的1.42倍左右；在轴承圆周位置为90°附近，即重力反方向时，其磨损程度最小，且比无重力时在此位置的磨损程度要小很多，其磨损深度只有微重力环境中的0.59倍左右。在0.5g重力环境中，由于所受重力作用减弱，轴承圆周位置为270°附近即重力方向时的磨损深度为微重力环境中的1.2倍左右，在轴承圆周位置为90°附近，即重力反方向时其磨损深度为无重力环境下的0.79倍左右，其不同区间的磨损程度介于重力环境和微重力环境之间。轴承的磨损趋势与其对应的轨迹图8(b)所预测的结果吻合。

当机械臂的旋转速度为10π rad/s时，从图9(c)可以看出，由于转速的继续增加，使得轴承总体磨损量更大。虽然在重力环境中轴承的磨损沿着轴承内壁的不同区间呈一定的正弦分布，但是其影响相对于较低速度时要小很多。在轴承圆周位置为270°附近即重力方向时，轴承的磨损深度为微重力环境中的1.1倍左右；在轴承圆周位置为90°附近，即重力反方向时，其磨损程度为微重力环境中的0.87倍左右。在0.5g重力环境中，由于所受重力作用减弱，其不同区间的磨损情况相对于微重力环境的中的更加接近。结合其对应的轴心轨迹图8(c)可知，在此速度下，重力对轴承的磨损的影响相对较小。

图10(a)，图10(b)，图10(c)对比了不同转速下重力对最大磨损间隙随机械臂旋转周期的变化过程的影响。由图10可知，在磨损初期，磨损率逐渐减小，这是由于磨损初期接触面积增大导致的，然后磨损逐渐进入稳定磨损阶段，磨损间隙的增长率基本保持不变，其磨损变化过程与文献[19]中的数值模拟结果相符。如图10(a)所示，当转速为2π rad/s时，即速度相对较低时，在微重力环境中磨损间隙增长缓慢，且间隙值相对较小。在重力环境中，由于重力远大于离心力，使得轴承的磨损集中，磨损间隙快速增加，其磨损间隙值的增长率比微重力环境中大很多倍，将严重影响机械臂的性能和精度，此时重力对磨损间隙的影响很大。在0.5g重力环境中，磨损间隙增长率相比于重力环境大幅减小，主要由于轴承的磨损分布区间增大和重力作用减小共同造成的；如10(b)所示，当转速为6π rad/s时，此时在不同重力环境中，轴承的最大磨损间隙的值都较大且增加较快。虽然重力环境中的磨损间隙值比微重力环境中大，且在稳定磨损阶段间，磨损间隙增长率要快，但是其差距比转速为2π rad/s时要小很多，且当重力作用减弱时，磨损间隙增长率也相应降低。如图10(c)所示，当转速为10π rad/s时，虽然在重力环境中磨损间隙比微重力环境中稍大，但在稳定磨损阶段，其磨损增长率已经非常接近。当重力作用减弱时，其磨损增长率与微重力环境下更加接近。可见，在此速度下重力对磨损间隙的影响更小。

4 结 论

通过建立磨损与动力学耦合分析模型，分析并计算了不同重力环境下间隙关节的磨损情况。结果表明，在低速时，重力对间隙关节的磨损分布和磨损程度都有很大影响，由于离心力远小于重力，轴与轴承的接触和磨损主要集中在轴承下部有限的固定区间，使得磨损间隙急剧增加，将严重影响机构的性能和精度。当重力作用减弱时，对应的磨损分布区间增加，轴承磨损深度和磨损间隙的增长率都大幅减小；随着转速的增加，离心力大于重力后，轴与轴承的接触轨迹将沿着轴承圆周分布，重力只对轴承不同区间的磨损程度有影响；当转速继续增加，重力相对比离心力将越来越小，轴承不同区间的磨损程度和磨损间隙的增长率将逐渐与微重力状态下接近。并且所建立的磨损与动力学耦合计算模型将磨损过程离散化，实现了对复杂的动态、非线性磨损过程的模拟。该方法不仅保证了计算的时效性，还能真实地反映含间隙铰接副接触表面的动态磨损状况，对工程机械设计和动力学分析及磨损预测具有重要理论意义和应用价值。

[1] 白争锋, 赵阳, 田浩. 含铰间间隙太阳帆板展开动力学仿真[J]. 哈尔滨工业大学学报, 2009, 41(3): 11-14. [Bai Zheng-feng, Zhao Yang, Tian Hao. Dynamics simulation of deployment for solar panels with hinge clearance [J]. Journal of Harbin Institute of Technology, 2009, 41(3): 11-14.]

[2] 游斌弟, 潘冬, 赵阳. 关节铰间隙对漂浮基星载天线扰动研究[J]. 宇航学报, 2010, 31(10): 2251-2258. [You Bin-di, Pan Dong, Zhao Yang. Research on disturbance of joints with clearance on free-floating satellite antenna [J]. Journal of Astronautics, 2010, 31(10): 2251-2258.]

[3] Erkaya S. Investigation of joint clearance effects on welding robot manipulators [J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(4): 449-457.

[4] 马兴瑞. 航天器动力学: 若干问题进展及应用[M]. 北京: 科学出版社, 2001.

[5] Flores P. Modeling and simulation of wear in revolute clearance joints in multibody systems [J]. Mechanism and Machine Theory, 2009, 44(6): 1211-1222.

[6] Mukras S, Kim N H, Sawyer W G, et al. Numerical integration schemes and parallel computation for wear prediction using finite element method [J]. Wear, 2009, 266 (7-8): 822-831.

[7] Mukras S, Mauntler N A, Kim N H, et al. Modeling a slider-crank mechanism with joint wear [J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2009, 2(1): 600-612.

[8] Su Y, Chen W, Tong Y, et al. Wear prediction of clearance joint by integrating multi-body kinematics with finite-element method [J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2010, 224(8): 815-823.

[9] 宿月文, 陈渭, 朱爱斌,等. 铰接副磨损与系统动力学行为耦合的数值分析[J]. 摩擦学学报, 2009, 29(1): 50-54. [Su Yue-wen, Chen Wei, Zhu Ai-bin, et al. Numerical analysis of wear coupling with dynamics behavior of machine [J]. Tribology, 2009, 29(1): 50-54.]

[10] 朱爱斌, 何胜利, 邹超,等. 考虑接触刚度的含间隙铰接副动态磨损分析[J]. 西安交通大学学报, 2016, 50(5): 12-18. [Zhu Ai-bin, He Sheng-li, Zou Chao, et al. Dynamic wear analysis of clearance joint considering contact stiffness [J]. Journal of Xi’an Jiaotong University, 2016, 50(5): 12-18.]

[11] Zhao Y, Bai Z F. Dynamics analysis of space robot manipulator with joint clearance [J]. Acta Astronautica, 2011, 68(7-8): 1147-1155.

[12] Erkaya S. Modeling and simulation of joint clearance effects on mechanisms having rigid and flexible links [J]. Journal of Mechanical Science and Technology, 2014, 28(8): 2979-2986.

[13] Bai Z F, Zhao Y. A Hybrid contact force model of revolute joint with clearance for planar mechanical systems [J]. International Journal of Non-Linear Mechanics, 2013, 48(48): 15-36.

[14] Cosmi F, Hoglievina M, Fancellu G, et al. A Finite element method comparison of wear in two metal-on-metal total hip prostheses [J]. Proceedings of the Institution of Mechanical Engineers Part H Journal of Engineering in Medicine, 2006, 220(8): 871-879.

[15] 宋宝玉, 古乐, 邢恩辉. 真空条件下GCr15钢摩擦磨损性能研究[J]. 哈尔滨工业大学学报, 2004, 36(2): 238-241. [Song Bao-yu, Gu Le, Xing En-hui. Friction and wear properties of GCr15 steel under vacuum condition [J]. Journal of Harbin Institute of Technology, 2004, 36(2): 238-241.]

[16] Flores P. Modeling and simulation of wear in revolute clearance joints in multibody systems [J]. Mechanism and Machine Theory, 2009, 44(6): 1211-1222.

[17] Bai Z F, Zhang H B, Sun Y. Wear prediction for dry revolute joint with clearance in multibody system by integrating dynamics model and wear model [J]. Latin American Journal of Solids and Structures, 2014, 11(14): 2624-2647.

[18] Öqvist M. Numerical simulations of mild wear using updated geometry with different step size approaches [J]. Wear, 2001, 249(1-2): 6-11.

[19] Mukras S M. Analysis and design of planar multibody systems with revolute joint wear[D]. Gainesville: University of Florida, 2009.