固体微推力器阵列的推力估计与分配补偿方法
2018-05-07刘旭辉
杨 博,赵 旭,苗 峻,刘旭辉,龙 军
(1.北京航空航天大学宇航学院,北京 100191;2.北京控制工程研究所,北京 100190)
0 引 言
微推力器阵列利用微机电技术在同一块芯片上集成大量独立可寻址的微推力器,具有高集成度、体积小、质量轻、结构简单、无可移动部件、没有液体泄漏、制作简单等优点。早在20世纪90年代,TRW公司就设计了这种推力器;此后,法国、韩国和日本的相关科研机构也设计了自己的微推力器阵列;清华大学、国防科技大学等少数高校也制备了原理样机进行测试[1]。传统推进系统体积质量比较大,而微纳卫星的体积质量小、功率电压低,所以传统推进系统并不适合应用在微纳卫星上,而微推力器阵列克服了传统推力器体积大质量大的劣势,因此受到了广泛地关注和研究[2-3]。
采用微推力器阵列进行控制的微纳卫星,是一个标准的过驱动系统。过驱动系统中存在的硬件冗余,使得针对系统的进一步优化成为可能,为了充分利用这一特点提升航天器性能,引入了推力分配环节来对上层控制律给出的需求推力进行进一步优化,即引入推力分配将控制律计算得到的名义控制力分配给冗余配置的推力器[4]。针对推力分配问题,在许多文献中已经给出一些具体的方法,如查表法[5]、动态分配法[6]和负载均衡法[7-8]。然而在实际应用中,仅控制律稳定并不能保证引入了推力分配环节后系统依然稳定,以上推力分配的文献中均没有针对这一问题进行分析。虽然文献[9]针对这一问题提出了一种类PD反馈的方法来保障引入推力分配后的闭环系统仍然稳定,但该方法在推力分配环节采用了能够获得解析解的伪逆分配法,对于不采用伪逆法进行推力分配的系统,其稳定性仍然少有文献进行分析。
在实际应用中,微推力器的推力测量也是一个难点,其推重比非常小,产生的推力也极小,对测量环境及测量方法也提出了很高的要求[3]。我国的微小推力器还处于发展阶段,实现高精度的测量所需技术要求和成本都很高。因此考虑到受燃料消耗、推力器部件老化以及地面测试不准确等原因的影响,实际使用时推力器产生的推力会偏离标称推力,为了保证控制系统的性能,在推力分配中也应该考虑推力偏差的影响。在处理推力偏差问题上,Castaldi等[10]利用微分几何方法来处理非线性系统中的执行器故障估计问题,在飞行器容错控制中获得了较好的效果。Alessro[11]首次在控制分配模块进行推力估计,但由于配置于传统的推力分配系统,并没能证明系统的稳定性。Ye[12]利用偏差导数信息以及自适应观测器的方法重构执行器乘性效率因子,但该方法需要知道推力偏差的变化率,实际应用价值受限。
针对以上问题,本文引入效率因子来描述推力偏差,并利用二次规划进行效率因子估计,讨论了估计算法的收敛性。在此基础上,针对微推力器一次性点火的特性,结合效率因子估计值,建立混合整数规划模型进行推力分配,使得系统能够估计推力偏差并对其进行实时补偿,最后研究了引入推力分配后系统稳定性问题。
1 推力分配基本问题描述
对于过驱动系统,引入推力分配后控制系统的基本结构如图1所示。
推力分配的目的,即考虑执行机构冗余与物理约束,将控制律给出的名义控制力以某种优化指标分配给具体的执行机构,从而实现系统性能的进一步提升。
考虑线性离散系统
x(t+1)=Ax(t)+Bv(t)
(1)
式中:x(t)∈Rn为t时刻的状态向量,A∈Rn×n为系统矩阵,B∈Rn×m为输入矩阵,v(t)∈Rm为t时刻的虚拟控制输入。
对过驱动系统进行推力分配,有
v(t)=Cu(t)
(2)
式中:C∈Rm×k为分配矩阵,u(t)∈Rk为实际控制力,m 在分配中考虑推力偏差,引入效率因子,则在推力偏差下式(2)可写为 v(t)=CΨ(t)u(t) (3) 式中:Ψ(t)=diag(ψ1(t),…,ψk(t)),ψi(t)表示第i个控制力的实际效率,ψi(t)=1表示该轴实际控制力与标称控制力相同。 推力分配问题的关键在于如何求解不定方程式(3)以及如何确定效率因子矩阵Ψ(t)。 由于在实际使用中一般更关心微推力器阵列上推力器的消耗个数,将式(3)改写为 v(t)=C′G(t)z(t) (4) 式中:G(t)=diag(g1(t),…,gk(t)),gi(t)表示第i个推力器的实际效率,gi(t)=1表示该推力器实际推力与标称推力相同。z(t)∈Nk,zi表示第i个推力器阵列上消耗微推力器的个数,C′∈Rm×k为分配矩阵。 由于推力分配过程总是在一个时刻进行,为了简便,推力分配建模过程中不再引入t。 推力分配优化目标选择燃料最优,即选取目标函数为 (5) 将目标函数与约束结合,则可以写成如下优化问题 s.t.C′Gz=v,z∈Nk (6) 由于执行器不可能完美无误执行上层控制力,引入分配误差弱化模型约束,取误差变量为 C′Gz-v=e=e+-e- (7) 式中:e为分配误差,e+,e-中元素均非负。 则可以得到存在分配误差的优化模型 minJ=∑ki=1zis.t.e+-e-=C′Gz-vz∈Nk,e+≤emax,e-≤emax{ (8) 式中:emax为容许最大推力分配误差。 针对该模型的求解问题是一个混合整数规划问题,为便于求解将其转化为标准优化模型的形式 minlTys.t.Dy=-vy≥0,z∈Nk,e+≤emax,e-≤emax{ (9) 这样就得到了一个标准的混合整数规划模型,利用现已成熟的数学优化算法(如分支定界法,内点法等)就可以进行优化求解,进行在容许分配误差下的最省燃料分配。 注2. 无论取何种式(9)的变形体,约束中需有e+≤emax,e-≤emax,即分配误差有界,该条件是稳定性分析中的重要条件。为了保证式(9)有解,同时燃料尽可能少消耗,在已知G的情况下一般选择emax为微推力阵列所能产生的单位推力。 注3. 假设一个推力器阵列上的微推力器推力均相等,阵列平贴于立方星表面,由于每个微推力器产生推力效应相同,在不考虑姿态的情况下,可建模为式(9)的形式,只关心每个阵列上点火几个微推力器。 注4. 在考虑小卫星姿态的情况下,有时候需要针对推力器阵列上的每一个推力器进行分配建模,即将式(9)的混合整数规划模型变形为0-1规划模型(混合整数规划的特例),1代表该微推力器点火,即有 minlTy′s.t.D′y′=-v,y′≥0z′∈Nk,0≤zi≤1,i=1,2,…,ke+≤emax,e-≤emaxìîíïïïï (10) 由于微推力器阵列上的微推力器一次性使用的特性,每一次分配结束后需要将C″矩阵中对应该微推力器的列置0或剔除,防止下一次分配中再使用该微推力器。 从推力分配模型中可以看出,在已知效率因子的情况下,通过推力分配能够在不修改上层控制律的情况下很好地补偿实际推力器偏差,然而实际中,效率因子真值很难获得,只能通过对系统状态的测量来对效率因子进行一个估计,而估计的优劣程度则代表了最后推力分配中补偿的优劣。 考虑实际工艺,在制作一片微推力器阵列时,其每一个微推力器具有相同的推力大小,即每一片微推力器阵列上的推力器具有相同的效率因子,那么在估计效率因子时,可用该片已经使用的推力器来估计其他推力器的推力。 考虑到二次规划问题在优化领域中研究得比较深入,只需要建立其数学估计模型,有非常成熟的优化算法可以对其进行求解。这里采用一种二次规划进行效率因子估计的方法。该估计算法通过对过去p个采样点系统状态信息的处理,得到在这p个点中效率因子增量的一个优化估计值,根据效率因子增量估计值可以计算得到效率因子的估计值。 将推力分配式(4)代入模型(1),可得 x(t+1)=Ax(t)+BuG(t)z(t) (11) 式中:Bu=BC′。 为了能够进行效率矩阵估计,首先定义效率矩阵增量如下 Φ=G(t)-G(t-1) (12) 式中:Φ=diag(φ1,…,φk),φi=gi(t)-gi(t-1)。 第一步:求解以下二次规划问题 min ∑pi=1^sTi^sis.t. x(t)-Ax(t-1)-Bu(^G(t-1)+^Φ)· z(t-1)=^s1x(t-1)-Ax(t-2)-Bu(^G(t-1)+^Φ)· z(t-2)=^s2︙x(t-p+1)-Ax(t-p)-Bu(^G(t-1)+^Φ)· z(t-p)=^spìîíïïïïïïïïïïïï (13) (14) (15) (16) (17) 为了讨论二次规划算法对于慢时变效率因子的估计能力,设t′为推力发生偏差的时刻,同时假设在发生偏差后一段时间内,效率因子保持不变。 定义估计误差如下 (18) (19) 证.实际上可以假设t′时刻后真实效率因子矩阵为G′,那么在t>t′时 x(t+1)=Ax(t)+BuG′z(t) (20) 在最小拟合误差均为0的情况下,可以认为存在多个增量矩阵Φ满足式(14)中的约束条件。即 (21) 式中:Q代表优化问题式(14)可行解的集合, 式(13)有解,则可行解约束方程 (22) 从定理1可以看出,要求对所有推力器的效率因子都能准确估计,需要在过去p个采样点中,所有推力器都有独立的推力输出,即对于p个推力器阵列,至少需要p个采样点信息才能保证算法收敛。 根据推力分配模型以及推力估计算法,可以得到推力估计与分配补偿方法的流程图(见图2)。 一般研究推力分配的文献中很少讨论引入分配之后系统的稳定性问题,但实际上,由于引入了推力分配,同时采用了二次规划的方法对效率矩阵进行估计,那么控制系统的稳定性必然会受分配误差的影响,而分配误差又主要受到推力估计误差的影响。本文将对该部分影响进行一个理论分析。 假设v′为推力分配给出的实际控制力,代入式(1),可得 x(t+1)=Ax(t)+Bv′(t) (23) 考虑状态反馈控制 v(t)=-Kx(t) (24) 则有 x(t+1)=Ax(t)+Bv′(t)+B(-Kx(t))- B(-Kx(t))=(A-BK)x(t)+ B(v′(t)-(-Kx(t)))=(A- BK)x(t)+B(v′(t)-v(t)) (25) 实际上 v′(t)-v(t)=C′Gz-v(t)=e (26) 所以 x(t+1)=(A-BK)x(t)+Be (27) 从式(9)的约束条件中可以得到 |e|≤emax (28) 式中:|*|代表对每一个元素取绝对值。 式(27)所描述的运动稳定,首先需要(A-BK)的特征值均在单位圆内,同时系统存在一个有界外扰动,针对这样的系统,文献[14]证明是一个有界稳定系统,其最终收敛于集合C。 |V-1B|emax+|V|ζ} (29) 以上推导基于式(9)存在解,为了保证式(9)总是有解,取emax中的最小分量为μ,需保证 (30) 注6.由于该收敛界的计算基于最大推力分配误差,然而实际中并不会每次分配都以分配误差最大的情况出现,所以该收敛界的计算具有一定的保守性。 考虑编队近距离和主星圆轨道的情况,从星在Hill坐标系下的相对运动方程可以简化成Clohessy-Wiltshire方程模型[15]: (31) 式中:ωt为主星轨道平均角速度,f为控制加速度。 则有 (32) 式中: 取采样周期T=0.1 s,对模型离散化有 x(t+1)=Ax(t)+Bv(t) (33) 与文献[1]类似,取编队构形为等边三角形,三颗从星分别位于三角形的三个顶点,一颗主星位于三角形的中心,构形尺度为1.5 m,四颗卫星均为立方星,尺寸为10 cm×10 cm×10 cm,质量为1 kg。主星轨道选择低轨太阳同步轨道,各星初始时标准轨道参数如表1所示。 由于三颗从星控制效应类似,为了节省篇幅,本文主要以从星1的结果来说明。取从星1的初始偏差e1=[2, -2.5, 2, 0.5, -1.2, 1]T,即从星1与其标准位置/速度的偏差。考虑推力器阵列单位推力为0.01 N,产生的推力为0.01 N的整数倍,则分配矩阵有 (34) 取各推力器效率因子初值为1,推力器的真实效率因子为g=[1.2 1.3 0.9 0.7 0.8 1.1]T,p=6 ,假设同一个阵列上的微推力器具有相同的效率,且推力偏差初始时刻即存在,采用本文所提推力估计方法进行在线推力估计,6个推力器的效率估计如图3~4所示。 表1 编队卫星初始标准轨道要素Table 1 Initial orbital elements of formation satellites 从图3~4可以看出,在初始时便出现效率因子偏差的情况下,利用二次规划算法可以很好地估计常值效率因子,6个推力器的效率因子估计值基本都收敛到真值,即获得了推力器的真实推力。 同时考察从星1的位置误差变化过程,得到图5~7所示的位置偏差曲线。其中,理想控制指未出现推力偏差的情况;实际控制指出现推力偏差但未采用本文方法进行估计补偿;本文方法指采用推力估计与分配方法进行推力偏差实时估计与补偿。 从图5~7可以得出以下结论: 1)利用推力估计与分配算法,能够在推力器出现推力偏差的情况下,让系统的状态响应接近无推力偏差的情况。 2)不采用该推力估计与分配算法,由于推力偏差的存在,使得系统动态响应过程与标准响应有所偏离,如图5中稳定后曲线完全偏离标准响应,而图6、图7则出现了高于标准控制曲线的超调。 3)若K矩阵根据实际要求进行极点配置或者采用最优理论设计,那么不采用该分配算法,则可能在实际使用中出现推力偏差时丧失最优性或者动态性能,从而出现非预期的效果。 4)该方法使得推力器在出现推力偏差后系统的动态、稳态特性仍能保持近似不变,提升微推力器的工作能力,保障实际控制性能,减轻地面测试中对推力测量的要求,降低测试成本,为微推力器的在轨工程应用打下基础。 针对实际使用中微推力器推力输出无法准确测量的问题,本文采用一种二次规划方法对实际推力进行估计,并利用混合整数规划算法进行微推力器的推力分配,实现推力偏差的实时估计与补偿。仿真结果表明,该方法能够很好地估计常值效率因子,同时配合推力分配策略,可以保证推力器在出现推力偏差时系统的状态响应仍然与未出现推力偏差时的标准状态响应近似相同,保障了系统在出现推力偏差时的控制性能,并证明了采用该分配算法的系统有界稳定。 [1] 范林东,杨博,苗峻,等. 基于SiC MEMS阵列的高精度微纳卫星编队保持[J]. 中国空间科学技术, 2016, 36(2):37-45. [Fan Lin-dong,Yang Bo,Miao Jun,et al. High precision micro-nano satellite formation keeping based on SiC MEMS micro thrust array[J]. Chinese Space Science and Technology, 2016, 36(2):37-45.] [2] 杨灵芝, 魏延明, 刘旭辉. MEMS固体微推力器阵列发展研究[J]. 空间控制技术与应用, 2016, 42(1):13-19. [Yang Ling-zhi, Wei Yan-ming, Liu Xu-hui. Development of MEMS solid propellant micro-thruster array[J]. Chinese Space Science and Technology, 2016, 42(1):13-19.] [3] 刘旭辉,方蜀州,马红鹏,等. 基于固体微推力器阵列的卫星控制一体化算法[J]. 固体火箭技术, 2012, 35(1):17-23. [Liu Xu-hui,Fang Shu-zhou,Ma Hong-peng,et al. Integrated control algorithm based on solid propellant micro-thruster array[J]. Journal of Solid Rocket Technology, 2012, 35(1):17-23.] [4] Johansen T A, Fossen T I. Control allocation-a survey[J]. Automatica, 2013, 49(5):1087-1103. [5] 王敏, 解永春. 考虑推力器推力上界及故障情况的航天器实时指令分配最优查表法[J]. 宇航学报, 2010, 31(6):1540-1546. [Wang Min,Xie Yong-chun. Spacecraft thrusters real-time command allocation algorithm in consideration of thrust upper bounds and thruster failure[J]. Journal of Astronautics, 2010, 31(6):1540-1546.] [6] 唐生勇,张世杰,陈闽,等. 交会对接航天器推力器分配算法研究[J].宇航学报, 2008, 29(4):1120-1125. [Tang Sheng-yong,Zhang Shi-jie,Chen Min,et al. Research on a thrust allocation algorithm of spacecraft in RVD[J]. Journal of Astronautics, 2008, 29(4):1120-1125.] [7] 张世杰,段晨阳,赵亚飞. 考虑负载均衡的过驱动航天器推力器分配方法[J]. 宇航学报, 2015, 36(7):826-832. [Zhang Shi-jie, Duan Chen-yang, Zhao Ya-fei. Thruster allocation for over-actuated spacecraft with load balancing[J]. Journal of Astronautics, 2015, 36(7):826-832.] [8] Bodson M, Frost S A. Load balancing in control allocation[J]. Journal of Guidance Control & Dynamics, 2012, 34(2):380-387. [9] Hu Q, Li B, Zhang Y. Nonlinear proportional- derivative control incorporating closed-loop control allocation for spacecraft[J]. Journal of Guidance Control & Dynamics, 2014, 37(3):799-812. [10] Castaldi P, Mimmo N, Simani S. Differential geometry based active fault tolerant control for aircraft [J]. Control Engineering Practice, 2014, 32:227-235. [11] Alessro C, Emanuele G. Fault‐tolerant adaptive control allocation schemes for over-actuated systems[J]. International Journal of Robust & Nonlinear Control, 2010, 20(17):1958-1980. [12] Ye D, Park J H, Fan Q. Adaptive robust actuator fault compensation for linear systems using a novel fault estimation mechanism[J]. International Journal of Robust & Nonlinear Control, 2016, 26(8):1597-1614. [13] Seron M M, De D, Jose A. Robust actuator fault compensation accounting for uncertainty in the fault estimation[J]. International Journal of Adaptive Control & Signal Processing, 2014, 28(12):1440-1453. [14] Kofman E, Haimovich H, Seron M M. A systematic method to obtain ultimate bounds for perturbed systems[J]. International Journal of Control, 2007, 80(2):167-178. [15] 张世杰, 段广仁. 分布式卫星编队飞行队形保持协同控制[J]. 宇航学报, 2011, 32(10):2140-2145. [Zhang Shi-jie, Duan Guang-ren. Cooperative control for distributed satellites formation keeping[J]. Journal of Astronautics,2011, 32(10):2140-2145.]2 推力分配模型
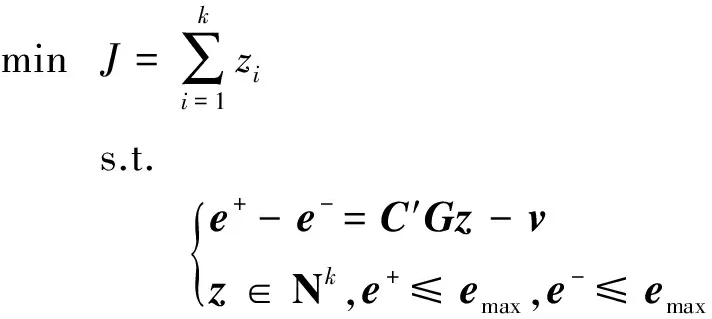
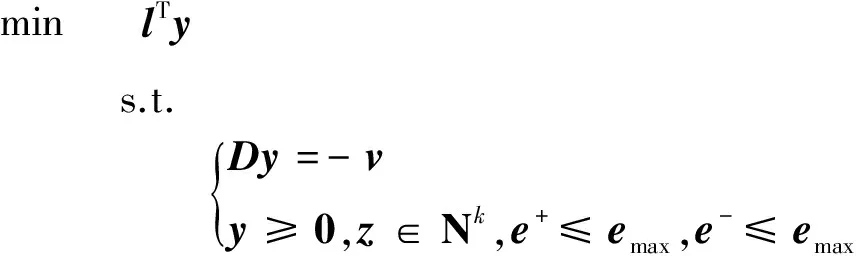
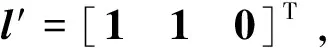

3 效率因子估计算法
3.1 基于二次规划的估计算法
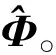



3.2 算法性能分析

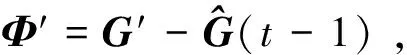
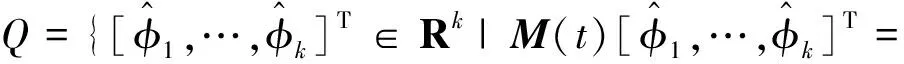


4 系统稳定性分析
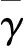
5 仿真校验
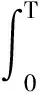


6 结 论
