基于NVPA算法的社交网络影响力最大化算法*
2018-05-05徐浩,潘理
徐 浩,潘 理
(1.上海交通大学 电子信息与电气工程学院,上海 200240;2.上海市信息安全综合管理技术研究重点实验室,上海 200240)
0 引 言
随着在线社交网络分析在推荐系统、市场营销、信息检索等依据影响力对用户行为进行预测的领域的广泛应用,影响力分析问题在学术界和工业界引起了越来越多重视。基于社交网络的市场营销,如何准确找到最具影响力的个体集合、获取最大的影响范围,是极其关键的问题。对此,文献[1]给出了准确化定义,将影响力最大化问题转化为如何选择K个初始节点,通过激活这K个初始节点,在给定信息传播模型下,使网络中最终被激活的用户节点数最多。已有的相关研究主要从个体的角度分析问题[2-4],Kempe等人[2]首先使用贪婪爬山算法进行影响力分析,证明了这一问题是NP难问题,用贪婪算法求解可以达到(1-1/e)的精度。但是,贪婪算法的时间复杂度太高。后来研究人员主要解决的问题是提高算法的运行效率[5,6],但是这些算法都是基于网络全局进行算法模型设计。当面对大规模社交网络时,过高的时间复杂度依旧是一个棘手的难题。因此,本文基于NVPA[7]社区划分算法,提出了一种从局部角度解决影响力最大化问题的算法NVPA-IM。在传统的社区划分算法中,相似度衡量指标一般都是节点的一跳邻居节点数的重合度,而忽略了多跳邻居节点集对相似度的影响。相对于传统算法,NVPA算法在计算节点之间的相似度时,考虑了节点的多跳邻居节点对相似度的贡献,显著提高了社区划分的精度。同时,传统的社区划分算法一般将模块度指标[8]作为衡量社区划分好坏的重要指标,以模块度最优作为社区划分过程迭代终止的判断条件。所以,最终网络中社区的个数并不能确定。相对于传统社区划分算法,NVPA算法在保证模块度指标优异的情况下,可以将网络指定划分成K个社区。经实验验证,该算法能够精确挖掘网络中的社区结构。
1 NVPA-IM算法
在社交网络研究中,一般将社交网络抽象成一张有向(或无向)图G=(V,E)。其中,用户抽象成节点,V={v1,v2,…,vn}为节点集合。用户之间的关系抽象成边,E={(vi,vj)|vi,vj∈V}为边的集合。
定义1 影响力最大化。给定一个社交网络G=(V,E)和一个正整数K,要求从社交网络中寻找K个初始活跃节点集合S(|S|=K,S⊆V),S在社交网络中按照某种信息传播规律传播影响,要求最终活跃的节点数目最多。用影响力函数σ(·)表示社交网络中最终活跃节点的数目。影响力最大化问题即要求寻找合适的集合S使得σ(·)最大化,一般将集合S称为种子集,形式化描述如下:

1.1 NVPA算法
NVPA算法是一种基于社交网络结构而进行社区划分的算法。如上介绍,为了更精确地挖掘网络的社区结构,在计算节点之间相似度时,NVPA算法考虑了与节点距离为d(d>1)的邻居节点对结果的影响。该算法定义节点的m跳邻居节点集如下:
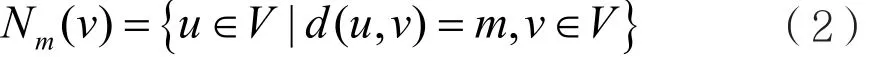
式中d(u,v)是节点u到节点v的距离。同时,该算法定义邻域向量Zi用于保存节点i的拓扑结构信息。Zi是归一化向量,能够有效表示节点在空间中所处的位置。在一个具有n个节点的网络图中,节点vi的邻域向量定义为:
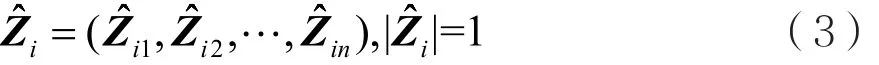
在n维欧式空间中,Z^i是一个单位向量,反映了节点和其邻居节点之间的关系。基于以上两个定义,NVPA算法设计了一个邻域向量传播规则:
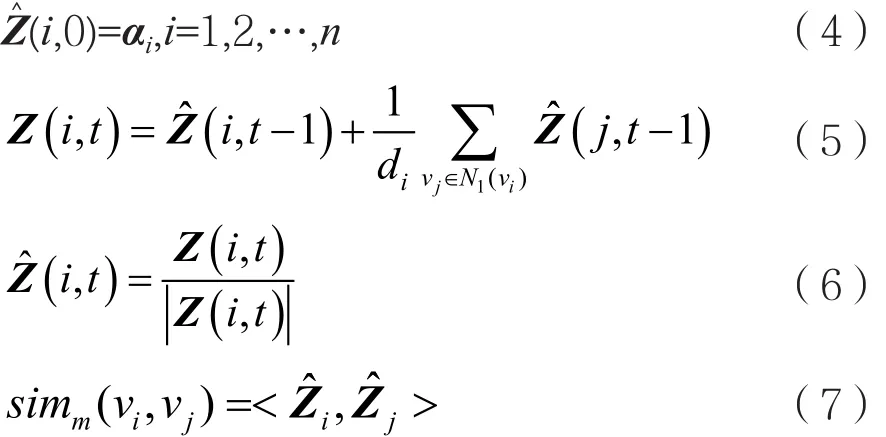
式(4)对节点的邻域向量进行初始化,{α1,α2,…,αn}是欧式空间 Rn的正交基;式(5)中 di表示节点的度。依据式(5)、式(6),循环更新节点的邻域向量值m次,则每个节点的邻域向量Zi都包含了节点的m跳及m跳以内的邻居节点的网络拓扑结构信息。基于节点的邻域向量计算相邻节点的cosine相似度即式(7),将相似度最大的两个节点vi、vj组合成一个社区,用节点vi表示该新社区,同时将节点vj从网络中删除。最后,按照一定的降维规则将维度αj删除。循环以上过程,直至网络中只包含K个节点时,社区划分结束,这K个节点即是获取的K个社区。
1.2 种子节点选取
利用NVPA算法划分后的网络包含K个节点,每个节点代表一个社区。从每个社区中挖掘出一个影响力最大的种子节点,即组成种子集S。通常,启发式算法在选取种子节点时效率较高,如传统的度中心算法。该算法认为,社区中度最大的节点即一跳邻居节点数最多的节点,在传播过程中具有重要作用。由NVPA算法可知,节点在网络结构中的重要性也受节点的m跳及m跳以内邻居节点数的影响。所以,本文设计了基于式(8)的种子节点选取算法NVPA-IM:

该算法基于NVPA算法的性质,对度中心算法进行扩展。在NVPA社区划分算法中,计算相邻节点之间的相似度时考虑到了距节点距离小于等于m的所有邻居节点对节点之间相似度的贡献,即相对于传统的相似度算法,NVPA算法在计算相邻节点相似度时不仅仅只考虑一阶邻居节点数目。所以在选取社区中重要的节点时,本文将度中心算法的衡量指标一跳邻居节点数扩展到m跳及m跳以内的邻居节点数,m的取值由社区划分阶段邻域向量的传播次数决定。在式(8)中,Ni(v)是节点v的i跳邻居节点集合包含的节点数。Γm(v)值越大,说明以节点v为中心,到节点v距离为m及m以内的节点集覆盖的范围越广,节点v在影响力传播方面的作用越大。在社区划分阶段,一般情况下设置m为2~4的整数。在本文实验阶段,设置m的值为3。综上所述,NVPA-IM算法的伪代码如下:
输入:网络G=V∈E;邻域向量传播次数m;种子节点数K
输出:包含K个节点的种子集S

//第一部分:社区划分
2 for each viin V, do:
3 根据式(4)初始化节点vi的邻域向量
4 for t=1 to m,
5 根据式(5)和式(6)更新网络中每一个节点的邻域向量
6 for each eijin E, do:

8 for l=1 to n-K
9 选择相似度最大的两个节点vi,vj,将它们组合成一个新社区,用vi表示该社区
//空间降维

13 删除维度αj并且归一化更新后的邻域向量
//第二部分:种子节点选取
14 for each Ci
15 for each v in Ci

17 在社区Ci中选择Γm(v)值最大的节点v
18 S=S∪v
19 return S
可见,NVPA-IM算法首先利用NVPA算法对社交网络进行社区划分(lines1~lines13)。该阶段中,网络中每一个节点都代表一个社区。因此,line9中是将社区vj组合到社区vi中,且line10中的ni、nj分别表示社区vi、vj中用户的个数。然后,该算法从每个社区中进行种子节点选取(lines14~lines18),用社区C1,C2,…,Ck表示第一部分社区划分的结果v1,v2,…,vk,并依据Γm(v)指标挖掘种子节点集。
2 实验与结果分析
本文实验使用Mcauley[9]于2012年从Facebook上获取的数据集和文献[10]中提到的LRF基准网络数据集。LRF数据集是人工数据集。在生成该数据集的过程中,同时考虑了社区内部的紧密连接特征和现实世界复杂网络的真实特征。Facebook数据集包含4 039个节点和88 234条边;LRF人工数据集包含1 000个节点和9 935条边。本文实验的实验环境是Intel Corei7-6700 3.4G处理器,16 GB内存。
为了便于对比分析,在实验阶段主要用影响收益来评估算法的性能。影响收益是指在社交网络中选取K个初始节点并激活,在影响传播结束后,网络中被激活的节点数w与网络中节点总数n的比值w/n。该值的取值范围是0~1。算法的影响收益越大,说明该算法的种子节点集选取的越准确。通过激活该种子节点集合获取的信息,传播范围越广。
本文实验内容主要包括两部分:(1)从影响收益角度验证NVPA社区划分算法的性能;(2)通过与已有的种子挖掘算法对比,验证NVPA-IM算法的精度与效率。算法精度主要用影响收益衡量,而算法效率主要用实验运行时间衡量。
首先,为了评估NVPA社区划分算法在解决影响力最大化问题时的性能,本文将其和目前已有的几种典型的社区划分算法进行对比,即基于模块度最大化的贪心算法FN[11]、基于图的半监督学习算法标签传播算法LPA[12]和基于相似度的聚合算法H-Clustering[13]。在实验结果分析阶段,本文先利用以上4种社区划分算法将网络进行社区划分,然后依据社区规模大小选择前K个社区,随机从每个社区中选择一个节点组成种子节点集,最后在独立级联传播模型(IC)上对比分析种子节点集的影响收益。在该阶段,种子节点数目K的取值范围是1~15。同时,下文分别用NVPA-R、FN-R、H-Clustering-R、LPA-R表示以上4种种子节点选取算法。
在IC模型中,本文设置每条边的传播概率为0.05。在LRF数据集上,4种社区划分算法的影响收益如图1所示。

图1 不同社区划分算法在LRF数据集上的影响收益对比
如图1所示,当种子节点数目K属于1~15时,FN-R、LPA-R、H-Clustering-R这3种算法的影响收益近似,而NVPA-R算法的影响收益要明显优于其余3种算法。在Facebook数据集上,4种社区划分算法的影响收益如图2所示。
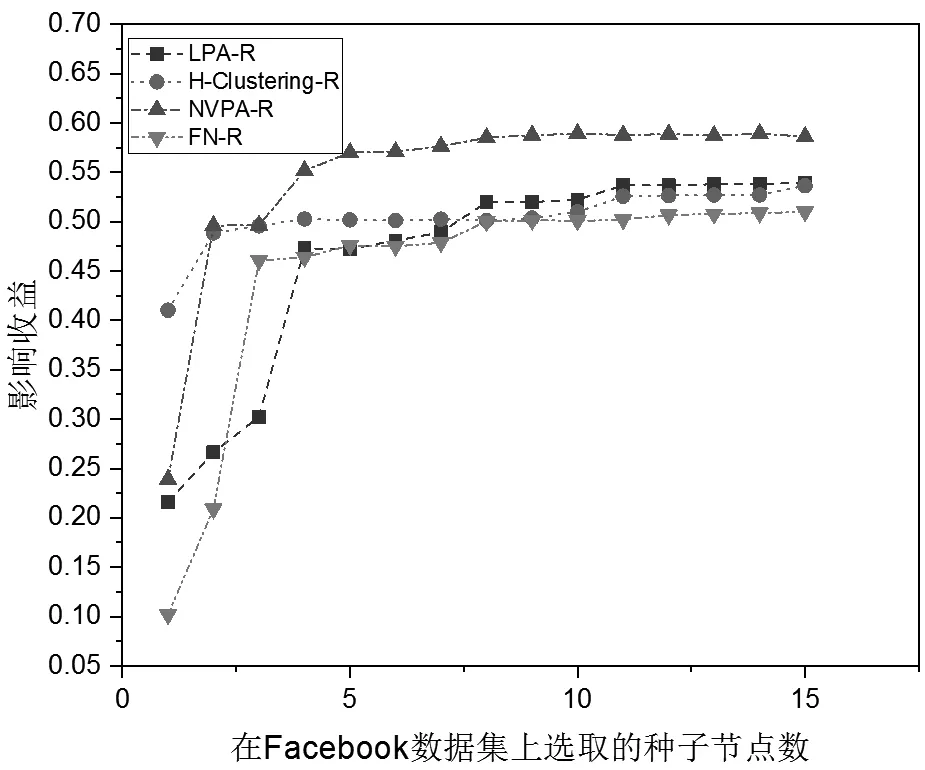
图2 不同社区划分算法在Facebook数据集上的影响收益对比
如图2所示,随着K值的增加,FN-R、LPA-R、H-Clustering-R及NVPA-R这4种算法的影响收益都趋于稳定,且前3种算法的影响收益要明显小于NVPA-IM算法。由以上实验结果可知,对于从社区角度解决影响力最大化问题,本文选取的NVPA社区划分算法的性能要明显优于已知的3种从不同角度进行社区划分的典型算法。
为了验证上文提出的NVPA-IM算法的性能,本文将其与从社区中选取度最大节点的度中心算法(NVPA-DEG)、从社区中随机选取种子节点的算法(NVPA-R)以及从个体角度解决影响力最大化问题的贪婪算法(CELF++)进行对比分析。因为文献[2]中已经证明贪婪算法能够保证精度达到最优解的(1-1/e),而CELF++算法[5]是优化后的贪婪算法。相对于传统的贪婪算法,它将算法的运行效率提高了35%~55%。所以,在贪婪算法方面,本文选择CELF++算法,并将其影响收益作为算法精度对比分析的基准。
在LRF数据集上,基于IC模型,4种算法的影响收益对比结果如图3所示。
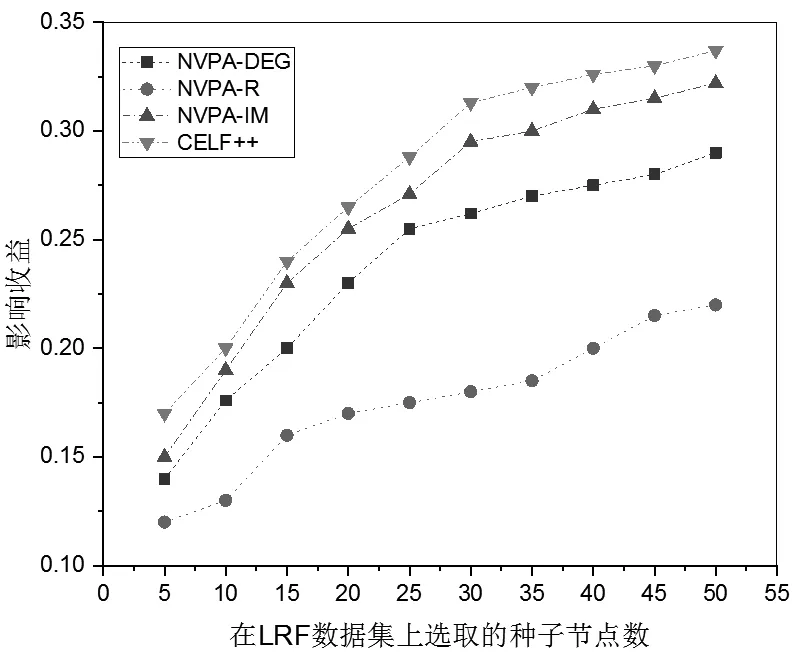
图3 不同影响力最大化算法在LRF数据集上的影响收益对比
如图3所示,NVPA-R算法获得的影响收益最差,CELF++算法获取的影响收益最好。相对于NVPA-DEG算法,NVPA-IM算法获取的影响收益更接近于CELF++算法,即NVPA-IM算法能够更准确地挖掘影响力最大的种子节点。在Facebook数据集上,4种算法的影响收益对比结果如图4所示。
如图4所示,在Facebook数据集上,以CELF++算法获取的影响收益为基准,NVPA-IM算法的影响收益要明显优于NVPA-DEG算法和NVPA-R算法。该算法只有极小的精度损失,这与在LRF数据集上NVPA-IM算法的表现相同。由以上分析可知,本文提出的种子节点选取算法相对于已有算法显著提高了算法精度。
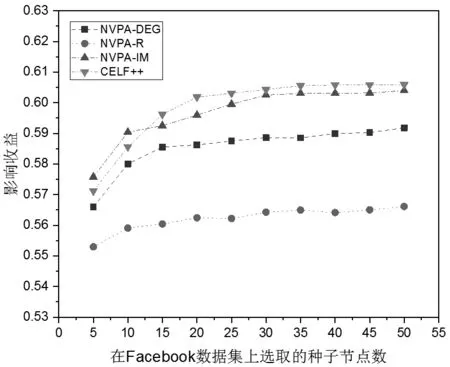
图4 不同影响力最大化算法在Facebook数据集上的影响收益对比
在验证算法效率阶段,本文将其和CELF++算法进行对比分析。为了保证算法的精度,CELF++算法为每个节点计算边际收益时,均需进行R次蒙特卡罗模拟,R一般取值为20 000。蒙特卡罗模拟的时间复杂度与网络中的边的数量成线性关系。所以,当网络的平均度较大、连边数量较多时,CELF++算法一般效率较低。而NVPA-IM算法主要的时间开销在社区划分阶段,由文献[7]实验证明,NVPA社区划分算法的效率较高。在本文实验中,基于IC传播模型,在LRF数据集上,当挖掘50个种子节点时,NVPA-IM算法只需要55 s,而CELF++算法需要729 s。可见,前一种算法用时只占到CELF++算法的7.5%。
3 结 语
本文提出了一种从社区层面解决影响力最大化问题的算法。基于社交网络的结构,本文首先使用NVPA算法对网络进行社区划分。考虑到划分的过程,节点之间的相似度受节点的m跳邻居节点影响。所以,本文设计了一个基于节点m跳及m跳以内的种子节点选取算法,从划分后的每个社区中挖掘出一个种子节点组成种子节点集。通过实验验证分析,在解决影响力最大化问题方面,与传统贪心算法相比,NVPA-IM算法以一定的算法精度为代价,显著提高了算法的运行效率。当然,该算法也存在一定不足,后续研究中,在影响力挖掘方面应该更加全面地结合网络和用户的各种属性特征进一步精确影响效果,贴近真实。
参考文献:
[1] Richardson M,Domingos P.Mining Knowledge-Sharing Sites for Viral Marketing[C].Proceedings of the Eighth ACM SIGKDD International Conference On Knowledge Discovery And Data Mining ACM,2002:61-70.
[2] Kempe D,Kleinberg J,Tardos É.Maximizing the Spread of Influence Through a Social Network[C].Proceedings of the ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining ACM,2003:137-146.
[3] Kempe D,Kleinberg J M,Tardos É.Maximizing the Spread of Influence through a Social Network[J].Theory of Computing,2015,11(04):105-147.
[4] Morone F,Makse H A.Influence Maximization Incomplex Networks Through Optimal Percolation[J].Nature,2015,524(7563):65-68.
[5] Goyal A,Lu W,Lakshmanan L V S.Celf++:Optimizing the Greedy Algorithm for Influence Maximization in Social Networks[C].Proceedings of the 20th International Conference Companion On World Wide Web ACM,2011:47-48.
[6] Tang Y,Xiao X,Shi Y.Influence Maximization:Nearoptimal Time Complexity Meets Practical Efficiency[C].Proceedings of the 2014 ACM SIGMOD International Conference On Management of Data ACM,2014:75-86.
[7] Liang X,Tang J,Pan L.A Neighborhood Vector Propagation Algorithm for Community Detection[C].Global Communications Conference(GLOBECOM),2014:2923-2928.
[8] Newman M E J.Modularity and Community Structure in Networks[J].Proceedings of the National Academy of Scie nces,2006,103(23):8577-8582.
[9] Leskovec J,Mcauley J J.Learning to Discover Social Circles in Ego Networks[C].Advances in Neural Information Processing Systems,2012:539-547.
[10] Lancichinetti A,Fortunato S,Radicchi F.Benchmark Graphs for Testing Community Detection Algorithms[J].Physical Review E,2008,78(04):046110.
[11] Newman M E J.Fast Algorithm for Detecting Community Structure in Networks[J].Physical Review E,2004,69(06):066133.
[12] Raghavan U N,Albert R,Kumara S.Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks[J].Physical Review E,2007,76(03):036106.
[13] Chen Y C,Zhu W Y,Peng W C,et al.CIM:Communitybased Influence Maximization in Social Networks[J].ACM Transactions on Intelligent Systems and Technology(TIST),2014,5(02):25.
