DIFFUSION VANISHING LIMIT OF THE NONLINEAR PIPE MAGNETOHYDRODYNAMIC FLOW WITH FIXED VISCOSITY∗

Zhonglin WU(吴忠林)

College of Mathematics and Statistics,Huanghuai University,Zhumadian 463000,China

E-mail:wuzhonglin03@126.com

Shu WANG(王术)

College of Applied Science,Beijing University of Technology,Beijing 100124,China

E-mail:wangshu@bjut.edu.cn

1 Introduction

In this article,we consider magnetic diffusion vanishing limit of the nonlinear pipe magnetohydrodynamic flow while viscosity is invariant.In our case,the fluids occupy an in finitely long pipe with circular cross-section of radius 1,with the x-axis being the axis of the pipe.We assume that the flow is parallel to the axis of the pipe all the time(therefore no component of the velocity in the radial direction),and the flow is periodic in x with period L for simplicity.Hence,the spatial domain is Q= Ω × [0,L],where Ω =(r,φ),0 ≤ r ≤ 1,φ ∈ [0,2π]is the unit disk and L is the horizontal period in the cylindrical coordinates φ being the azimuthal angle and r being the distance to the axis of the pipe.Throughout this article,we denote the solution of the MHD system with viscosity coefficient and magnetic diffusions by(uν,η,bν,η),satisfying the following system of equations:

where Δ is the Laplace operator;uν,η,pν,η,and bν,ηare the fluid velocity,the fluid pressure,and the magnetic field;α and β is the azimuthal velocity and magnetic field at the boundary.The incompressible viscous MHD system(1.1)–(1.3)in the whole space or with slip/no-slip boundary conditions were studied extensively,so there is a lot of literature on the well-posedness,regularity,and asymptotic limit topic;see[2–5,9,16,18–20]and therein references.Some authors have done a lot on some regularity criterions;see[3,4,9,18,19]and therein references.For example,when η1＞ 0,η2＞ 0,ν1＞ 0,and ν2＞ 0,the MHD system in the whole space and in the bounded domain with no-slip boundary condition for the velocity and with slip boundary condition for the magnetic field has a unique global classical solution for smooth initial data when space dimension d=2,but when d=3,there exists a global weak solution for a class of initial data,seeing[5,16].Xiao,Xin,and Wu investigate the solvability,regularity,and vanishing viscosity limit of the incompressible viscous MHD with slip without friction boundary conditions;see[20].Wu and Wang also consider zero viscosity and diffusion vanishing limit for the three-dimensional incompressible viscous and diffusive MHD system with Dirichlet boundary condition for the velocity and perfectly conducting wall boundary condition for the magnetic field;see[22].In[23],Han,Mazzucato and etc obtained viscosity vanishing limit for a class of Navier-Stokes equations using Prandtl boundary layers theory.Feng,Wand and etc also obtained the asymptotic behavior of global smooth solution for Bipolar compressible Navier-Stokes-Maxwell system from plasmas;see[25].Similarly,we point out that the viscosity vanishing limit,for the nonlinear pipe incompressible Magnetohydrodynamic flow with slightly viscous and diffusive,is a interesting problem because of the formation of the boundary layer;see[1,3,6–8,10–15,17]and related references.So far,we do not find any zero diffusion limit results for the nonlinear pipe incompressible Magnetohydrodynamic flow.

Setting η → 0 in(1.1)–(1.5),we have the following three-dimensional nonmagnetic MHD system with the fixed viscosity formally,

where n is the unit outer normal to∂Q.For simplicity,let us take the same initial condition for both(uν,η,bν,η)and(uν,0,bν,0),which is denoted by(u0(x),b0(x)).

The solutions of this special type of parallel pipe Magnetohydrodynamic flow that we investigate in this article satisfies the following assumptions:

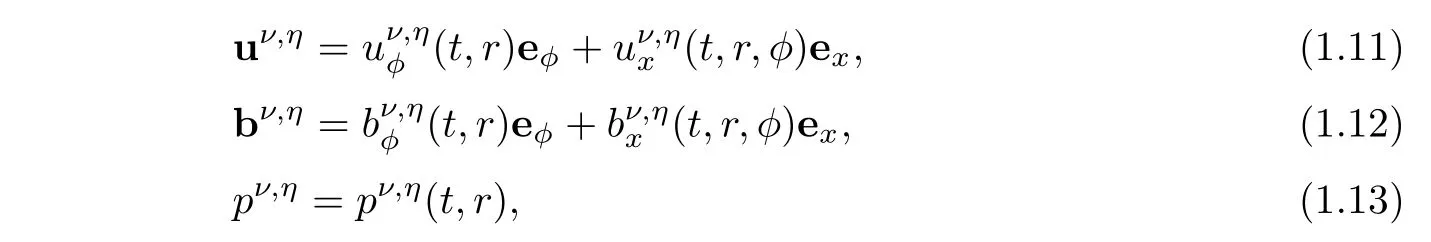
where uν,η,bν,η,and pν,ηare the fluid velocity,the magnetic field,and fluid pressure,respectively,and eφ,ex,erare the unit vector in the azimuthal direction,x direction,and radial direction,respectively.

Notice that such magnetohydrodynamic flow satisfy automatically the incompressibility condition,so the MHD system(1.1)–(1.5)is reduced to the following strongly nonlinear system under the assumptions(1.11)–(1.13):

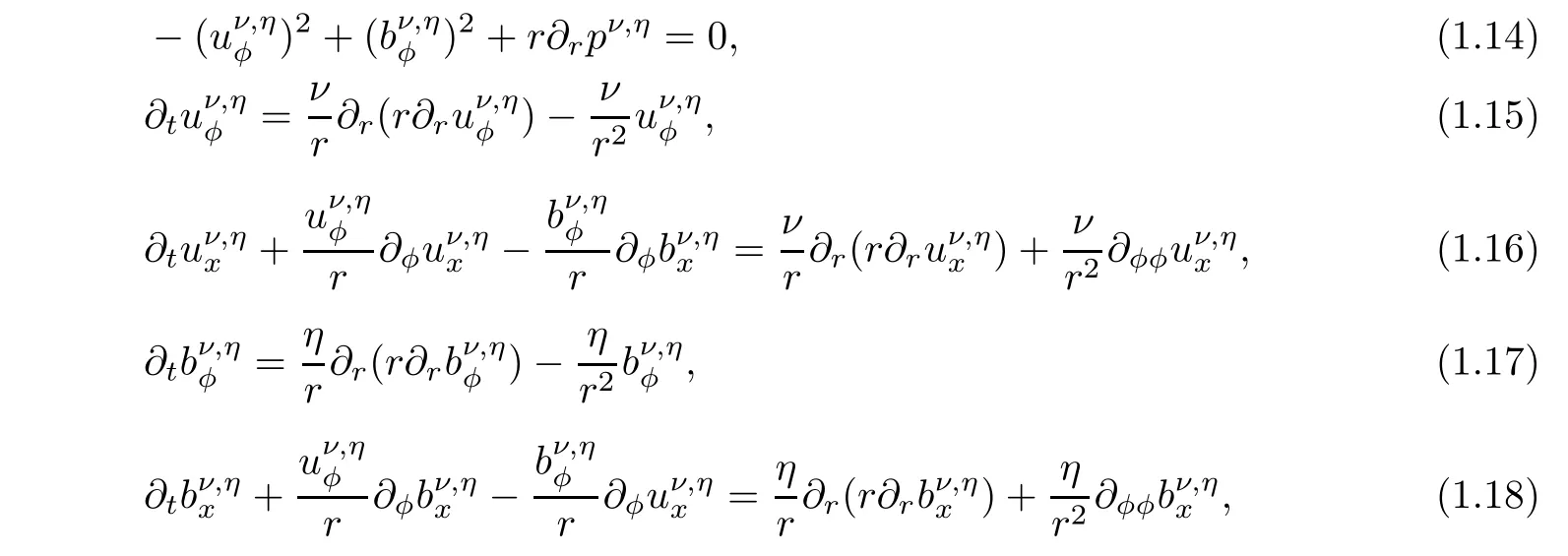
with the following initial and boundary data,

It is obvious that the pressure term pν,ηcan be uniquely recovered from equation(1.14).Furthermore,equations(1.15)–(1.18)form the following closed strongly coupled parabolic system in Cartesian coordinates,

with the following initial and boundary data(1.19)–(1.22).

Similar to assumptions(1.11)–(1.13),we also assume

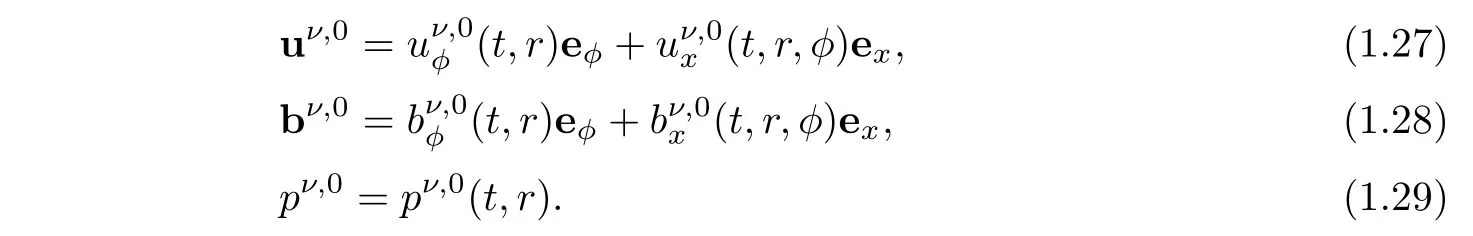
Thus,the nonmagnetic MHD system with the fixed viscosity(1.6)–(1.10)is reduced to the following system:

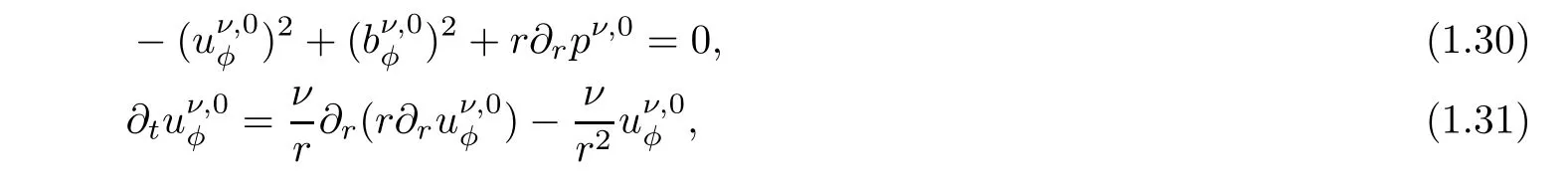
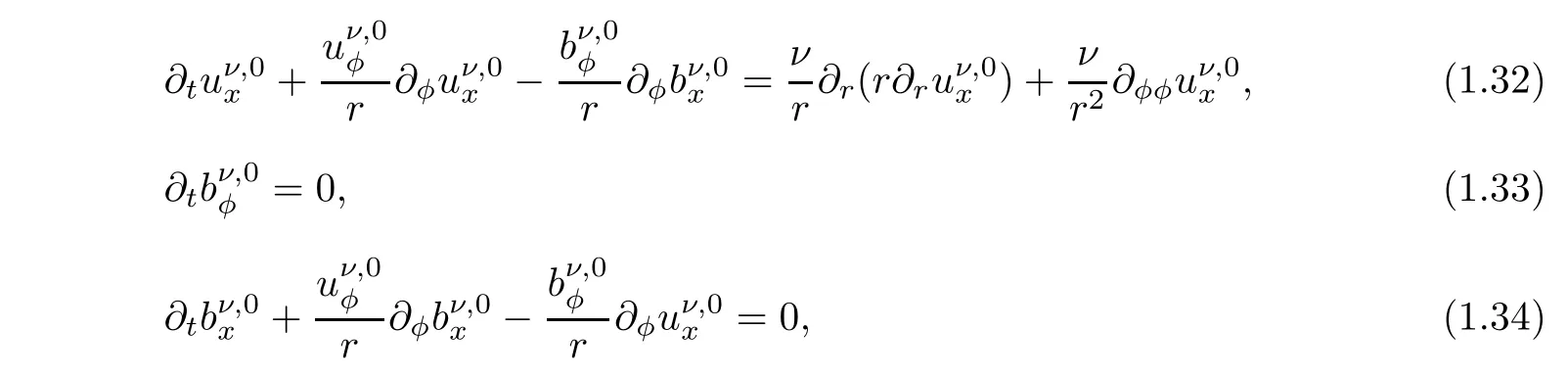
with initial condition:

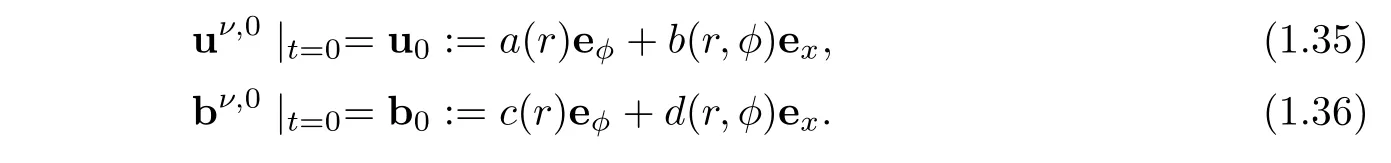
We observe that the no-penetration condition at the walls for the magnetic field of nonmagnetic solution is automatically satisfied in this case,but the boundary condition of the velocity fieldt is invariant,that is,

Because of the disparity of boundary conditions between the reduced MHD system(1.14)–(1.18)and the reduced nonmagnetic MHD system(1.30)–(1.34),a boundary layer must exist for the magnetic field,but there is not boundary layer for velocity field because viscosity coefficient is invariant.Outside of layer,the flow is expected to be well approximated by the inviscid solution(uν,0,bν,0).Inside the layer,a flow corrector is needed,which approximates(uν,η−uν,0,bν,η−bν,0).For leading order,the corrector θν,0is formally governed by the Prandtl-type equation(2.5)–(2.9)(see the next section for a formal derivation).The aim of this article is to investigate the mathematical validity of the Prandtl-type approximation for this special type of flow in a pipe.In other words,we need to prove that(uν,η− uν,0,bν,η− bν,0− θν,0)converges to zero in various norms.Our main result is the following theorem.

Theorem 1.1Under sufficient smoothness and compatibility assumptions on the initial and boundary data,for some constant c independent of the magnetic diffusions η,we have

We believe that the result proposed here is the first rigorous result for the Magnetohydrodynamic system in a nonlinear setting in a domain with curved boundaries.In particular,a novel coupled boundary layer and interior domain approach are used in order to derive the L∞(H1)estimate in our curved geometry.This approach allows us to easily handle the singularity at r=0 in(1.14)–(1.18).At the same time,it is not convenient to work in Cartesian coordinates near the boundary.The decay rates for the correctors is seen in[24].

It should be pointed out that the validity of the Prandtl theory proposed here is strictly under the assumption of the parallel pipe flow symmetry(1.11)–(1.13).We also remark that there are a lot of literature on boundary-layer analysis as well as the related vanishing viscosity limit problem associated with the Magnetohydrodynamic system equipped with different(non-Dirichlet)boundary conditions.For example,for the case of Navier-slip(and the simpler freeslip)boundary condition,there are many interesting works on the related vanishing viscosity limit as well as the analysis of the boundary layer.

This article is organized as follows.We present a formal derivation the equation for the leading-order corrector θν,0using the Prandtl-type asumption in Section 2.The well-posedness of the Prandtl-type boundary-layer system as well as appropriate decay properties is seen in[23].An approximate solution to the reduced nonmagnetic MHD system(1.14)–(1.18)is constructed in Subsection 2.2 using the inviscid solution(uν,0,bν,0)and the leading order boundary-layertype corrector θ0,η.The proofs of the zero diffusions results will be presented in Section 3 under various norms.

2 Prandtl-Type Corrector Equation and Approximate Solution

2.1 Prandtl-type corrector equation

According to the Prandtl boundary-layer theory,the diffusions solution and the zero diffusion solution are close to each other outside a boundary layer of thickness proportional toBut the diffusions solution must make a sharp transition to the zero diffusion in the boundary layer because of the disparity of the two kind flows at the boundary.Therefore,we assume that the solutions to the diffusions MHD system are as follows:

It is then convenient to work under the following domain for the corrector θν,0:

Substituting(2.1)–(2.3)into(1.14)–(1.18)and(1.19)–(1.22),utilizing the zero diffusion MHD system(1.30)–(1.34),and keeping the leading-order terms in η,we can obtain the following Prandtl-type equation,for the leading order of the boundary-layer profile(corrector)θν,0,

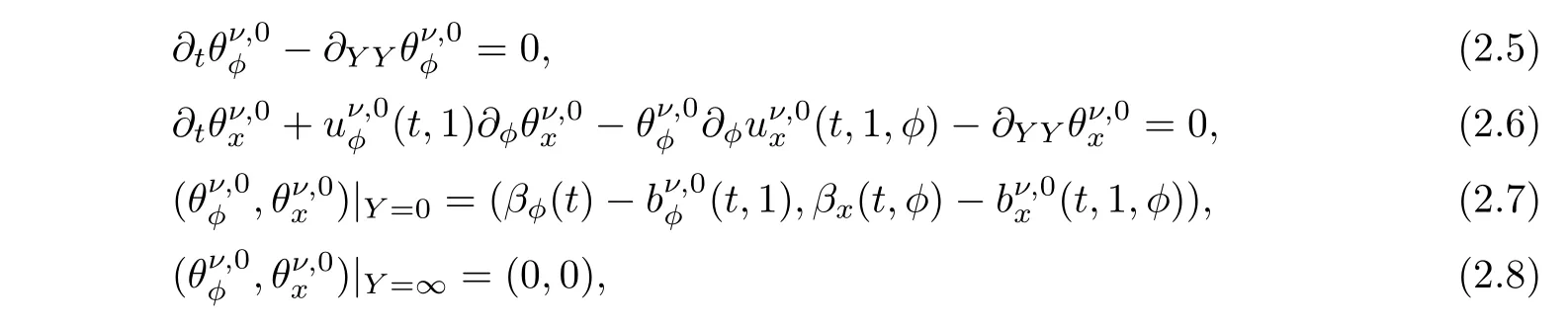
and the proof of the well-posedness and the decay as Y→∞of the solutionof the system are similar with the discussion of[23],under the appropriate compatibility conditions between the initial and boundary data.

At the same time,we notice that the leading-order correction qν,0to the pressure term satisfies

so we can conveniently take

2.2 Approximate Solution

With the corrector θν,0and the zero diffusion solution(uν,0,bν,0)in hand,now we can construct an approximate solution to the magnetic diffusion MHD system(1.14)–(1.18)under the given assumptions(1.11)–(1.13).

We introduce a cut-offfunction to ensure that the approximate solution of the magnetic diffusion MHD systemgiven below,satisfies the same boundary conditions as the magnetic diffusion MHD system solution(uν,η,bν,η).Let ρ(r)be a smooth function defined on[0,1]as follows

Because we consider the case that the viscosity coefficient ν is fixed,there is no boundary layer for velocity field,the approximate solution to the magnetic diffusion MHD system must have the following form because of(1.11)–(1.13):

By(2.11),we take the pressure to be

By verifying straightforwardly,we can observe that the approximate solutionconstructed above satisfies the following magnetic diffusion MHD system:

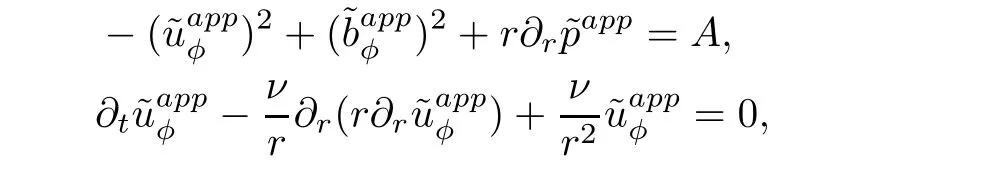
where the(small)extra body forces A−G are given by

The approximate solution satisfies the following expected boundary and initial conditions:

3 Error Estimates and Convergence Rates

We are now ready to prove our main result.As the convergence of(˜uapp,˜bapp)to(uν,η,bν,η)also implies the convergence of(uν,η− uν,0,bν,η− bν,0− θν,0)to zero because of the choice of the cut-offfunction ρ(r)in(2.12)and the decay property of the boundary-layer function θν,0,we introduce the error solution uerr=uν,η−˜uapp,berr=bν,η−˜bapp,with associated pressure perr=pν,η− papp.Because of the symmetry of the flow,the pressure appears only in the equations for the cross-sectional components of the velocity.The error solution satisfies the following system of equations:

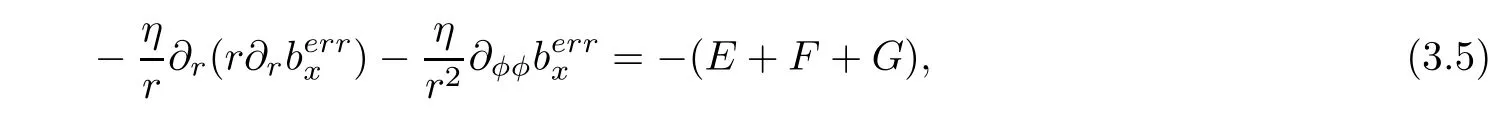
where the body forcing terms A through G are given in(2.16),and the initial data and boundary conditions are given as follows:

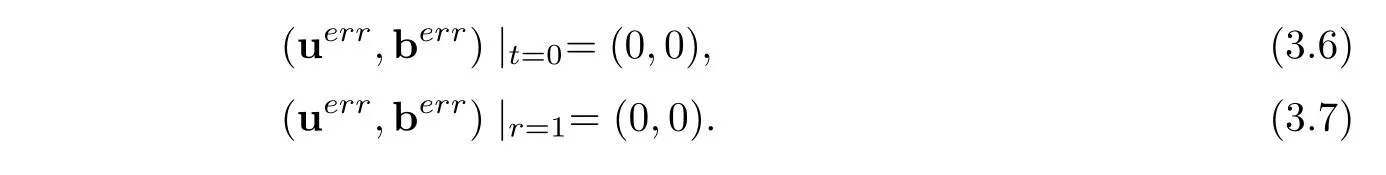
In this section,our aim is to prove that uerr,berr,and perrconverge to zero in different norms when the magnetic diffusion η approaches to zero.More precisely,we concentrate on proving the following result.

Theorem 3.1Suppose that the initial data(u0,b0)and the boundary data(α,β)satisfy the sufficient smoothness and compatibility,then there exist positive constants c independent of η,such that for any solution(uν,η,bν,η)of the system(1.14)–(1.22),we have

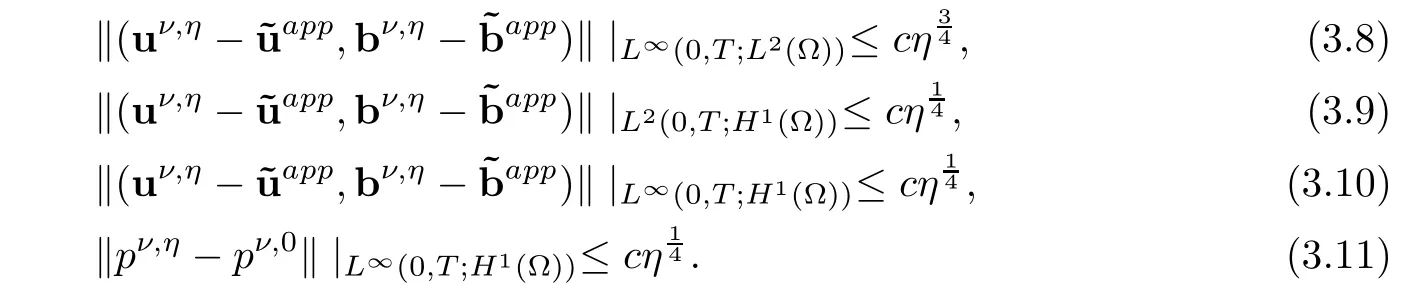
Theorem 1.1 follows from the theorem above and the decay property of the boundary-layer corrector θν,0.

The proof of Theorem 3.1 consists of several parts.We first prove that the extra body force terms are small.The L∞(L2)and L2(H1)estimates then follow directly.The L∞(H1)estimate needs a different approach,which are called as two steps methods,one near boundary,the other in the interior,proved by introducing a further cut-offfunction.The convergence of the pressure follows from the convergence of the velocity field and the magnetic field.

3.1 Smallness of the extra body forcing terms

We first give that the extra body forcing terms A−G in the right-hand side of the equations in(3.1)–(3.5)are all small in some appropriate sense.Here and below,c denotes a generic constant,independent of the viscosity η.Also,we note

Lemma 3.2Suppose that the initial data(u0,b0)and the boundary data(α,β)are given by sufficient smoothness and compatibility,then we have the following estimates for A−G given in(3.1)–(3.5):

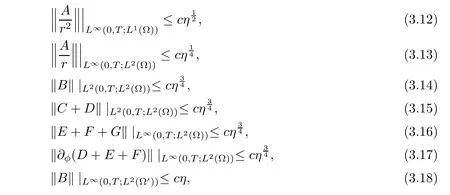
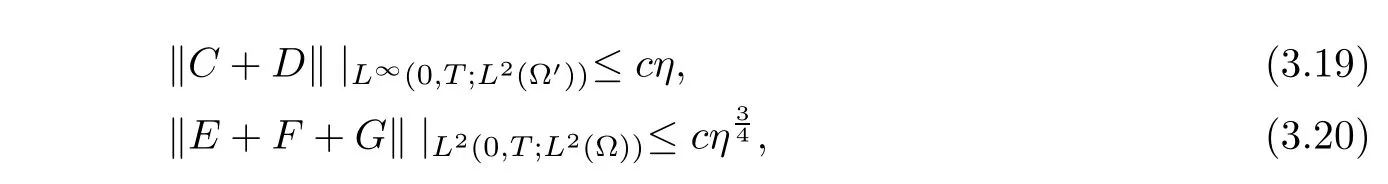
for any subset Ω′of Ω such that the closure Ω′⊂ Ω.

ProofThe proof of(3.12)–(3.20)is easy;we omit it(also see[23]).

3.2 The L∞(L2)and L2(H1)convergence

We notice that the error solution error solutionsatisfies the systems(3.1)–(3.5)and(3.6)–(3.7).So,we feel that it will be convenient here to work in Cartesian rather than cylindrical coordinates.We observe that equations system(3.2)–(3.5),together with the initial-boundary conditions(3.6)–(3.7),form a closed strongly coupled parabolic system,which can be rewritten in Cartesian coordinates as

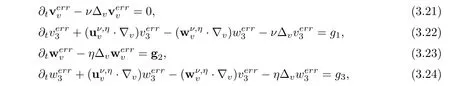
where verr≡uerrand werr≡berrin Cartesian coordinates,that is,

with

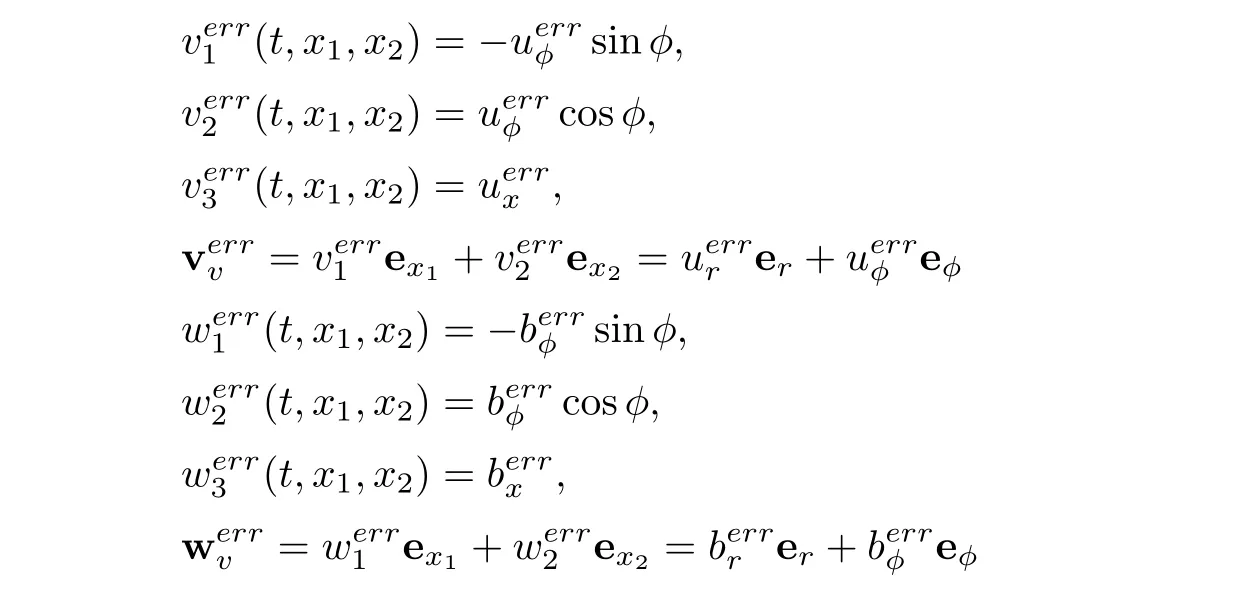
together with homogeneous initial and boundary conditions

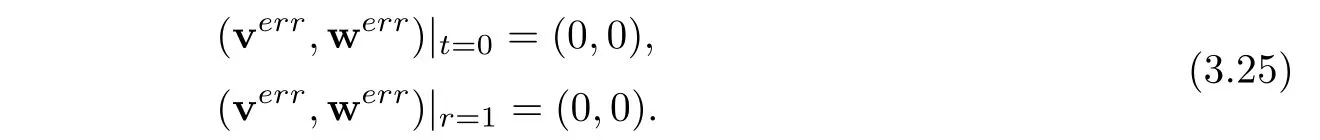
The forcing terms g1−g3are given as follows:

We observe that the cross-sectional componentandsatisfies,respectively,a twocomponent(scalar)heat equation(3.21)and(3.23).Using standard energy estimates and the maximum principle together with the estimates(3.15)and(3.19)in Lemma 3.1,we can obtain

We also observe that the termin g3,andin g4can be rewritten,respectively,as

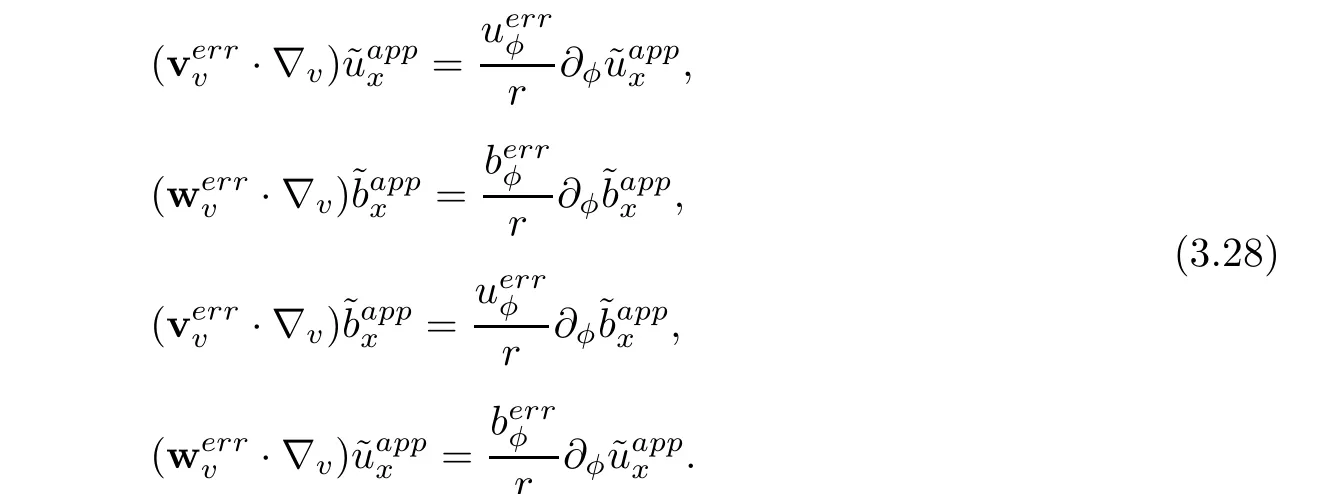
We assert from the definitions ofandgiven in(2.13),the decay properties of the corrector θ0,η,and the regularity of solutions to the zero diffusion MHD system,that

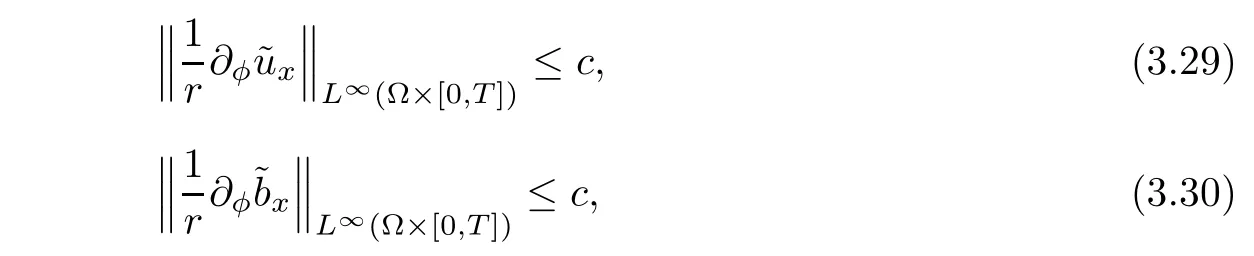
with a constant c depending on ‖u0‖H3(Ω),‖b0‖H3(Ω),‖α‖L∞(0,T;H3(Ω)),‖β‖L∞(0,T;H3(Ω)),but independent of η.Therefore,we can obtain the following uniform estimates by(3.27)and(3.29)–(3.30),

Applying the energy argument to Equation(3.22)and(3.24),we can obtain

3.3 The L∞(H1)convergence

In this section,we concentrate on the derivation of the L∞(H1)estimate forgiven that an L∞(H1)estimate ofwas already obtained in(3.32).

We apply the two-step approach for it.Firstly,we give an estimate near the boundary based on the better control we have on tangential derivatives even in the presence of a boundary layer;secondly,we will obtain a standard interior energy estimate away from the boundary layer.

3.3.1 Estimate near the boundary

In order to separate the boundary layer from the interior,a further cut-offfunction ϕb(r)is introduced with an appropriately chosen support in Ω,which is specified as follows,

with homogeneous initial and boundary conditions:

Firstly,we multiply Equation(3.34)by −∂φφUb·r and Equation(3.35)by −∂φφBb·r,and then integrate it in r and φ,therefore we can obtain Furthermore,we have

Using Grönwall inequality and estimate,we obtain

At the same time,we also have

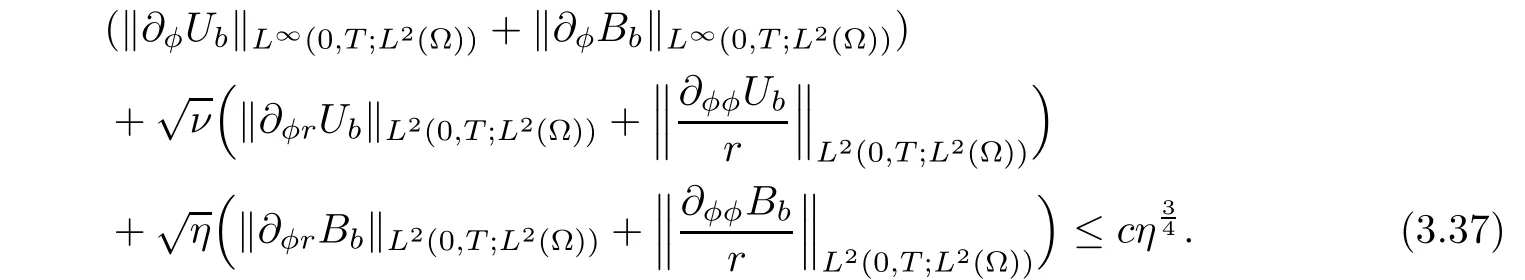
Secondly,we multiply Equation(3.34)byand integrate it by parts,then we have

Using estimates(3.28),(3.29),(3.30),Young inequality,and Grönwall inequality,we can obtain

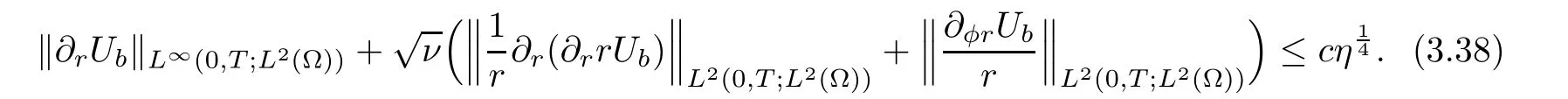
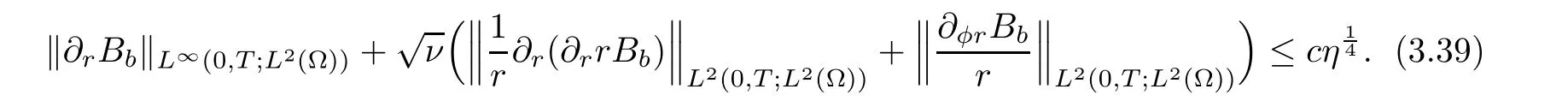
3.3.2 Interior estimate

In this subsection,we concentrate on the estimates of the interior of Ω.For this goal,set ϕi(r)=1−ϕb(r),which satisfies

with the homogeneous initial and boundary conditions,

Multiplying Equation(3.41)by Uiand integrating the resulting equation over Ω,we obtain

Using the same way for Equation(3.42),we also obtain

Using the same way for Equation(3.42),we also obtain

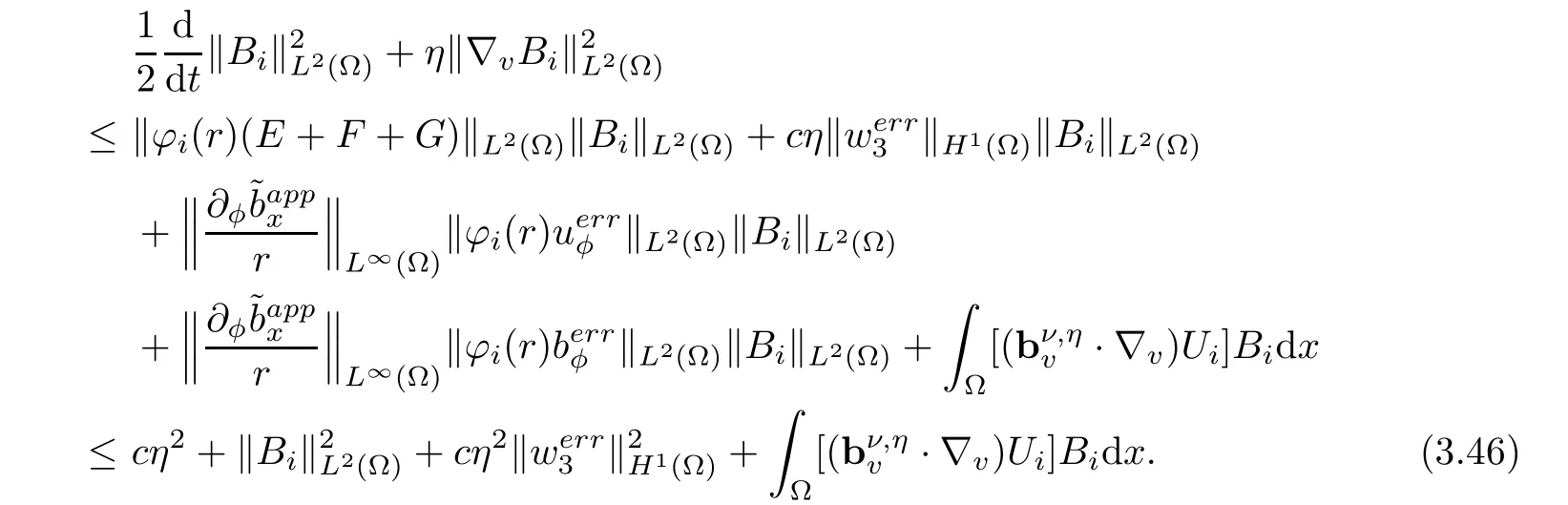
Together(3.44)with(3.46)and thanks to the Grönwall inequality,we have

Next,multiplying by−△vUion both sides of Equation(3.41)and integrating the resulting equation over Ω,we can also obtain

We can deal with the last two term as follows:

and

By introducing(3.49)and(3.50)back into(3.48),applying Young inequality and(3.28)–(3.30),we finally obtain

Thanks for Grönwall inequality and(3.46)–(3.47),we have

similarly,multiplying by−△vBion the both sides of Equation(3.42)and integrating the resulting equation over Ω,we can also obtain

Combining(3.37),(3.38),(3.39),(3.47),(3.51)and(3.52),we obtain

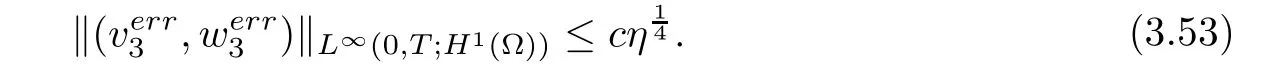
3.4 Convergence of the pressure

We first notice the following calculus formula for a vector function u=v(r)eφ

Then,by calculas simply from Equation(3.1),we obtain

Next,we integrate Equation(3.1)to give that,assuming perr(1)=0,

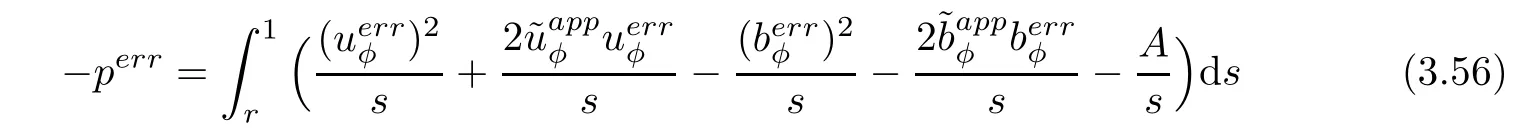
Therefore,applying estimates(3.12)and(3.27),we have

[1]Alekseenko S N.Existence and asymptotic representation of weak solutions to the flowing problem under the condition of regular slippage on solid walls.Siberian Math J,1994,35:209–230

[2]Biskamp D.Nonlinear Magnetohydrodynamics.Cambridge,UK:Cambridge University Press,1993

[3]Cao C S,Wu J H.Global regularity for the 2D MHD equations with mixed partial dissipation and magnetic diffusion.Advances in Math,2011,226:1803–1822

[4]Chen Q L,Miao C X,Zhang Z F.The Beale-Kato-Majda criterion for the 3D magnetohydrodynamics equations.Comm Math Phys,2007,275:861–872

[5]Duvaut G,Lions J L.Inéquation en themoélasticite et magnétohydrodynamique.Arch Ration Mech Anal,1972,46:241–279

[6]E W.Boundary layer theory and the zero viscosity limit of the Navier-Stokes equations.Acta Math Sin(English Series),2000,16:207–218

[7]E W,Engquist B.Blowup of solutions of the unsteady Prandtl’s equation.Comm Pure Appl Math,1997,50:1287–1293

[8]Grenier E,Masmoudi N.Ekman layers of rotating fluids,the case of well prepared initial data.Comm P D E,1997,22:953–975

[9]He C,Xin Z P.Partial regularity of suitable weak solutions to the incompressible magnetohydrodynamic equations.J Funct Anal,2005,227:113–152

[10]Kato T.Nonstationary flow of viscous and ideal fluids in R3.J Funct Anal,1972,9:296–305

[11]Ladyzhenskaya O A.The Mathematical Theory of Viscous incompressible Flows.2nd ed.New York:Gordon and Breach,1969

[12]Lions J L.Méthodes de Résolution des Problémes x Limites Non Líeaires.Paris:Dunod,1969

[13]Masmoudi N.Ekman layers of rotating fluids:The case of general initial data.Comm Pure and Appl Math,2000,53:432–483

[14]Sammartino M,Ca flisch R E.Zero viscosity limit for analytic solutions of the Navier-Stokes equations on a half space.I.Existence for Euler and Prandtl equations.Comm Math Phys,1998,192:433–461

[15]Sammartino M,Ca flisch R E.Zero viscosity limit for analytic solutions of the Navier-Stokes equations on a half space.II.Construction of Navier-Stokes solution.Comm Math Phys,1998,192:463–491

[16]Sermange M,Temam R.Some mathematical questions related to the MHD equations.Comm Pure Appl Math,1983,36:635–664

[17]Temam R,Wang X.Boundary layers associated with incompressible Navier-Stokes equations:The noncharacteristic boundary case.J DiffEqns,2002,179:647–686

[18]Wu J H.Vissous and inviscid magneto-hydrodynamics equations.Journal D’Analyse Mathematique,1997,73:251–265

[19]Wu J H.Regularity criteria for the generalized MHD equations.Comm Partial DiffEqns,2008,33:285–306

[20]Xiao Y L,Xin Z P,Wu J H.Vanishing viscosity limit for the 3D magneto-hydrodynamic system with a slip boundary condition.J Funct Anal,2009,257:3375–3394

[21]Xin Z P.Viscous boundary layers and their stability.I.J Partial Differential Equations,1998,11:97–124

[22]Wu Z L,Wang S.Zero viscosity and diffusion vanishing limit of the incompressible magnetohydrodynamic system with perfectl conducting wall.Non Anal:Real World Appl,2015,24:50–60

[23]Han D Z,Mazzucato A L,et al.Boundary layer for a class of nonlinear pipe flow.J DiffEqns,2012,252:6387–6413

[24]Xin Z,Yanagisawa T.Zero-viscosity limit of the linearized Navier-Stokes equations for a compressible viscous fluid in the half-plane.Comm Pure Appl Math,1999,52(4):479–541

[25]Feng Y H,Wang S,Li X.Asymptotic behavior of global solutions for bipolar compressible Navier-Stokes maxwell system from plasmas.Acta Mathematica Scientia,2015,35B(5):955–969