MULTIPLICITY OF SOLUTIONS OF WEIGHTED(p,q)-LAPLACIAN WITH SMALL SOURCE∗
2018-05-05HuijuanSONG宋娟
Huijuan SONG(宋娟)
College of Mathematics and Informational Science,Jiangxi Normal University,Nanchang 330022,China
E-mail:songhj@jxnu.edu.cn
Jingxue YIN(尹景学)
School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China
E-mail:yjx@scnu.edu.cn
Zejia WANG(王泽佳)†
College of Mathematics and Informational Science,Jiangxi Normal University,Nanchang 330022,China
E-mail:zejiawang@jxnu.edu.cn
1 Introduction
The purpose of this article is to study the multiplicity of solutions for the system with small sources:

where Ω ⊂ RNis a bounded domain with smooth boundary∂Ω,N ≥ 2,1< r< p< ∞,1 < s< q< ∞;h1(x)and h2(x)are allowed to have“essential” zeroes at some points in Ω;d(x)and f(x)can be very small,in particular,small supports and sign changing for d(x)and f(x)are permitted and the terms Gu(x,u,v)and Gv(x,u,v)will be considered as high-order perturbations of the small sources d(x)|u|r−2u and f(x)|v|s−2v with respect to(u,v)near the origin respectively.
For the semilinear case of single equation

where r∈ (1,2)and λ > 0,existence of in finitely many solutions has attracted much attention and has been extensively studied in the last three decades.For example,in[1]Ambrosetti-Badiale obtained in finitely many solutions of(1.2)with negative energy when g(x,u)≡0,using a dual variational formulation.Ambrosetti-Brezis-Cerami[2]and Garcia-Peral[3]proved that(1.2)has in finitely many solutions with negative energy provided that g(x,u)=|u|m−2u,m ∈ (2,2∗],where 2∗=2N/(N −2)for N ≥ 3 and 2∗= ∞ for N=1,2,and 0< λ < λ∗for some finite λ∗.For 2 < m < 2∗,Bartsch-Willem[4]removed the restriction on λ and obtained in finitely many solutions under the assumptions that g(x,u)= µ|u|m−2u,m ∈ (2,2∗),µ ∈ R,and λ > 0.It should be noted that in all quoted articles above,the global property of g(x,u)for u large was used in an essential way to derive multiplicity results of solutions with negative energy.It was Wang[5]who first observed that existence of in finitely many solutions of(1.2)with negative energy relies only on local behavior of the equation and assumptions on g(x,u)only for small u are required.More precisely,he proved that if 1 < r< 2,g ∈ C(Ω ×(−δ,δ),R)for some δ> 0,g is odd in u and g(x,u)=o(|u|r−1)as|u|→ 0 uniformly in x ∈ Ω,then for all λ>0,(1.2)has a sequence of weak solutions with negative energy,thus improving all the previous results.It is worth pointing out that positivity λ>0 plays a crucial role in his argument.Recently,Guo[6]and Jing-Liu[7]considered the following problem

where d∈ C(Ω)is allowed to change sign,more exactly,

In[6],Guo proved that if 1 < r < 2,(1.4)holds,g ∈ C(Ω × (−δ,δ),R)for some δ> 0,g is odd in u and g(x,u)=o(|u|)as|u|→ 0 uniformly in x∈Ω,then(1.3)has a sequence of nontrivial solutions whose L∞-norms converge to zero.Jing-Liu[7]removed the oddness of the perturbation term g,and assumed that g ∈ C(Ω×(−δ,δ),R)for some δ> 0,g(x,u)=o(|u|τ−1)as|u|→0 uniformly in x∈Ω,where 2+N(2−r)/r<τ≤2∗for N ≥3 and 2+N(2−r)/r< τ for N=1,2.Chung[8]further showed the existence of in finitely many solutions of the system(1.1)with linear principal parts,that is,

where the diffusion coefficients h1and h2are from the space(H)σwith σ ∈ [0,∞),defined by


hold uniformly in x ∈ Ω for some θ,τ≥ 0.The degeneracy of problem(1.1)is considered in the sense that the measurable,non-negative diffusion coefficient h ∈ (H)σis allowed to have at most a finite number of zeroes at some points in Ω.For more details,we refer the reader to[9].The physical motivation of the assumption h∈(H)σis related to the modeling of reaction diffusion processes in composite materials,occupying a bounded domain Ω,in which at some points they behave as “perfect” insulators and so it is natural to assume that h(x)vanishes at these points(see[10]).
Motivated by the above mentioned works,in this article,we aim to extend the result to system(1.1)with the principal parts consisting of weighted(p,q)-Laplacian without the restriction r=s.Just as the interests in[5,6,8],we will establish the existence of a sequence of solutions with negative energy for system(1.1).
This article is organized as follows.In Section 2,we present some preliminaries and the main result of this article,which will be proved in Section 3.
2 Main Result
In this section,we formulate the main result of this article.Before that,we give the fundamental hypotheses and the definition of solutions to system(1.1).
Throughout this article,we always assume that the following conditions hold:
(H1)h1∈ (H)αfor some αand h2∈ (H)βfor some β ∈

hold uniformly in x ∈ Ω,where γ and δ are some nonnegative constants such that

For the completeness and the convenience of the reader,we recall that the weighted Sobolev spacewhere 1< m < ∞ and h∈ (H)σfor someis defined as the closure of(Ω)with respect to the norm

for which,we have the following embedding result(see[11]).
Lemma 2.1Let Ω be a bounded domain in RN,N≥2,1<m<∞and h∈(H)σfor someThen,the following properties hold:
(ii)If 1<m≤N+σ,then the embeddingis compact for every r ∈ [1,m∗σ),whereif 1< m < N+σ and
(iii)If m>N+σ,then the embeddingis compact.
According to the assumption(H1),the space setting for our problem is naturally the product space

equipped with the norm ‖ω‖H= ‖u‖h1+ ‖v‖h2.Now,we can give the definition of solutions to system(1.1).
Definition 2.2We say that ω =(u,v)∈ H is a weak solution to system(1.1)if‖u‖L∞(Ω)< ρ1,‖v‖L∞(Ω)< ρ2,and the identity

Our main result of this article reads as follows.
Theorem 2.3Let 1< r< p< ∞,1< s< q< ∞,and the conditions(H1)–(H3)be fulfilled.Then,system(1.1)has in finitely many solutions ωksuch that ‖ωk‖L∞(Ω)→ 0 as k→∞.
We conclude this section by the following lemma,which will play an essential role in our arguments.
Lemma 2.4([12]) Let X be a Banach space and Φ ∈ C1(X,R).Assume that Φ satisfies the(PS)condition,being even and bounded from below,and Φ(0)=0.If for any k ∈ N,there exist a k-dimensional subspace Xkof X and ρk> 0 such thatwhere Sρ={ω ∈ X|‖ω‖= ρ},then at least one of the following conclusions holds:
(i)There exists a sequence of critical points{ωk}satisfying Φ(ωk)< 0 for all k and ‖ωk‖ → 0 as k→∞;
(ii)There exists r>0 such that for any 0<a<r,there exists a critical point ω such that‖ω‖ =a and Φ(ω)=0.
3 Proof of Main Result
In this section,we prove Theorem 2.3,following the approach introduced in[5].Denote by λ1the positive principal eigenvalue of the following Dirichlet problem
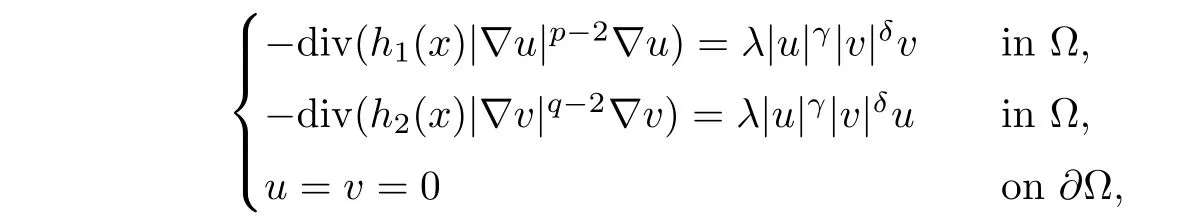
where γ,δ≥ 0 satisfy(2.1),seeing[13]for p=q=2 and[14]for general p,q.Namely,

As in[5,6,8],we first modify G so that Guand Gvare well-defined for all(x,u,v)∈×R2.
Proposition 3.1Let condition(H3)hold.Then,for any λ ∈ (0,λ1),there exist∈(0,ρ1/2),∈ (0,ρ2/2),and∈ C1(× R2,R)such thateG is even in(u,v)and satisfies


for all(x,u,v)∈Ω×R2;

for all(x,u,v)∈Ω×R2.
ProofFirst,given λ ∈ (0,λ1),choose ε such that
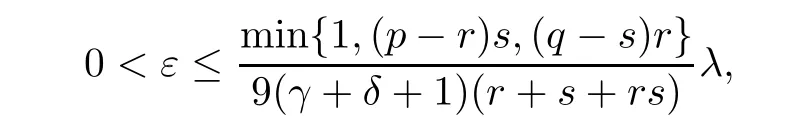
for which,by(H3),there exist∈ (0,ρ1/2)and∈ (0,ρ2/2)such that for any|u| ≤|v|≤and x ∈ Ω,

and then

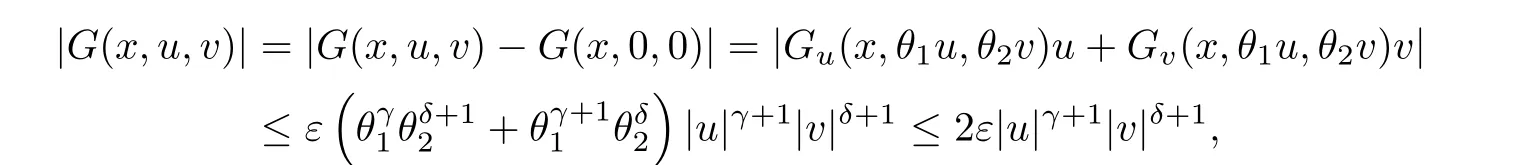
where 0 < θ1,θ2< 1.
Next,setting η(t1,t2)= φ(t1)ψ(t2)in which φ,ψ ∈ C∞(R),they are even and satisfy


Define


for all(x,u,v)∈Ω×R2,that is,(3.4)holds.Finally,a direct calculation shows that ifthen


which together with the choice of ε proves(3.3).Thus,the proof is completed.
Now,we are ready to prove Theorem 2.3.
Proof of Theorem 2.3Without loss of generality,we may assume that 1<p<N+α and 1<q<N+β.Consider the modified elliptic problem

and its associated functional

From the construction ofeG,it is easy to see that J∈C1(H),J is even and J(0)=0.In the sequel,for the sake of clarity,we divide the proof of the theorem into several steps.
Step 1We claim that the functional J is coercive and bounded from below in H.Let ω=(u,v)∈H.Then,in virtue of(3.4)and(3.1),using Lemma 2.1,we have

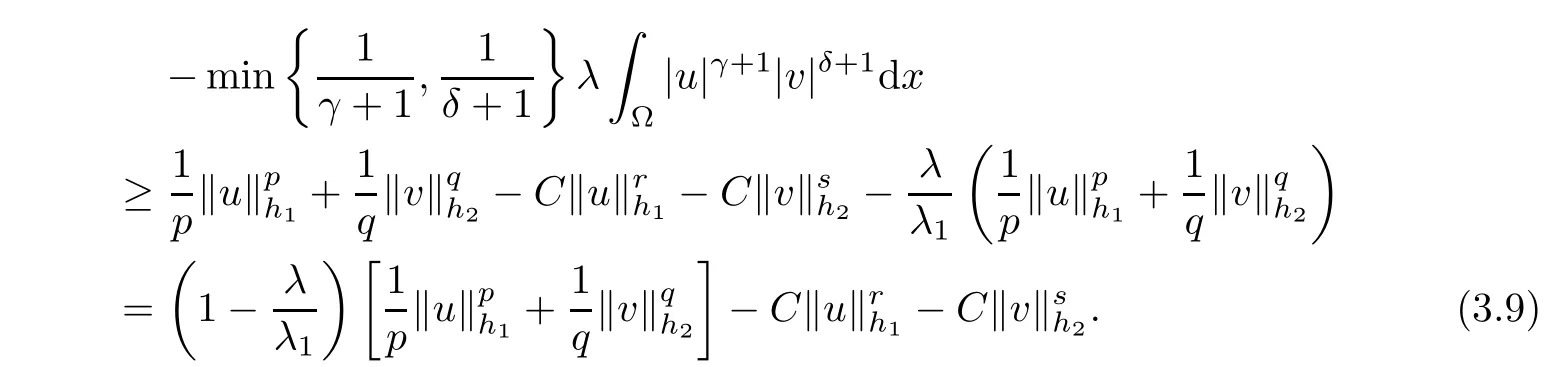
As λ ∈ (0,λ1),1< r< p,and 1 < s< q,by applying Young’s inequality to(3.9),we conclude the claim.
Step 2We show that the functional J satisfies the Palais-Smale condition in H.Let{ωn}={(un,vn)}be a(PS)sequence,namely,

where M is independent of n and H−1is the dual space of H.Then,{ωn}is uniformly bounded in H.Thus,by Lemma 2.1,there exists a subsequence of{ωn},denoted by{ωnj}and ω0=(u0,v0)∈ H,such that

and


using(3.10),(3.11),and(3.12),we deduce that

as j→∞.That is to say

and

On the other hand,an application of Hölder’s inequality shows that

Using the elementary inequalities
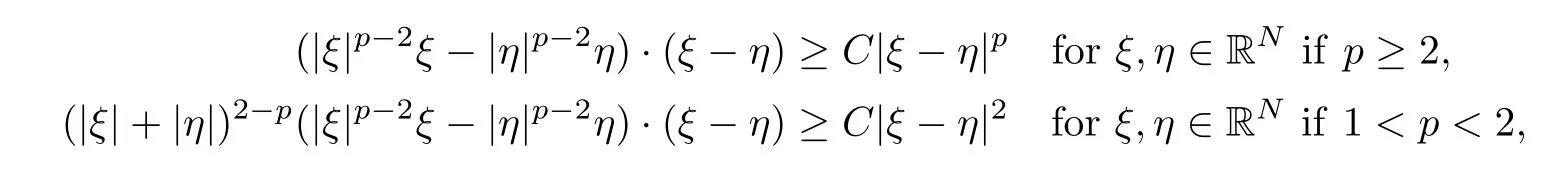
and the fact that{unj}is bounded,it is easy to see that

Hence,unj→u0in(Ω,h1)as j→ ∞ and similarly,vnj→v0in(Ω,h2)as j→ ∞.
Step 3We prove that for any given positive integer k,there exist a k-dimensional subspace Hkand an associated positive number ρk,such that

where Sρ={ω ∈ H:‖ω‖H= ρ}.By(H2),without loss of generality,we may assume that/= ∅ and moreover,d(x)≥ d0> 0 onThen,for any given positive integer k,we can choose k manually disjoint open ball Bj⊂BR(x0),define ξj∈(Bj)such that‖ξj‖h1=1,j=1,2,···,k,and set

Now,let ω0∈ Hk∩ Sρkbe fixed,where ρkis chosen such that

Then,according to the definition of Hk,there uniquely exist real numbers a1,a2,···,ak,such that

Thus,

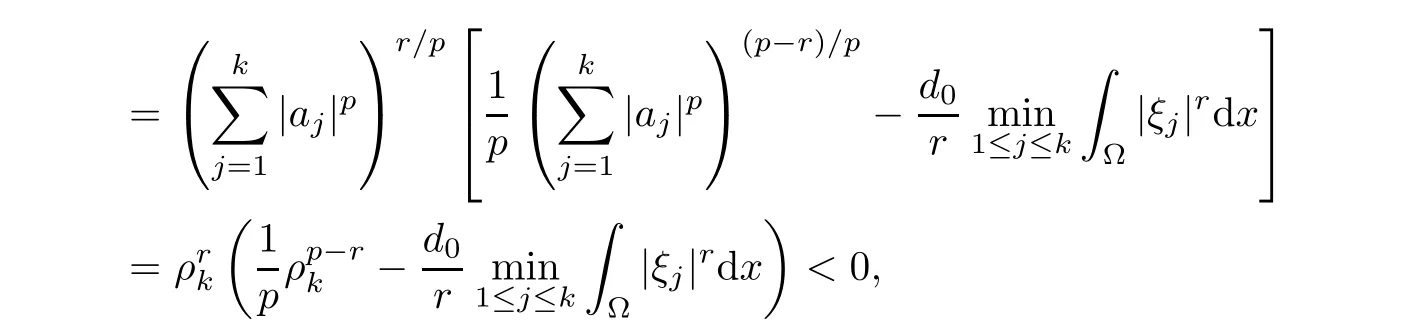
which together with the arbitrariness of ω0shows(3.13).
Step 4It is obtained that J(ω)=0 and DJ(ω)=0 if and only if ω =(0,0).Evidently,J((0,0))=0 and DJ((0,0))=0.Conversely,if both J(ω)=0 and DJ(ω)=0 hold for some ω=(u,v)∈H,then

and

Thus,

Furthermore,on one hand,using(3.1),we have

On the other hand,by virtue of(3.3),

From(3.14)–(3.16)and 0 < λ < λ1,it follows that ω =(0,0),as required.
Step 5We complete the proof of Theorem 2.3.Now,we appeal to Lemma 2.4 to obtain in finitely many solutions{ωk(=(uk,vk))}for(3.7)such that‖ωk‖H→ 0 as k → ∞.A standard regularity argument(see[14])then shows that‖ωk‖L∞(Ω)→ 0 as k → ∞,and therefore for k large ωkare solutions of(1.1).Thus,the proof is completed.
[1]Ambrosetti A,Badiale M.The dual variational principle and elliptic problems with discontinuous nonlinearities.J Math Anal Appl,1989,140(2):363–373
[2]Ambrosetti A,Brezis H,Cerami G.Combined effects of concave and convex nonlinearities in some elliptic problems.J Funct Anal,1994,122(2):519–543
[3]Garcia Azorero J P,Peral Alonso I.Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term.Trans Amer Math Soc,1991,323(2):877–895
[4]Bartsch T,Willem M.On an elliptic equation with concave and convex nonlinearities.Proc Amer Math Soc,1995,123(11):3555–3561
[5]Wang Z Q.Nonlinear boundary value problems with concave nonlinearities near the origin.Nonlinear DiffEqu Appl(NoDEA),2001,8(1):15–33
[6]Guo Z J.Elliptic equations with indefinite concave nonlinearities near the origin.J Math Anal Appl,2010,367(1):273–277
[7]Jing Y T,Liu Z L.In finitely many solutions of p-sublinear p-Laplacian equations.J Math Anal Appl,2015,429(2):1240–1257
[8]Chung N T.Existence of in finitely many solutions for degenerate and singular elliptic systems with indefinite concave nonlinearities.Electron J DiffEqu,2011,2011(30):1–12
[9]Caldiroli P,Musina R.On a variational degenerate elliptic problem.Nonlinear DiffEqu Appl(NoDEA),2000,7(2):187–199
[10]Dautray R,Lions J L.Mathematical Analysis and Numerical Methods for Science and Technology,Vol.1:Physical Origins and Classical Methods.Berlin:Springer-Verlag,1990
[11]Anh C T,Ke T D.Long-time behavior for quasilinear parabolic equations involving weighted p-Laplacian operators.Nonlinear Anal,2009,71(10):4415–4422
[12]Liu Z L,Wang Z Q.On Clark’s theorem and its applications to partially sublinear problems.Ann I H Poincaré-AN,2015,32(5):1015–1037
[13]Zographopoulos N B.On a class of degenerate potential elliptic system.Nonlinear DiffEqu Appl(NoDEA),2004,11(2):191–199
[14]Zographopoulos N B.On the principal eigenvalue of degenerate quasilinear elliptic systems.Math Nachr,2008,281(9):1351–1365
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- EXISTENCE AND BLOW-UP BEHAVIOR OF CONSTRAINED MINIMIZERS FOR SCHRÖDINGER-POISSON-SLATER SYSTEM∗
- STABILITY AND BIFURCATION ANALYSIS OF ADELAYED INNOVATION DIFFUSION MODEL∗
- ON A CLASS OF DOUGLAS FINSLER METRICS∗
- SOLUTIONS TO BSDES DRIVEN BY BOTH FRACTIONAL BROWNIAN MOTIONS AND THE UNDERLYING STANDARD BROWNIAN MOTIONS∗
- LIOUVILLE THEOREM FOR CHOQUARD EQUATION WITH FINITE MORSE INDICES∗
- THE GLOBAL ATTRACTOR FOR A VISCOUS WEAKLY DISSIPATIVE GENERALIZED TWO-COMPONENT µ-HUNTER-SAXTON SYSTEM∗
