MULTIPLICITY AND CONCENTRATION BEHAVIOUR OF POSITIVE SOLUTIONS FOR SCHRÖDINGER-KIRCHHOFF TYPE EQUATIONS INVOLVING THE p-LAPLACIAN IN RN∗

Huifang JIA(贾)Gongbao LI(李工宝)

Hubei Key Laboratory of Mathematical Sciences and School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China E-mail:hf jia@mails.ccnu.edu.cn;ligb@mail.ccnu.edu.cn

1 Introduction

In this article,we consider the multiplicity and concentration behavior of positive solutions for the following Schrödinger-Kirchhofftype problem

involving the p-Laplacian,where 1＜p＜N,M:R+→R+,V:RN→R+are continuous function,∈is a small positive parameter,and Δpu=div(|∇u|p−2∇u)is the p-Laplacian of u.We assume that the potential V satisfies

(V1)V∈C(RN,R)and

(V2)for each δ＞ 0,there is an open and bounded set Λ = Λ(δ) ⊂ RNdepending on δ such that

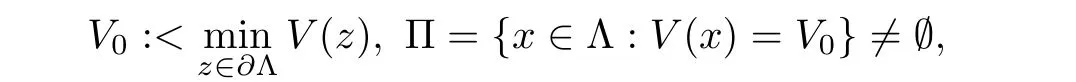
and

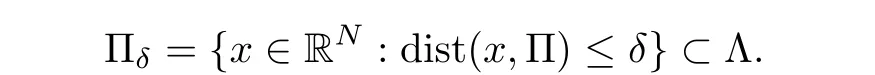
Problem(Q∈)is of nonlocal because of the presence of the termwhich implies that the equation in(Q∈)is no longer a pointwise identity.

Problem(Q∈)is a natural extension of two classes of problems of great importance in applications,namely,Kirchhofftype problems and Schrödinger type problems.

(a)When ∈=1,p=2,and V=0,problem(Q∈)becomes the following problem

which represents the stationary case of Kirchhoffmodel for small transverse vibrations of an elastic string by considering the effects of the changes in the length of the string during the vibrations.

(b)When M ≡1 and p=2,(Q∈)becomes

which arises in different models,for example,to get a standing wave,that is,a solution of the form Ψ(x,t)=exp(−iEt/∈)u(x)of the following nonlinear Schrödinger equation

where f(t)=|t|s−2t,N ＞ 2,and 2＜ s＜ 2∗=,and it will led to the study of(1.2).Many studies about the existence and concentration of positive solutions for problem(1.2)appeared in the past decade;see[1,4,16]and the references therein.

Recently,the following Kirchhofftype equation

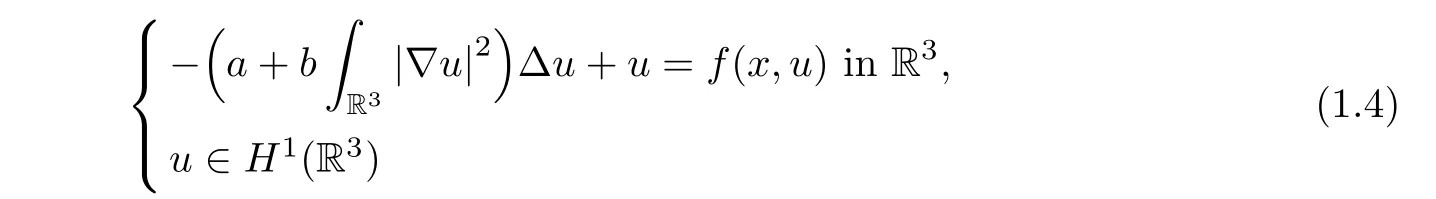
has been studied extensively by many researchers,where f∈C(R3×R,R),and a,b＞0 are constants.

X.He and W.Zou in[7]studied(1.4)under the conditions that f(x,u):=f(u)∈C1(R+,R+)satisfies the Ambrosetti-Rabinowitz condition((AR)condition in short):

Similarly,J.Wang et al[15],Y.He,G.Li,and S.Peng[9],and G.Li and H.Ye[11]used the same arguments as in[7]to prove the existence of a positive ground state solution for(1.4)when f(x,u):=λf(u)+|u|4u,which exhibits a critical growth,wheref(u)u≥0,f(u)/u3is strictly increasing for u＞0,and |f(u)|≤C(1+|u|q)for some 3＜q＜5,that is,f(x,u)∼ λ|u|p−2u+|u|4u(4＜ p＜ 6).

For the case f(x,u)=|u|p−2u(3＜ p≤ 4),G.Li and H.Ye[10]used the constrained minimization on a new manifold,which is obtained by combining the Nehari manifold and the corresponding Pohozaev’s identity,to get a positive ground state solution to(1.4).

Recently,Y.He and G.Li in[8]studied the following Kirchhofftype equation with critical nonlinearity:

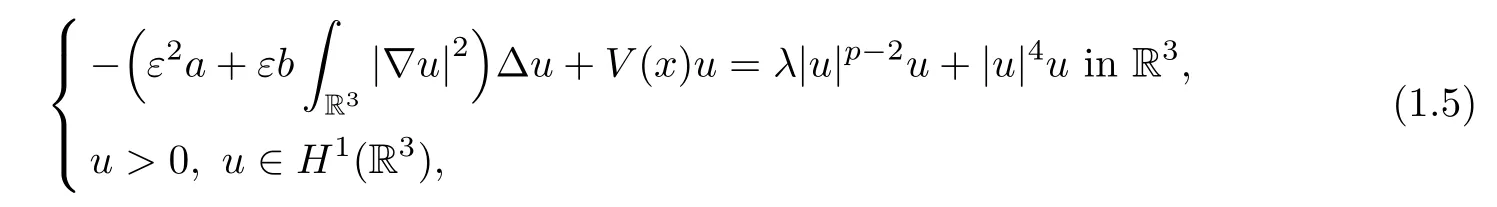
where ε is a small positive parameter,a,b＞ 0,λ ＞ 0,and 2＜ p≤ 4.The potential V satisfies(V3)V∈C(R3,R)and

(V4)there is a bounded domain Λ such that

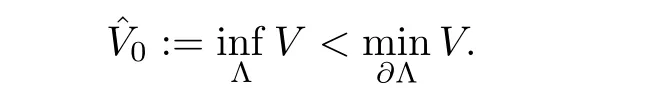
They constructed a family of positive solutions uε∈ H1(R3)which concentrates around a local minimum of V as ε→ 0.

M.del Pino and P.Felmer in[4]studied(1.2)with the conditions on V replaced by(V3)and(V4).They proved that(1.2)possesses a positive bound state solution for ε＞ 0 small which concentrates around the local minima of V in Λ as ε→ 0.

In[6],G.Figueiredo,N.Ikoma,and J.Junior obtained the existence of positive solutions of the following equation

concentrating around a local minima of V under the conditions(V3),(V4),and the following conditions on f and M:

(F1)f∈C(R,R),f(s)=0 if s≤0;

(F2)−∞＜

(F3)when N ≥ 3,f(s)/s(N+2)/(N−2)→ 0 as s→ ∞ and when N=2,f(s)/eαs2→ 0 as s→∞for any α＞0;

(F4)there exists an s0＞0 such thatwhere F(s):=f(t)dt when N≥2,and when N=1,−and there exists a＞0 such that M(t)≥＞0 for any t≥2;then,there holds→0 as t→∞;

G.Figueiredo and J.Santos in[5]studied the multiplicity and concentration behavior of positive solutions of the following elliptic problem

where∈is a small positive parameter,the potential V satisfies(V1)and(V2),and the function M:[0,∞)→R+satisfies

(M1)M∈C()andM(t)≥ m0＞ 0,where m0＞ 0 is a constant;

(M2)the function t→M(t)is increasing on[0,+∞);

(M3)for all t1≥t2＞0,

and f satisfies

(F5)

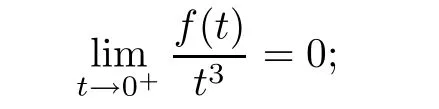
(F6)there is a q∈(4,6)such that

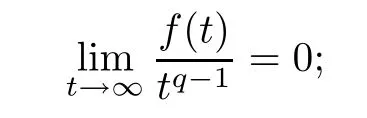
(F7)there is a θ∈(4,6)such that

(F8)the application

is nondecreasing in(0,∞).

Motivated by the results in[5],we study the existence,multiplicity,and concentration behavior of positive solutions of the problem(Q∈)by using the variational method and the penalization method.

Before stating our main result,we make the following hypotheses:

(f1)f ∈ C(R,R)and there exist q,with p＜ q＜ p∗,a1＞ 0 such that|f(t)|≤ a1(1+|t|q−1)for all t＞0;

(f2)there exists θ＞ 2p such thatfor all t＞ 0;

(f3)f(t)=o(|t|p−1)as t→ 0;

(f4)the functionis increasing for t＞ 0.

We define

with the norm

It is easy to see that(E,‖ ·‖E)is a real Banach space.

We call u ∈ E a weak solution to(Q∈)if for any ϕ ∈ E,it holds that

For I∈C1(E,R),we say that(un)⊂E is a Palais-Smale(PS)sequence at level c(henceforth denoted(PS)c)for I if(un)satisfies

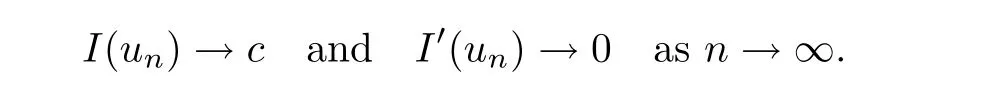
Moreover,I satisfies the(PS)ccondition if any(PS)csequence possesses a convergent subsequence.

We recall that,if A is a closed set of a topological space of X,CatX(A)is the Ljusternik-Schnirelmann category of A in X,namely,the least number of closed and contractible sets in X which cover A.

Our main result is as follows:

Theorem 1.1Suppose that the function M satisfies(M1)–(M3),the potential V satisfies(V1)–(V2),and the function f satisfies(f1)–(f4).Then,for any δ＞ 0,there exists a ∈δ＞ 0 such that,for any ∈∈ (0,∈δ),the problem(Q∈)has at least CatΠδ(Π)positive solutions.Moreover,if u∈denotes one of these positive solutions and η∈∈ RNits global maximum,then

Remark 1.2Our main result for the problem(Q∈)when p=2 includes the main result of[5]as a special case.A typical example of function f satisfying the conditions(f1)–(f4)is given bywith λi≥ 0 not all null and 2p ＜ qi＜ p∗for all i∈ {1,2,···,k}.Any function of the formsatisfies the hypotheses(M1)–(M3)for all i∈ {1,2,···,k},where m0＞ 0,b＞ 0,bi≥ 0,and γi∈ (0,1).

The proof of Theorem 1.1 is based on the frame work used in[5]which uses the Lusternik-Schnirelmann theory and abstract minimax theorems(see[14,17]).The main difficulties are the appearance of the non-local term and the lack of compactness because of the unboundedness of the domain RN.Moreover,as f is only continuous,we cannot use standard arguments on the Nehari manifold.As we will see later,the competing effect of the nonlocal term with the nonlinearity f(u)and the lack of compactness of the Sobolev’s embedding prevent us from using the variational methods in a standard way.

Now,we outline the sketch of the proof of our main result.The problem(Q∈)is equivalent to the following problem

by using the change of variable v(x)=u(∈x).The corresponding energy functional associated with problem()is defined by

∈

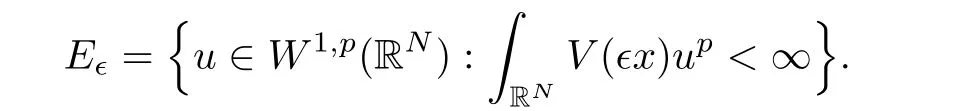
The norm of u ∈ E∈is defined asand E∈is a Banach space under the norm ‖ ·‖∈given above.

In order to overcome the obstacle caused by the non-compactness because of the unboundness of the domain RN,following[4],we will modify the nonlinearity in a special way and to work with a auxiliary problem.

Let δ＞ 0 and the related bounded domain Λ be given as in(V2)and letwhere m0was given in(M1),and a＞0 verifyingwhere V0＞0 was given in(V1).We consider the following auxiliary problem

where

with

Here,χΛdenotes the characteristic function of the set Λ.

It is easy to see that under the assumptions(f1)–(f4),g(x,t)is a Caratheodory function satisfying the following assumptions:

(g1)g∈(x,t)=o(|t|p−1)as t→ 0 uniformly in x ∈ RN;

(g2)g(x,t)≤f(t)for all x∈RN,t＞0;

(g3)0 ＜ θG∈(x,t)≤ g∈(x,t)t,∀(x,t)∈ Λ∈×(0,∞),where θ is given in(f2);

(g4)

(g5)for each x∈ Λ,the application t→is increasing in(0,∞),and for each x ∈ RNΛ,the application t→is increasing in(0,a).

The energy functional I∈:E∈→ R associated with(Q∈,g)is given by

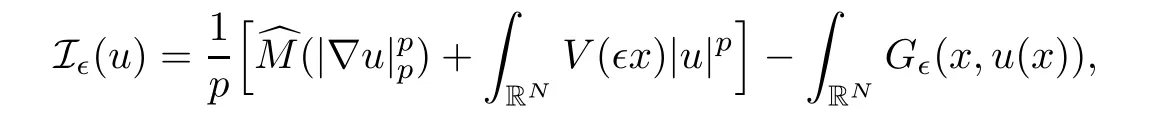
Using variational method,we can prove that the auxiliary functional I∈satisfies the Palais-Smale condition,and the auxiliary problem(Q∈,g)has a positive ground state solution for all∈＞0.

Because we are interested in giving a multiplicity result for the auxiliary problem(Q∈,g),we need to study the limit problem associated to(),namely,the following problem

with the energy functional

This functional is well defined on the spacewith the norm

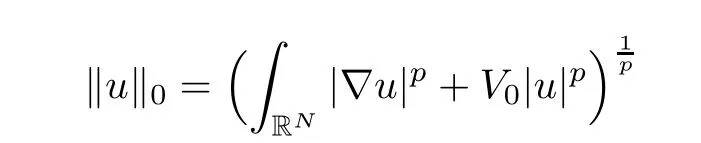
for u0∈E0.Next,using the technique due to V.Benci and G.Cerami[2],we establish a relationship between the category of the set Π and the number of solutions for the auxiliary problem,and we will show that(Q∈,g)has multiple positive solutions by using Lusternik-Schnirelmann theory.Finally,we use the Moser iteration technique in[13]to prove that the solutions for the auxiliary problem(Q∈,g)are indeed solutions for the original problem.

We note that the function f in this article is only a continuous function,then we cannot apply standard arguments by using the Nehari manifold.We overcome this difficulty by the methods given in[14].

Throughout this article,we use standard notations.For simplicity,we writeRΩh to mean the Lebesgue integral of h(x)over a Lebesgue measurable set Ω⊂RN.For a Lebesgue measurable set A,we denote the Lebesgue measure of A by|A|.Lp=Lp(RN)(1＜p≤∞)is the usual Lebesgue space with the standard norm|·|p.We use“→ ”and“⇀ ”to denote the strong and weak convergence in the related function spaces,respectively.C and Ciwill denote positive constants unless specified.BR(x):={y ∈ RNy − x|＜ R,x ∈ RN}. 〈·,·〉denote the dual pair for any Banach space and its dual space.

2 The Auxiliary Problem

By using the change of variable v(x)=u(∈x),we see that problem(Q∈)is equivalent to the following problem

In order to find positive solutions to(),without loss of generality,we shall assume that f(s)=0 for all s≤ 0.The corresponding energy functional associated with problem()is defined by

∈given by

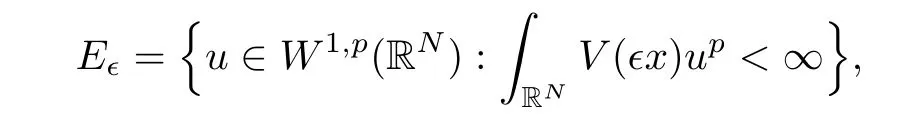
in which the norm of u∈E∈is given by

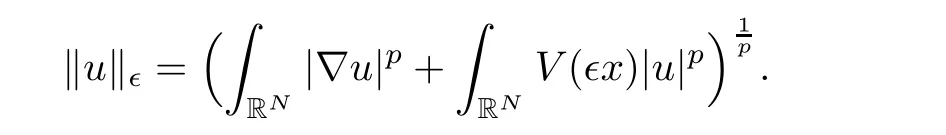
We see that J∈∈ C1(E∈,R)and

From now on,we will denote by E0the space E∈with∈=0.We know that E∈is continuously embedded in Lν(RN)for ν ∈ [p,p∗];moreover,E∈is compactly embedded in Lν(A)for ν ∈[p,p∗)for any bounded measurable set A ⊂ RN.

In order to overcome the lack of compactness of the problem(eQ∈),we shall adapt the penalization method introduced by del Pino and Felmer in[4].

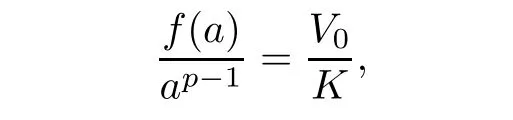
where V0＞0 was given as in(V1).Using these numbers,we set the functions

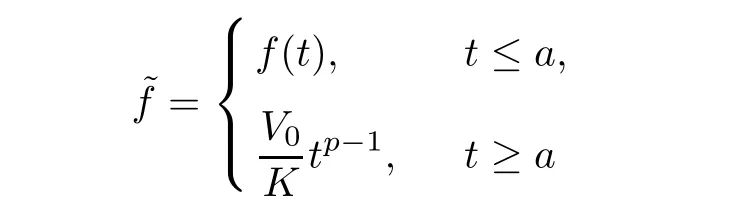
and

where Λ was given as in(V2)for related fixed δ＞ 0,and χΛdenotes the characteristic function of the set Λ.

Using the above functions,we will study the existence of positive solution for the following auxiliary proble

where

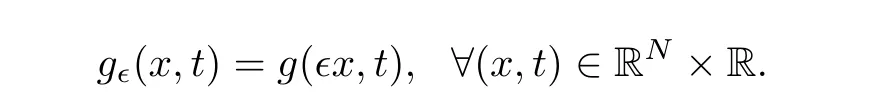
Here,we recall that if u∈∈ E is a solution to prpblem(Q∈,g)with

where Λ∈= Λ/∈,then,u∈(x)is a solution of problem().

Associated with(Q∈,g),we have the energy functional I∈:E → R given by

where

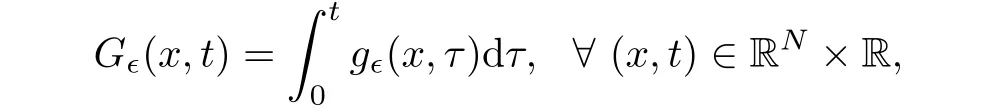
which is well defined on the space E∈and I∈∈ C1(E∈,R).Also,

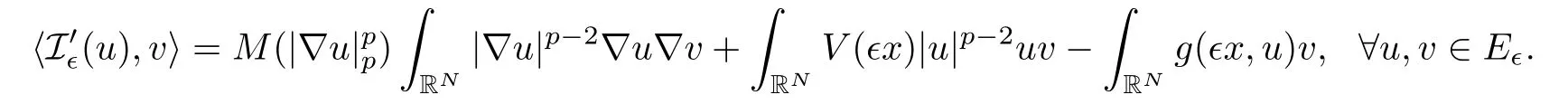
Using the definition of g,it follows that

(g1)g∈(x,t)=o(|t|p−1)as t→ 0 uniformly in x ∈ RN;

(g2)g(x,t)≤f(t)for all x∈RN,t＞0;

(g3)0 ＜ θG∈(x,t)≤ g∈(x,t)t,∀(x,t)∈ Λ∈×(0,∞),where θ is given in(f2);

(g4)0 ≤ 2pG∈(x,t)≤ g∈(x,t)t≤,∀(x,t)∈ (Λ∈)c× (0,∞);

(g5)for each x∈ Λ,the application t→is increasing in(0,∞)and for each x ∈ RNΛ,the application t→is increasing in(0,a).

Lemma 2.1The functional I∈satisfies the following conditions:

(i)There are α0＞ 0,ρ0＞ 0 such that

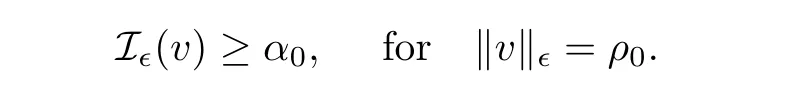
(ii)There is an e∈ E∈with ‖v‖∈＞ ρ0and I∈(e)＜ 0.

Proof(i)From(g1)and(g2),for every∈＞0,we have

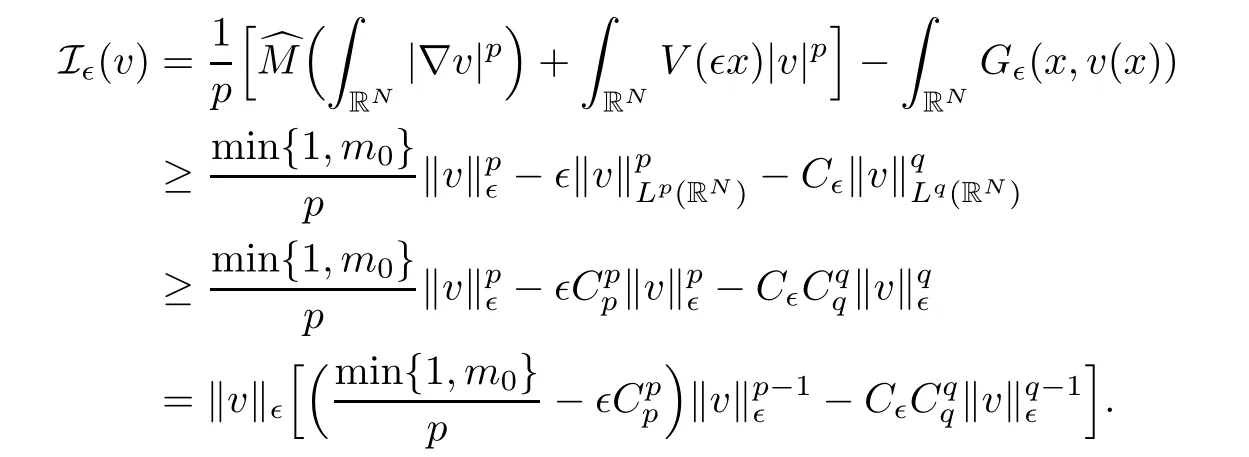
Taking∈=min{1,m0}/2pCppand setting

we see that there exists an ρ0＞ 0 such thatas q ＞ p ＞ 1 by(f1),we obtain I∈(v)≥ α0= ρ0η(ρ0)＞ 0 for all v ∈ E∈,with ‖v‖∈= ρ0.

(ii)Fix u ∈ E∈with suppu ⊂ Λ∈,and ‖u‖∈=1.By assumption(M3),we see that there is a γ1＞ 0 such that M(t)≤ γ1(1+t)for all t≥ 0.

Then,for t＞0,we have

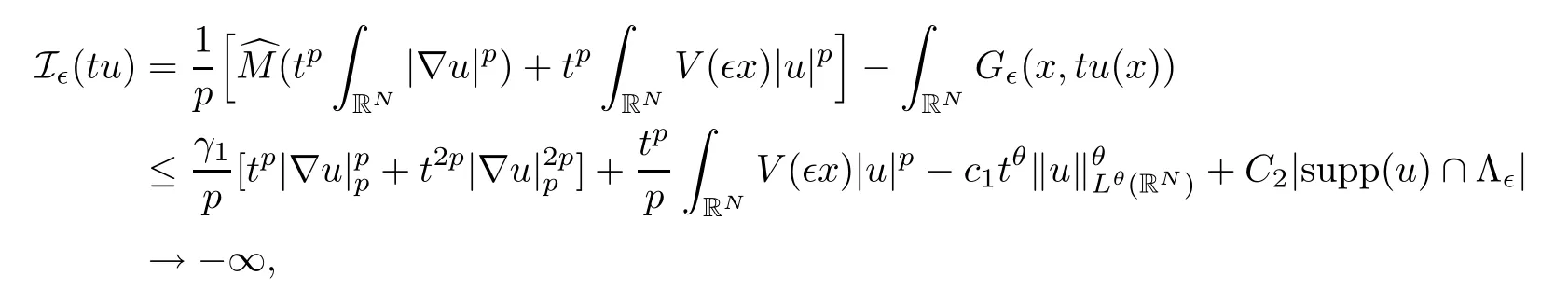
because θ＞ 2p＞ p＞ 1 by(f2).The Lemma 2.1(ii)is then proved by taking v=t0u,with t0＞0 large enough.

The main feature of the auxiliary functional is that it satisfies the Palais-Smale condition as we can see from the next result.

Proposition 2.2The functional I∈verifies the(PS)ccondition in E∈for any c＞0.

Proof(1)Assume that{un}is a(PS)csequence for I∈,then,

By using the hypothesis(M3),we deduce thatfor all t≥0.By(g3)and(g4),we obtain

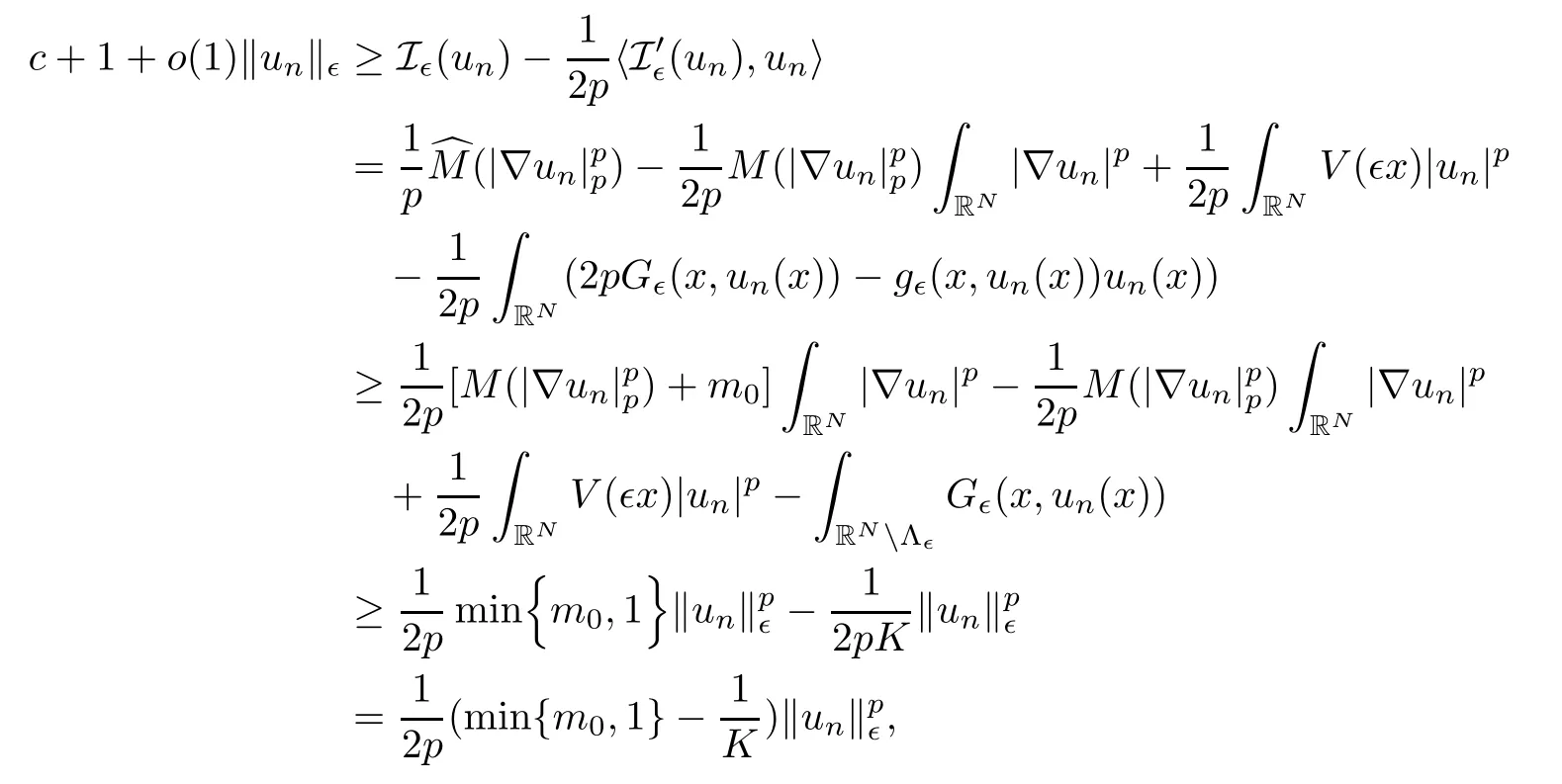
therefore,{un}is bounded in E∈.Passing to a subsequence,for some u ∈ E∈,we obtain

Next,we will prove that{un}has a convergent subsequence in E∈.Firstly,we give two claims,

Claim 1For all R＞0,

Indeed,we assume that‖un‖∈→ t0as n → ∞,we have‖u‖∈≤ t0.Take ηρ∈ C∞(RN)such that

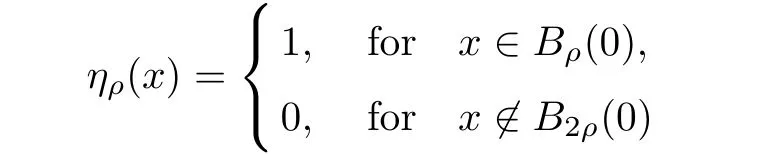
For each R ＞ 0 fixed,denoting a(ξ,η)=(|ξ|p−2ξ− |η|p−2η,ξ− η),it is well known that a(ξ,η)＞ 0 for any p ＞ 1 and ξ,η ∈ RNwith ξ/= η.Choosing ρ ＞ R,we obtain

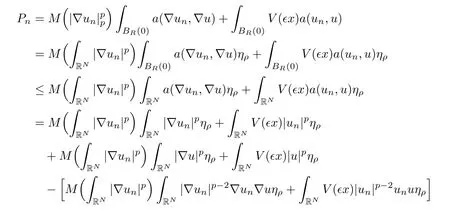
Setting

we have

Observe that

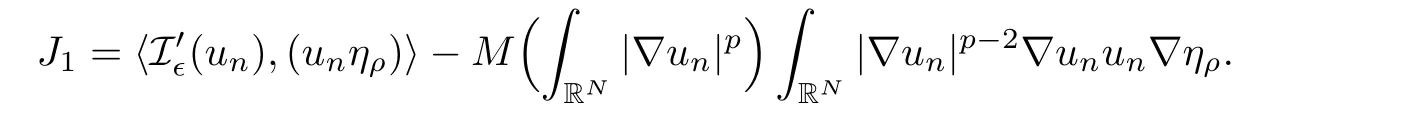
As{unηρ}is bounded in E∈,we have〈I′∈(un),(unηρ)〉=on(1).Moreover,from a straight forward computation,

thus,

On the other hand,from the weak convergence,

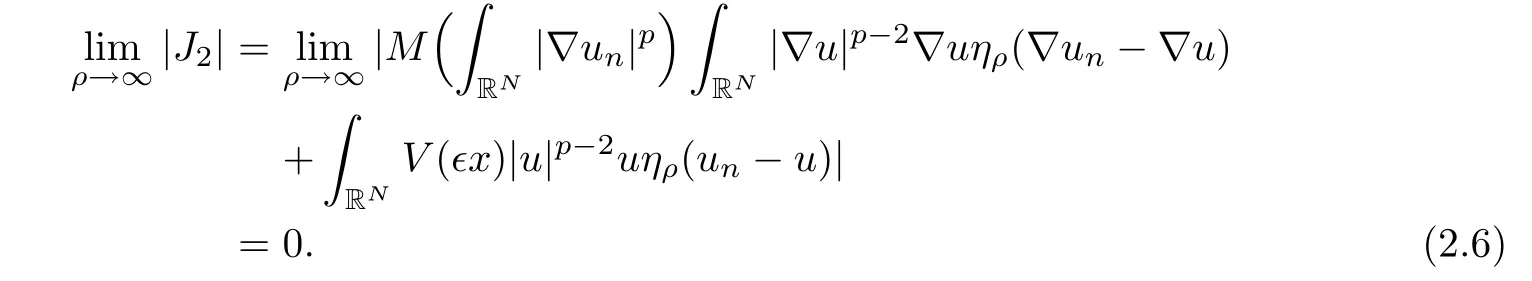
We see that

We conclude that

From(2.3),(2.5)–(2.8),we obtain

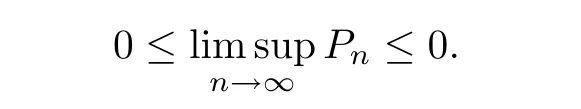
Hence,we obtain

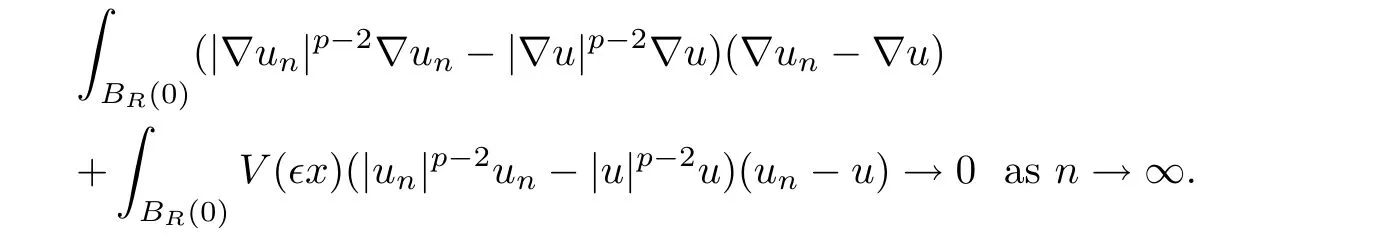
By Lemma 2.1 of[3],for p ≥ 2 and ξ,η ∈ RN,

for 1 ＜ p ＜ 2 and ξ,η ∈ RN,

here,d1,d2,d3,and d4are some constants.

Using the above inequalities,for 1＜p＜2,we know that

For p≥2,

and consequently,

Claim 2For each ξ＞ 0,there is an R=R(ξ)＞ 0 such that

For R ＞0,let ηR∈C∞(RN)be such that

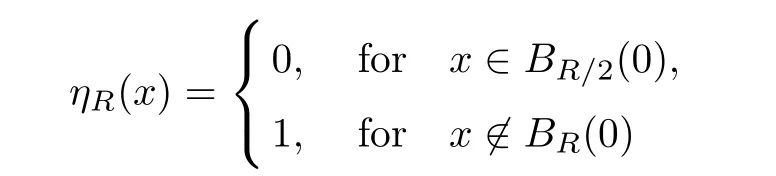
with 0 ≤ ηR(x)≤ 1,|∇ηR|≤,and C is a constant independent on R.Because{ηRun}is bounded in E∈,it follows fromthat

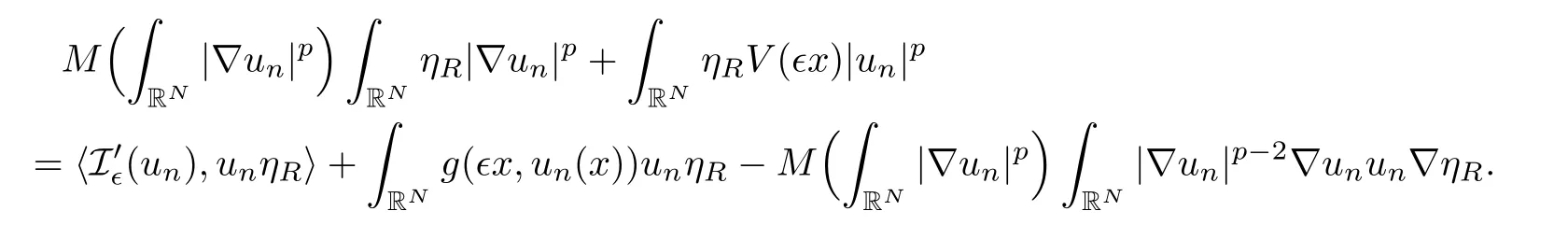
Therefore, fixing R ＞ 0 such that Λ∈⊂ BR2(0)and by using(M1)and(g3),we have

Thus,

By using Cauchy-Schwarz and Hölder’s inequality,we have

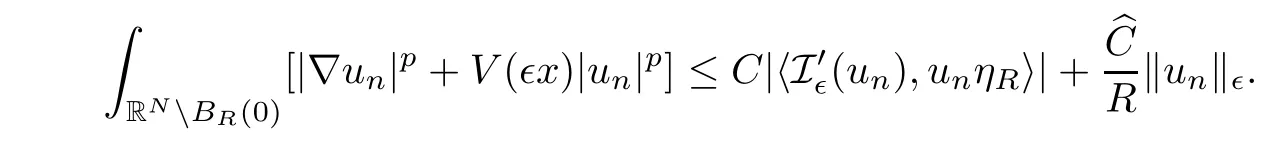
As{un}and{unηR}are bounded in E∈,we obtain

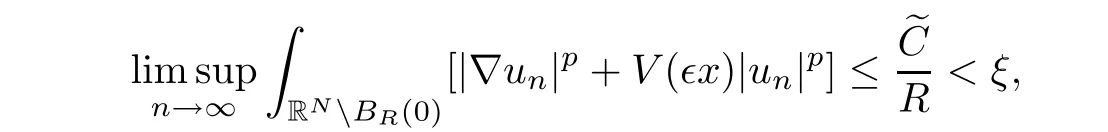
Therefore,for each ξ＞ 0,there is an R=R(ξ)＞ 0 such that

hence,‖un‖∈→ ‖u‖∈,and un→ u in E∈.

Theorem 2.3Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.Then,the auxiliary problem(Q∈,g)has a positive ground state solution for all∈＞ 0.

ProofThis result follows from Lemma 2.1,Proposition 2.2,and the maximum principle.

Next,we introduce some tools needed for the multiplicity result of the auxiliary problem(Q∈,g).

We denote by N∈the associated Nehari manifold of I∈given by

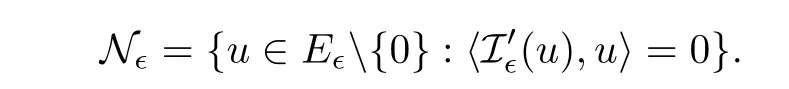
Set Γu+={x∈RN|u+(x)/=0},letbe the open subset of E∈given by

The idea of the proof of the next two results comes from[14](See also[5]).

Lemma 2.4Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.Then,we have the following results:

(A1)For each u∈and by hu(t)=I∈(tu),there exists a unique tu＞0 such that＞0 in(0,tu)and＜ 0 in(tu,∞).

(A2)There is a τ＞0 independent on u such that tu＞ τ for all u∈Moreover,for each compact set W⊂,there is a CW＞0 such that tu≤CWfor all u∈W.

(A3)The mapgiven byis continuous andis a homeomorphism betweenand N∈.Moreover,

(A4)If there is a sequence(un)⊂such that dist(un,)→0,then,‖r∈(un)‖∈→ ∞and I∈(r∈(un))→ ∞ as n → ∞ for each ∈＞ 0.

ProofIt is clear that,by Lemma 2.1,hu(0)=0,hu(t)＞0 for t＞0 small,and hu(t)＜0 for t＞ 0 large.Thus,there is a global maximum point tu＞ 0 of husuch that=0,that is,tuu∈ N∈.We claim that there is a unique tu＞ 0 such that=0.Indeed,suppose that there exist t1＞t2＞0 withThen,for i=1,2,

Therefore,

By using(M3)and the definition of g,we obtain

So,

As u/=0,which is absurd in view of min{m0,1}≤＜min{m0,1}.Thus,(A1)is proved.

which implies that tu≥τ for some τ＞0.If W⊂is compact,then argue by contradiction that there is a sequence{un}⊂W such that tun→∞.As W is compact,there is a u∈W with un→ u in E∈.By the process of the proof of Lemma 2.1,we know that I∈(tunun)→ −∞.Note that if v∈ N∈,then,by(M3),(g3),and(g4),we obtain

Because{tunun}⊂ N∈,which contradicts to the fact that{tunun}⊂ N∈and I∈(tunun)→−∞.This proves(A2).

So,by(M1),we have

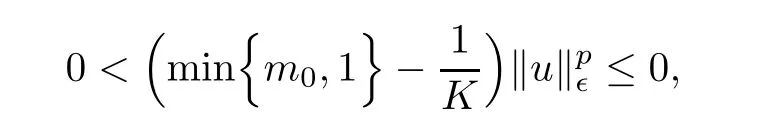
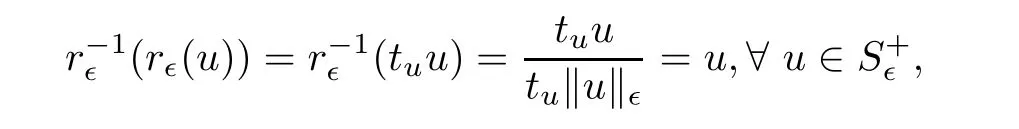
we conclude that r∈is a bijection betweenand N∈.

Letting n→∞,we have

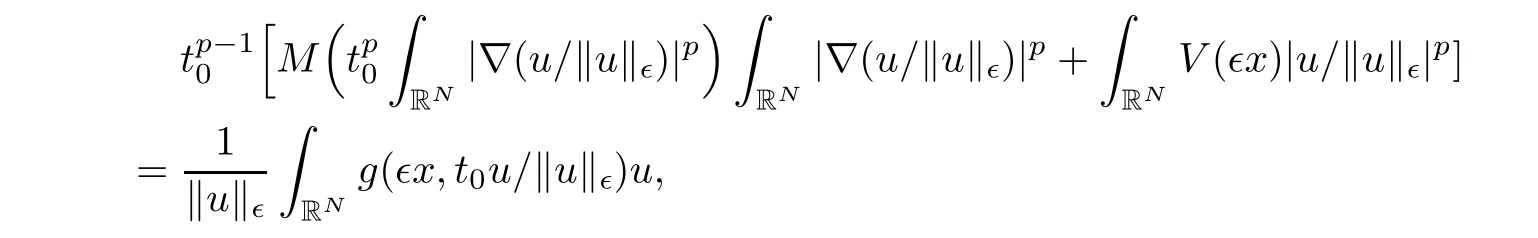
It follows from(f1),(g3),and(g4)that

for each t＞0.Thus,

By using the definition of r∈,we get

As t＞0 is arbitrary,we have

We conclude from(M3)that

for each n ∈ N,so,‖r∈(un)‖∈→ ∞ as n → ∞.The Lemma is proved.

Now,we define the applications

The next proposition can be found in[[14],Corollary 2.3],and we omit the proof of it.

Proposition 2.5Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.Then,the following properties are obtained:(a)and

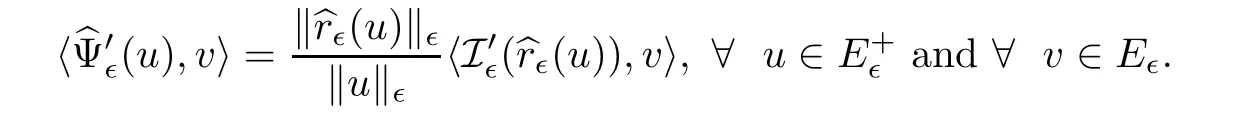
(c)If{un}is a(PS)csequence of Ψ∈,then,{r∈(un)}is a(PS)csequence for I∈.If{un} ⊂ N∈is a bounded(PS)csequence of I∈,then,{(un)}is a(PS)csequence for Ψ∈.

(d)u is a critical point of Ψ∈if and only if r∈(u)is a nontrivial critical point of I∈.Moreover,the corresponding critical values Ψ∈and I∈coincide,and

Remark 2.6As in[14],we have the following minimax characterization of the in fimum of I∈over N∈,

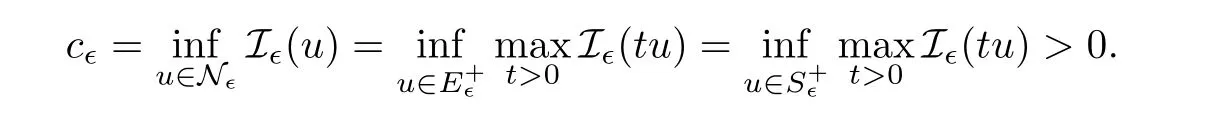
Corollary 2.7([5],Corollary 2.1) The functional Ψ∈given in Proposition 2.5 satisfies the(PS)ccondition on.

3 Multiplicity of Solutions of Auxiliary Problem

3.1 The autonomous problem

In this section,we prove a multiplicity result for problem(Q∈,g).We first consider the associated limit problem of(),which is given as

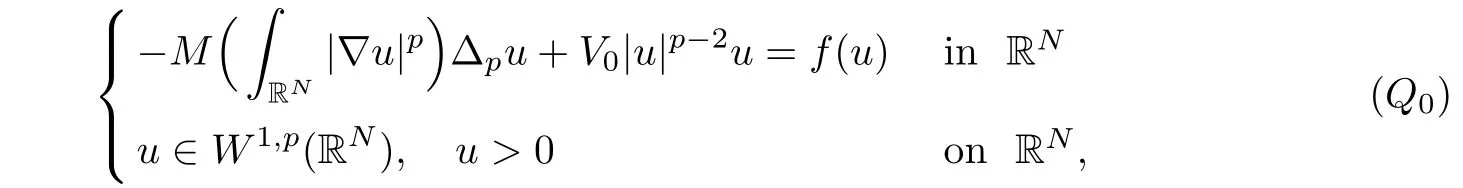
with the corresponding energy functional

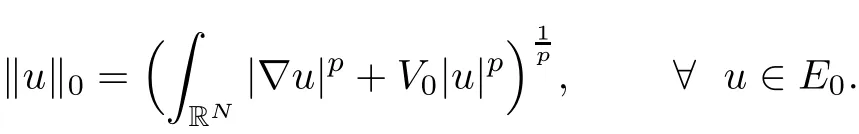
We denote by N0the associated Nehari manifold of J0given by

Lemma 3.1Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.Then,we obtain the following results:

(A1)For each u∈and by gu(t)=J0(tu),there is a unique tu＞0 such that＞0 in(0,tu)and＜0 in(tu,∞).

(A2)There is a τ＞0 independent on u such that tu≥ τ for all u∈.Moreover,for each compact set W⊂there is a CW＞0 such that tu≤CWfor all u∈W.

(A3)The map:→N0given by=tuu is continuous,and r=is a homeomor

(A4)If there is a sequence{un} ⊂such that dist(un,)→ 0,then,‖r(un)‖0→ ∞ and J0(r(un))→∞as n→∞for each∈＞0.

ProofThe proof of Lemma 3.1 is similar to that of Lemma 2.4.

We set the applications

Proposition 3.2Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.So,we have the following properties:and

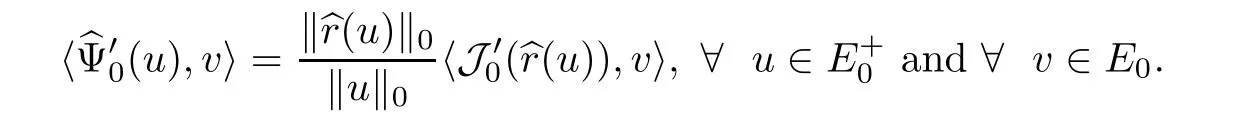
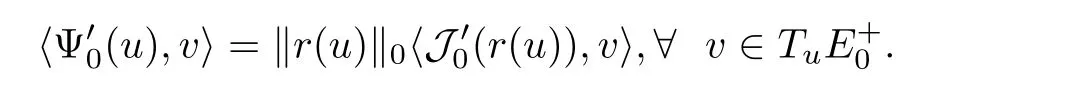
(c)If{un}is a(PS)csequence of Ψ0,then,{r(un)}is a(PS)csequence of J0.If{un} ⊂ N0is a bounded(PS)csequence of J0,then,{r−1(un)}is a(PS)csequence of Ψ0.

(d)u is a critical point of Ψ0if and only if r(u)is a nontrivial critical point of J0.Moreover,corresponding critical values coincide and

ProofThe proof of Proposition 3.2 is similar to that of Proposition 2.5.

Remark 3.3Similar to Remark 2.6,we have

Lemma 3.4Assume that{un}⊂E0is a(PS)csequence for J0satisfying un⇀0 in E0.Then,one and only one of the following alternatives holds,

(a)un→0 in E0,or

(b)there exist constants R,β＞0 and sequence{yn}⊂RNsuch that

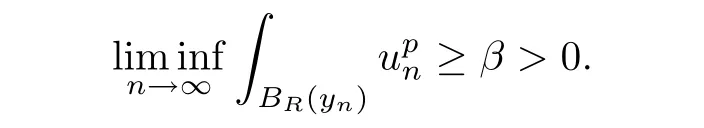
ProofSuppose that case(b)is flase,we would have

for all R ＞ 0.Since{un}is bounded in E0,again using Lion’s vanishing Lemma(See[12],Lemma 1.1),we have

By(M1),(f1),and(f3),we obtain

therefore,un→ 0 in E0,which contradicts our assumption I∈n(un)→ c0.Thus,(a)holds. □

Theorem 3.5Assume that{un}⊂E0is a(PS)csequence for J0,where c0is given in Remark 3.3.Then,problem(Q0)has a positive ground state solution.

ProofArguing as in the proof of Proposition 2.2,we see that{un}is bounded in E0.Now,up to a subsequence,for some u∈E0,we have

By Lemma 3.4 and c0＞ 0,we know that u/=0 in E∈.There exists a t0＞ 0 such that

Step 1We claim∇un→∇u a.e.x∈RN.

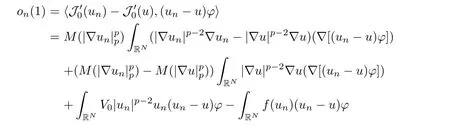
By(3.1)–(3.3)and{un}being bounded in E0,we see easily that

as n→∞.

hence,by(M1),we have

For 1＜p≤2,from(2.10),we know that

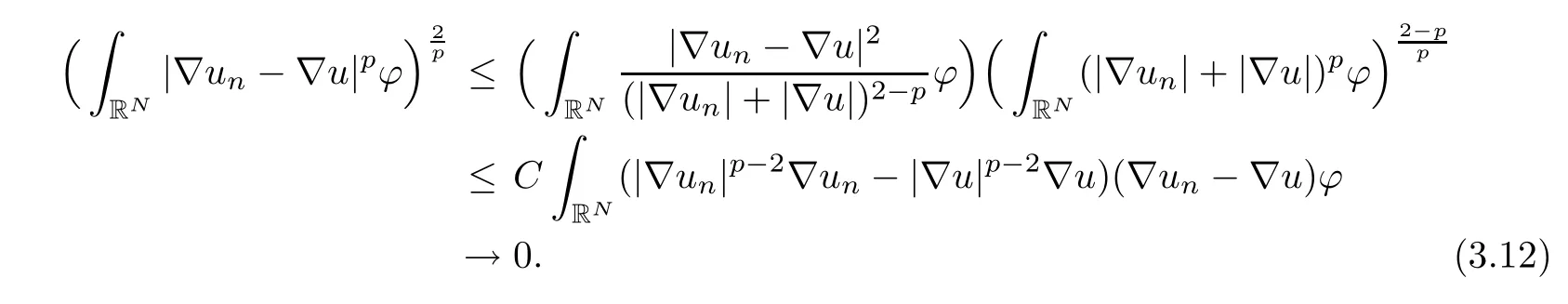
For p≥2,from(2.9),we obtain

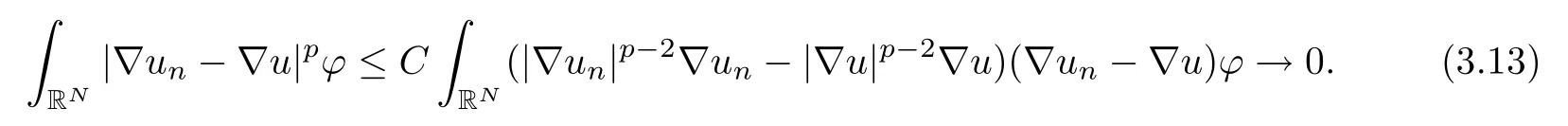
The above limits(3.12)and(3.13)imply that for some subsequence of{un},we have

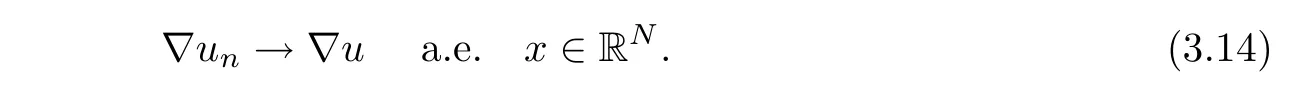
So,from(3.14),we conclude that

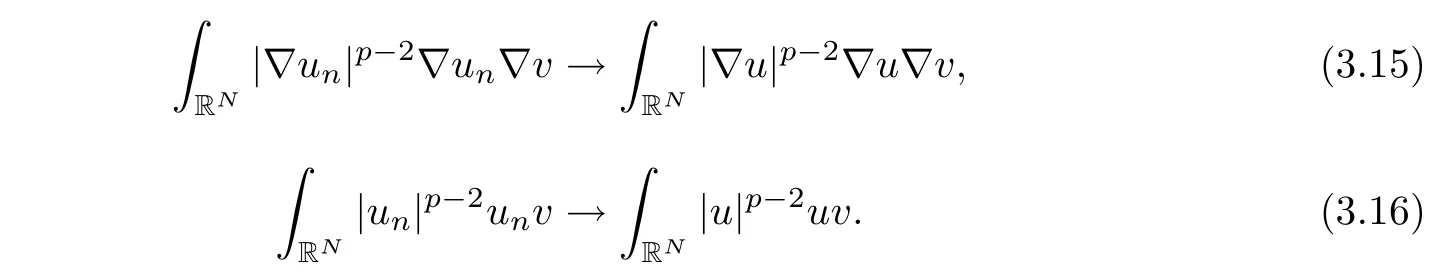
On the other hand,by Vitali’s theorem,it results that

Step 2We claim thatwhere t0is given in(3.4).

Now,by(3.1)and(3.3),we have

and from(M2),it follows thatJust suppose thatwe obtain

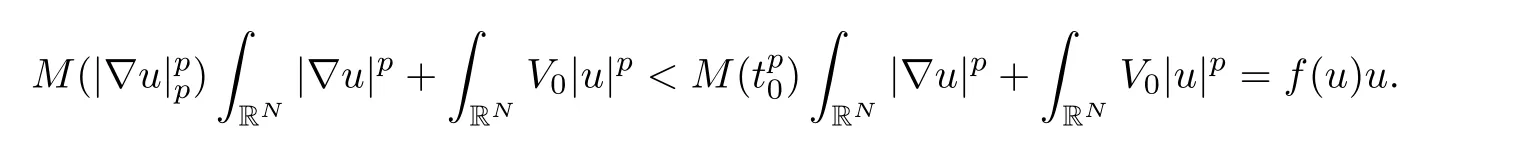
This inequality implies thattherefore,there exists a∈(0,1)such thatCombining this information with the characterization c0,we derive

On the other hand,from(M3),we getby Fatou’s Lemma,we obtain

Lemma 3.6([5],Lemma 3.3) Assume that{un}is a sequence in W1,p(RN)such that,as n→∞,J0(un)→c0and{un}⊂N0.Then,{un}has a convergent subsequence in W1,p(RN).

ProofThis result can be proven by using,with suitable modifications,the same arguments of[5].

3.2 Some technical results

In this subsection,we will establish the relation between the topology of the set Π and the number of positive solutions of(Q∈,g).We choose δ＞0 such that Πδ⊂ Λ.Let η ∈([0,∞))be such that 0≤η(t)≤ 1 with

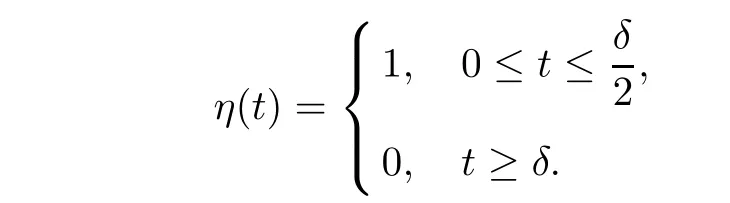
We denote w to be a positive ground state solution of the problem(Q0)attained by Theorem 3.5 such that J0(w)=c0.For each y∈Π={x∈Λ:V(x)=V0},we define

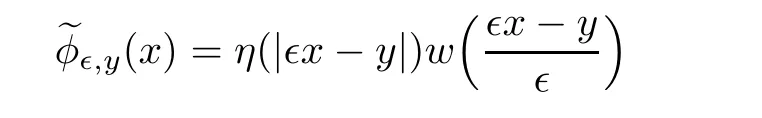
with t∈＞ 0 satisfying

Let φ∈:Π →N∈be such that

Lemma 3.7The function φ∈satisfies

ProofAssume the contrary that the lemma does not hold.We suppose that there exist δ0＞0 and a sequence{yn}⊂Π such that

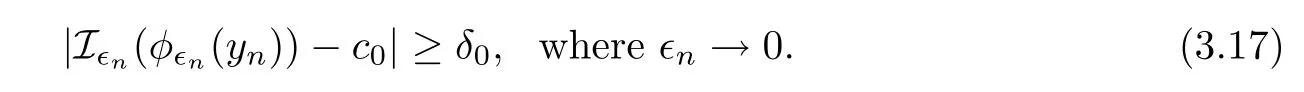
By using the change of variableand the definition of φ∈n(yn),we have

Since φ∈n(yn) ∈ N∈nand g=f in Λ,we get

and

Set

By the Lebesgue’s theorem,as n → ∞,we obtain

and

Now,we claim that,up to a subsequence,t∈n→ 1 as n → ∞.Indeed,in view of(3.19),we have

From continuity of w,there is asuch thatSo,from(f4),we get

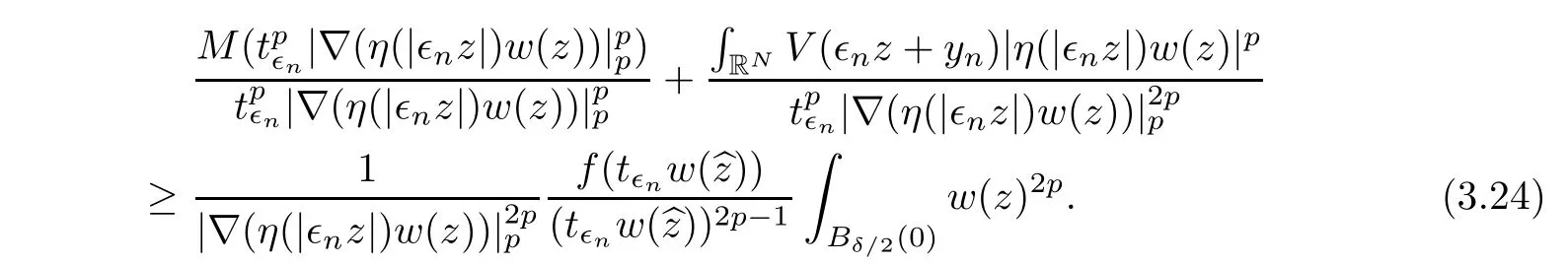
Assume the contrary that there is a subsequence{t∈n}with t∈n→ ∞.Thus,taking n → ∞in(3.24),by(M3)and(f3),we have the fact that the downside converges to in finity and the upside is bounded,which leads to a contradiction.Thus,{t∈n}is bounded,up to a subsequence,we have t∈n→t0≥0.From(3.19),(3.21),(M1),and(f4),we have t0＞0.Thus,as n→∞in(3.19),we have

We get t0=1 from w∈N0.So,taking n→∞in(3.20)and combining(3.21)with(3.22),we get

which contradicts to(3.17).

Proposition 3.8Assume that{un}is a sequence in W1,p(RN)such that,as n→∞,

and

with∈n→0.Then,there existssuch that the sequencehas a convergent subsequence in W1,p(RN).Moreover,up to a subsequence,forand some y∈Π,we have yn→y.

ProofDirect calculations shows that{un}is bounded in W1,p(RN),then we can argue as the proof of Lemma 3.4 to obtain a sequence()⊂RNand positive constants R and α such that

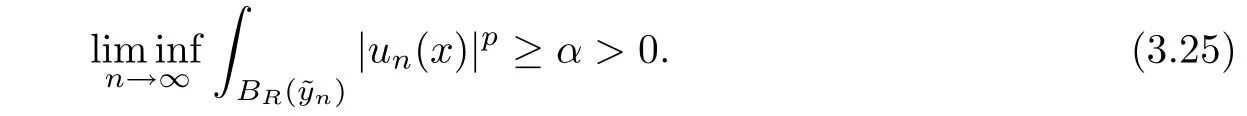
Let tn＞0 be such that(See Lemma 3.1(A1)).We have

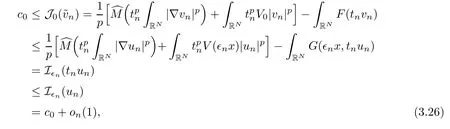
which implies that

Now,we are going to prove that→y∈M.First,we will prove that{yn}is bounded,where yn=.Indeed,argue by contradiction that there exists a subsequence{yn}with|yn|→∞.Choose R＞0 such that Λ⊂BR(0).Then,for n large enough,we have|yn|≥2R,and for each z∈(0),we have

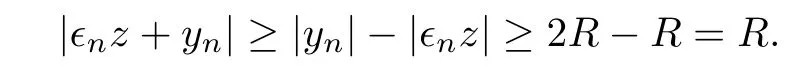
Hence,using vn→ v in E0,the above expression,the definition of g,and Lebesgue’s theorem,we obtain

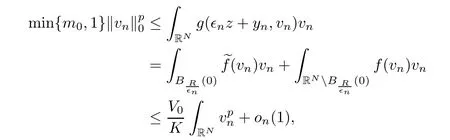
and therefore,

which is a contradiction.Hence,{yn}is bounded and yn→ y in RN.If y/∈ Λ,we can proceed as above to deduce that‖vn‖0≤ on(1).

Next,we prove that y∈Π.Arguing by contradiction again,we assume that V0＜V(y).Consequently,from→in E0,Fatou’s Lemma,and the invariance of RNby translations,we have

which does not make sense and completes the proof.

Remark 3.9Proposition 3.8 is very important to show that the solution of the auxiliary problem are actually solution of the original problem,and it makes us possible to study the concentration behavior of the solutions.

Define

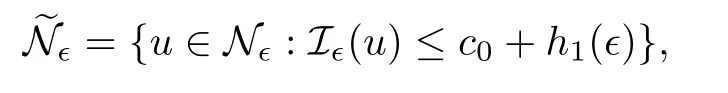
where h1:R+→ R+is a function such that lim∈→0h1(∈)=0.We can conclude from Lemma 3.7 that h1(∈)=|I∈(φ∈(y))−c0|is such that h1(∈)→ 0 as∈→ 0+.By the definition of h1,we know that,for any y∈Π andfor∈＞0 small.

Let ρ ＞ 0 be such that Πδ⊂ Bρ(0),and consider the map χ :RN→ RNdefined by

We define the barycenter map β∈:N∈→ RNby

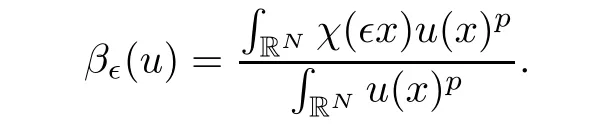
By the definition of χ and Lebesgue’s theorem,we have

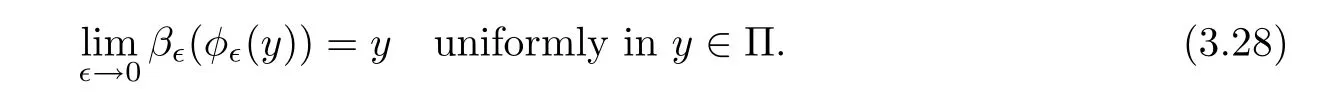
Lemma 3.10For any δ＞ 0 and Πδ={x ∈ RN:dist(x,Π)≤ δ},we have

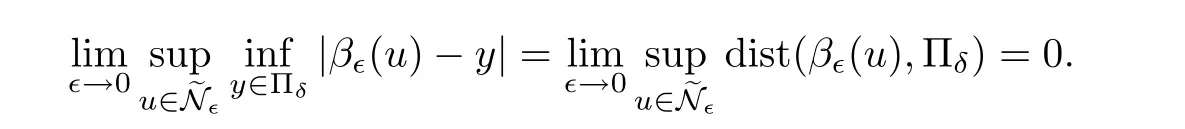
ProofThe proof of this lemma follows from well-known argument and can be found in([5],Lemma 5.5).

3.3 Multiplicity of solutions for(Q∈,g)

In this section,we present a relation between the topology of Π and the number of solutions of the auxiliary problem(Q∈,g).Asis not a complete metric space,the method of[1]can not be applied directly,but we can use the result in[14]to fulfill our task.

Lemma 3.11([14],Theorem 27)If there exist c≥c∈and a compact set K⊂suchfor some k∈N,wherethencontains at least k critical points of Ψ∈.

Theorem 3.12Suppose that the conditions(M1)–(M3),(V1)–(V2),and(f1)–(f4)are satisfied.Then,for any δ＞0,there exists a＞0 such that the auxiliary problem(Q∈,g)has at least CatΠδ(Π)positive solutions for any∈∈(0,).

ProofFor each∈＞0,we define the function ζ∈:Π →by

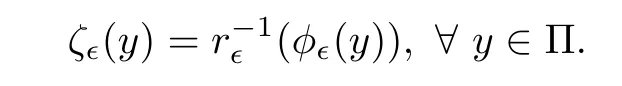
From Lemma 3.7,we obtain

Consider the set

where the function h1was already introduced in the definition of the setthen,for allthe setis nonempty.

From the above considerations,we can use Lemma 3.7,Lemma 2.4(A3),equality(3.28),and Lemma 3.10 to obtain＞0,such that for any∈∈(0,),the diagram

is well defined.In view of(3.28),for allwe can denote β∈(φ∈(y))=y+ϱ(∈,y)for all y ∈ Π,where|ϱ(∈,y)|＜uniformly in y ∈ Π.Define H(t,y)=y+(1 − t)ϱ(∈,y).Thus,H:[0,1]× Π → Πδis continuous.Obviously,H(0,y)= β∈(φ∈(y)),H(1,y)=y for all y ∈ Π.That is,H(t,y)is a homotopy between β∈◦φ∈=(β∈◦r∈)◦ζ∈and the inclusion map i:Π → Πδ.Therefore,

We can use Corollary 2.7 and Lemma 3.11,with c∈≤ c0+h1(∈)=c and K= ζ∈(Π),to conclude that Ψ∈has at least Catζ∈(Π)ζ∈(Π)critical points onCombining Proposition 2.5(d)with(3.29),we deduce that I∈has at least CatΠδ(Π)critical points in

4 Proof of Theorem 1.1

In this section,our main purpose is to show that the solutions obtained in Theorem 3.12 are indeed solutions of the original problem().The idea is to prove u∈(x)＜ a for all x ∈for∈small enough by using the Moser iterative method[13].The following lemma plays a fundamental role in the study of behavior of the maximum points of the solutions and can be found in[5].

Lemma 4.1Letbe a solution of problem(Q∈,g)with∈n→0+.Then,I∈n(un)→ c0and un∈ L∞(RN).Moreover,for any given γ ＞ 0,there exist R ＞ 0 and n0∈N such that

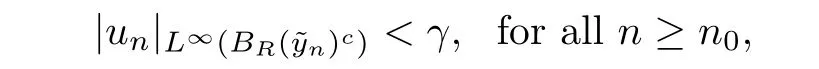
ProofThis result can be proven by using,with suitable modifications,the same arguments of[5].

Proof of Theorem 1.1We fix a small δ＞ 0 such that Πδ⊂ Λ.

ClaimThere is a＞0 such that for any solution u∈of the auxilary problem(Q∈,g),there holds

We argue by contradiction that there is a subsequence∈n→0+,un∈such that=0 and

It is clear that I∈n(un)→ c0as in Lemma 4.1.By Proposition 3.8,we can get a sequence⊂RNsuch that→y0∈Π.

For n large and letting r＞ 0 such that B2r(y0)⊂Λ,we get

and

which contradicts(4.2)and completes the claim.

Set∈δ=min,and let∈∈(0,∈δ)be fixed.We conclude from Theorem 3.12 that the problem(Q∈,g)has CatΠδ(Π)nontrival solutions.From(4.1)and the definition of g,we obtain g∈(·,u)=f(u).Thus,any solution of the problem(Q∈,g)obtained in Theorem 3.12 is also a solution of the problem().It is clear thatis a solution of the original problem(Q∈).Then,(Q∈)has at least CatΠδ(Π)nontrivial solutions.

Let{un}⊂ E∈nbe a sequence of solutions of the problem()with ∈n→ 0+.We now study the behavior of the maximum points of un.By(g1),there is a γ＞0 such that

By Lemma 4.1,we obtain R＞0 and()⊂RNsuch that

Up to a subsequence,we may also assume that

Indeed,if this is not the case,then,|un|L∞(RN)＜ γ,and therefore,it follows from=0 and(4.3)that

The above expression implies that ‖un‖∈n=0,which does not make sense,thus,(4.5)holds.

Let pn∈RNbe a maximum point of un,we conclude from(4.4)and(4.5)that pnbelongs toHence,for some qn∈BR(0).Sinceis a maximum point of.According to Proposition 3.8,we obtain

[1]Alves C O,Figueiredo G M.Multiplicity and concentration of positive solutions for a class of quasilinear problems via penalization methods.Adv Nonlinear Stud,2011,11(2):265–294

[2]Benci V,Cerami G.Multiple positive solutions for some elliptic problems via the Morse theory and the domain topology.Calcular of Variations,1993,2(1):29–48

[3]Damascelli L.Comparison theorems for some quasilinear degenerate elliptic operators and applications to symmetry and monotonity results.Annales Institut Henri Poincare Nonlinear Analysis,1998,15(4):493–516

[4]del Pino M,Felmer P L.Local mountain pass for semilinear elliptic problems in unbounded domains.Calc Var Partial Differ Equ,1996,4:121–137

[5]Figueiredo G M,Santos J R.Multiplicity and concentration behavior of positive solutions for a Schrödinger-Kirchhofftype problem via penalization method.Esaim Control Optimisation and Calculus of Variations,2014,20:389–415

[6]Figueiredo G M,Ikoma N,Júnior J R S.Existence and concentration result for the Kirchhofftype equation with general nonlinearities.Arch Rational Mech Anal,2014,213(3):931–979

[7]He X,Zou W.Existence and concentration behavior of positive solutions for a kirchhoffequation in R3.J Differential Equations,2012,252(2):1813–1834

[8]He Y,Li G.Standing waves for a class of Kirchhofftype problems in R3involving critical Sobolev exponents.Calc Var Partial Differential Equations,2015,54(3):3067–3106

[9]He Y,Li G,Peng S.Concentrating bounded states for Kirchhofftype problems in RNinvolving critical Sobolev exponents.Advanced Nonlinear Studies,2014,14(2):483–510

[10]Li G,Ye H.Existence of positive ground state solutions for the nonlinear Kirchhofftype equations in R3.J Differ Equ,2014,257(2):566–600

[11]Li G,Ye H.Existence of positive solutions for nonlinear Kirchhofftype equations in R3with critical Sobolev exponent.Math Meth Appl Sci,2015,37(16):2570–2584

[12]Lions P L.The concentration-compactness principle in the calculus of variations.The locally compact case,part II.Ann Inst H Poincare Anal Non Lineéaire,1984,1:223–283

[13]Moser J.A new proof of de Giorgís theorem concerning the regularity problem for elliptic differential equations.Commun Pure Appl Math,1960,13:457–460

[14]Szulkin A,Weth T.The method of Nehari manifold.Handbook of Nonconvex Analysis and Applications.Boston:International Press,2010:597–632

[15]Wang J,Tian L,Xu J,et al.Multiplicity and concentration of positive solutions for a Kirchhofftype problem with critical growth.J Differential Equations,2012,253(7):2314–2351

[16]Wang X.On concentration of positive bound states of nonlinear Schrödinger equations.Commun Math Phys,1993,53:229–244

[17]Willem M.Minimax Theorems.Boston:Birkhäusee,1996