CONVERGENCE OF HYBRID VISCOSITY AND STEEPEST-DESCENT METHODS FOR PSEUDOCONTRACTIVE MAPPINGS AND NONLINEAR HAMMERSTEIN EQUATIONS∗

Yekini SHEHU

Department of Mathematics,University of Nigeria,Nsukka,Nigeria

E-mail:yekini.shehu@unn.edu.ng

Olaniyi.S.IYIOLA

Department of Mathematics,Minnesota State University,Moorhead,Minnesota,USA

E-mail:olaniyi.iyiola@mnstate.edu

1 Introduction

Let H be a real Hilbert space and C be a nonempty closed convex subset of H.A mapping T:C → C is called a Lipschitz mapping if there exists L ≥ 0 such that‖Tx−Ty‖≤ L‖x−y‖, ∀x,y ∈ C.We say that T is nonexpansive if L=1.Furthermore,T is pseudocontractive if

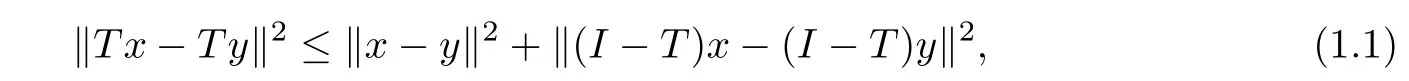
for all x,y∈C,where I is the identity mapping.For the rest of this article,the set of fixed point of T is defined by F(T):={x∈C:Tx=x}.

It is well known that the class of nonexpansive mappings is properly contained in the class of Lipschitz pseudocontractive mappings by this example from[1].

Example 1.1Let H=R2and suppose C={x∈ R2:‖x‖≤ 1}.Define C1={x∈andIf x=(a,b)∈ R2,we define x⊥ to be(b,−a)∈H.Define a map T:C →C by

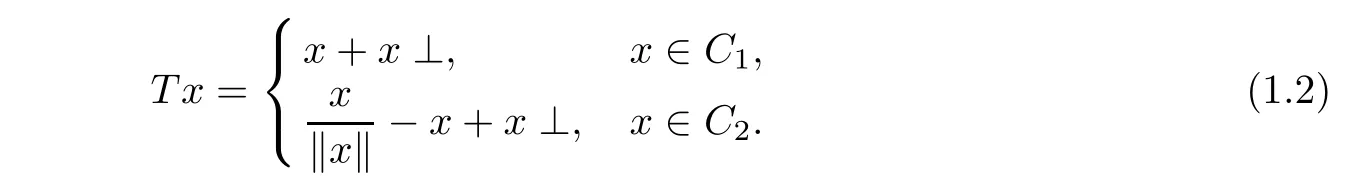
Then,T is a Lipschitz and pseudocontractive mapping but not a nonexpansive mapping.

Closely related to the class of pseudocontractive mappings is the class of monotone operators in Hilbert spaces.A mapping A:D(A)⊆H→H is called monotone if∀x,y∈D(A),

We remark here that T is a pseudocontractive mapping if and only if(I−T)is monotone.Interest in such mappings stems from their firm connection with equations of evolution.For more on monotone mappings and connections with evolution equations,the reader may consult any of the following references:Berinde[2,3],Browder[4],Chidume[5],Cioranescu[6],Kato[7],and Reich[8].Consequently,considerable research efforts,especially within the past 20 years or so,have been devoted to iterative methods for approximating the zeros of monotone mapping A or fixed point of pseudocontractive mapping T;see,for example,[9–18]and the references contained therein.

An iterative process commonly used for finding fixed points of nonexpansive maps is the following:For a convex subset C of a Hilbert space H and T:C → C,the sequenceis defined iteratively by x1∈C,

(ii)

The sequence of(1.4)is generally referred to as the Mann sequence in the light of[19].

It was not known whether or not the Mann iteration process would converge to fixed points of mappings belonging to this important class of Lipschitz pseudocontractive mappings.However,an iteration method which converges to a fixed point of a Lipschitz pseudocontractive self-map T of C was introduced in 1974 by Ishikawa.He proved the following theorem.

Theorem 1.2(Ishikawa,[20]) If C is a compact convex subset of a Hilbert space H,T:C −→C is a Lipschitzian pseudocontractive mapping,and x1is any point of C,then the sequence{xn}iteratively defined by

converges strongly to a fixed point of T,where{αn},{βn}are sequences of positive numbers satisfying the following conditions:

(i)0≤βn≤ αn＜1;

The question of whether the Mann iteration method can be used in the setting of Theorem 1.2 was eventually resolved in the negative by Chidume and Mutangadura[1]who gave an example of a Lipschitz pseudo-contractive self-map of a compact convex subset of a Hilbert space with unique fixed point for which no Mann sequence converges.

Motivated by the result of Yamada et al[21],Tian[22]considered the following general viscosity type iterative method for approximating the fixed point of a nonexpansive mapping:

Under certain approximate conditions,Tian[22]proved that the above sequence{xn}converges strongly to a fixed point of T,which also solves the variational inequality

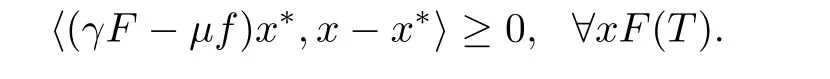
In[23],Shahzad and Zegeye introduced the following iterative scheme for approximation of fixed point of a pseudocontractive mapping T in real Hilbert spaces:

Under some appropriate conditions,they proved that the above sequence{xn}converges strongly to a minimum-norm point of fixed points of a Lipschitz pseudocontractive mapping T in real Hilbert spaces.

In the first part of this article,motivated by the works of Yamada et al[21],Tian[22],and[23],we introduce a new general viscosity type iterative algorithm for approximation of fixed points of Lipschitz pseudocontractive mappings and establish strong convergence theorem in real Hilbert spaces.In the second part,we shall adapt our iterative scheme for approximation of solution to a nonlinear Hammerstein integral equation.Finally,comparison is made with algorithm proposed in[24]through an example on Hammerstein equation.

2 Preliminaries

We shall make use of the following lemmas in the sequel.

Lemma 2.1Let H be a real Hilbert space.Then for∀x,y∈ H,we have

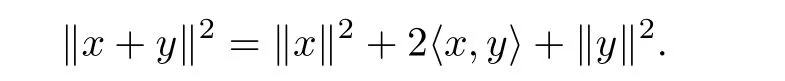
Lemma 2.2Let H be a real Hilbert space.Then,

for all x,y∈H.

Lemma 2.3([17,18]) Let C be a closed convex subset of a real Hilbert space H.Let T:C→C be a continuous pseudocontractive mapping.Then,

(i)F(T)is a closed convex subset of C;

(ii)(I−T)is demiclosed at zero,that is,if{xn}is a sequence in C such that xn⇀x and Txn−xn→0,as n→0,then x=Tx.

Lemma 2.4([25]) Let λ be a number in(0,1]and letµ ＞ 0.Let F:H → H be a κ-Lipschitz and η-strongly monotone mapping with κ ＞ 0 and η＞ 0.Associating with a nonexpansive mapping T:H→H,define the mapping Tλ:H→H by

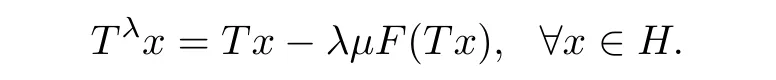
Then,Tλa contraction providedµ＜that is,

Lemma 2.5(see,for example,[3,26]) Letbe a sequence of nonnegative real numbers satisfying the following relation:

Lemma 2.6Let H be a real Hilbert space and let x,y∈H and t∈[0,1].Then,

3 Main Results

Theorem 3.1Let H be a real Hilbert space.Let F:H → H be a κ-Lipschitz and η-strongly monotone mapping with κ ＞ 0 and η ＞ 0,and V:H → H be a ρ-Lipschitz mapping with ρ ＞ 0.LetwhereLet T:H → H be an L-Lipschitz pseudocontractive mapping such that F(T)/= Ø.Suppose that{αn},{βn},and{γn}are sequences in(0,1).Given x1∈ H,let{xn}be defined by

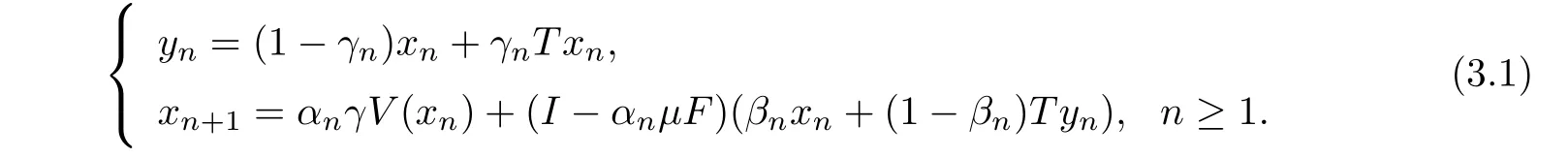
Assume that the following conditions are satisfied:

Then,the sequence{xn}converges strongly to x∗∈ F(T),where x∗=PF(T)(I−µF+γV)x∗is the unique solution of the variational inequality:

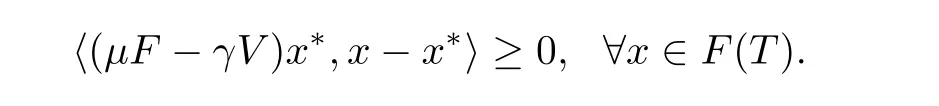
ProofLet F:H → H be a κ-Lipschitz and η-strongly monotone mapping,and V:H →H be a ρ-Lipschitz mapping,we have,for all x,y ∈ H,

This implies that PF(T)(I−µF+γV)is a contraction of H into itself,which implies that there exists the unique element x∗∈ H such that x∗=PF(T)(I−µF+γV)x∗.

Now,let zn= βnxn+(1− βn)Tyn, ∀n ≥ 1.Then,using Lemma 2.6,we have

By the fact that T is a pseudocontractive mapping,we obtain from(1.1)(noting that x∗=Tx∗)

By condition(ii),we have

This implies from(3.4)that

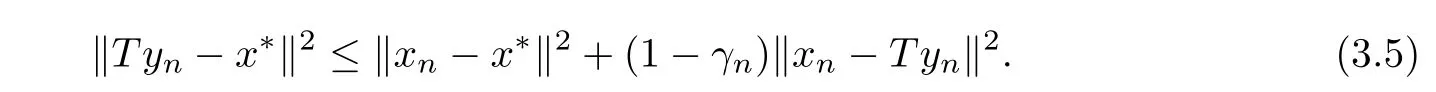
Substituting(3.5)into(3.3),we have

Now,from(3.1)and(3.6),we have

This implies that{xn}is bounded in H.Consequently,{yn}is bounded in H.

From(3.1)and Lemma 2.6,we have

Also,

By(3.1),(3.8),(3.9),and Lemma 2.2,we obtain(noting that T is a pseudocontractive mapping)

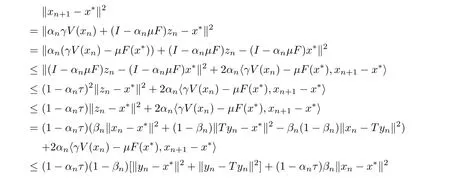
It then follows that

As{xn}and{V(xn)}are bounded,there exists M＞0 such that

Therefore,

The rest of the proof will be divided into two parts.

Case 1Suppose that there exists n0∈ N such thatis non-increasing.Then,converges and ‖xn− x∗‖ − ‖xn+1− x∗‖ → 0 as n → ∞.Then from(3.10),we obtain

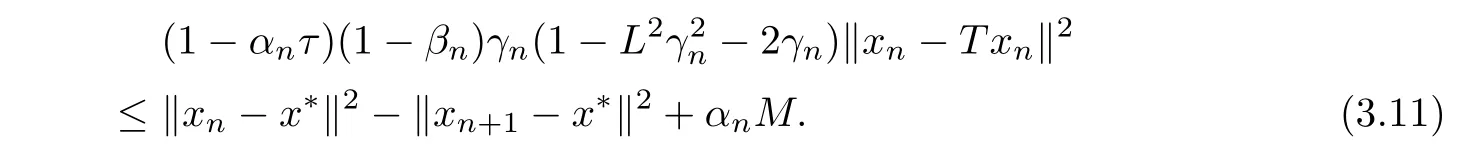
Using condition(ii),we obtain from(3.11)

This implies from(3.1)that

from which we obtain

So,

Therefore,

Hence,

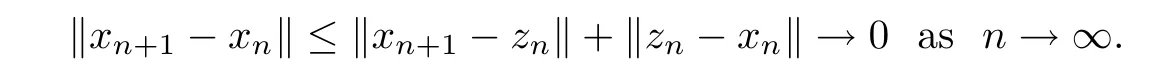
Because{xn}is bounded,there exists{xnk}of{xn}such that xnk⇀z∈H.From(3.12)and Lemma 2.3,we have z∈F(T).

Then,we obtain

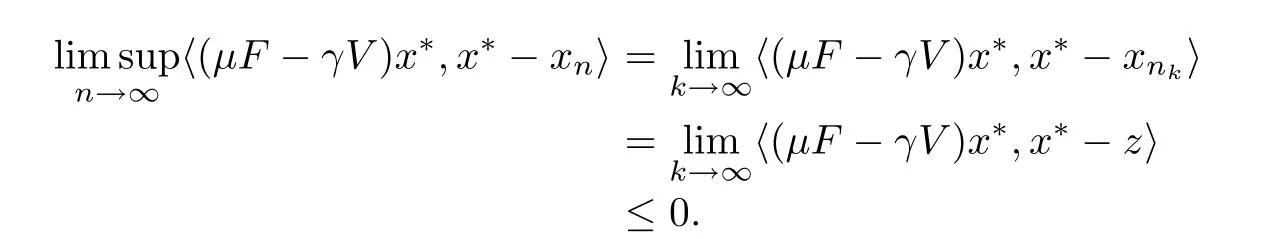
Finally,we show that{xn}converges strongly to x∗.By(3.1),Lemma 2.4,and Lemma 2.2,we have

This implies that

It is easy to see that δn→ 0 asUsing Lemma 2.5 in(3.13),we obtain

Thus,xn→x∗as n→∞.

Case 2Assume that{‖xn− x∗‖}is not monotonically decreasing sequence.Set Γn= ‖xn− x∗‖, ∀n ≥ 1 and let τ:N → N be a mapping for all n ≥ n0(for some n0large enough)by

Clearly,τ is a non decreasing sequence such that τ(n)→ ∞ as n → ∞ and

After a similar conclusion from(3.12),it is easy to see that

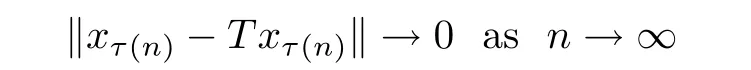
and

Because{xτ(n)}is bounded,there exists a subsequence of{xτ(n)},still denoted by{xτ(n)}which converges weakly to z∈F(T).By the similar argument as above in Case 1,we conclude immediately thatFrom(3.13),we have

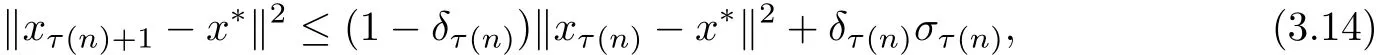
which implies that(noting that Γτ(n)≤ Γτ(n)+1and ατ(n)＞ 0)

This implies that

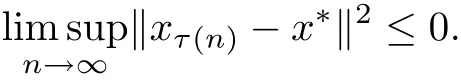
Thus,

Again from(3.14),we obtain

Therefore,

Furthermore,for n ≥ n0,it is easy to see that Γτ(n)≤ Γτ(n)+1if n/= τ(n)(that is,τ(n)＜ n),because Γj≥ Γj+1for τ(n)+1 ≤ j≤ n.As a consequence,we obtain,for all n ≥ n0,

Hence,limΓn=0,that is,{xn}converges strongly to¯x.This completes the proof.

4 Application to Integral Equations of Hammerstein Type

A nonlinear integral equation of Hammerstein type(see,for example,Hammerstein[27])is one of the form

where dy is a σ- finite measure on the measure space Ω;the real kernel k is defined on Ω × Ω,and f is a real-valued function defined on Ω×R and is,in general,nonlinear.If we now define an operator K by

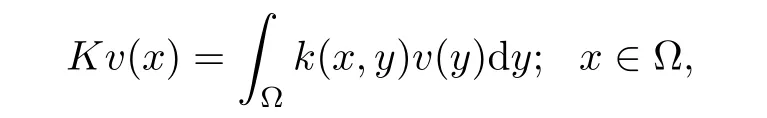
and the so-called superposition or Nemytskii operator by Gu(y):=f(y,u(y)),then,the integral equation(4.1)can be put in the operator theoretic form as follows:

Nonhomogeneous Hammerstein integral equation

can be reduced to the homogeneous equation(4.1)if we set

Consequently,we can reduce the nonhomogeneous operator equation v+KHv=b,where Hv(y):=g(y,v(y)),to the homogeneous equation(4.2).Hence,it is sufficient to consider the homogeneous problems.

Interest in equation(4.2)stems mainly from the fact that several problems that arise in differential equations;for instance,elliptic boundary value problems whose linear parts possess Green’s functions can,as a rule,be transformed into the form(4.2).

Example 4.1Consider the differential equation

The corresponding Hammerstein integral equation is

Equations of Hammerstein type play a crucial role in the theory of optimal control systems and in automation and network theory(see,for example,Dolezale[28]).Several existence and uniqueness theorems have been proved for equations of the Hammerstein type(see,for example,Brezis and Browder[29–31],Browder[4],Browder and De Figueiredo[32],Browder and Gupta[33],Chepanovich[34],and De Figueiredo[35]).The Mann iteration scheme(see,for example,Mann[19])has successfully been employed(see,for example,the recent monographs of Berinde[2]and Chidume[5]).The recurrence formulas used involved K−1which is also assumed to be strongly monotone and this,apart from limiting the class of mappings to which such iterative schemes are applicable,is also not convenient in applications.Part of the difficulty is the fact that the composition of two monotone operators need not be monotone.

Iterative approximation of solutions to nonlinear integral equations of Hammerstein type(4.1)and(4.2)were studied in the literature by several authors under various assumptions on f(·,·)and k(·,·).We refer the reader to,for instance,the articles[36–48]and the references therein.

We need the following lemma in our next theorem.

Lemma 4.2([24])Let H be a real Hilbert space.Let K,G:H→H be monotone mappings with D(G)=D(K)=H.Let T:H×H→H×H be defined by T(u,v):=(u−Gu+v,v−Kv−u)for all(u,v)∈H×H,then T is pseudocontractive.Moreover,if the Hammerstein equation u+KGu=0 has a solution in H,then u∗is a solution of u+KGu=0 if and only if(u∗,v∗)∈ F(T),where v∗=Gu∗.

We now adapt our iterative scheme(3.1)to solve a nonlinear integral equation of Hammerstein type.

Let W:=H ×H with the norm ‖w‖W:=(‖u1‖2+‖v1‖2)for arbitrary w=[u1,v1]∈ W and for arbitrary x=[u1,v1],y=[u2,v2]in W,the inner product〈·,·〉Wis given by 〈x,y〉E=〈u1,u2〉H+ 〈v1,v2〉H.

We make the following obvious remark but we give the details for the sake of completeness.

Remark 4.3Define F:W→W by Fw=F(u,v):=(f1(u),f2(v)),u,v∈H,where fi:H → H are κi-Lipschitz and ηi-strongly monotone mapping with κi＞ 0 and ηi＞ 0 and i=1,2.Observe that if x=[x1,y1],y=[x2,y2]∈W,then we have

where η :=min{η1,η2}.Thus,F is η-strongly monotone.Furthermore,

Similarly,define a map V:W→W by V w=V(u,v):=(h1(u),h2(v)),u,v∈H,where hi:H → H is ρi-Lipschitz mapping with ρi＞ 0,i=1,2.Then,it can be shown that V is ρ-Lipschitz mapping with

Using the above arguments,we state and prove the following theorem for approximation of solution of a nonlinear integral equation of Hammerstein type.

Theorem 4.4Let H be a real Hilbert space.Let K,G:H→H be Lipschitz monotone mappings such that D(G)=D(K)=H.Assume that u∗∈ H is a solution of Hammerstein equation u+KGu=0 and Ω is the set of solutions with v∗=Gu∗and Ω /= Ø.Define a mapping T:W→W as

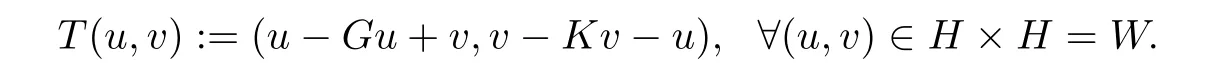
Let F:W → W be a κ-Lipschitz and η-strongly monotone mapping with κ ＞ 0 and η ＞ 0,and V:W → W be a ρ-Lipschitz mapping with ρ ＞ 0.Let 0 ＜ µ ＜and 0＜ γρ ＜ τ,where τ=Let Twn=(un−Gun+vn,vn−Kvn−un),wn=(un,vn)∈ W, ∀n≥1.Suppose that{αn},{βn},and{γn}are sequences in(0,1).Given w1=(u1,v1)∈ W,let{wn}be defined by

Assume that the following conditions are satisfied:

where L is the Lipschitz rank of T.Then,the sequence{xn}converges strongly to x∗∈ F(T),where x∗=PF(T)(I−µF+γV)x∗is the unique solution of the variational inequality:

ProofIf K,G:H→H are monotone mappings,then the map T:H×H→H×H defined by T(u,v):=(u−Gu+v,v−Kv−u), ∀(u,v)∈H×H=W,by Lemma 4.2,is a pseudocontractive mapping with F(T)=Ω.Furthermore,if K and G are LKand LGLipschitz mappings,respectively,for all[u1,v1],[u2,v2]∈W and for some d＞0,we obtain

This implies that T is a Lipschitz pseudocontractive mapping on W=H×H.By Theorem 3.1,we have our desired conclusion.

5 Numerical Example

In this section,we consider an example related to the Hammerstein equation and numerically show how our algorithm is applicable.We also compare our result with that of Ofoedu and Onyi[24].All codes were written in Matlab 2014b and run on Dell i-5 Dual-Core laptop.

Example 5.1In our iterative scheme(4.4),let us take F=I,V=12I.Then,ρ=1 and η=1=κ.Hence,

Let us chooseµ =1 and then we haveAs 0＜ γρ ＜ τ,we have γ ∈(0,2).Without loss of generality,let us assume that γ =1.

We shall consider two cases.

Case ILet H=R with the inner product defined by 〈x,y〉=xy for all x,y ∈ R and the standard norm|·|.Then,W=R×R.Let us consider the Hammerstein equation u+KGu=0 in R with Ku=max{0,u}=Gu.Observe that u∗=0 is a solution to the Hammerstein equation.

The mapping T:R2→R2is defined by Tw=T(u,v)=(u−max{0,u}+v,v−max{0,v}−u),u,v ∈ R.Let

Then,observe that conditions(i)and(ii)in Theorem 4.4 are satisfied and our iterative scheme(4.4)becomes

If yn=(tn,sn), ∀n≥1,then we have

For Case I,the scheme(3.15)of Ofoedu and Onyi[24]with T(un,vn)=(un−Gun+vn,vn−Kvn−un)=(un−max{0,un}+vn,vn−max{0,vn}−un),(un,vn)∈R2becomes

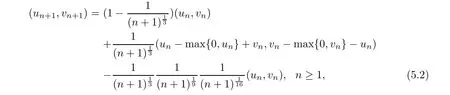
We compare our scheme(5.1)with scheme(5.2)of Ofoedu and Onyi[24]for different choices of w1=(u1,v1) ∈ R × R and usestopping criterion.The results are reported in Table 1 and Figures 1–4.for

Table 1 Case I:Algorithm 5.1 and Ofoedu and Onyi’s Algorithm 5.2

Figure 1 Case I:w1=(3.2519,−7.5493)

Figure 2 Case I:w1=−(1.0224,2.4145)

Figure 3 Case I:w1=(−10.8906,0.3256)

Figure 4 Case I:w1=(154.4212,8.5931)

Case IILet H=L2([0,1])with the inner product defined byfor all x,y ∈ L2([0,1])and the standard normThen,W=L2([0,1])×L2([0,1]).Let us consider the Hammerstein equation u+KGu=0 in L2([0,1])with

Observe that u∗=0 is a solution to the Hammerstein equation.

The mapping T:L2([0,1])×L2([0,1])→ L2([0,1])×L2([0,1])is defined by Tw=T(u,v)=(u−Gu+v,v−Kv−u),w=(u,v)∈ L2([0,1])×L2([0,1]).Let αn=and

Let Twn=T(un,vn)=(un−Gun+vn,vn−Kvn−un)and Tyn=T(tn,sn)=(tn−Gtn+sn,sn−Ksn−tn)with G and K given in(5.3).Our iterative scheme(4.4)in Theorem 4.4 becomes

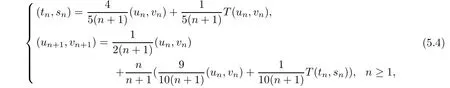
Again,for Case II,the scheme(3.15)of Ofoedu and Onyi[24]becomes

We also compare our scheme(5.4)with scheme(5.5)of Ofoedu and Onyi[24]for different choices of w1=(u1,v1)∈ L2([0,1])× L2([0,1])and use10−6for stopping criterion.The results are reported in Table 2 and Figures 5–6.

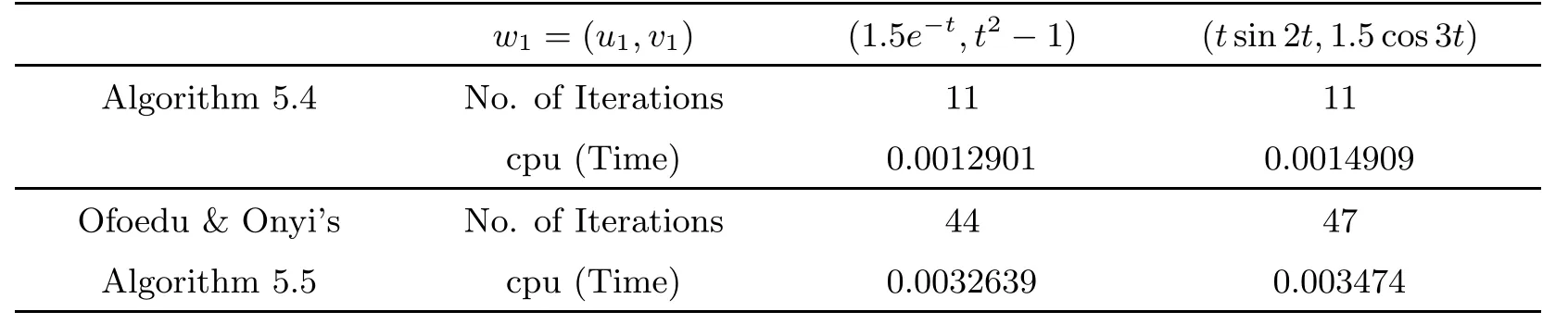
Table 2 Case II:Algorithm 5.4 and Ofoedu and Onyi’s Algorithm 5.5

Figure 5 Case II:w1=(1.5e−t,t2−1)

Figure 6 Case II:w1=(tsin2t,1.5cos3t)

Remark 5.2(1)The numerical results from both cases considered show that both Algorithm(5.2)and Ofoedu and Onyi’s algorithm are very efficient,consistent and easy to implement.Irrespective of the choice of initial guess,there is no significant difference in the number of iteration and the cpu time taken.This is because of the consequence of the linearity of the mapping wn→ wn+1and the stopping criterion.

(2)We also observe from the example that our algorithm is more than three times faster than Ofoedu and Onyi’s algorithm for Case I and Case II.While the number of iterations required for our algorithm is about one-third of the number of iterations required for Ofoedu and Onyi’s algorithm in both cases.

AcknowledgementsThe researchwas carried out when the First Author was an Alexander von Humboldt Postdoctoral Fellow at the Institute of Mathematics,University of Wurzburg,Germany and he is grateful to the Alexander von Humboldt Foundation,Bonn for the fellowship and the Institute of Mathematics,University of Wurzburg,Germany for the hospitality and facilities.

[1]Chidume C E,Mutangadura S.An example on the Mann iteration method for Lipschitz pseudocontractions.Proc Amer Math Soc,2001,129(8):2359–2363;MR 20022f:47104

[2]Berinde V.Iterative approximation of fixed points,Springer Verlag Series:Lecture Notes in Mathematics,2007,1912:ISBN 978-3-540-72233-5

[3]Berinde V.Iterative approximation of fixed points.Editura Efemeride Baia Mare,2002

[4]Browder F E.Nonlinear mappings of nonexpansive and accretive type in Banach spaces.Bull Amer Math Soc,1967,73:875–882

[5]Chidume C E.Geometric properties of Banach spaces and nonlinear iterations.Springer Verlag Series:Lecture Notes in Mathematics,2009,1965(17):326p,ISBN 978-1-84882-189-7

[6]Cioranescu I.Geometry of Banach spaces,duality mappings and nonlinear problems.Dordrecht:Kluwer Academic,1990

[7]Kato T.Nonlinear semigroups and evolution equations.J Math Soc Japan,1967,19:508–520

[8]Reich S.Strong convergence theorems for resolvents of accretive operators in Banach spaces.J Math Anal Appl,1994,183:118–120

[9]Chidume C E,Shehu Y.Strong convergence theorems for the approximation of fixed points of demicontinuous pseudocontractive mappings.J Appl Anal,2013,19:213–229

[10]Ceng L C,Petrusel A,Yao J-C.Strong convergence of modified implicit iterative algorithms with perturbedmappings for continuous pseudocontractive mappings.Appl Math Comput,2009,209(2):162–176

[11]Cho S Y,Qin X,Kang S M.Hybrid projection algorithms for treating common fixed points of a family of demicontinuous pseudocontractions.Appl Math Lett,2012,25:584–587

[12]Lan K Q,Wu J H.Convergence of approximates for demicontinuous pseudo-contractive maps in Hilbert spaces.Nonlinear Anal,2002,49(6):737–746

[13]Morales C H,Jung J S.Convergence of paths for pseudocontractive mappings in Banach spaces.Proc Amer Math Soc,2000,128(11):3411–3419

[14]Ofoedu E U,Zegeye H.Further investigation on iteration processes for pseudocontractive mappings with application.Nonlinear Anal,2012,75:153–162

[15]Yao Y H,Liou Y C,Marino G.A hybrid algorithm for pseudo-contractive mappings.Nonlinear Anal,2009,71:4997–5002

[16]Yu Y.An Iterative Algorithm on Approximating Fixed Points of Pseudocontractive Mappings.Journal of Applied Mathematics,2012,Article ID 341953:11 pages

[17]Zhang Q B,Cheng C Z.Strong convergence theorem for a family of Lipschitz pseudocontractive mappings in a Hilbert space.Math Comput Model,2008,48(3/4):480–485

[18]Zhou H.Strong convergence of an explicit iterative algorithm for continuous pseudo-contractives in Banach spaces.Nonlinear Anal,2009,70:4039–4046

[19]Mann W R.Mean value methods in iterations.Bull Amer Math Soc,1953,4:506–510

[20]Ishikawa S.Fixed points by a new iteration method.Proc Amer Math Soc,1974,44(1):147–150

[21]Yamada I,Butnariu D,Censor Y,Reich S.The hybrid steepest descent method for the variational inequality problems over the intersection of fixed points sets of nonexpansive mappings//Inherently Parallel Algorithms in Feasibility and Optimization and Their Application.Amsterdam:North-Holland,2001

[22]Tian M.A general iterative algorithm for nonexpansive mappings in hilbert spaces.Nonlinear Anal,2010,73:689–694

[23]Shahzad N,Zegeye H.Approximating a common point of fixed points of a pseudocontractive mapping and zeros of sum of monotone mappings.Fixed Point Theory Appl,2014,2014:85

[24]Ofoedu E U,Onyi C E.New implicit and explicit approximation methods for solutions of integral equations of Hammerstein type.Appl Math Comput,2014,246:628–637

[25]Xu H K,Kim T H.Convergence of hybrid steepest-descent methods for variational inequalities.J Optim Theory Appl,2003,119:185–201

[26]Xu H K.Iterative algorithm for nonlinear operators.J London Math Soc,2002,66(2):1–17

[27]Hammerstein A.Nichtlineare integralgleichungen nebst anwendungen.Acta Math,1930,54:117–176

[28]Dolezale V.Monotone operators and its applications in automation and network theory.New York:Studies in Automation and control(Elesevier Science Publ),1979

[29]Brézis H,Browder F E.Some new results about Hammerstein equations.Bull Amer Math Soc,1974,80:567–572

[30]Brézis H,Browder F E.Existence theorems for nonlinear integral equations of Hammerstein type.Bull Amer Math Soc,1975,81:73–78

[31]Brézis H,Browder F E.Nonlinear integral equations and system of Hammerstein type.Advances in Math,1975,18:115–147

[32]Browder F E,Figueiredo D G,Gupta P.Maximal monotone operators and a nonlinear integral equations of Hammerstein type.Bull Amer Math Soc,1970,76:700–705

[33]Browder F E,Gupta P.Monotone operators and nonlinear integral equations of Hammerstein type.Bull Amer Math Soc,1969,75:1347–1353

[34]Chepanovich R Sh.Nonlinear Hammerstein equations and fixed points.Publ Inst Math(Beograd)N S,1984,35:119–123

[35]De Figueiredo D G,Gupta C P.On the variational methods for the existence of solutions to nonlinear equations of Hammerstein type.Bull Amer Math Soc,1973,40:470–476

[36]Banas J.Integrable solutions of Hammerstein and Uryshon integral equations.J Aust Math Soc A,1989,46:61–68

[37]Banas J,Knap Z.Measure of weak noncompactness and nonlinear integral equations of convolution type.J Math Anal Appl,1990,146:353–362

[38]Chidume C E,Ofoedu E U.Solution of nonlinear integral equations of Hammerstein type.Nonlinear Anal,2011,74:4293–4299

[39]Chidume C E,Shehu Y.Strong convergence theorem for approximation of solutions of equations of Hammerstein type.Nonlinear Anal,2012,75:5664–5671

[40]Chidume C E,Shehu Y.Iterative approximation of solutions of equations of Hammerstein type in certain Banach spaces.Appl Math Comput,2013,219:5657–5667

[41]Chidume C E,Zegeye H.Approximation of solutions nonlinear equations of Hammerstein type in Hilbert space.Pro Amer Math Soc,2005,133:851–858

[42]Emmanuele G.Integrable solutions of a functional-integral equation.J Integral Equations Appl,1992,4:89–94

[43]Emmanuele G.An existence theorem for Hammerstein integral equations.Port Math,1994,51:607–611

[44]Latracha K,Taoudi M A.Existence results for a generalized nonlinear Hammerstein equation on L1spaces.Nonlinear Anal,2007,66:2325–2333

[45]Shehu Y.Strong convergence theorem for integral equations of Hammerstein type in Hilbert spaces.Appl Math Comput,2014,231:140–147

[46]Shehu Y.Convergence theorems for maximal monotone operators and fixed point problems in Banach spaces.Appl Math Comput,2014,239:285–298

[47]Hulbert D S,Reich S.Asymptotic Behavior of Solutions to Nonlinear Volterra Integral Equations.J Math Anal Appl,1984,104:155–172

[48]Reich S.Admissible Pairs and integral Equations.J Math Anal Appl,1987,121:79–90