FINITE-TIME H∞CONTROL FOR A CLASS OF MARKOVIAN JUMPING NEURAL NETWORKS WITH DISTRIBUTED TIME VARYING DELAYS-LMI APPROACH∗

P.BASKAR

New Horizon College of Engineering,Marathhalli,Bangalore 560103,India

S.PADMANABHAN

RNS Institute of Technology,Channasandra,Bangalore 560098,India

M.SYED ALI

Department of Mathematics,Thiruvalluvar University,Vellore,Tamilnadu 632115,India

E-mail:syedgru@gmail.com

1 Introduction

In recent years,neural networks(especially switched neural networks,recurrent neural networks,Hop field neural networks,and cellular neural networks)have been successfully applied in many areas such as pattern recognition,associative memory,image processing,fault diagnosis,and combinatorial optimization.Many researchers focused on studying the existence,uniqueness,and global robust asymptotic stability of the equilibrium point in the presence of time delays and parameter uncertainties for various classes of nonlinear neural networks(see[1–6]).When a neural network incorporates abrupt changes in its structure,a Markovian jump system is very appropriate to describe its dynamics.Thus,the problem of stochastic robust stability for uncertain delayed neural networks with Markovian jumping parameters is investigated via LMI technique in[7–13].

The linear matrix inequality approach is one of the most extensively used in recent publications.For instance,in[14–18],a class of switched Hop field neural networks with time-varying delay by integrating the theory of switched systems with neural networks with time-varying delay are reported,global exponential stability conditions for switched Hop field neural networks with time-varying delay are addressed on the basis of the Lyapunov-Krasovskii functional approach,and a delay-dependent robust stability criteria are presented by employing LMIs and free weighting matrices methods.

In practical implementations,uncertainties are inevitable in neural networks because of the existence of modeling errors and external disturbance.It is important to ensure the neural networks system is stable under these uncertainties(see[19–21]).Both time delays and uncertainties can destroy the stability of neural networks in an electronic implementation.Therefore,it is of great theoretical and practical importance to investigate the robust stability for delayed neural networks with uncertainties(see[22–26]).

In the recent years,H∞concept was proposed to reduce the effect of the disturbance input on the regulated output to within a prescribed level.Hence,H∞finite time boundness for switched neural networks with time varying delays takes considerable attention[27–33].Usually,some performance indexes,that is,H∞and L∞,are employed to deal with external disturbances.Many results are developed with these performance indexes(see[34–39]references therein).

To the best of authors knowledge,there is no results available on the H∞control for Markovian jumping neutral-type neural networks(MJNNs)time varying delays.Motivated by this,in this article,we analyze the adaptive finite time stability for the MJNNs.LMI-matrixbased criteria for determining finite time stability for the MJNNNs are developed.

This article is organized as follows.In Section 2,we presents problem formulation,notations,definitions,and technical lemmas.In Section 3,stability conditions are proposed for delayed neural network systems;a reliable H∞controller is derived to guarantee the exponential stability with uncertainties of the resulting closed-loop neural network systems.Section 4 illustrative examples and comparison results are given to show the conservativeness and effectiveness of the proposed results.

2 Notations

Throughout this article,we will use the notation A＞0 to denote that the matrix A is a symmetric and positive definite matrix.Let(⊗,F,{Ft}t≥0,P)be a complete probability space with a filtration{Ft}t≥0satisfying the usual conditions(it is right continuous and F0contains all P-null sets);be the family of all bounded,F0-measurable,C([−τ,0];Rn)-valued random variables ξ={ξ(θ): −τ≤ θ ≤ 0}such thatThe mathematical expectation operator with respect to the given probability measure P is denoted by E{·}.The shorthand diag{···}denotes the block diagonal matrix. ‖ ·‖ stands for the Euclidean norm.Moreover,the notation∗always denotes the symmetric block in one symmetric matrix.Let{ηt,t≥ 0}be a homogeneous, finite-state Markovian process with right continuous trajectories and taking values in finite set S={1,2,···,s}with a given probability space(⊗,F,P)and the initial model η0. Π =[πij]s×s,i,j ∈ S,which denotes the transition rate matrix with transition probability

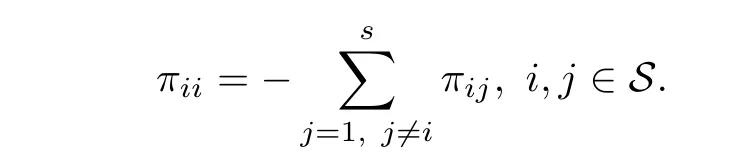
2.1 Problem formulation and preliminaries

Consider the following Markovian jumping neural networks of neutral type with distributed time varying delays

where x(t)=[x1(t),x2(t),···,xn(t)]T∈ Rnis the state,u(t) ∈ Rlis the control input,w(t)∈ Rnis the disturbance input which belongs to L2[0,∞),and z(t)∈ Rqis the controlled output.f(x(t))is the neuron activation function,and φ(θ)is a continuous vectorvalued initial function.For eachin which Diare a positive diagonal matrices,Ai,Bi,Ci,Di,Ei,F1i,F2i,Gi,J1i,J2i∈ Rn×nare the weight connection matrices with appropriate dimensions,and ΔAi(t),ΔBi(t),ΔCi(t),ΔDi(t),ΔJ1i(t)are uncertain real-valued matrices.The variables τ(t),σ(t),and ρ(t)represent respectively the time varying delay,distributive,and neutral delays satisfyingandand d2are positive constants,and

Assumption 1Assume that the uncertainties are norm-bounded and of the form

where M1i,M2i,M3i,M4i,M5iare known real-valued constant matrices with appropriate dimensions,Ωiare unknown and possibly time-varying matrix with Lebesgue measurable elements satisfying

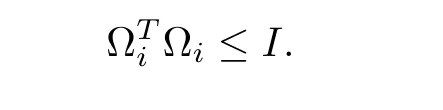
Assumption 2For a given time constant Tf,the external disturbance w(t)satisfies

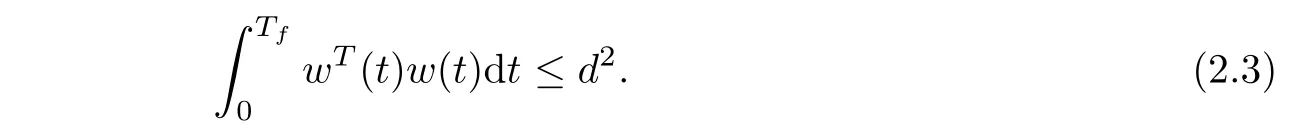
Assumption 3The activation functions satisfy the following condition,for any i=1,2,···,n,there exist constantssuch that

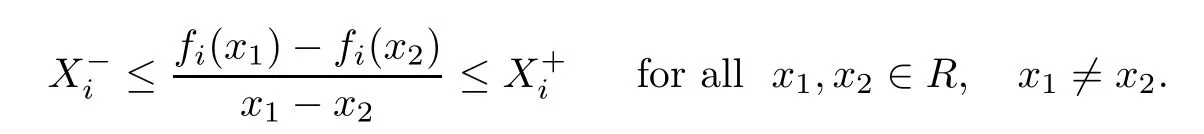
For presentation convenience,we denote

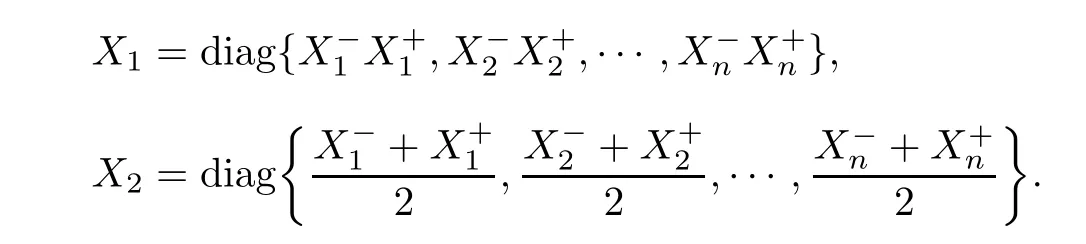
Definition 2.1([8]Finite-time stability) For a given time constant τ＞0,neural networks(2.1)is said to be stochastically finite-time stable with respect toif

where c2＞ c1＞ 0,R is a positive definite matrix,and η(t)is a switching signal.

Remark 2.2Consider neural network(2.1)with u(t)≡0 and w(t)≡0,the neural networks is said to be uniformly finite-time stable with respect toif(2.4)holds.

Definition 2.3([37]Finite-time boundedness) For a given time constant Tf,neural networks(2.1)with u(t)≡ 0 is said to be finite-time bounded with respect toif condition(2.4)holds,where c2＞ c1＞ 0,R is a positive definite matrix,η(t)is a switching signal,and w(t)satisfy(2.3).

Definition 2.4([37]Finite-time H∞performance) For a given time constant Tf,neural networks(2.1)is said to be robust finite-time H∞performance with respect toR,η(t))if the networks is finite-time bounded and the following inequality holds

Definition 2.5([33]Robust finite-time H∞control) For a given time constant Tf,neural networks(2.1)is said to be robust finite-time stabilizable with H∞disturbance attenuation level γ,if there exists a controller u(t)=Kη(t)x(t),t∈ (0,Tf],such that(i)The corresponding closed-loop neural network is finite-time bounded;(ii)Under zero initial condition,inequality(2.5)holds for any w(t)satisfying Assumption 2.

Lemma 2.6([25]) For any constant matrix M ∈ Rn×n,M=MT＞ 0,scalar η2＞ η1≥ 0,and vector function w:[η1,η2] → Rnsuch that the integrations concerned are well defined,then we have

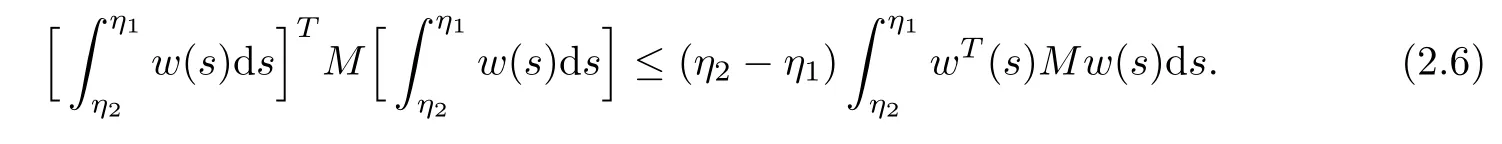
Lemma 2.7([40]) Let U,V,W,and X be real matrices of appropriate dimensions with X satisfying X=XT,then for all VTV≤I,X+UV W+UTVTWT＜0,if and only if there exists a scalar δ＞ 0 such that X+ δUUT+ δ−1WTW ＜ 0.

3 Main Results

3.1 Finite-time boundedness analysis

In this section,we consider the problem of finite time boundedness for the following neural networks

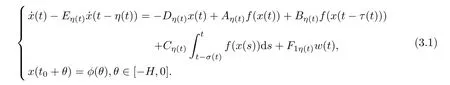
Theorem3.1Consider the neural networks(3.1),and letIf there exist positive scalars α,λk,(k=1,2,···,7),positive definite matrices Pi,Q1,Q2,Q3,S1,S2,T,and positive diagonal matrices U1,U2with appropriate dimensions,such that the following LMI holds,

with

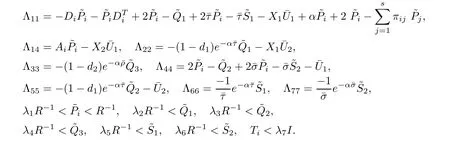
ProofChoose the following Lyapunov-Krasovskii functional

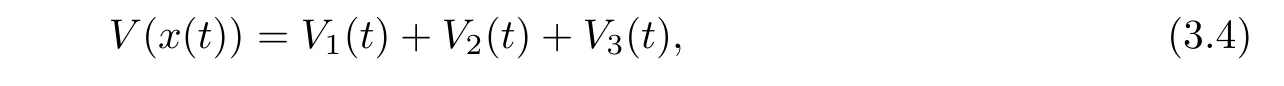
where

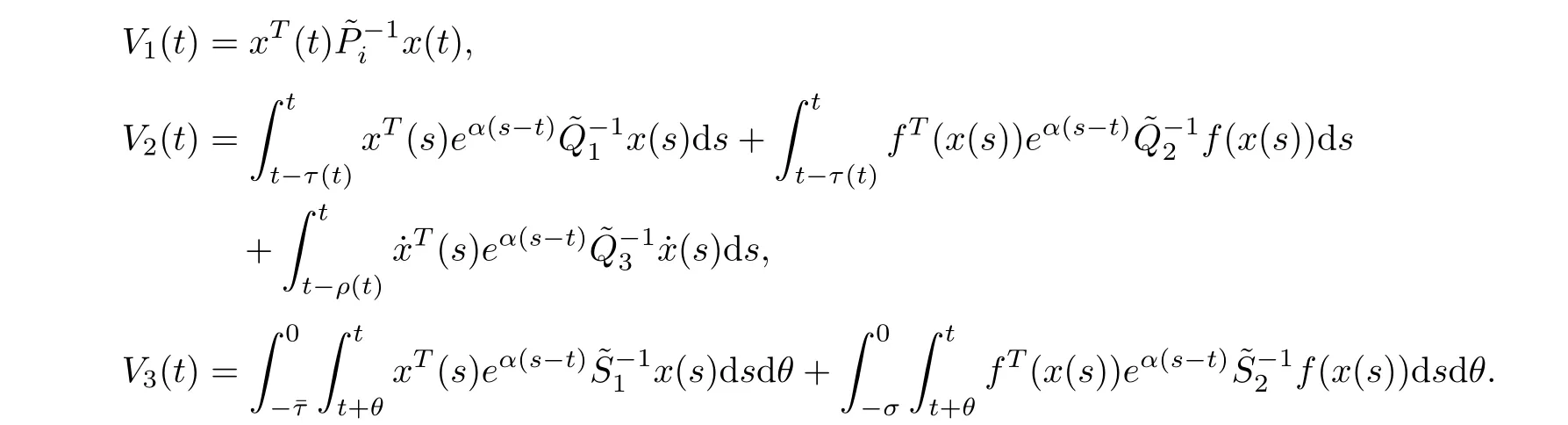
Taking the derivative of the V(t)along the trajectory of(3.1),we have

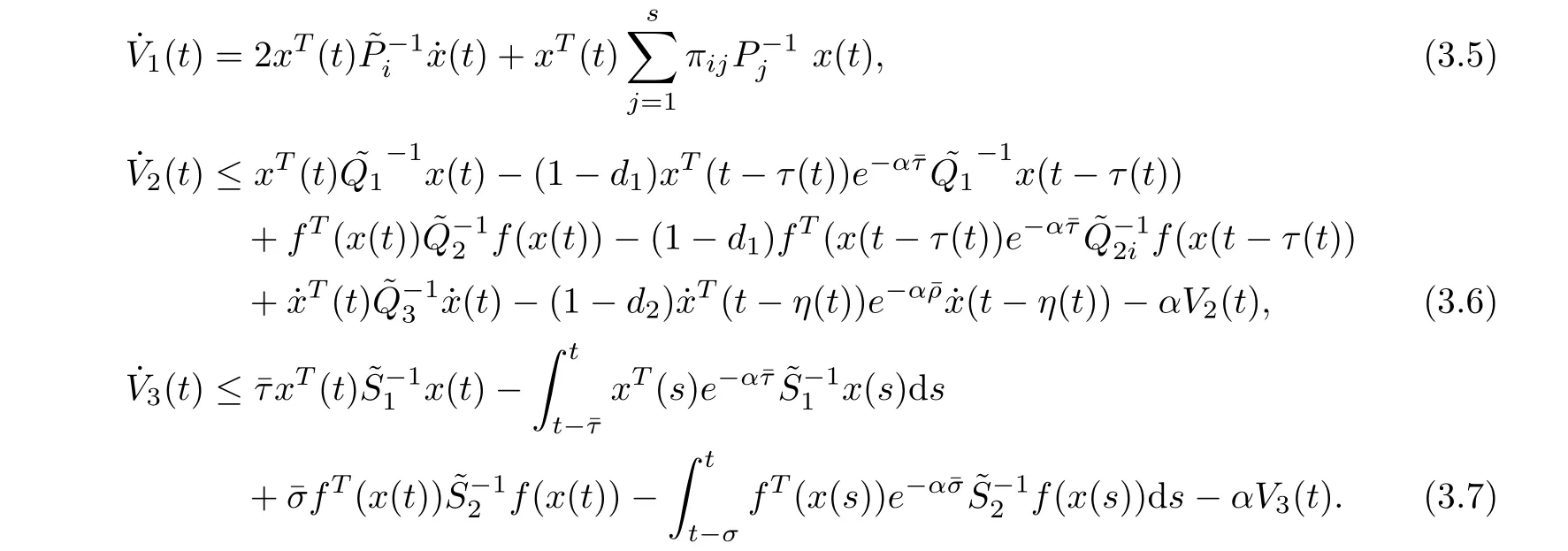
Using Lemma 2.6,we obtain

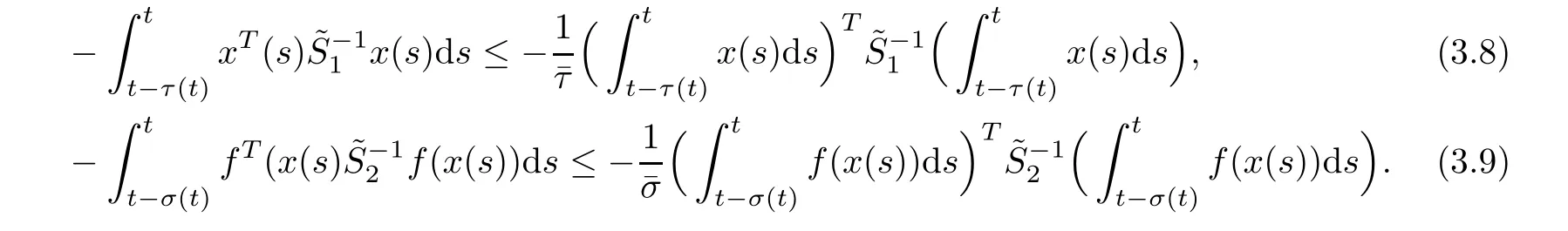
By Assumption 3,it is obtained that

can be compactly written as

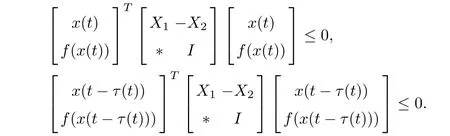
Then,for any positive diagonal matrices U1and U2,the following inequalities hold true

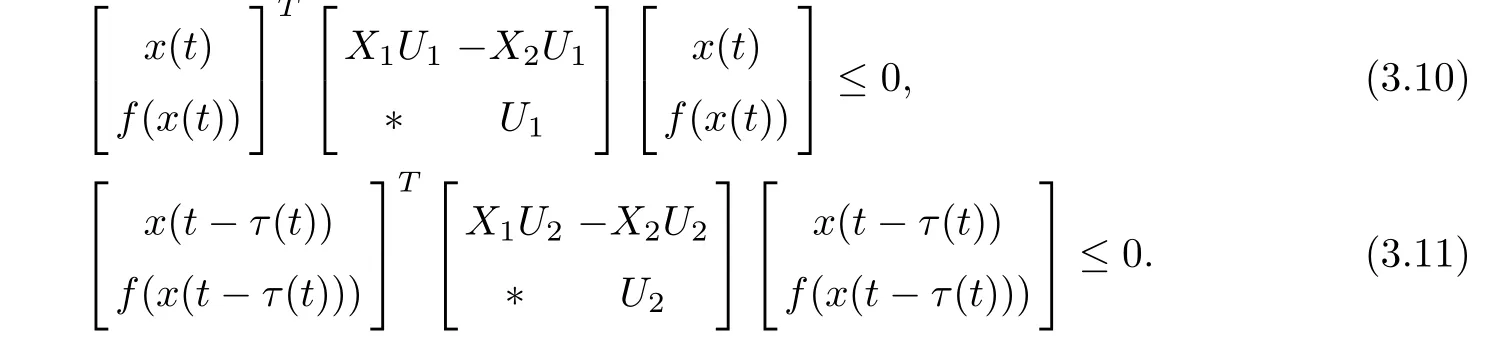
Combining and adding(3.4)–(3.11),we obtain

here

with

Using Schur complement lemma,we have

pre-multiply and post multiply by the term of(3.14)by diagand then by using fact that,and replacingwe get Λ＜0.From(3.2),we have

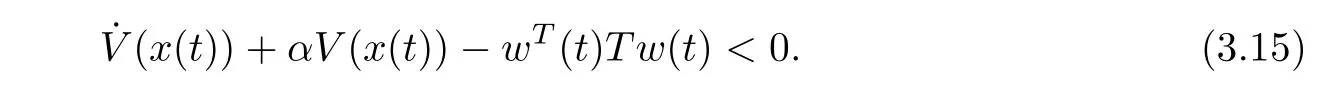
Then,

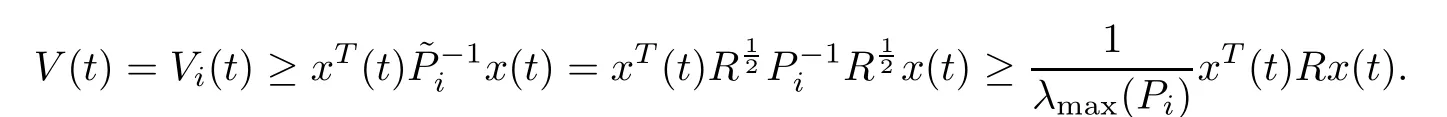
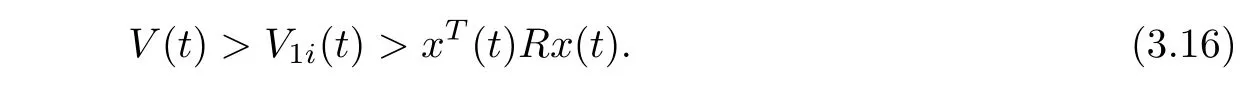
On the other hand,

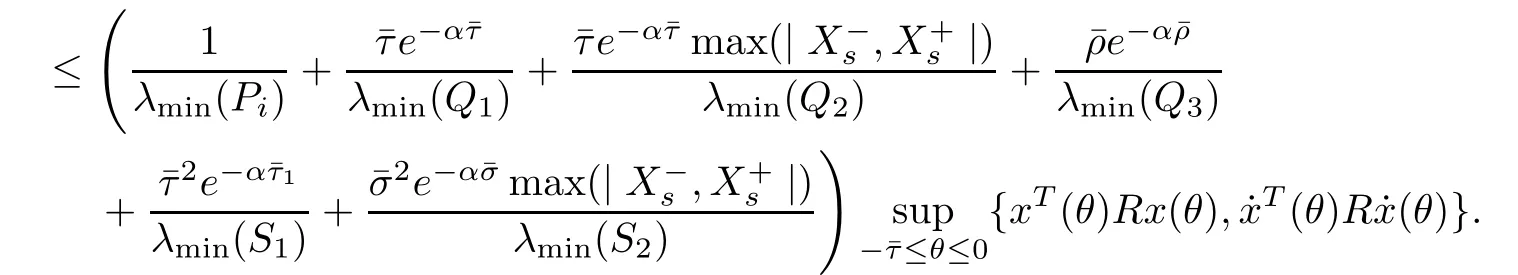
We obtain

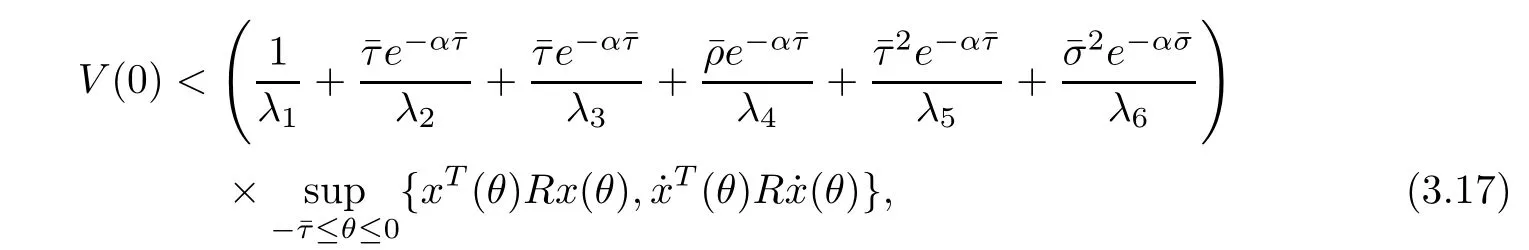
then it holds that

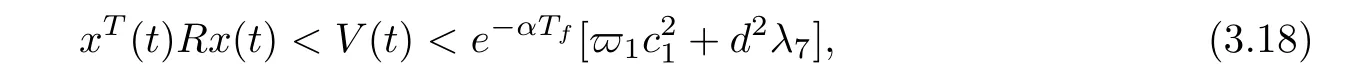
here

By Definition 2.1,we have

According to Definition 2.3,we know that neural networks(3.1)is finite-time bounded with respect toThus,the proof is completed.

Corollary 3.2Consider neural networks(3.1)withThen,the networks is finite-time bounded,if there exist positive scalars α,λk,k=(1,2,···,7),positive definite matrices Pi,Q1,Q2,Q3,S1,S2,and positive diagonal matrices U1,U2with appropriate dimensions,such that the following LMI holds.

ProofThe proof is similar to that of Theorem 3.1,so it is omitted here.

3.2 Finite time H∞control

Consider the neural networks(2.1),under the controller u(t)=Kη(t)x(t),t∈ (0,Tf],the corresponding neural network is given by

Theorem 3.3Consider the neural networks(3.23)–(3.25),and letIf there exist positive scalars α,τ,σ,ρ,δ1,δ2,positive definite symmetric matrices Pi,Q1,Q2,Q3,S1,S2with appropriate dimensions and positive diagonal matrices U1,U2,such that the following inequalities hold,

where

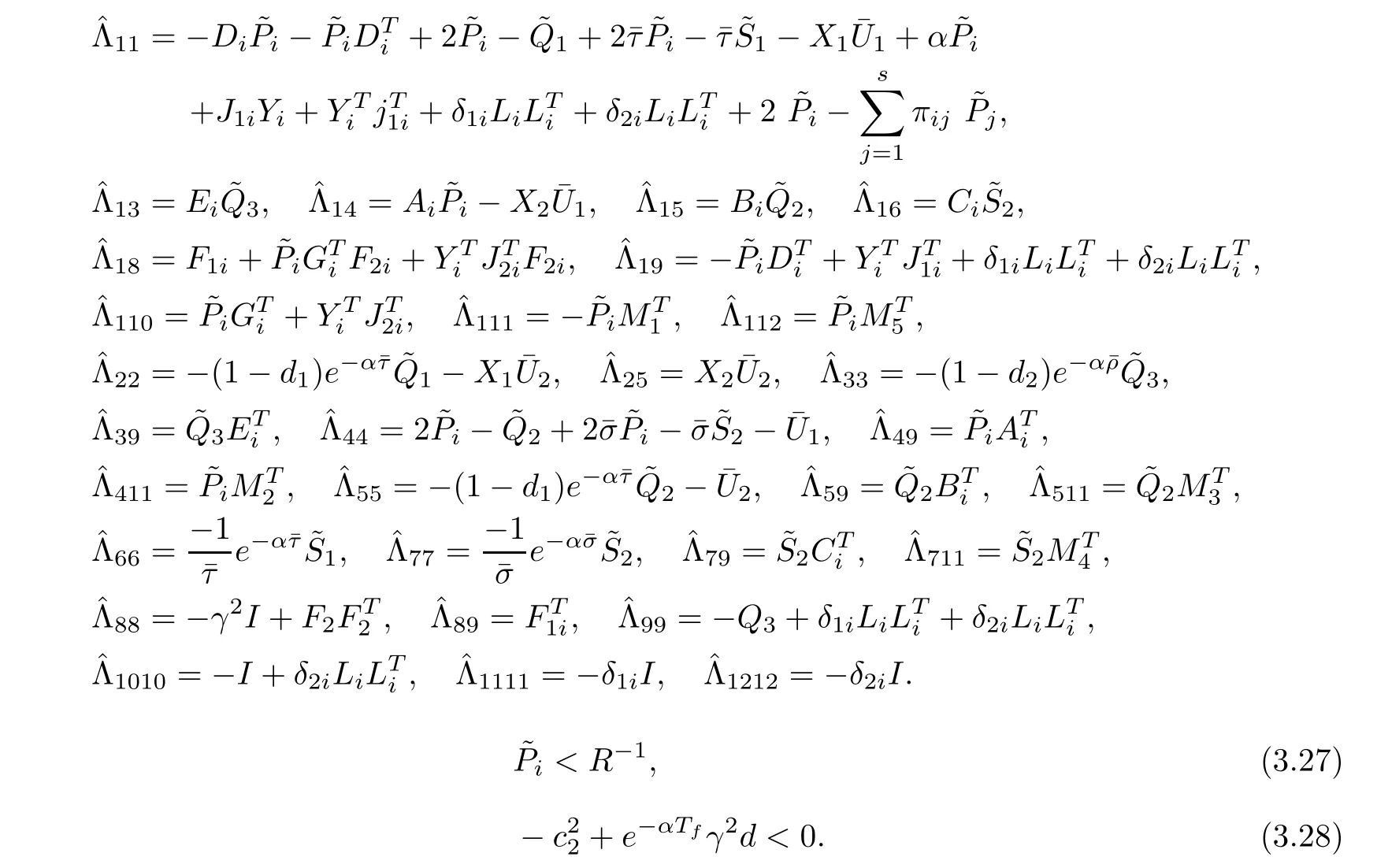
ProofReplacing Di,Ai,Bi,Ci,Giin the left side of(3.26)withJ2iKi,and using Schur complement lemma,we can obtain

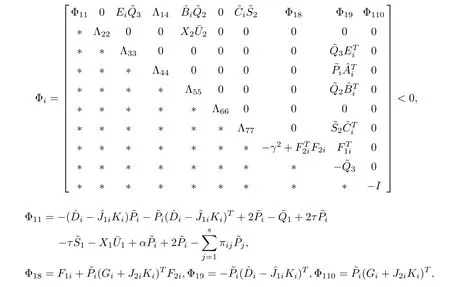
By Assumption 1,we have

with

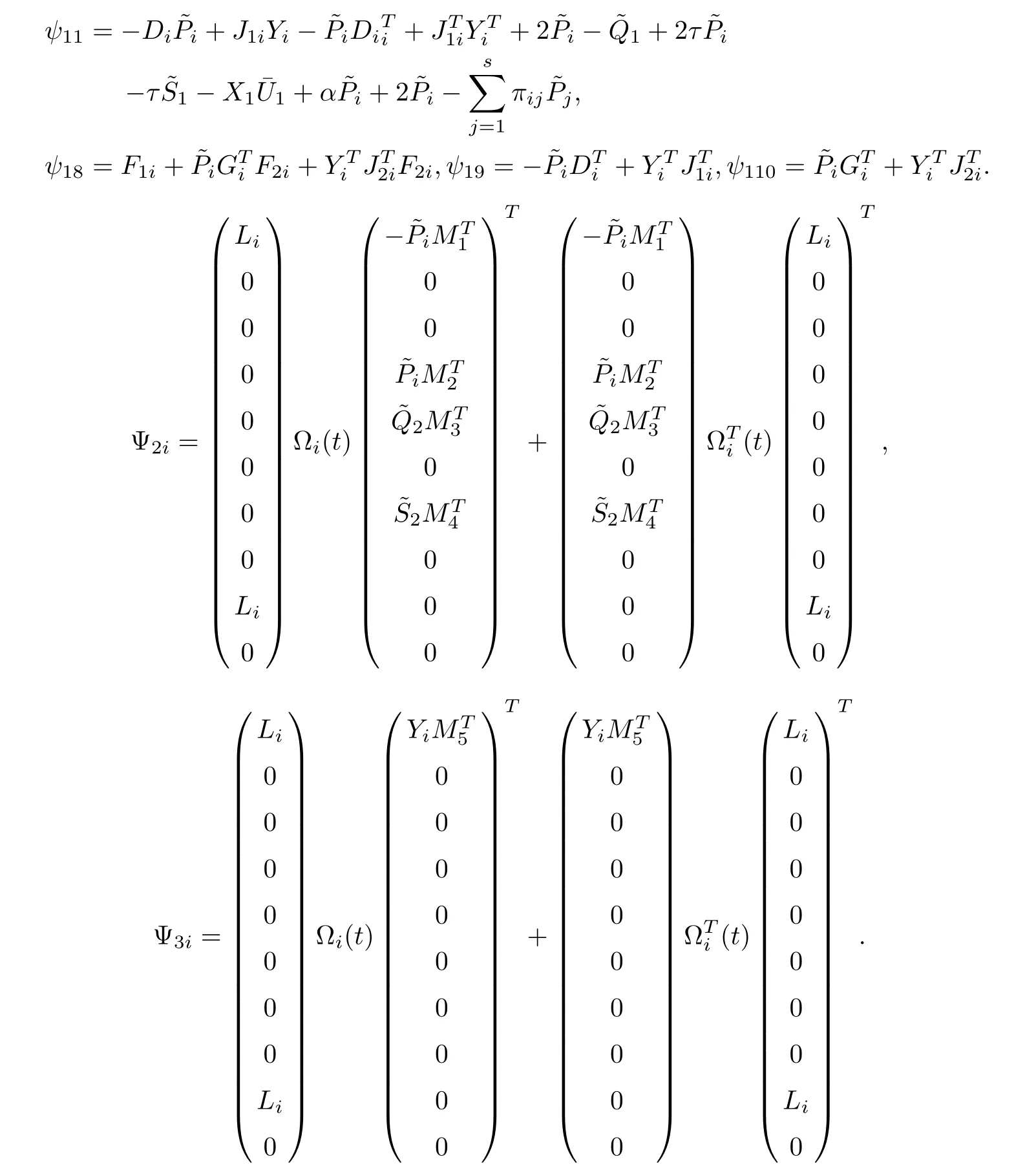
By Lemma 2.7,we can get

Using Schur complement lemma,from(3.26)we obtain Ψi＜ 0.Thus,the proof is completed.

4 Numerical Example

In this section,we present numerical examples to illustrate the effectiveness and advantage of the obtained theoretical results.

Example 1Consider neural networks(3.1)with parameters as follows

X1=diag{0,0},X2=diag{−2,2}.For the given values of Tf=0.7,τ=0.3,=0.5,d1=0.6,d2=0.4,=0.8,α=1.5,c1=0.01,d=0.2,by Theorem 3.1 we know that the optimal value ofdepends on parameter α.By solving the matrix inequalities(3.2)–(3.3),we can get the optimal bound ofwith different value of α in each subsystems.The smallest bound can be obtained as=0.4315 when α=1.5.

Example 2Consider the neural networks(2.1)with parameters as follows:

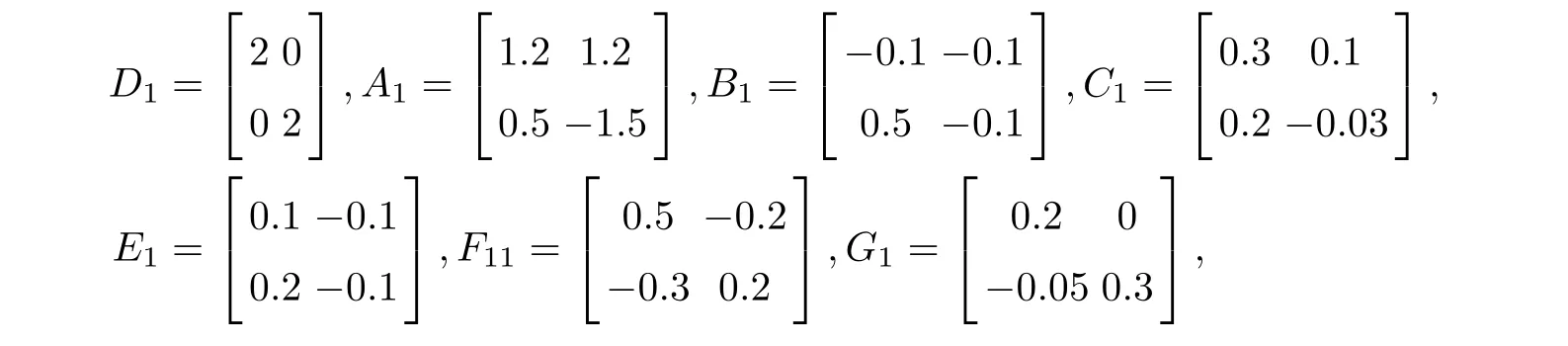
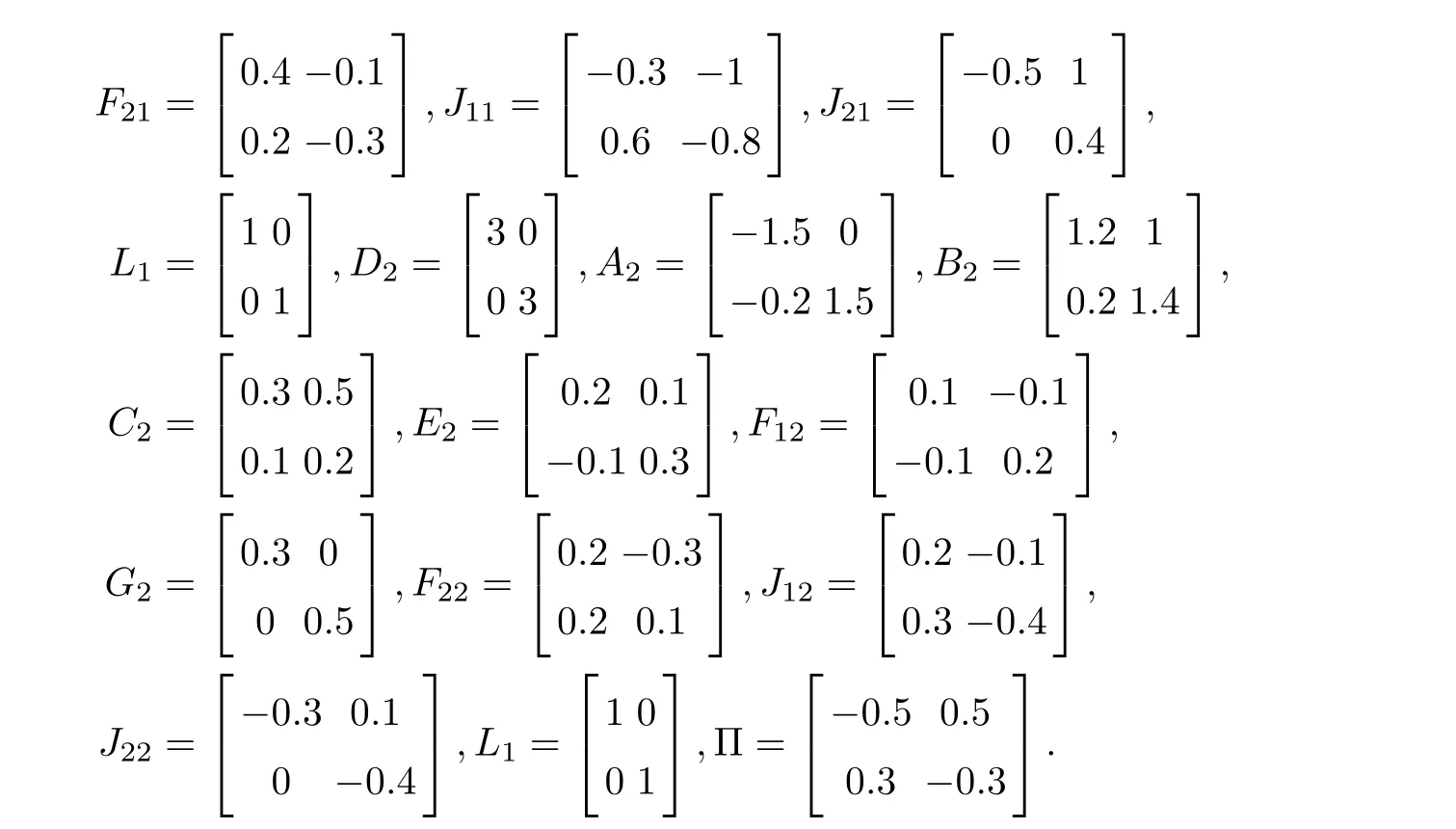
M1i=M2i=M3i=M4i=M5i=0.3I,X1=diag{0,0},X2=diag{−2,2}.For the given values of Tf=5,¯τ=0.5,¯ρ=0.2,d1=0.9,d2=0.3,¯σ=1,α=4,c2=4,d=2,µ=2,R=I and taking γ2as optimized variable with a fixed α,by solving the optimal value problem for each subsystem according to Theorem 3.4,we get the following conclusion.For subsystem 1,when α ∈ [1.618,11.512],the LMI in Theorem 3.3 has feasible solution,and γmin=0.6000.

By solving the matrix equalities in Theorem 3.3,we obtain

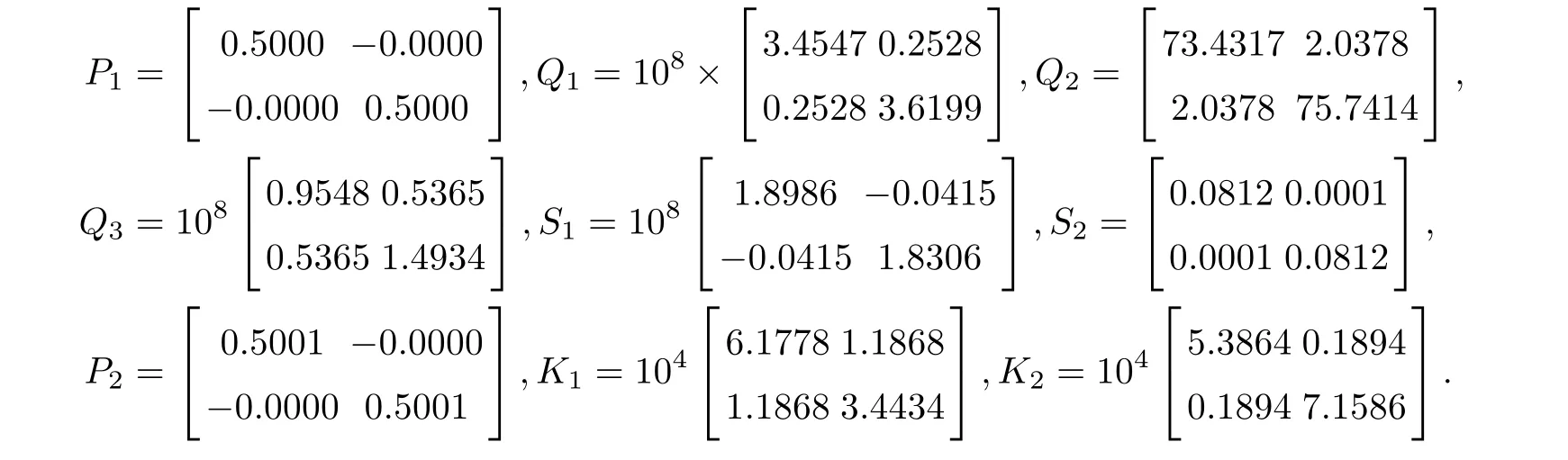
Example 3Consider the class of Markovian jumping neural networks[41]

with parameters as follows:

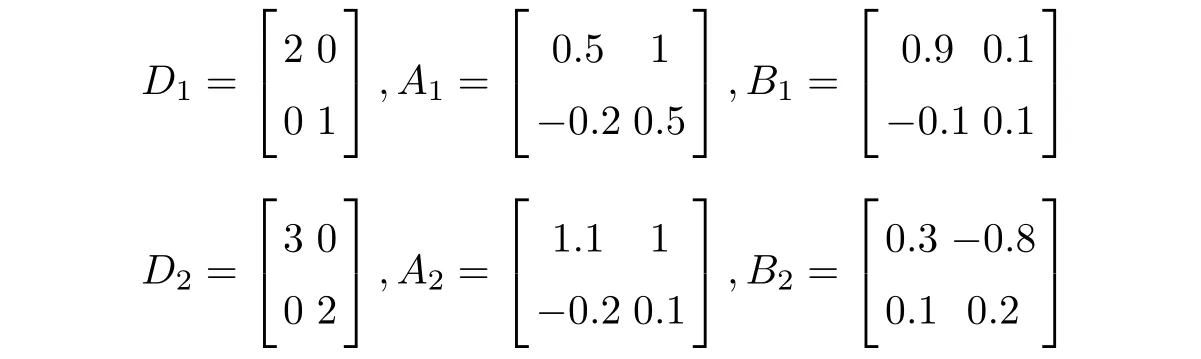
X1=diag{0,0},X2=diag{1,1}.For the given values of Tf=5,=0.26,d1=0.2,=1,c1=0.5,d=2,R=I,by solving the optimal value problem for each subsystem according to Corollary 3.2,we get the minimal value of c2=1.8101.It should be mentioned that the minimal c2in[41]is 5.4296.Thus delayed Markovian jumping neural networks is stochastically finite-time bounded with respect to(c1,c2,Tf)with minimal c2smaller than that in[41].Therefore,the stability conditions proposed in this article are less conservative than[41].

Example 4Consider the class of Markovian jumping neural networks[42],

with parameters as follows:

the activation function X1=diag{0.2,0.2,0.2},X2=diag{0.4,0.4,0.4}.For the given values of Tf=5,d1=0.2,c1=0.5,c2=0.3,d=2,R=I,by solving the problem for each subsystem according to Corollary 3.2,we get the upper bound of¯τ=4.450,whereas for the upper bound of¯τ=2.5 in[42],it shows that delayed Markovian jumping neural networks is stochastically finite-time bounded with respect to(c1,c2,T).Hence the results in this article are less conservative than that in[42].

Conclusion

In this article,we investigate the problem of robust finite-time H∞control for a class of uncertain neutral-type neural networks with distributed time varying delays.The finite-time boundedness analysis and finite-time H∞controller design for neural networks system with H∞disturbance attenuation level γ are studied.Numerical examples are provided to show the effectiveness of the proposed method.The results are compared with the existing results to show the conservativeness.

Figure 1 State trajectories of the system in Example 1

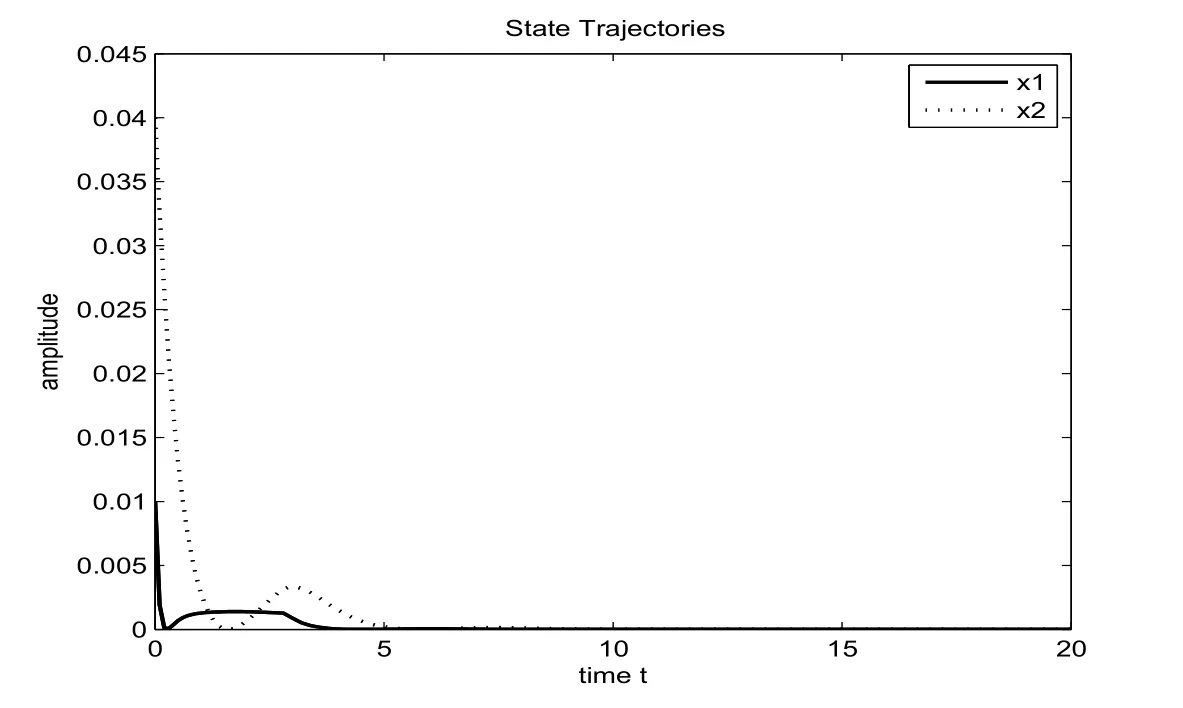
Figure 2 State trajectories of the system in Example 2

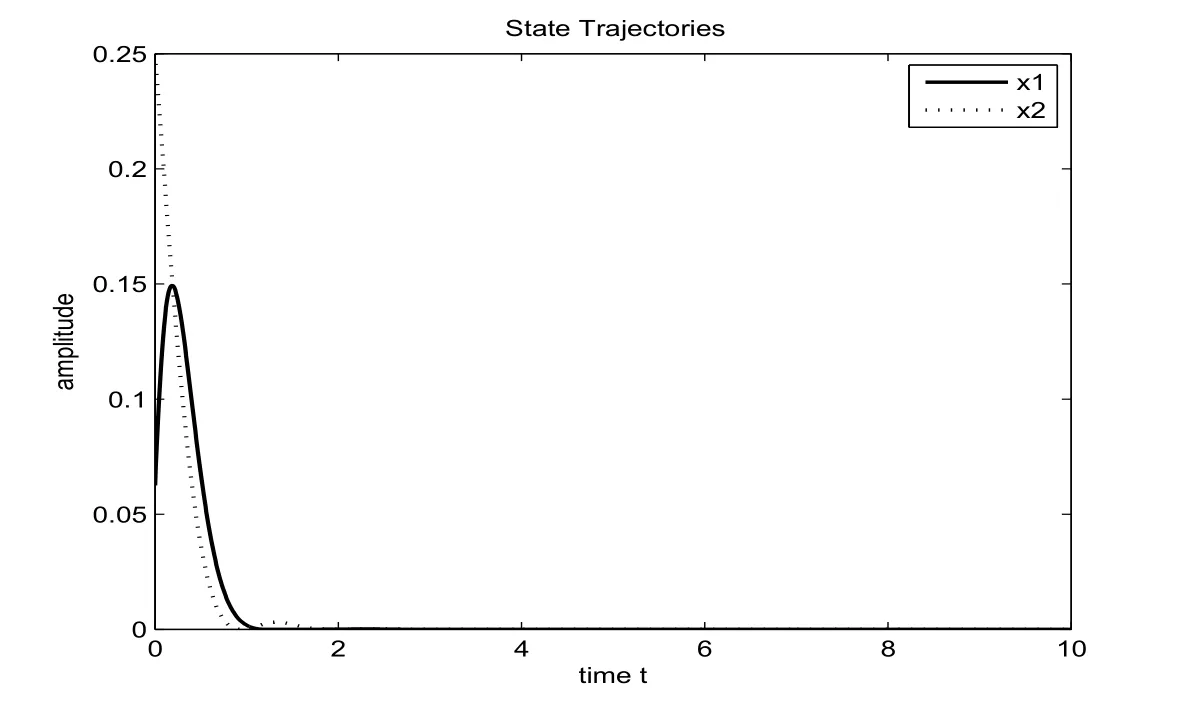
Figure 3 State trajectories of the system in Example 3

Figure 4 State trajectories of the system in Example 4

[1]Wang S,Shi T,Zeng M,et al.New results on robust finite-time boundedness of uncertain switched neural networks with time-varying delays.Neurocomputing,2015,151:522–530

[2]Syed Ali M,Balasubramaniam P.Global exponential stability of uncertain fuzzy BAM neural networks with time-varying delays.Chaos Solitons Fractals,2009,42:2191–2199

[3]Kwon O M,Park M J,Park J H,et al.Improved approaches to stability criteria for neural networks with time-varying delays.J Franklin Inst,2013,350:2710–2735

[4]Yu L,Fei S,Long F,et al.Multilayer neural networks-based direct adaptive control for switched nonlinear systems.Neurocomputing,2010,74:481–486

[5]Sun X M,Zhao J,Hill D J.Stability and L2-gain analysis for switched delay systems:A delay-dependent method.Automatica,2006,42:1769–1774

[6]Hou L,Zong G,Wu Y.Robust exponential stability analysis of discrete-time switched Hop field neural networks with time delay.Nonlinear Anal Hybrid Systems,2011,5:525–534

[7]Sathy R,Balasubramaniam P.Stability analysis of fuzzy Markovian jumping Cohen-Grossberg BAM neural networks with mixed time-varying delays.Commun Nonlinear Sci Numer Simulat,2011,16:2054–2064

[8]Yao D,Lu Q,Wu C,Chen Z.Robust finite-time state estimation of uncertain neural networks with Markovian jump parameters.Neurocomputing,2015,159:257–262

[9]Tian J,Li Y,Zhao J,Zhong S.Delay-dependent stochastic stability criteria for Markovian jumping neural networks with mode-dependent time-varying delays and partially known transition rates.Appl Math Comput,2012,218:5769–5781

[10]Tian J,Xiong W,Xu F.Improved delay-partitioning method to stability analysis for neural networks with discrete and distributed time-varying delays.Appl Math Comput,2014,233:152–164

[11]Tian J,Liu Y.Improved Delay-Dependent Stability Analysis for Neural Networks with Interval Time-Varying Delays.Math Probl Eng 2015,Article ID 705367,10 pages

[12]Ren Z,Tian J.Improved stability analysis for neural networks with interval time-varying delays.Appl Mech Mater,2014,687-691:2078–2082

[13]Syed Ali M.Stability of Markovian jumping recurrent neural networks with discrete and distributed timevarying delays.Neurocomputing,2015,149:1280–1285

[14]Chen J,Wu I,Lien C,et al.Robust exponential stability for uncertain discrete-time switched systems with interval time-varying delay through a switching signal.J Appl Research Tec,2014,12:1187–1197

[15]Zeng H B,Park J H,Zhang C F,Wang W.Stability and dissipativity analysis of static neural networks with interval time-varying delay.J Franklin Inst,2015,352:1284–1295

[16]Wu X,Tang Y,Zhang W.Stability analysis of switched stochastic neural networks with time-varying delays.Neural Networks,2014,51:39–49

[17]Lian C,Zeng Z,Yao W,Tang H.Multiple neural networks switched prediction for landslide displacement.Engineering Geology,2015,186:91–99

[18]Balasubramaniam P,Syed Ali M,Arik S.Global asymptotic stability of stochastic fuzzy cellular neural networks with multiple time-varying delays.Expert Syst Appl,2015,37:7737–7744

[19]Shi K,Zhu H,Zhong S,et al.New stability analysis for neutral type neural networks with discrete and distributed delays using a multiple integral approach.J Franklin Inst,2015,352:155–176

[20]Liu D,Zhong S,Liu X,Huang Y.Stability analysis for uncertain switched neutral systems with discrete time-varying delay:a delay-dependent method.Math Comput Simulat,2009,80:828–839

[21]Xiang M,Xiang Z.Stability,L1-gain and control synthesis for positive switched systems with time-varying delay.Nonlinear Anal Hybrid Systems,2013,9:9–17

[22]Sun X,Liu G,Wang W,Rees D.Stability analysis for networked control systems based on average dwell time metheod.Internat J Robust Nonlin Cont,2010,20:1774–1784

[23]Branicky M S.Multiple Lyapunov functions and other analysis tool for switched and hybrid systems.IEEE Trans Automat Control,1998,43:475–482

[24]Feng W,Yang S X,Wu H.On robust stability of uncertain stochastic neural networks with distributed and interval time-varying delays.Chaos Solitons Fractals,2009,42:2095–2104

[25]Lee S M,Kwon O M,Park J H.A novel delay-dependent criterion for delayed neural networks of neutral type.Phys Lett A,2010,374:1843–1848

[26]Zhang Y,Shi P,Nguang S K,Zhang J,Karimi H R.Finite-time boundedness for uncertain discrete neural networks with time-delays and Markovian jumps.Neurocomputing,2014,140:1–7

[27]Liberzon D,Morse A S.Basic problems in stability and design of switched systems.IEEE Control Syst Mag,1999,19:59–70

[28]Sun Y,Wang L,Xie G.Delay dependent robut stability and H∞control for uncertain discrete-time switched systems with mode-dependent time delays.Appl Math Comput,2007,187:1228–1237

[29]Syed Ali M,Saravanakumar R.Novel delay-dependent robust H∞control of uncertain systems with distributed time-varying delays.Appl Math Comput,2014,249:510–520

[30]Lien C H,Yu K W.Non-fragle H∞control for uncertain neutral systems with time-varying delays via the LMI optimization approach.IEEE Trans Syst Man Cybernet,2007,37(Part B):493–509

[31]Liu X.Stabilization of switched linear systems with mode-dependent time-varying delays.Appl Math Comput,2010,216:2581–2586

[32]Zhang H,Dong M,Wang Y,Zhang N.Stochastic stability analysis of neutraltype impulsive neural networks with mixed time-varying delays and Markovian jumping.Neurocomputing,2010,73:2689–2695

[33]Xianga Z,Suna Y N,Mahmoud M S.Robust finite-time H∞control for a class of uncertain switched neutral systems.Commun Nonlinear Sci Numer Simul,2012,17:1766–1778

[34]Hong Y,Hong J,Xu Y.On an output feedback finite time stabilization problem.IEEE Trans Automat Control,2001,46:305–309

[35]Xiang W,Xiao J.H∞finite-time control for swiched nonlinear discrete-time systems with norm-bounded disturbance.J Franklin Inst,2011,348:331–352

[36]Zhang W,Fang J,Cui W.Exponential stability of switched genetic regulatory networks with both stable and unstable subsystems.J Franklin Inst,2013,350:2322–2333

[37]Lin X,Du H,Li S.Finite-time boundedness and L2-gain analysis for switched delay systems with normbounded disturbance.Appl Math Comput,2014,217:5982–5993

[38]Wang T,Tong S.H∞control design for discrete-time switched fuzzy systems.Neurocomputing,2015,14:782–789

[39]Li X,Lin X,Li S,Zou Y.Finite-time stability of switched nonlinear systems with finite-time unstable subsystems.J Franklin Inst,352:1192–1214

[40]Song Q,Wang Z.New results on passivity analysis of uncertain neural networks with time-varying delays.Int J Comput Math,2015,87:668–678

[41]He S,Liu F.Finite-time boundedness of uncertain time-delayed neural network with Markovian jumping parameters.Neurocomputing,2013,103:87–92

[42]Wang T,Zhao S,Zhou W,Yu W.Finite-time state estimation for delayed Hop field neural networks with Markovian jump.ISA Transactions,2015,57:43–50