TWO DIMENSIONAL MELLIN TRANSFORM IN QUANTUM CALCULUS∗

Kamel BRAHIM Latifa RIAHI

Faculty of Sciences of Tunis.University of Tunis El Manar,Tunisia

E-mail:Kamel.Brahim@ipeit.rnu.tn;riahilatifa2013@gmail.com

1 Introduction

It is well known that the integral transforms are very important in the areas of science and engineering,and they attracted the attention of many researchers(see[1–5]).Two of the most frequently used formulas in the area of integral transforms are the classical Mellin transform and the corresponding formal inversion formula;they were successfully applied in the theory of differential equations,plain harmonic problems in special domains,elasticity mechanics,special functions,summing series,and calculating integrals.

In 1854–1933,Hjalmar Mellin defined the Mellin transform of a suitable function f over(0,∞)as

In 2006,A.Fitouhi et al[5]studied the q-analogue of the Mellin transform and its inversion given,respectively,by

and

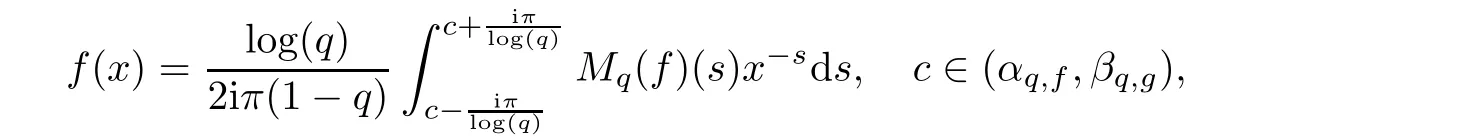
where Rq,+:={qn,n∈Z}.

As a generalization of the Mellin transform,the two-dimensional Mellin transform is defined by[2,13]

the inversion formula for the two-dimensional Mellin transform is given by the following relation

The two-dimensional Mellin convolution product of the functions f and g is defined by

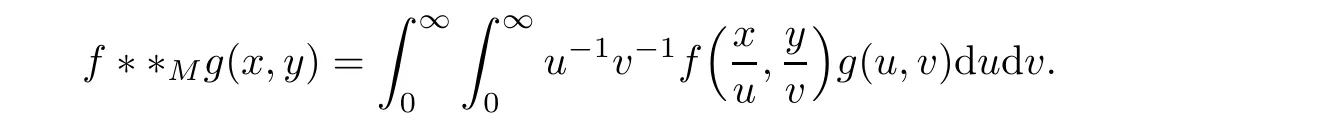
In[8],using two parameters of deformation q1and q2,Haran et al gave the definition of an analogue of the two-dimensional Mellin transform by

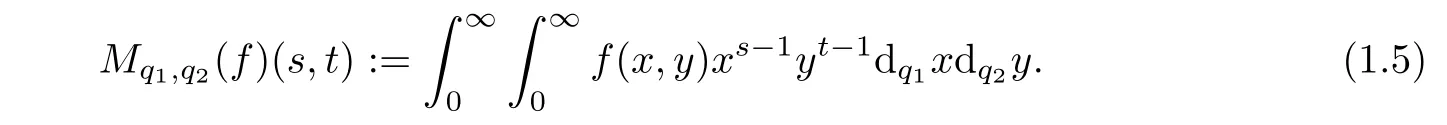
The aim of this article is devoted first to study the analogue of the Mellin transform Mq1,q2(f)(1.5)and second to discuss its properties and to give its inversion formula which is an analogue of(1.4).Furthermore,we define the convolution product.And finally as applications,we prove an analogue of the Titchmarsch theorem.

This article is organized as follows:In Section 2,we present some preliminary results and notations that will be useful in the sequel.In Section 3,we introduce the˜q-analogue of the two-dimensional Mellin transform,give some properties,and prove the inversion formula of the ˜q-two dimensional Mellin transform.In Section 4,we study the convolution product and give some relations of the˜q-analogue of the two-dimensional Mellin transform.In Section 5,we give some applications.Finally,in Section 6,we establish Paley-Wiener theorems for the modified-two-dimentional Mellin transform.

2 Basic Definitions

For the convenience of the reader,in this section we provide a summary of the mathematical notations and definitions used in this article(see[6,9,10]).

For q∈(0,1)and a∈C,the q-shifted factorials are defined by

We also denote

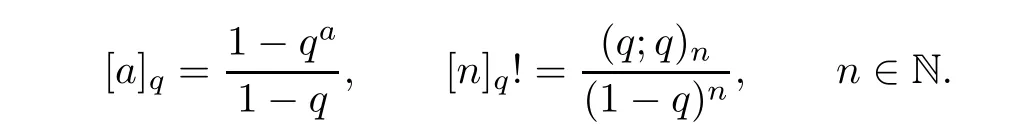
The q-derivatives Dqf andof a function f are given by[10]:

(Dqf)(0)=f′(0)andprovided f′(0)exists.

If f is differentiable,then(Dqf)(x)andtend to f′(x)as q tends to 1.For n ∈ N,we note

The q-derivative of a product

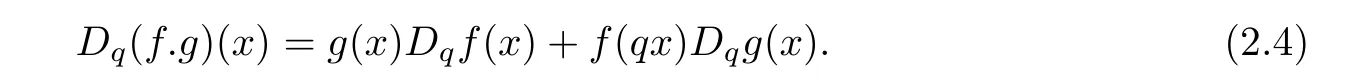
The q-Jackson integrals from 0 to a and from 0 to∞are defined by[9]

provided the sums converge absolutely.

A q-analogue of the integration by parts formula is given by

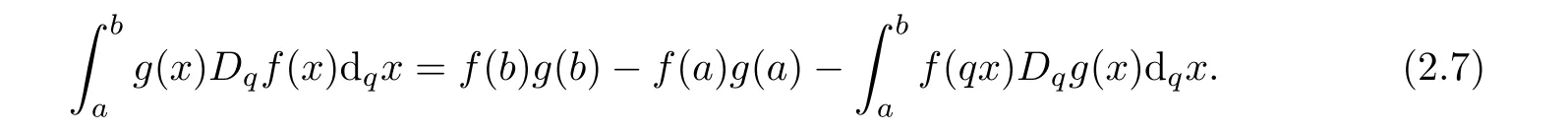
Use the q-Jackson integrals from 0 to∞to define the double integrals for q1,q2∈(0,1)by

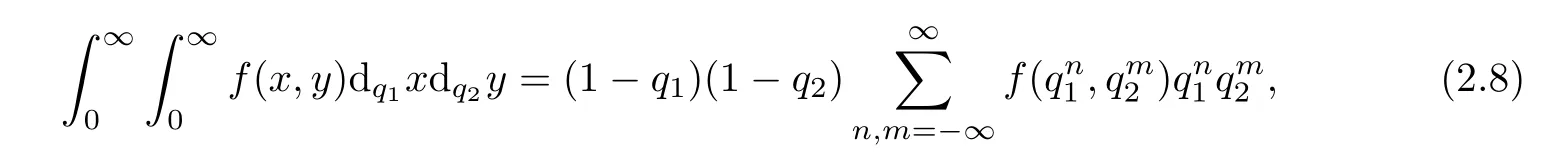
provided the sums converge absolutely.

The q-analogues of the exponential function are defined by(see[6,15])

and the q-exponential functions are q-analogues of the classical one and satisfy the relations

and

Jackson defined the q-analogue of the classical gamma functionby(see[17–25])

It is well known that it satisfies

The function Γqhas the following q-integral representations

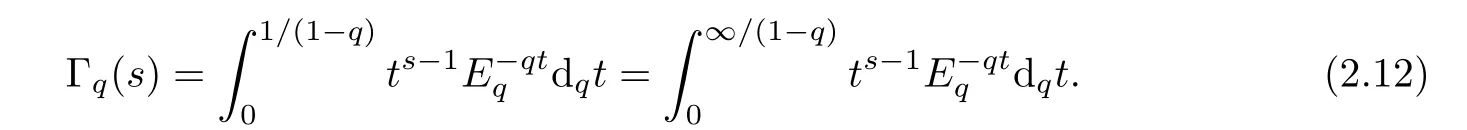
In[15],Sole A.De and Kac V.G.gave a q-integral representation of Γqbased on the exponential functionand gave a q-integral representation of q-Beta function as follows:

For∀s,t＞ 0,we have

and

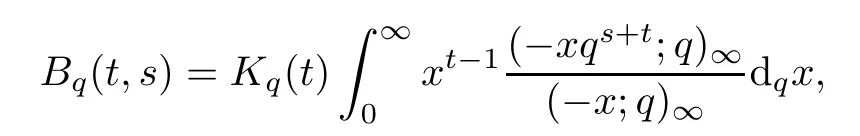
Where log(x)means loge(x).

Definition 3.1Letand f be a function defined on Rq1,+×Rq2,+.Then,the-two dimensional Mellin transform of f is defined by

Remark 3.2It is easy to see that for a suitable function f,M˜q(f)(s,t)tends to M(f)(s,t)whentend to(1,1).

We define the set Hfby

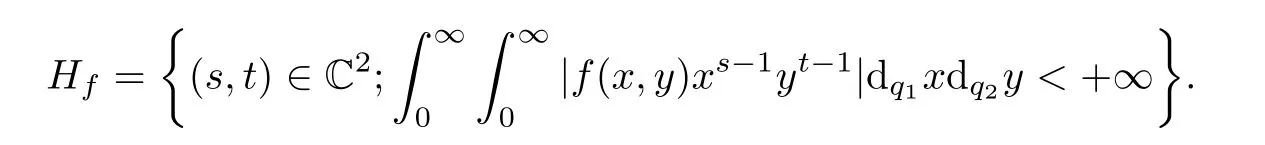
Proposition 3.3If f is a function defined on Rq1,+×Rq2,+,then M˜q(f)is analytic on Hfand we have the followings:

(1) ∀(s,t)∈C2,M˜q(f)(s,t)=M˜q[ilog(x)f(x,y)](s,t);

(2) ∀(s,t)∈C2,M˜q(f)(s,t)=M˜q[ilog(y)f(x,y)](s,t);

(3) ∀(s,t)∈C2,M˜q(f)(s,t)=M˜q[−log(x)log(y)f(x,y)](s,t).

3.1 Properties

In the following subsection,we give some interesting properties of the˜q-two dimensional Mellin transform,which coincide with the classical ones whentend to(1,1).

(P1)For a∈Rq1,+,b∈Rq2,+and(s,t)∈C2,we have

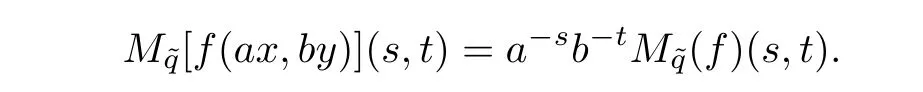
(P2)For(s,t)∈ C2such that(−s,−t)∈ Hf,we have

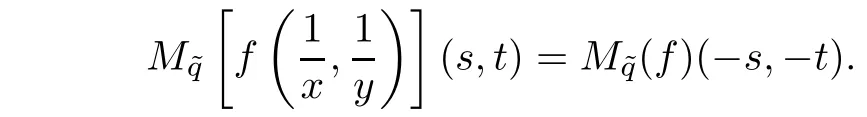
(P3)For(s,t)∈ C2such that(−s,t)∈ Hf,we have

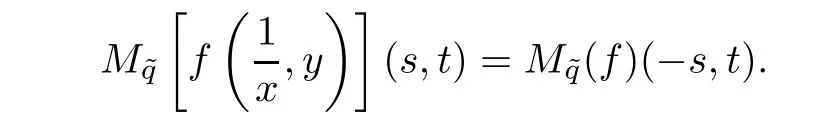
(P4)For a,b∈R and(s,t)∈C2such that(s+a,t+b)∈Hf,we have

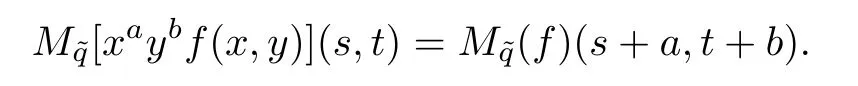
(P5)For(s,t)∈C2such that(s−1,t)∈Hf,we have

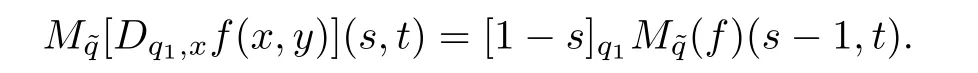
(P6)For(s,t)∈C2such that(s,t−1)∈ Hf,we have

(P7)For(s,t)∈C2such that(s−1,t−1)∈Hf,we have

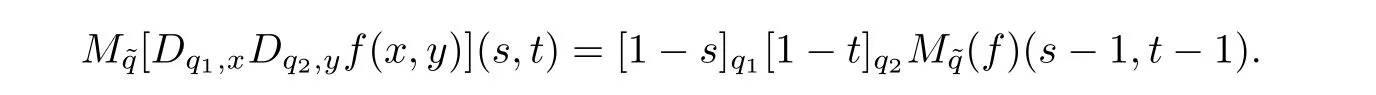
By induction,it is obtained that:for n,m∈N∗and(s,t)∈C2such that(s−n,t−m)∈Hf,

(P8)For(s,t)∈C2such that(s−1,t)∈Hf,we have

(P9)For(s,t)∈C2such that(s,t−1)∈ Hf,we have

(P10)For(s,t)∈C2such that(s+1,t)∈Hf,we have

(P11)For(s,t)∈C2such that(s,t+1)∈Hf,we have

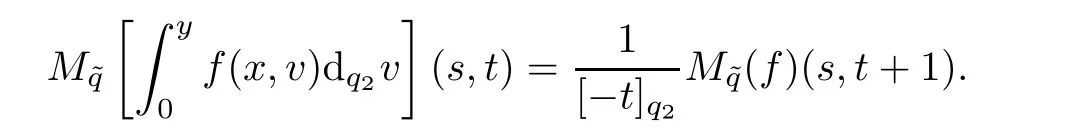
(P12)For τ＞0,ρ ＞0 and(s,t)∈C2such that∈Hf,we have

(P13)Let(µk)kand(νk)kbe two sequences of Rq1,+× Rq2,+,let(λk)kbe a sequence of C,and let f be a suitable function,then we have

provided the sums converge.

The proof of all previous properties are easily established by using the definition of the ˜q-two dimensional Mellin transform and the properties of the q-Jackson integrals mentioned before.

Example 3.4Let q1=q2=q, s=n,and t=m such that n,m∈N∗and the functionSuppose thatthen by formulas(2.11),(2.7),and(2.13),we have

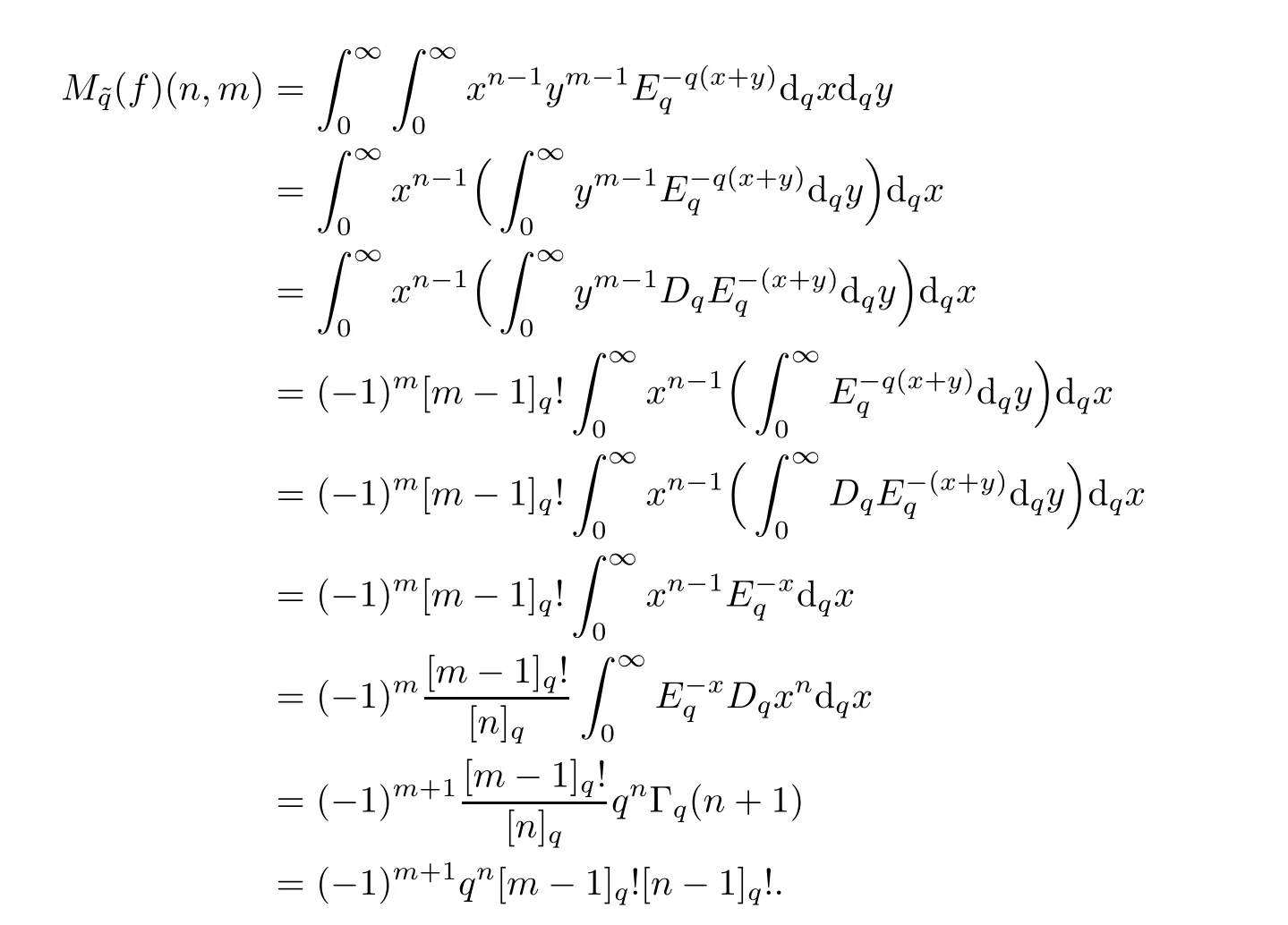
Theorem 3.5Let f be a function defined on Rq1,+×Rq2,+and let(c1,c2)∈Hf∩R2,then for all(x,y)∈Rq1,+×Rq2,+,we have

ProofBy definition,we have

Multiplying the both sides of(3.3)byand integrating with respect to t fromtowe get

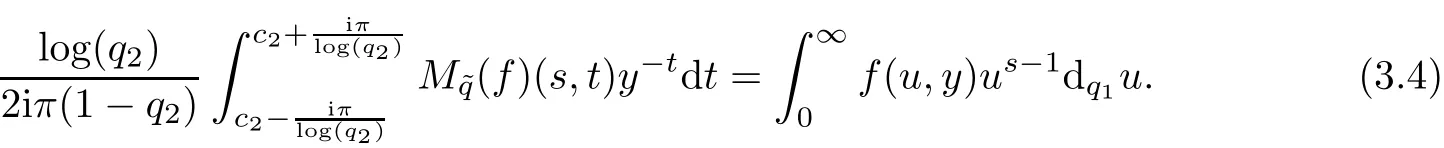
Now,multiplying the both sides of(3.4)bythen integrating the resulting identity with respect to s fromthe result follows.

Definition 4.1The-two dimensional Mellin convolution of the functions f and g is the function f∗M˜qg defined by

provided the double integral exists.

Using classical arguments,one can easily prove the following result.

Proposition 4.2If the-two dimensional Mellin convolution product of f and g exists,then

Proposition 4.3For a suitable functions f and g,the following relations holds:

and

Proof(1)From relation(4.3)and the inversion formula,we have,for x=1 and y=1,

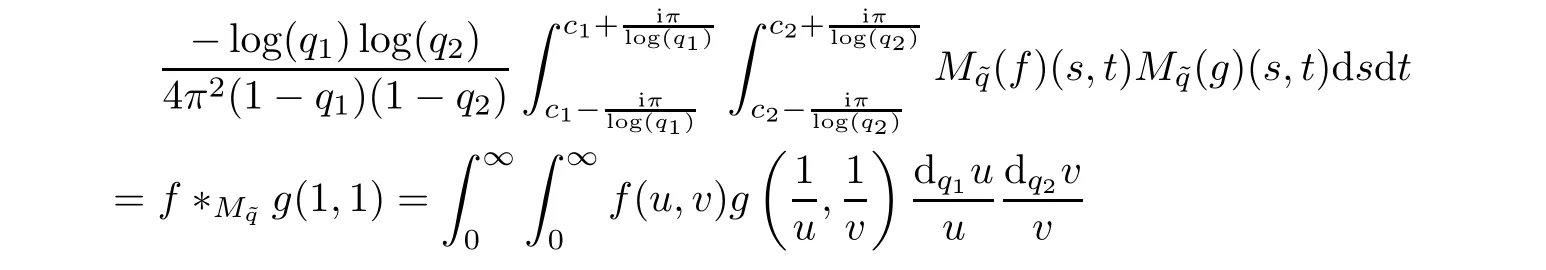
5 Applications

Application 5.1-double integral equations

Lemma 5.1Let k and g be a pair functions defined on Rq1,+×Rq2,+such that the set Ik,g=Hk∩{(1−s,1−t),(s,t)∈Hg}is not empty.Put

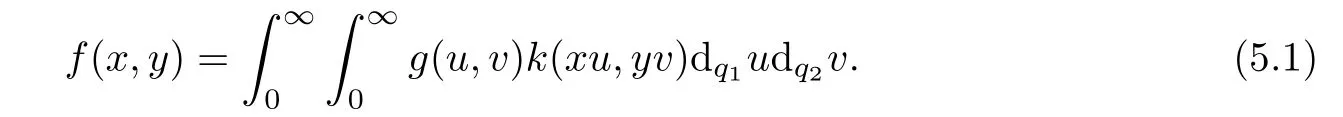
Then,

ProofWe have

and we make the change of variable:xu=z and yv=w,then,we obtain

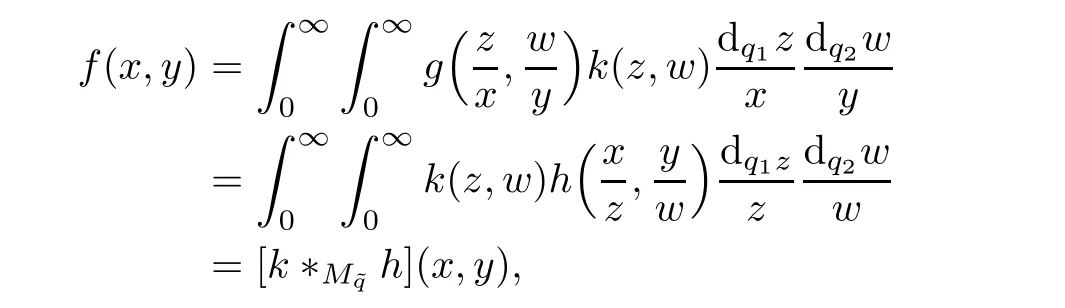
Theorem 5.2Let k and g be two functions defined on Rq1,+×Rq2,+.For a suitable reals c1and c2,put for all(x,y)∈Rq1,+×Rq2,+,

and suppose that the set IL,g=HL∩{(1−s,1−t),(s,t)∈Hg}is not empty.Then,the following integral equation:

has the solution

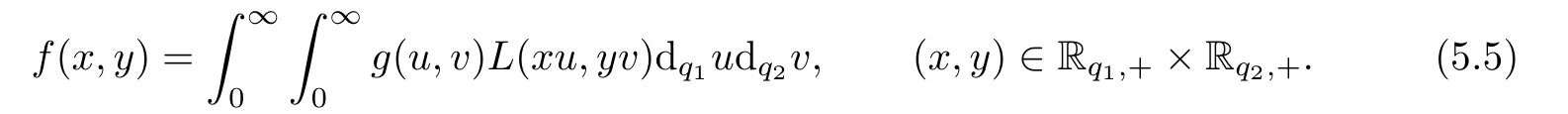
Furthermore,if

equation(5.4)has the solution

ProofFrom formula(5.4),we get

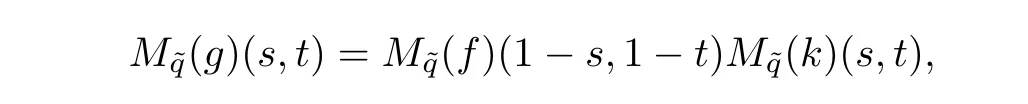
then,

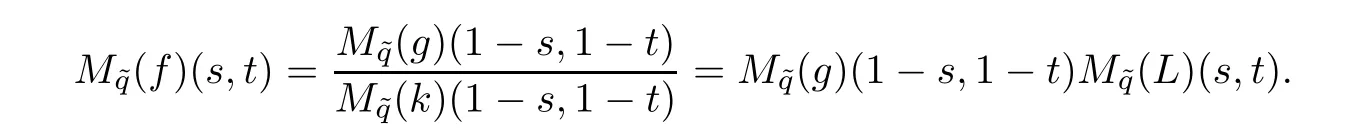
By(3.2),we obtain

Application 5.2Analogue of the Titchmarsh Theorem.

Theorem 5.3Let k be a function defined on Rq1,+×Rq2,+such that the set Hkis not empty.If the integral equation

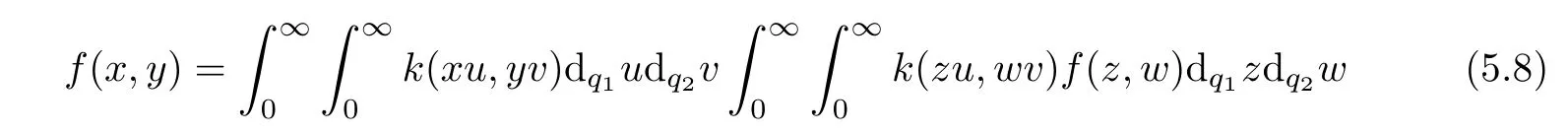
has a suitable solution f,then,for every s,t∈C such that(s,t)and(1−s,1−t)∈Hk,we have

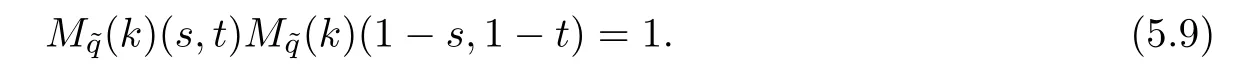
ProofThe integral equation(5.8)may be written as a pair of reciprocal formulas:

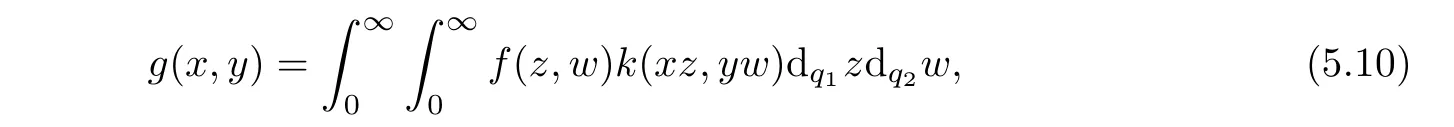
and

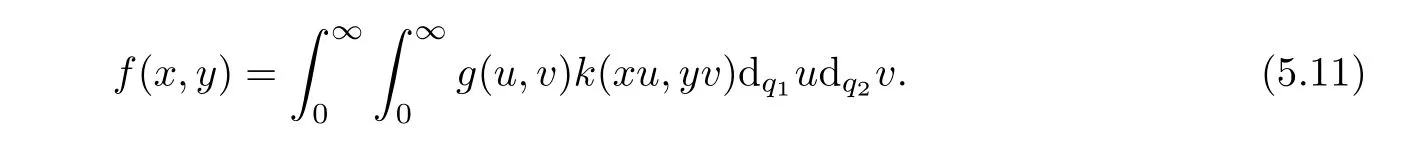
Using Lemma 5.1,we obtain

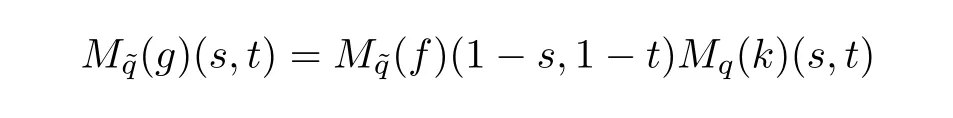
and

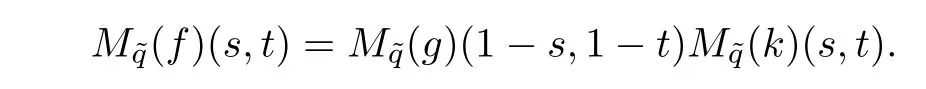
Changing s into 1−s and t into 1−t in one of these equations and multiplying,we deduce that

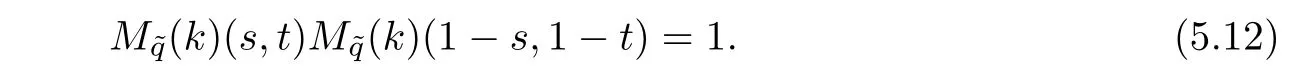
6Paley-Wiener Thoeremes for the Modified-two Dimentional Mellin Transform

Definition 6.1Let f be a function defined on Rq1,+×Rq2,+,we define the modified-double Mellin transformof f as

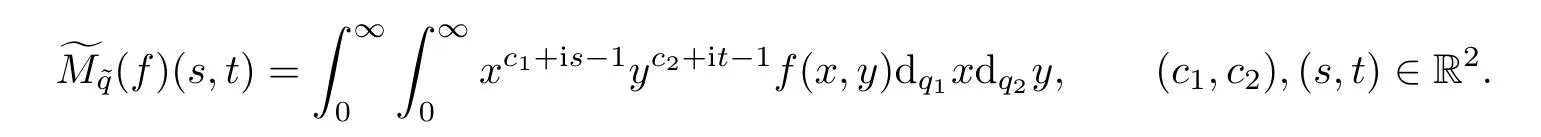
Proposition 6.2Let f be a function defined on Rq1,+×Rq2,+,the modified˜q-double Mellin transformof f is aperiodic function.

ProofUsing(2.8),we have

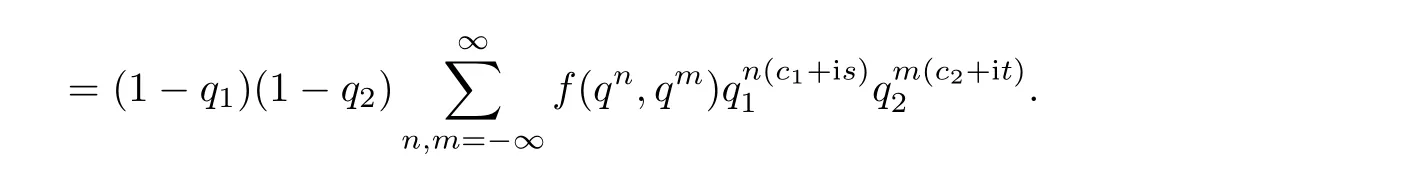
For all n,m∈N,we have

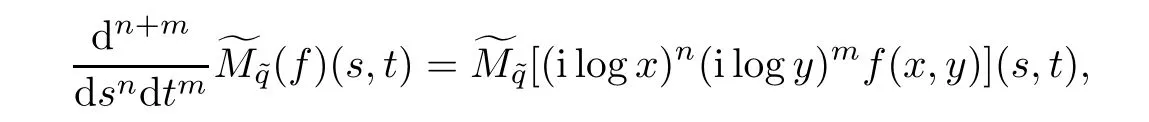
then for a polynomial function P(·,·),we have

We consider

and

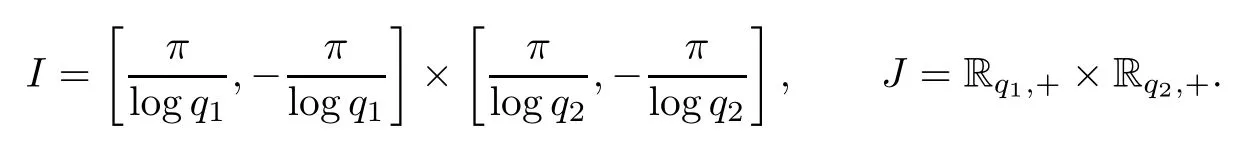
and

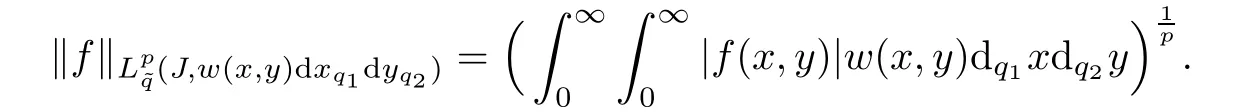
Theorem 6.3Let f be a function defined on J such thatThen,∈L∞(I,dsdt)and

ProofFor all(s,t)∈I,we have

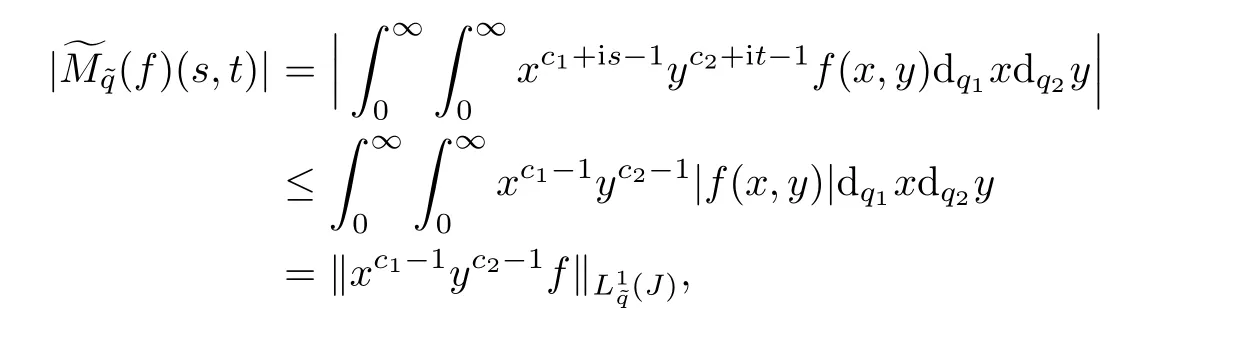
then

Theorem 6.4(Plancherel formula) Let f be a function on J such thatThen,M˜q(f)∈L2(I,dsdt)and

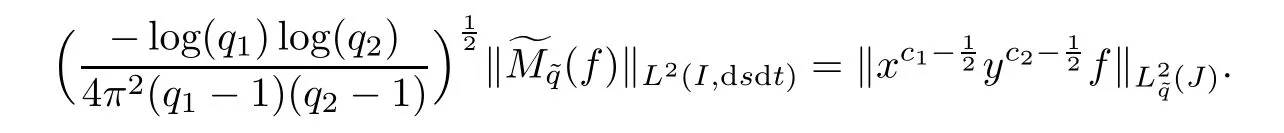
ProofUsing(4.5)and(P4),we have

Thus,

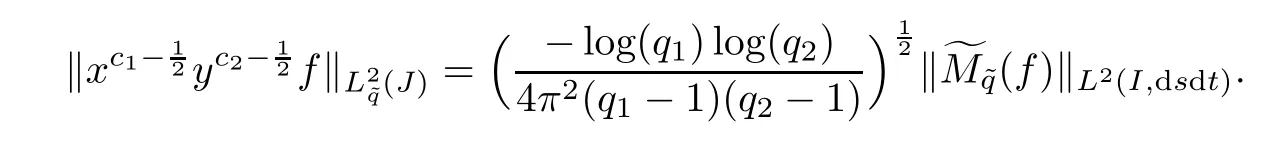
Theorem 6.5(Hausdorff-Young inequality) Let f be a function defined on J and 1 ≤n≤2(resp.n=1)such thatThen,for m=(resp.m=∞),we have∈Lm(I,dsdt)and

ProofLet T be the linear operator defined by T(f)=From Theorem 6.3,we have,for all

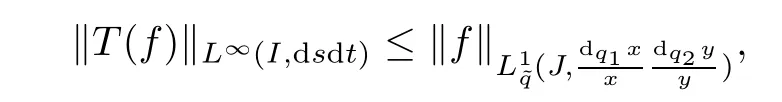
and from Theorem 6.4,we have,for all

then,from the Riesz-Thorin interpolation theorem(see[14]),we have

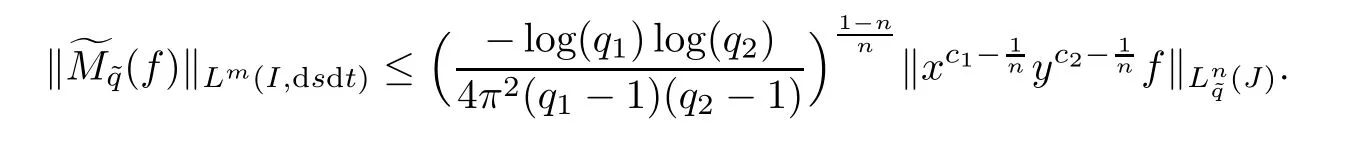
We begin by the following useful Lemma.

Lemma 6.6Let p＞0,and F and Q be two functions defined on J,such that QnF∈for all n=0,1,2,···,then

ProofThe case F=0 is trivial.Suppose now that F/=0 and we define the measureµon J by

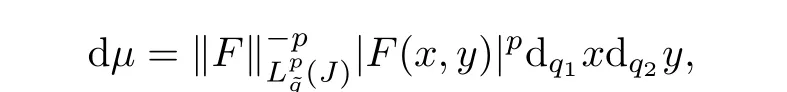
then,we haveµ(J)=1 and

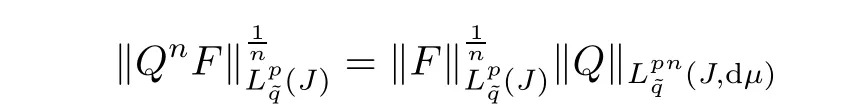
On the other hand,we have

and

Then,we obtain

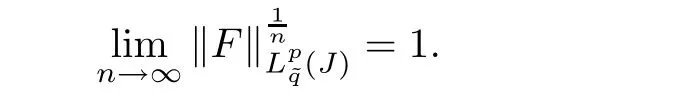
Thus,Lemma 6.6 is proved.

Theorem 6.7Let f be a function defined on J such that

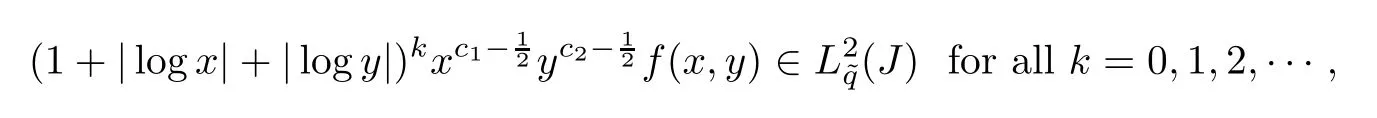
then

In particular,supp(f)∩J⊂Ω,if and only if

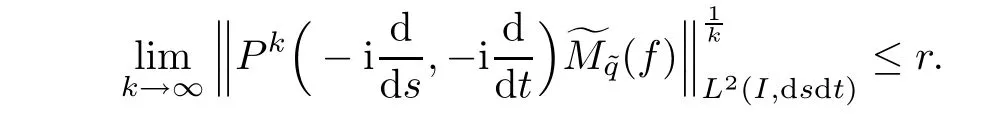
ProofBy relation(6.1)and the Plancherel formula,we have

On the other side,Lemma 6.6 gives

Then,the fact that supp(f)∩J⊂Ω shows that

and the result follows.

We can show easily a particular case for

Owing to the Hausdorff-Young inequality,the previous theorem can be generalized by the substitution of the L2norm by an Lpnorm,2≤p≤∞.This is the aim of the following result.

Theorem 6.8Let 2≤ p≤ ∞ and P be a polynomial function with real coefficients,satisfying

ProofFor 2 ≤ p ≤ ∞,we note p′,its conjugate number(that is,+=1).If 2≤ p＜ ∞,then from the Hausdorff-Young inequality and relation(6.1),we have

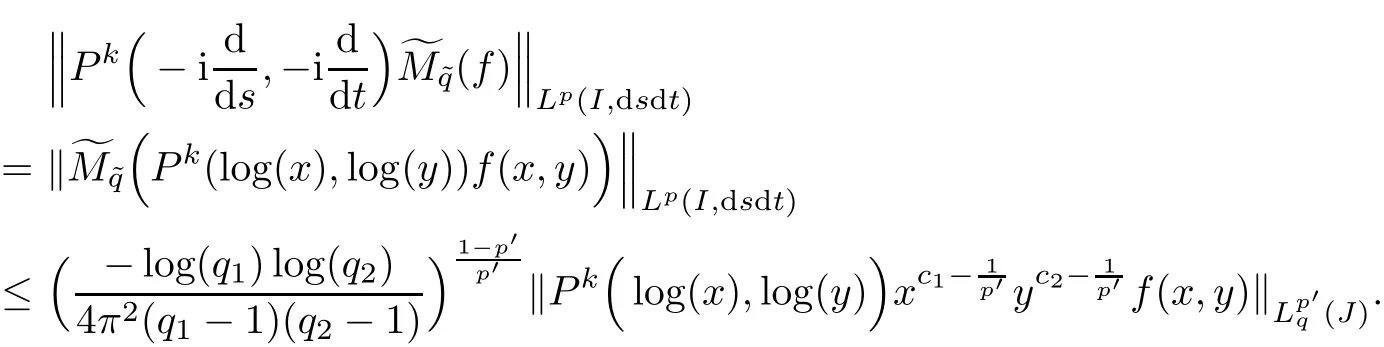
So,by Lemma 6.6,we get

Now,if p= ∞,from Theorem 6.3 and by the q-Hölder inequality(see[12]),we obtain

Consequently,

As well,the use of Lemma 6.6 gives

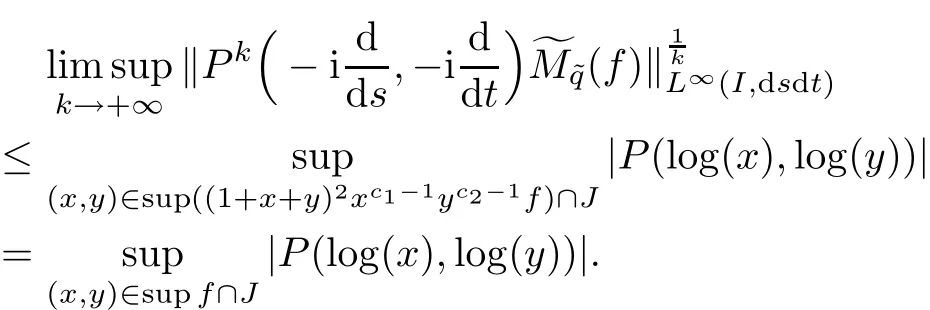
So,by the q-Hölder inequality(see[12]),we obtain

And,from Theorem 6.7,we obtain

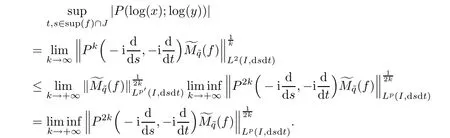
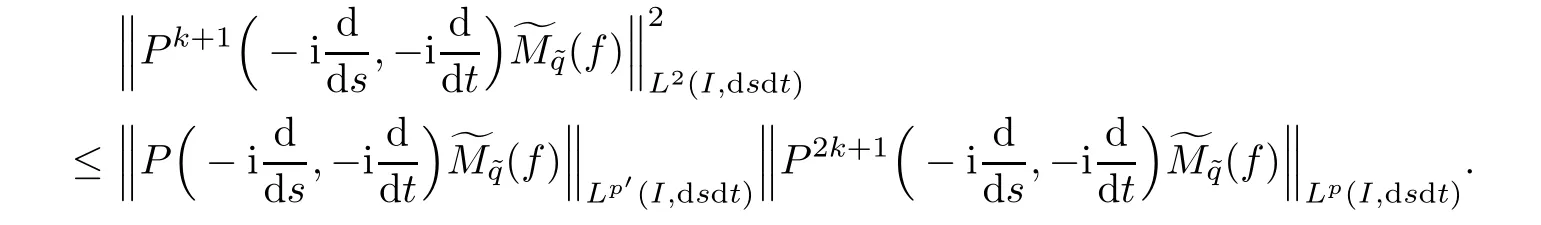
Therefore,

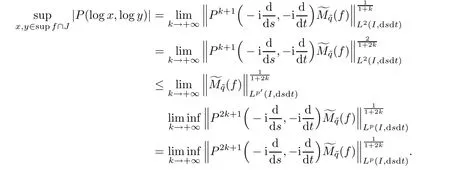
Finally,the result follows from this relation and formulas(6.2)and(6.3).

[1]Bertrand,Jacqueline,Bertrand P,Ovarlez J P.The Mellin Transform//Alexander Poularikas.Transforms and Applications Handbook.Boca Raton,Florida:CRC Press,1996

[2]Brychkov Yu A,Glaeske H J,Prudnikov A P,Vu Kim Tuan.Multidimensional Integral Transformations.Gordon Breach Science Publishers,New York-Reading,1992

[3]Davies B.Integral Transforms And Their Applications.2nd Edition.New York,NY:Springer-Verlag,1984

[4]Eltayeb H,Kih¸cman A.A Note On Mellin Transform And Partial Differential Equations.Inter J Pure Appl Math,2007,34(7):457–467

[5]Fitouhi A,Bettaibi N,Brahim K.The Mellin Transform In Quantum Calculus.Constructive Approximation,2006,23(3):305–323

[6]Gasper G,Rahmen M.Basic Hypergeometric Series.2nd Edition.Eencyclopedia of Mathematis and its Applications,96.Cambridge University Press,2004

[7]Grafakos L.Classical and Modern Fourier Analysis.New Jersey:Pearson Education,Inc,2004

[8]Haban S,Kurokawa N,Wakayama M.Jackson-Mellin’s Transform Of Modular Forms And q-Zeta Functions.Kyushu J Math,2007,61:551–563

[9]Jackson F H.On a q-Definite Integral.Quart J Pure Appl Math,1910,41:193–203

[10]Kac V G,Cheung P.Quantum Calculus,Universitext.New York:Springer-Verlag,2002

[11]Koornwinder T H.Special Functions And q-Commuting Variables//Special Functions,q-Series and Related Topics.The Fields Institute Communications Series,American Mathematical Society,1997:131–166.arXiv:q-alg/9608008

[12]Krasniqi V,Mansour T,Shabani A.Some inequalities for q-polygamma function and ζq-Riemann zeta functions.Annales Mathematicae et Informaticae,2010,37:95–100

[13]Kropivsky P L,Ben-Naim E.Scaling And Multiscaling In Models Of Fragmentation.American Physical Society,1994,50(5):363–375

[14]Sadosky C.Interpolation of Operators and Singular Integrals//Monographs and textbooks in pure and applied mathematic,53.New York:Marcel Dekker,Inc,1979

[15]Sole A De,Kac V G.On Integral Representations Of q-Gamma And q-Beta Functions.Rend Mat Lincei,2005,9:11–29

[16]Tuan V K.New Type Paley Wiener Theorems for the Modified Multidimensional Mellin Transform.J Fourier Analysis and Appl,1998,4(3),12 pages

[17]Wang M K,Li Y M,Chu Y M.Inequalities and in finite product formula for Ramanujan generalized modular equation function.Ramanujan J,DOI 10.1007/s11139-017-9888-3:1–12

[18]Wang M K,Chu Y M.Refinements of transformation inequalities for zero-balanced hypergeometric functions.Acta Mathematica Scientia,2017,37B(3):607–622

[19]Yang Z H,Zhang W,Chu Y M.Shapr Gautschi inequality for parameter 0＜p＜1 with applications.Math Inequal Appl,2017,20(4):1107–1120

[20]Yang Z H,Qian W M,Chu Y M,Zhang W.On rational bounds for the gamma function.J Inequal Appl,2017,2017:Article 210,17 pages

[21]Yang Z H,Chu Y M.Asymptotic formulas for gamma function with applications.Appl Math Comput,2015,270:665–680

[22]Zhao T H,Chu Y M,Wang H.Logarithmically complete monotonicity properties relating to the gamma function.Abstr Appl Anal,2011,2011:Article ID 896483,13 pages

[23]Zhao T H,Chu Y M.A class of logarithmically completely monotonic functions associated with a gamma function.J Inequal Appl,2010,2010:Article 392431,11 pages

[24]Zhang X M,Chu Y M.A double inequality for gamma function.J Inequal Appl,2009,2009:Article ID 503782,7 pages

[25]Zhao T H,Chu Y M,Jiang Y P.Monotonic and logarithmically convex properties of a function invloving gamma function.J Inequal Appl,2009,2009:Article ID 728612,13 pages