谈谈类比推理
2018-05-05河南省许昌市建安大道许昌高级中学胡银伟
■河南省许昌市建安大道许昌高级中学 胡银伟
类比是人们从已经掌握了的事物的属性,推测正在研究中的事物的特性,它以原有认识作基础,类比出新的结果,由于类比的结果往往是带有猜测性的,故其结果不一定可靠,但它却是提出新问题和做出新发现的重要源泉,具有发现的功能。
进行类比推理时,应从具体问题出发,通过观察、分析、联想进行对比,提出猜想,找到合适的类比对象是解题的关键。类比推理常见有以下三种类型的应用。
类型一 类比定义
由已知熟悉定义类比新定义。
例1 定义“黄金椭圆”:如图1所示,椭圆中心在坐标原点,F为左焦点,当时,其离心率为,此类椭圆被称为“黄金椭圆”。类比“黄金椭圆”,试推算出“黄金双曲线”的离心率e等于( )。
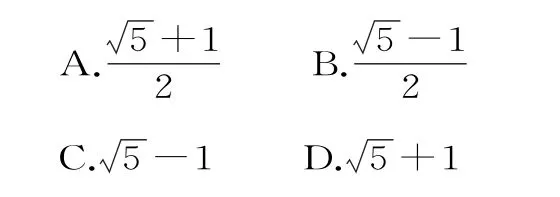
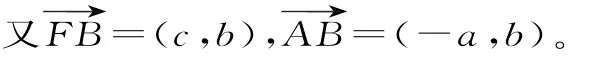
故b2=ac。而b2=c2-a2,所以c2-a2=ac。
在等号两边同除以a2得
故答案为A。
方法总结:在求解类比定义型推理试题时,可以借助原定义来求解。
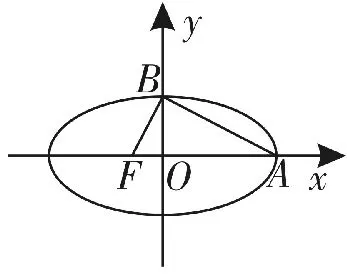
图1
跟踪训练1:定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫作等和数列,这个常数叫作该数列的公和。
已知数列{an}是等和数列,且a1=2,公和为5,那么a18的值为____,这个数列的前n项和Sn的计算公式为____。
解析:由等和数列的定义,知a1+a2=a2+a3=a3+a4=…,即有a1=a3=a5=…,a2=a4=a6=…。又a1=2,公和为5,得a18=a2=5-2=3,即有
类型二 类比性质
性质类比的常见情形有:平面与空间的类比;低维与高维的类比;等差数列与等比数列的类比等。
例2 在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则推广到空间可以得到类似结论。已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则等于( )。

解析:如图2,正三角形的内切圆与外接圆为同心圆,其半径分别为r1,r2,且r1∶r2=1∶2,所以类比此性质知正四面体P-ABC的内切球与外接球为同心球,其球半径分别为r、R,则
如图3所示,正四面体P-ABC中,过点P作PE⊥平面ABC,则E为底面正三角形ABC的中心,球心在PE上,设为O,于是OA=OP=R,OE=r,设正四面体棱长为a,则中有
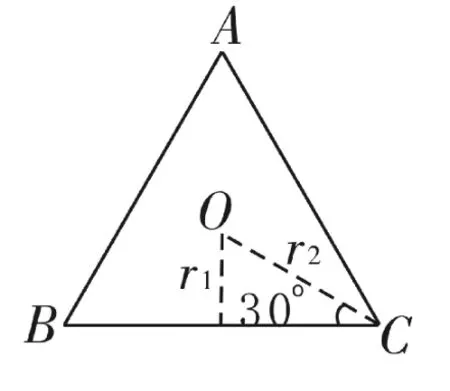
图2
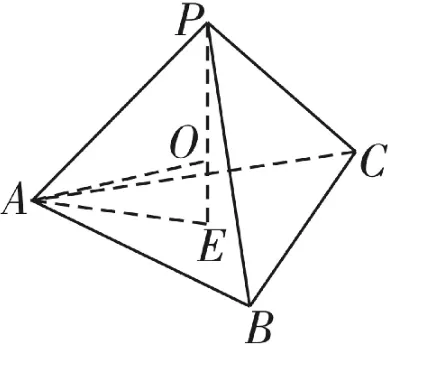
图3
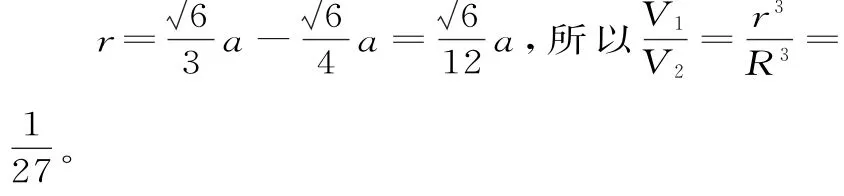
故答案为D。
方法总结:从一个特殊式子的性质、一个特殊图形的性质入手,提出类比推理型问题,求解时要认真分析两者之间的联系与区别,深入思考两者的转化过程是求解的关键。
类型三 类比方法
方法类比是由已知熟悉的处理方法类比未知问题的处理方法。常见问题有:数的运算(和与积,乘与乘方,差与除,除与开方)与向量运算类比,圆锥曲线间的类比等。
例3 给出下面类比推理(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”类比推出“a,c∈C,则a-c=0⇒a=c”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“a,b,c,d∈Q,则
④“若x∈R,则|x|<1⇒-1<x<1”类比推出“若z∈C,则|z|<1⇒-1<z<1”。
其中类比结论正确的个数为( )
A.1 B.2 C.3 D.4
解析:类比结论正确的有①②。
故答案为B。
方法总结:有一些处理问题的方法具有类比性,可以把这种方法类比应用到其他问题的求解中。同学们要注意知识的迁移。
跟踪训练2:已知△ABC的顶点A、B分别是离心率为e的圆锥曲线的焦点,顶点C在该曲线上。一同学已正确地推得:当m>n>0时有e(sinA+sinB)=sinC。类似地,当m>0,n<0时,有____。

故答案为e|sinA-sinB|=sinC。
此外,我们在进行类比推理时要尽量从本质上去类比,不要被表面现象迷惑,否则只抓住一点表面现象的相似甚至假象去类比,就会犯机械类比的错误。
