基于深度学习的城市地面公交客流集散点刷卡客流预测——以常州市为例

徐 特, 陈学武, 杨 敏, 吴静娴

(东南大学 交通学院， 南京 210096)

公交客流预测研究由来已久，但是针对地面公交客流集散点的刷卡客流预测问题依然值得继续探究. 从ITS设备获取的交通数据比传统方法获取的交通数据拥有更加大的量级和准确性，这使得研究人员可以更加深入地研究交通运输工程领域的相关内容，如交通流量预测、交通需求预测、出行时间预测与公交停站时间预测等. Yussof S等[1]开发了一种季节差分自回归移动平均模型(Seasonal ARIMA)去预测短时交通流量；费祥[2]等提出了一种基于动态贝叶斯的线性模型(DLM)去预测高速公路实时的短期旅行时间，他们使用的数据是高速公路线圈数据；丁剑等[3]提出了一种基于差分自回归移动平均模型与支持向量机模型(ARIMA-SVM Model)结合的组合模型去预测快速公交车辆在站台的停靠时间，这个模型可以充分捕获停靠时间的线性与非线性特征. 同时，随着人工智能、机器学习技术的蓬勃发展和广泛应用，交通领域也受到了新兴技术的冲击，一些研究人员已经意识到将深度学习方法运用在交通运输工程研究领域中会带来很多益处. Toque等[4]使用长短期记忆递归神经网络对动态公交OD矩阵进行预测，并提出未来研究中应当考虑诸如天气和交通事故等外生变量的影响；Polson 等[5]利用深度学习方法预测芝加哥短时交通流量并考虑了极端天气的影响，提高了预测结果的精度；许海涛等应用深度学习中一种叫做堆叠式自动编码器预测短时BRT客流，模型考虑了天气、工作日和周末3个因素，并把它们作为哑元变量输入模型中. 本文在已有相关研究基础上，综合考虑天气、空间特征如土地利用特征等因素对模型结果的可能影响，提出了一种特征层融合的长短期记忆递归神经网络(Feature-fusion LSTM RNN)模型，用于预测城市地面公交集散点的智慧卡刷卡客流量.

1 方法概述

1.1 深层神经网络和递归神经网络

深层神经网络(DNN: Deep Neural Network)和递归神经网络(RNN：Recurrent Neural Network)是在交通预测领域广泛应用的深度学习算法. 在共享了反向传播(Back Propagation)神经网络的所有优点情况下，DNN已经克服了BP神经网络因为隐层数量局限性而导致的模型收敛性问题[6]. 在实际应用中，合理增加隐层数量有利于模型的拟合. 由于一般的深层神经网络无法理解数据在时间轴上的变化，因此模型不能捕捉数据在时间序列上的特征. 针对这些缺点，RNN模型被提出，RNN已经在高性能的语言识别技术、自然语言处理算法中得到广泛可靠的应用. 与前馈(Feed Forward)神经网络不同, RNN可以使用其内部储存器来处理任意输入序列. 图1是RNN隐层的内部结构，输入是以T为时间步长的向量序列x=(x1,x2,…,xT)，输出是一个隐藏的向量序列h=(h1,h2,…,hT).

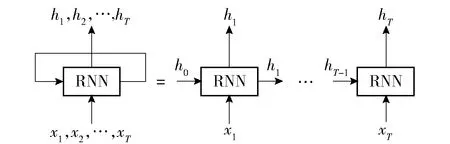
图1 RNN隐层的内部结构

在时间戳t处的隐藏单位值ht储存了包括前面时间步长的隐藏值(h1,h2,…,ht-1)和输入值(x1,x2,…,xt-1). 连同t中的输入，即xt，它在每次迭代中被传递到下一个时间戳xt+1. 通过这种方式，RNN可以记住多个先前时间戳的信息.

1.2 长短期记忆递归神经网络与特征层融合的长短期记忆递归神经网络

虽然RNN拥有很强的捕捉时间特征的能力，但他不能储存长期记忆信息. LSTM(Long Short-Term Memory)，作为一种特殊的RNN结构，可以克服记忆长期信息的缺点. 1个LSTM层由1个输入层、1个或数个隐藏层和1个输出层组成. 图2显示了单个LSTM层的内部结构.it,ft,ot-1,ct,(t=1,2,…,T)分别表示输入门、遗忘门、输出门和记忆单位向量，它们和ht共享相同的维度.

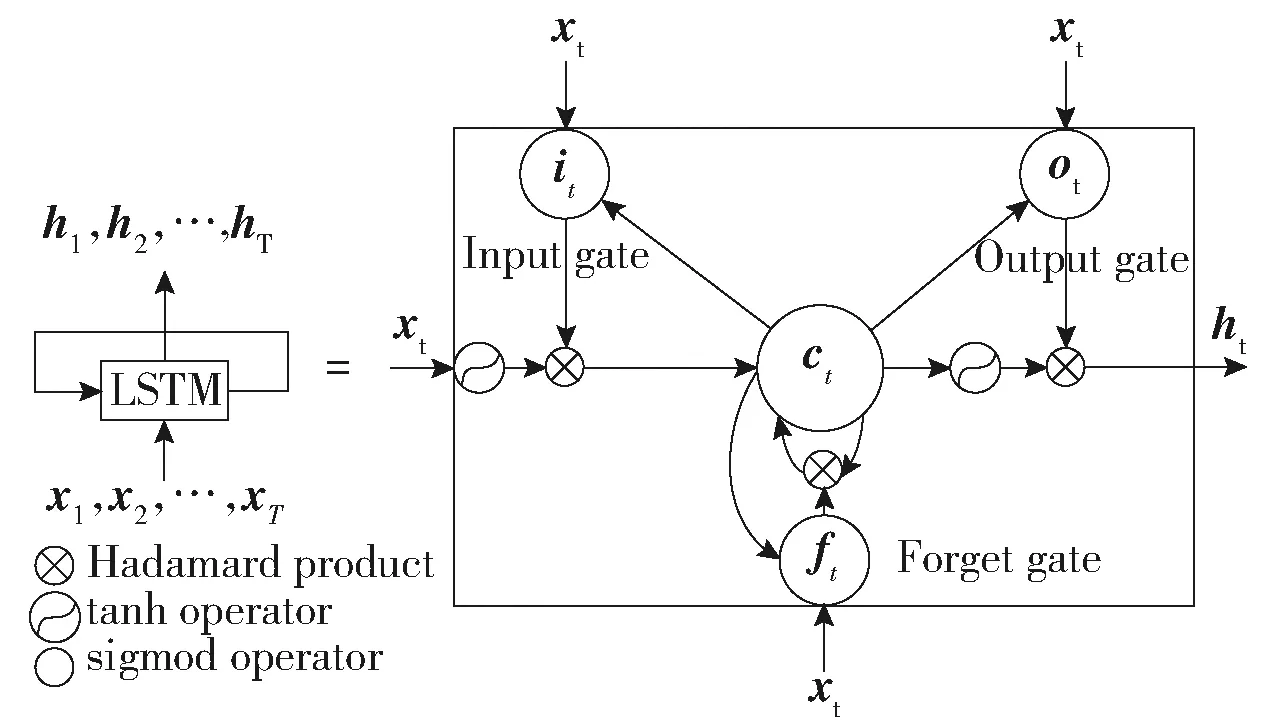
图2 单个LSTM层的内部结构

符号‘○’表示哈达马乘积(Hadamard product).σand tanh是2个非线性方程：

σ(x)=1/(1+e-x)

(6)

tanhx=(ex-e-x)/(1+e-x)

(7)

Wxi、Whi、Wci、Wxf、Whf、Wcf、Wxc、Whc、Wxo、Who、Wco是权重参数矩阵；bi、bf、bc、bo是截距参数. LSTM的记忆单元堆叠时，模型可发掘出输入和输出更深层次的关系. 图3是堆叠LSTM的结构示意图.

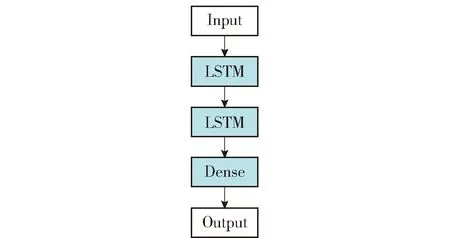
图3 堆叠LSTM结构示意图

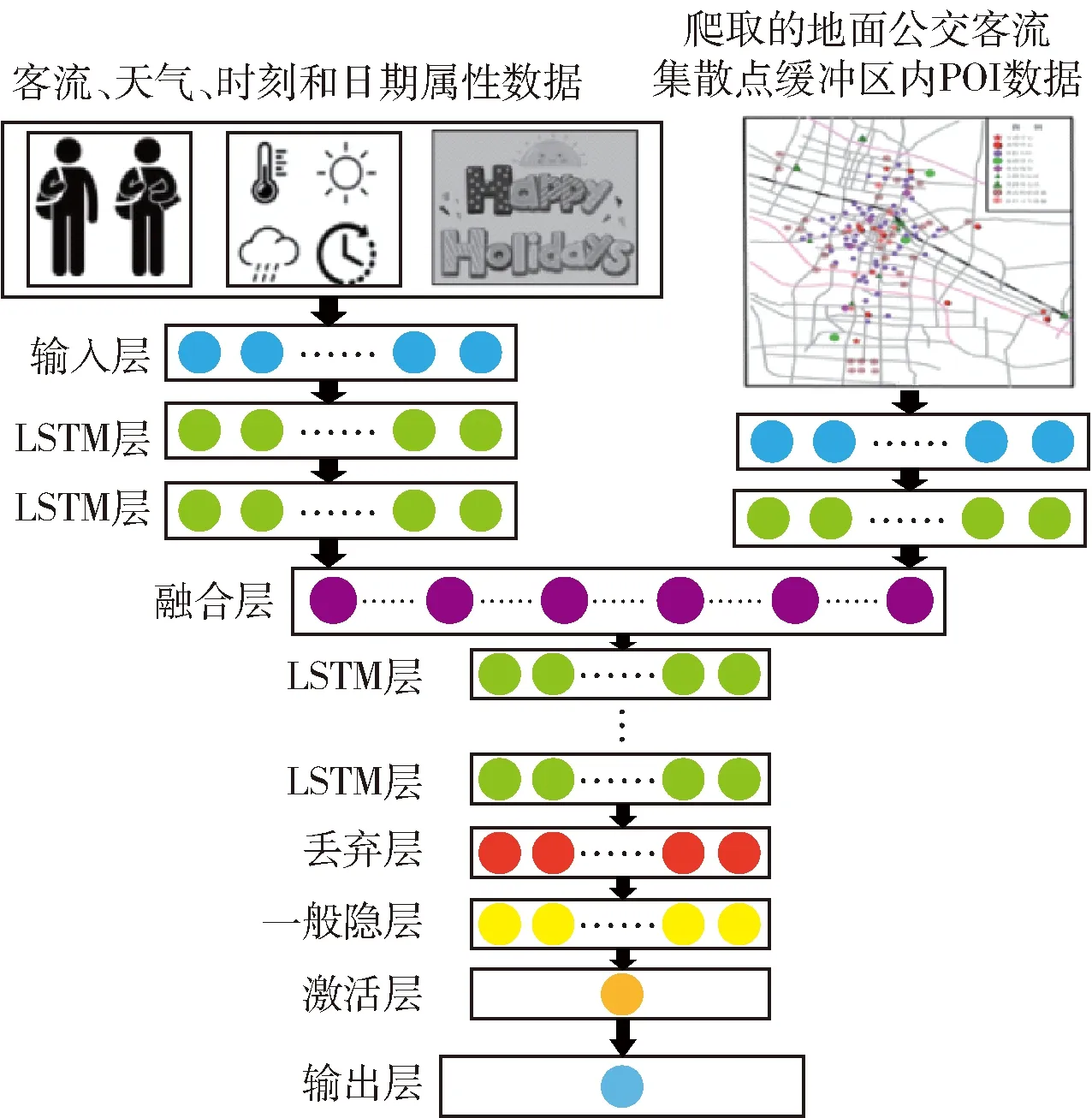
图4 特征层融合的长短期记忆递归神经网络示意图

2 数据概述

2.1 数据采集

从公交公司数据库中获取了2017年3月至6月的3 000多万条常州市的智慧卡刷卡数据. 与其他城市不同的是，常州市的智能卡记录包含了每次刷卡上车公交站台的全面信息，这省去了刷卡上车时间匹配的环节，大大提高了数据的准确性与可靠性. 同时我们也得到了常州市公交公司每条线路、每个公交站台的信息，这有助于精细化把控每个站点的具体情况.

然而，上述数据远远不够用于分析与建模. 在多数前人的研究中表明，天气和空间数据对城市客流带来显著影响[7]. 直观上来说，天气良好的时候，一些非通勤客流会显著上升，人们趋向于在好天气的时候外出游玩等. 同时，站点位于城市中心还是非中心，公共交通的客流量也会有较大的区别. 为了得到常州相关的天气数据，访问中国气象数据网是一个不错的选择.

同时，在地面公交客流集散点附近获取详细的土地利用信息或者建成环境信息是十分困难的，例如国土局等单位提供的图纸无法给出具体的、量化的职住信息、就业岗位数量信息等. 然而，随着百度地图API的开放，基于Python的爬虫可以获取相关数据. POI爬虫数据中文叫做兴趣点数据，可以在较大程度上反映土地利用的状况[8].

2.2 数据描述

1) 智慧卡刷卡数据 表1描述了从智能卡数据中获取的记录信息基本概况.

2) 公交站点信息 表2列出了常州市公交公司每条线路、每个公交站台的信息.

3) 天气数据 为从中国气象数据网上得到的天气数据，由于气象站数据是每隔3 h记录1次数据，稍后必须对数据进行插值处理.

4) POI爬虫数据 表4展示了基于百度地图API爬取的以地面公交客流集散点位中心半径的300 m缓冲区内的POI数据信息.

在相同宏观经办服务制度安排前提下，各统筹地区根据当地的特点探索并形成不同的经办模式。基于上述理论分析和实践经验，可以分析出不同模式都具有共同的构成要素，只是各要素在不同模式上体现不同。见表1

2.3 数据处理

2.3.1 融合多源数据

得到上述数据后需要进行多源数据融合，先是根据给定日期匹配智慧卡数据和天气数据集. 然后，将智慧卡每个时间戳的刷卡记录与相应的公交站点匹配. 最后，根据爬取的POI数据改善数据集质量. 以上所述数据集合并得到完整数据集然后计算每个站点每小时的客流量. 这是因为天气数据的粒度，我们决定预测每小时客流量. 研究所选取13个客流集散点位置，这些点位有的在常州市中心，有点位于郊区，这样选择有利于分析不同用地对客流预测结果的影响，时间段为3月15日至6月14日每小时的刷卡客流量. 所有步骤在Microsoft SQL server 2015中完成.

表2 常州市公交站点数据信息

表3 天气数据

表4 POI爬虫数据

2.3.2 分割数据集

得到完整数据集后，需要将数据集分为3个部分. 将3月15日至6月14日间70%的数据为训练集，20%的数据作为测试集用于评估检验模型，剩下10%的数据为交叉验证集，以防止过早停止训练[9].

3 数据分析

数据实验以预测下一个小时地面公交客流集散点的刷卡客流量来验证所提出方法的准确性. 实验与评价过程是在Python上编程基于Keras框架实现的，它具有直观的API接口可调用Google深度学习平台Tensorflow，并支持自动求导和更新速度快等优点.

所有数据实验过程都是在实验室台式机上进行(CPU：英特尔酷睿i7- 7700 3.40 GHz，32 GB内存，GPU：NVIDIA GTX 1080)，训练过程依靠NIVIDA公司生产的GPU完成，具有比CPU训练更快的速度.

3.1 数据实验设置

ARIMA模型不能很好地捕获客流的时空特征信息. 本文使用提出3种深度学习模型来预测刷卡客流量，包括：深度神经网络、堆叠的长短期记忆递归神经网络和特征层融合的长短期记忆递归神经网络模型. 对于上述深度学习模型，时间窗设置为6，这意味着模型是通过前6 h的刷卡客流去预测下一个小时客流. 在这之前需要注意的是一些不同尺度下的变量需要做哑元变换，是周几，是一个月中的几号又或者是否为节假日(是：1，否：0). 模型基于Adam优化器进行训练[9]. 为了防止模型过拟合，我们还在模型中加入了随机失活层[10].

3.2 结果评价方法

在对模型结果的评估中使用了平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分误差(MAPE)3个指标，计算公式如式(8)～(10)：

MAE=1N∑ni=0|xi-i|

(8)

RMSE=1N∑ni=1(|xi-i|)2

(9)

MAPE=1N∑ni=0|xi-i|i×100%

(10)

式中，xi为客流集散点的刷卡客流；i模型预测的结果. 平均绝对误差、均方根误差和平均绝对百分误差旨在测量预测值与实际值之间的误差.

3.3 数据拟合与结果

图5展示了模型拟合的过程，从图中可以看出，特征层融合的长短期记忆递归神经网络模型需要大约9 000多次迭代可以达到拟合. 图5和表5展示了地面公交客流集散点刷卡客流预测的结果. 在图6(a～d)中，实际值曲线是实际刷卡客流量，预测值曲线是模型预测的刷卡客流量. 长短期记忆递归神经网络-1训练时不包含POI数据，而长短期记忆递归神经网络-2包含了POI数据. 实验结果表明2个长短期记忆神经网络模型的效果要好于传统深度神经网络. 这一点可以证明反映土地利用信息的POI数据在一定程度上可以提高模型的精度. 观察MAE、RMSE和MAPE值，特征层融合的长短期记忆神经网络保持较低的值，这意味着在以上4个模型中，特征层融合的长短期记忆神经网络效果最好.

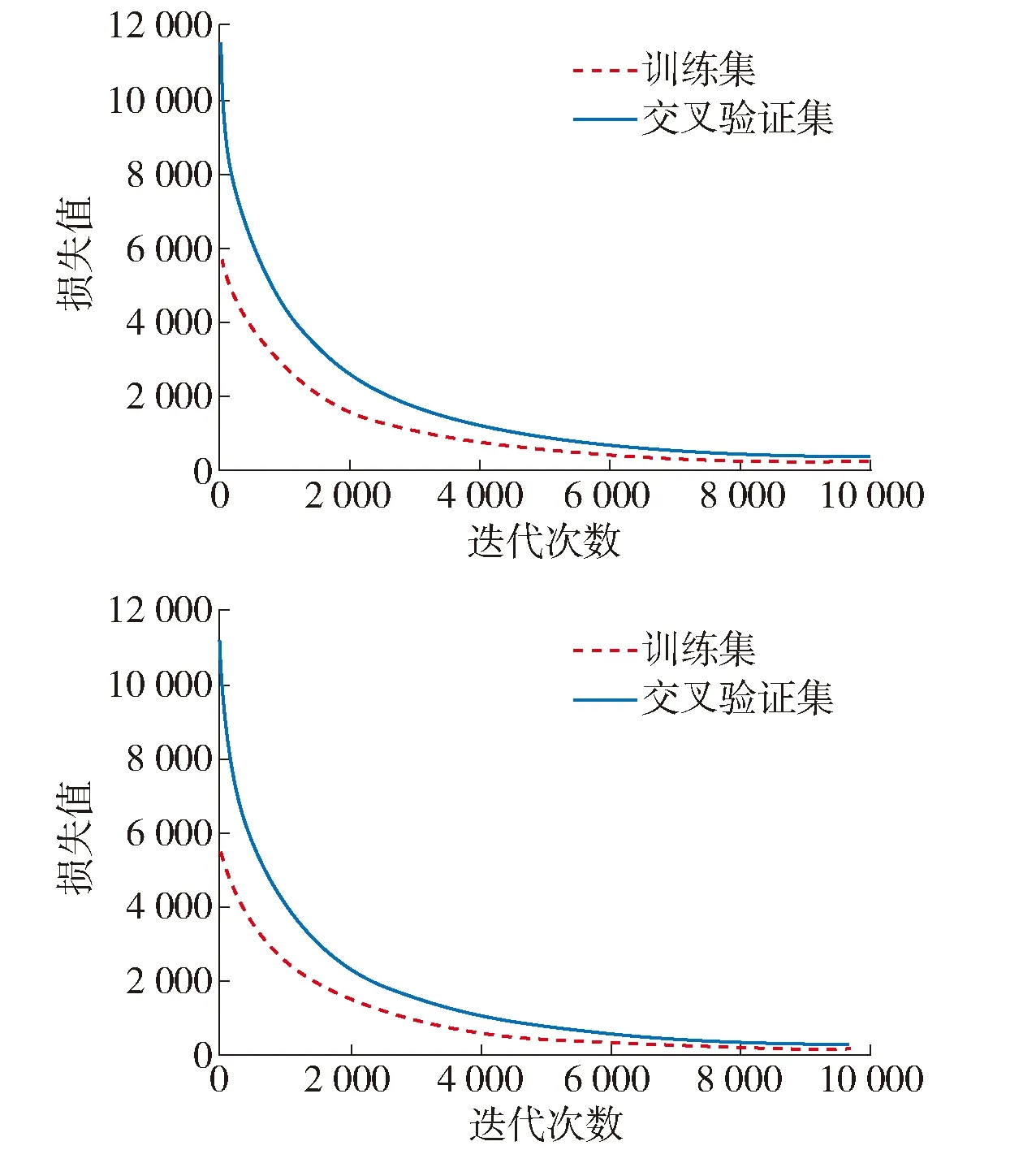
图5 特征层融合的长短期记忆递归神经网络模型拟合过程

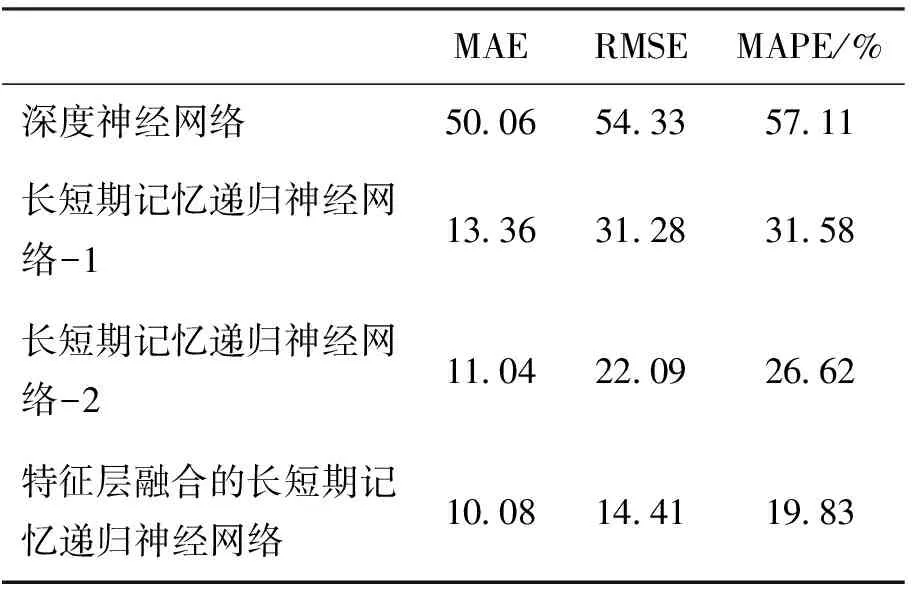
MAERMSEMAPE/%深度神经网络500654335711长短期记忆递归神经网络-1133631283158长短期记忆递归神经网络-2110422092662特征层融合的长短期记忆递归神经网络100814411983

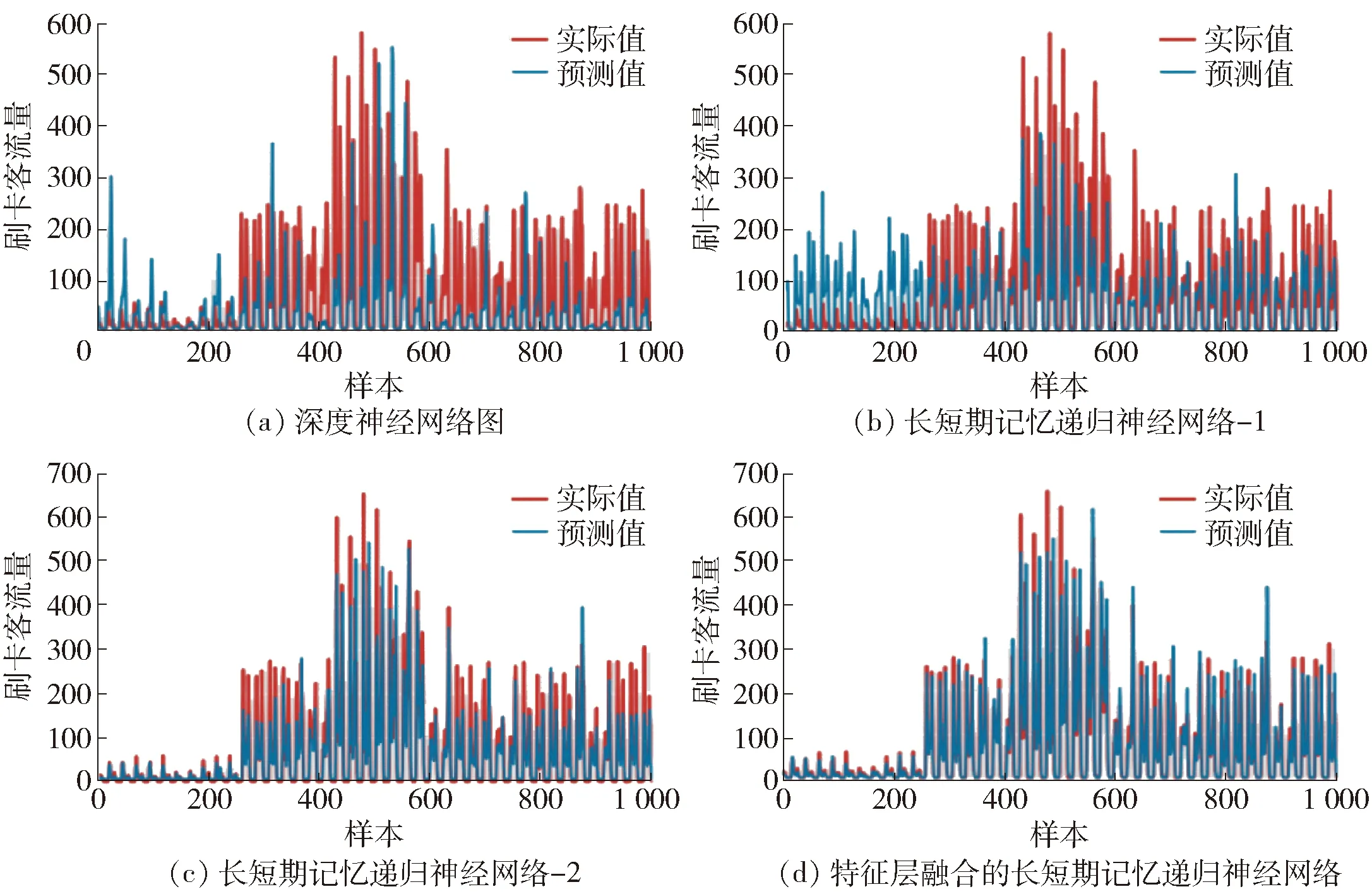
图6

4 结束语

本文提出了一种特征层融合的长短期记忆神经网络去预测城市地面公交客流集散点的刷卡客流，该方法与以往研究中使用的深度神经网络、长短期记忆递归神经网络相比，综合考虑了影响客流的时间因素与空间因素，如天气、土地利用信息等，取得了更好的准确性和泛化能力. 在未来的研究中，我们将考虑把更多的影响因素输入模型中，并提高模型的实时性，使用更短的时间间隔.

参考文献：

[1] Yussof S, Razali R A, See O H. An investigation of using parallel genetic algorithm for solving the shortest path routing problem [J]. Journal of Computer Science, 2011, 7(2): 206-215.

[2] Fei X, Lu C C, Liu K. A bayesian dynamic linear model approach for real-time short-term freeway travel time prediction [J]. Transportation Research Part C: Emerging Technologies, 2011, 19(6): 1306-1318.

[3] Ding J, Yang M, Cao Y, et al. Dwell time prediction of bus rapid transit using Arima-svm hybrid model [J]. InApplied Mechanics and Materials, 2014, 587: 1993-1997.

[5] Polson N G, Sokolov V O. Deep learning for short-term traffic flow prediction[J]. Transportation Research Part C: Emerging Technologies, 2017, 79: 1-17.

[6] Cheng Q, Liu Y, Wei W, et al. Analysis and forecasting of the day-to-day travel demand variations for large-scale transportation networks: Adeep learning approach. DOI: 10. 13140/RG. 2. 2. 12753. 53604.

[7] Zhang J, Zheng Y, Qi D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In AAAI (pp. 1655-1661).

[8] Wang J, Yang Y L, Zhou B, et al. The OD matrix estimation model of passenger flow based on the POI around the bus station[J]. International Journal of Applied Decision Sciences, 2017, 10(2): 118-130.

[9] King D P, Ba J. Adam: A method for stochastic optimization[J]. the 3rd International Conference for Learning Representations, 2014 arXiv preprint arXiv: 1412. 6980.

[10] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting [J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958.