装配式预应力混凝土分体箱梁模型修正及参数分析

2018-05-04贾圣东戴江波高庚元

土木工程与管理学报 2018年2期

蒋亮, 贾圣东, 李永, 戴江波, 高庚元

(1. 贵州省高速公路开发集团有限公司, 贵州贵阳 550004; 2. 中铁大桥局集团有限公司，湖北武汉 430050)

在城市环线高架快速路中，装配式预应力混凝土分体箱梁凭借其较大的截面抗扭强度和抗弯强度、合理的弯曲应力分布、较小的剪应力、良好的稳定性、造价低、施工速度便捷等特点，应用极为广泛。

钟新谷[1]根据预应力混凝土连续箱梁桥的特点，将裂缝按照形成原因分为9种，并且基于连续介质力学理论，推导了考虑翘曲、横向弯曲引起的二次应力的预应力变截面混凝土箱梁的空间分析的U.L.列式；王培金[2]对某一级公路的两片装配式预应力混凝土小箱梁进行了单梁静载试验，通过与Midas Civil理论计算模型的对比，发现理论值低估了结构的刚度并且会带来结构的安全性冗余；王素娟等[3]对一根长约30 m的预应力混凝土小箱梁进行了静力加载试验，对跨中底面和侧面的混凝土应变及部分底部钢筋应变进行了测量，通过布置连续应变片找出初始开裂过程，结果发现，在设计承载力作用下，试验梁远未达到破坏，裂缝最大宽度为0.20 mm，卸载后裂缝基本闭合；严国兵等[4]针对某高速公路预制小箱梁跨中腹板出现的斜向裂缝，通过荷载试验结合非线性有限元计算对其进行了受力性能评估和病害成因分析，认为防撞墙能够较好地参与梁体受力，在结构设计时，对于防撞墙施工顺序与构造设置应予以明确的指导。

预应力小箱梁在标准跨径和梁高上已经取得了较高的统一度，但在顶板厚度、腹板厚度、底板厚度等参数上的确定仍存在较多分歧[5]，进而导致过低的模板反复使用。因此，针对预应力混凝土分体箱梁的力学性能和参数指标进行研究，判断其能否满足设计要求，对于结构的安全性具有重大意义。本文基于“尖小”项目段设计施工方案采取的预应力小箱梁进行足尺静力载荷试验，对预应力小箱梁进行了模型修正及参数分析，并且为今后的优化设计亦能够提供一定的参考依据。

1 装配式预应力混凝土分体箱梁静力试验

1.1 试验目的

针对预应力小箱梁，对其抗弯承载能力进行评定，判断其能否满足设计要求，并且进一步探索预应力小箱梁在多种载荷工况下的结构受力状态。

预应力参数：管道摩阻系数0.17，管道偏差系数0.0015，一端锚具变形及钢束回缩量0.006 m，钢束张拉控制应力1395 MPa，钢束松弛率3%。

1.2 试验方案

静力试验主要针对预应力小箱梁在检测荷载作用下，其关键截面(测试截面)的混凝土应变，尤其是腹板应变、上下缘应变，钢筋应变，梁底挠度，以及箱梁裂缝等变化情况，从而探讨预应力小箱梁的力学特性。

1.2.1测试截面及测点布置

测试截面分为支座中心处截面、变截面、1/4截面、跨中截面及相应的对称截面，共计7个截面，如图1a所示。图1b所示为挠度测点布置截面。图1c～1g为各个截面的应变测点布置。

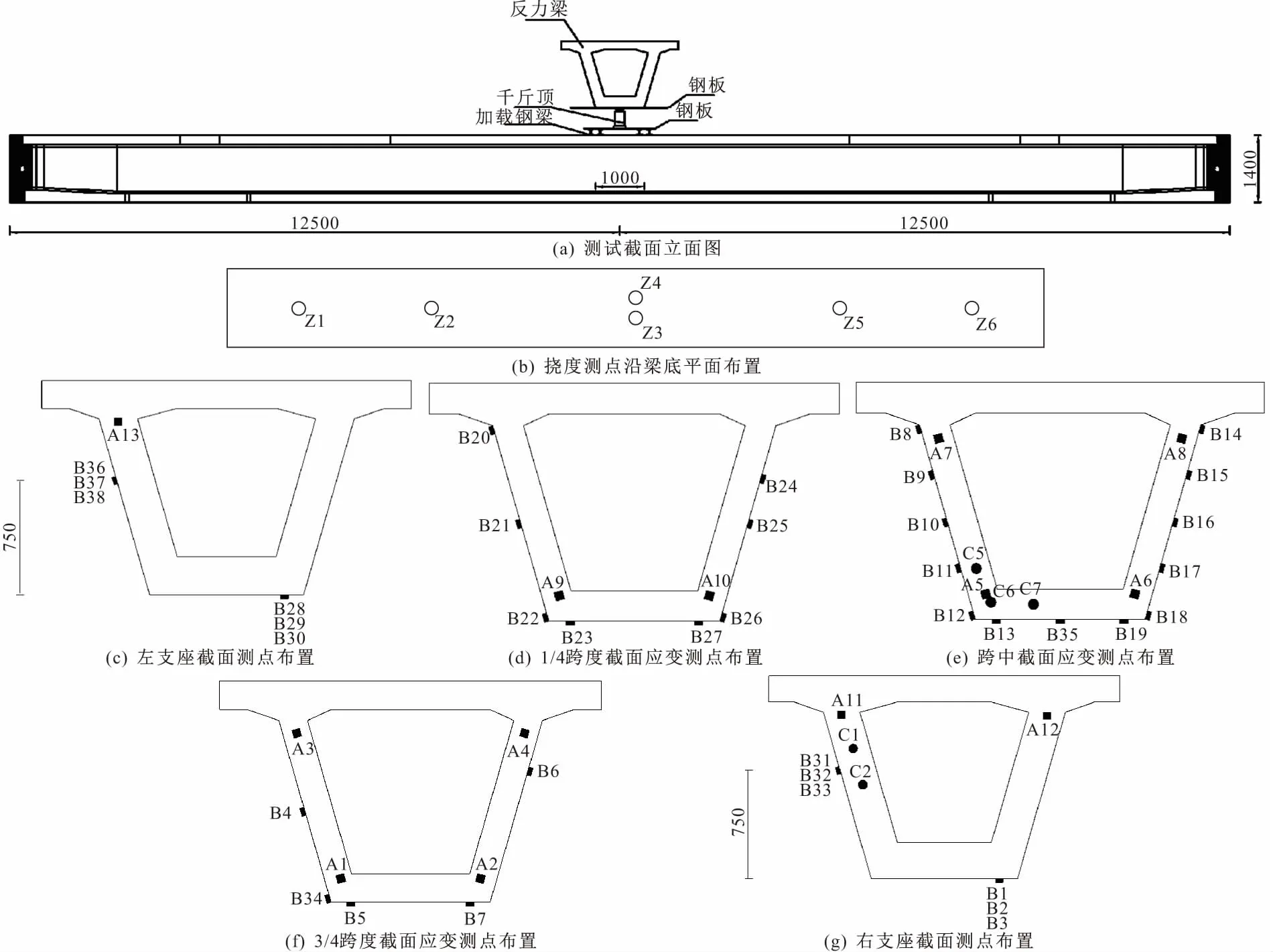
图1 测试截面与测点布置/mm注：(1)图中Z表示位移计，A表示混凝土应变计，B表示混凝土外表面应变片，C表示钢筋应变计；(2)图中B1, B2, B3、B28, B29, B30, B31, B32, B33和B36, B37, B38均表示一组应变花

1.2.2试验荷载确定

本次试验采用设计标准荷载作为试验荷载。首先利用Midas/Civil 建立单梁模型，根据文献[1]中的刚性横梁法得出横向分布系数为0.511(已根据车道数进行折减)，并以跨中截面作为试验控制截面，通过结构分析程序计算设计标准荷载作用下的试验梁成桥阶段跨中弯矩，然后按照内力等效原则反算出裸梁控制弯矩，作为试验控制荷载。根据计算，本次加载采用跨中弯矩1920 kN·m的弯矩值进行控制。

1.2.3加载方式

本试验加载采用集中加载方式，考虑到现场施工环境的限制，利用梁厂闲置小箱梁进行布载。试验加载采用1个液压千斤顶和油泵进行，加载速度控制在3 kN/s。

试验荷载分六级加载：0%，20%，40%，60%，80%，90%，100%；卸载分四级：70%，50%，30%，0%。分级加载控制如表1所示。

1.3 试验结果

受篇幅影响，图2仅显示静载试验部分数据结果，试验加载至100%时，梁底最大拉应变为132 με，跨中截面腹板中部B9#，B10#，B11#测点应变极值分别为-37 με，40 με，80με。而1/4截面腹板中部B21#，B24#，B25#测点应变极值分别为50 με，50με，80με。整个试验过程中，箱底最大挠度为7.62 mm，平均挠度为7.47 mm，小于规范规定的容许挠度(计算跨径的1/600)；加载过程中预应力混凝土边箱梁的荷载-挠度曲线近乎呈线性，表明混凝土处于弹性状态。试验过程中，所测预应力混凝土边箱梁、中箱梁均未见裂缝。

表1 分级加载控制

图2 试验结果

2 装配式预应力混凝土分体箱梁有限元模型

2.1 初始状态下有限元模型

利用大型有限元通用软件ANSYS建立装配式预应力混凝土分体箱梁单片梁有限元模型，构件单元类型及材料属性如表2所示，混凝土用solid65单元模拟，预应力钢筋用link8单元模拟，通过对其进行耦合处理模拟混凝土单元与预应力钢筋之间的作用，对link8单元采取降温法模拟预应力的效果，支座处设置弹性垫块，以减缓应力集中问题。有限元模型如图3所示。

计算结果如图4所示。图4a显示初始状态下装配式预应力混凝土分体箱梁(中跨中梁)竖向最大位移为 +4.909 mm，上拱程度并不明显，与试验实测数据9.8 mm有较大偏差，原因可能是由于混凝土收缩徐变等综合因素引起的梁拱度增长。

表2 构件单元类型及材料属性

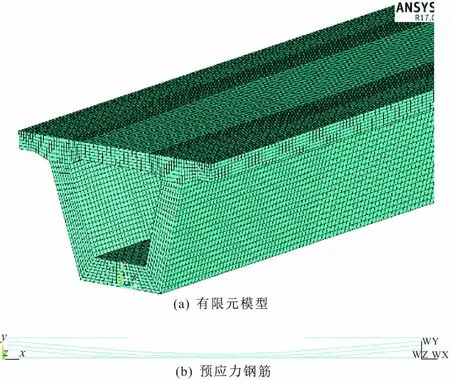
图3 有限元模型

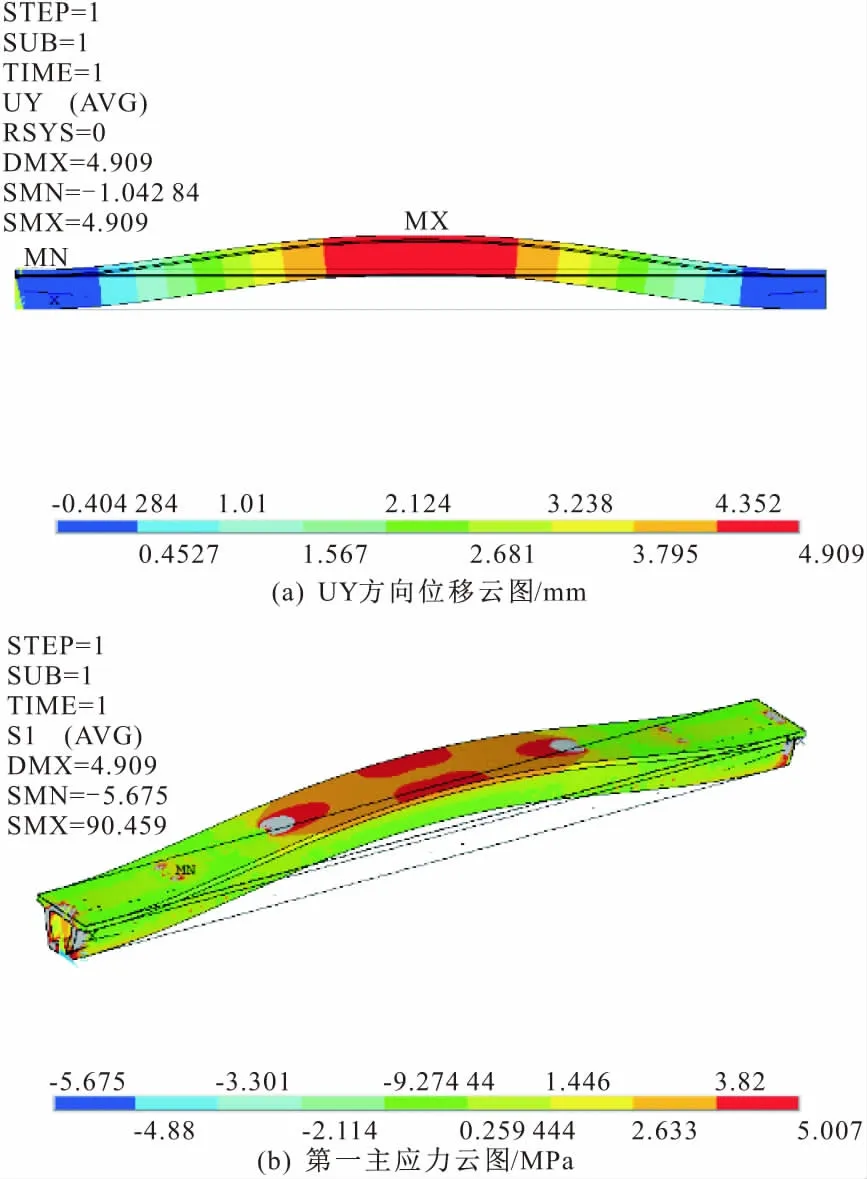
图4 初始状态结构响应

有限元模型中混凝土单元第一主应力的跨度在-5.675 ～5.007 Mpa范围内，而C50混凝土单轴抗拉强度仅为1.83 Mpa，此为应力集中的表征现象。图4b显示，小箱梁端部混凝土与预应力筋锚固区域、跨中上拱混凝土与负弯矩钢束端部连接处出现了大于2 MPa的情况，小箱梁整体模型里绝大部分混凝土单元第一主应力大小仍然保持在1.446 Mpa以内。

2.2 加载状态下有限元模型

如图5所示跨中下挠为3.304 mm，混凝土单元第一主应力区间为-1.000～2.359 Mpa，绝大部分混凝土单元集中在-0.254～1.239 Mpa之间，比较符合实际情况。在小箱梁支座上端及1/4梁长处，腹板节点第一主应力变化较为明显突出，相应的底板处更是存在大于混凝土单轴抗拉强度的部分。支座处上端箱梁顶板混凝土单元存在应力集中问题，局部为1.613 Mpa。

图5 加载状态结构响应

3 装配式预应力混凝土分体箱梁静力学模型修正

3.1 修正理论

以有关试验实测值与计算值的差值为目标函数，引入一定的约束条件，对结构的一些参数进行优化，使优化以后的参数能够反映结构的真实状态。本文选用的方法为静力位移残差矩阵方法，基于挠度的残差值建立目标函数，有限元模型力与位移之间关系如式(1)[2]所示。

K·U=F

(1)

式中：K为结构总刚度矩阵；F为荷载向量；U为结构位移向量。

静力试验中测得的有限点的位移，将位移值分为已测量位移值Ua和未测量位移值Ub，则有：

(2)

结构的位移残差矩阵eu为：

eu=[Kaa-Kab·(Kbb)-1·Kba]-1·

[(Fa)m+Kab·(Kbb)-1·(Fb)m]-(Ua)m

(3)

式中：m表示实测值。通过调整修正参数使结构静力位移残差取得最小值。

静力试验中，结构的位移测试精度较高、稳定性好，且一定程度上可以反应结构整体效应[3]，因而本文采取位移模式，并以式(4)作为目标函数[4]f(X)为：

(4)

3.2 静力学模型修正结果

通过ANSYS的一阶优化算法，目标函数收敛容差为0.001，迭代步数为50次。模型计算值与修正值比较如表3所示，表4显示了部分单元参数初始值与修正值，最终，目标函数从0.0863降到4.381×10-4。

表3 模型计算值与修正值 mm

表4部分单元参数初始值与修正值

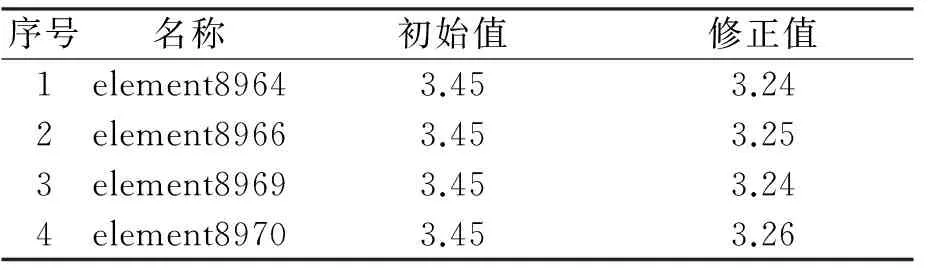
×104 MPa

4 装配式预应力混凝土分体箱梁模型参数分析及参数指标抗裂性评价

选取箱梁的若干几何参数和材料参数，作为参数指标对抗裂性作出评价[5]。

4.1 参数选择和功能函数确定

4.1.1参数选取

(1)几何参数

几何参数选择箱梁底板厚度hy1a(端部截面)及hy2a(跨中截面)、箱梁顶板厚度hy1d(端部截面)及hy2d(跨中截面)、箱梁腹板厚度t1(端部截面)及t2(跨中截面)、箱梁梁高h、箱梁底板宽度b1和箱梁顶板宽度b2。

(2) 材料参数

材料参数选择混凝土重度densc、预应力钢筋重度denspres、混凝土弹性模量emcon和预应力钢筋弹性模量emprest。

为了得到几何参数(hy1a，hy2a，hy1d，hy2d，t1，t2，h，b1，b2)及材料参数(densc，denspres，emcon，emprest)对装配式预应力混凝土分体箱梁的力学性能影响规律，本文选取了81个模型来进行计算和比对。

4.1.2功能函数确定

基于正截面抗裂的力学性能评价标准，根据 JTG D62-2004 公路钢筋混凝土及预应力混凝土桥涵设计规范，预应力混凝土受弯构件应按下列规定进行正截面抗裂验算，全预应力混凝土构件在作用(荷载)短期效应组合下预制构件满足：

σst-0.85σpc≤0

(5)

式中：σst为在荷载短期效应组合下构件抗裂验算边缘混凝土的法向拉应力；σpc为扣除全部预应力损失后的预加力在构件抗裂验算边缘产生的混凝土预压应力。

4.2 结果分析

图6a所示为各个几何参数偏移对目标函数的影响。可以看出，除了梁高以外，其他几何参数曲线均呈现向下的趋势，换言之，底板厚度、顶板厚度、腹板厚度、底板宽度和顶板宽度等几何参数，随着其偏移量的增加，目标函数减小，而随着梁高的偏移量增大，目标函数增加。其中，腹板厚度的偏移量关于目标函数的斜率最大，即表示腹板厚度对于装配式预应力混凝土分体箱梁正截面抗裂的影响最为明显，底板厚度与顶板厚度次之，底板宽度与顶板宽度的影响较弱。

图6b所示为各个材料参数偏移对功能函数的影响。由图可见，所有材料参数曲线均呈现向下的趋势，换言之，混凝土重度、预应力钢筋重度、混凝土弹性模量和预应力钢筋弹性模量等材料参数，随着其偏移量的增加，功能函数减小。其中，混凝土弹性模量和预应力钢筋弹性模量的偏移量关于功能函数的斜率较大，即表示混凝土和预应力钢筋的弹性模量对于装配式预应力混凝土分体箱梁正截面抗裂的影响较为明显，而混凝土重度与预应力钢筋重度对于装配式预应力混凝土分体箱梁正截面抗裂的影响相对较小，尤其是预应力钢筋重度，几乎对于抗裂没有影响。