直面相异构想，调正转化路径——以“平行四边形面积计算公式的推导”教学为例

□ 杨文杰

在几何图形的学习过程中，学生原有的经验能对几何学习产生促进作用，但是也有可能产生一些负面影响。学生在解决新的问题时，可能会受到一些无关特征的影响，从而导致认知错误或者误解，从而产生对新事物的错误认知，也就是对新知识的错误的相异构想。在“平行四边形的面积”一课教学中，很多学生产生平行四边形的面积就是邻边相乘这样的错误的相异构想。而我们在教学中，要基于这样的错误构想，进行教学实践，从而达到从“错误”到“正确”的调正目的。

一、相异构想产生的原因分析

学生产生平行四边形面积计算方法就是邻边相乘这样错误的相异构想，是受到以往知识概念、学习经验、心理因素等多种因素的影响。

几何视觉的错误判断：我们知道长方形是特殊的平行四边形，两组对边分别平行且相等。在观察两个性质类似，大小、边长等差距比较小的图形时，学生的几何视觉就直接认同了两个图形面积计算的相似性，有些学生则会直观认为面积大小相等。“很像”和“真实”是不同的，这部分学生仅仅凭借几何视觉就定义了平行四边形面积计算方法，从而导致产生错误的相异构想。

上位知识学习程度影响：平行四边形面积的上位知识是面积的概念。欧几里得几何概念的建构认为：学生学习面积概念是基于测量能力的发展，同时指出学生习得面积概念的发展形成于十五岁左右。受到个体心理发展差异的影响，五年级的有些儿童，测量能力还停留在长度和距离一维程度，无法建立二维层面上的测量。而在学习平行四边形面积前，学生学习了长方形面积，所以简单地把平行四边形面积计算方法思考为“长×宽”。

图形运动观念的缺乏：平行四边形面积的计算公式推导过程是基于转化的思想，而这个转化其本质是图形的剪拼，也就是图形的变换与运动。图形的变换概念的形成也是源自学生的生活经验，针对这一内容的学习，学生不仅要具有图形的直觉，而且要具有图形会动的直觉。产生“S＝ab”的错误相异构想，并不是学生头脑中无转化思想，而是恰巧有了转化的想法，却存在着转化过程中的错误。这个错误形成的原因主要是学生在转化过程中缺乏图形变换的经验，缺少对于图形整体拼组过程中整体的运动的面积守恒的认识。

几何推理能力的不足：学生错误地把平行四边形面积计算为邻边相乘，是学生几何推理能力不足的体现。因为没有一定的操作指导（学生对模型、图形或表象进行思维操作），所以学生只能“直觉”对“空想”，这对于平行四边形面积计算的推导是没有根据的，所以产生错误的相异构想也是情有可原的。这一阶段儿童的几何推理能力还不能脱离直观的操作实验，这也是我们教师在课堂上需要补足的短板。

综上分析，在平行四边形面积的学习过程中，学生错误的相异构想形成是基于学生在解决新问题中已经有了初步的“转化”意识，但缺乏严谨的“转化”方式（面积守恒），从而导致错误的转化结果（S=ab）。

二、相异构想调正转化的路径

基于学生的错误相异构想，我们需要给学生提供诊断的调正路径，引发学生的认知冲突，从而有效地根除学生的错误概念。当然借鉴别人的教学经验，选择最优的调正路径，也不失为一种好的策略方法。以下笔者将从本节课的引入—调正—反馈来实现平行四边形面积计算公式从“异”到“正”的调正目标。

调正引入：不规则图形面积比较，引入“转化”思想

师：同学们，我们已经学过面积，下面两个图形哪个图形的面积大，你是怎么想的？（出示

生：一样大。因为都有12格。

师：你是通过数格子的方法来比较的是吗？

生：是的。

师：一个图形包含有几个单位面积，面积就是多少。

师：还有不同的方法进行比较的吗？

生：我是把图形①中的那个凸出来的部分移到下面，正好变成了和图形②一模一样的长方形。所以它们的面积相等。

生：形状变了，面积没变。周长变了。（生上台手指）

师：是的，像这样经过分割、移补后图形的面积没有改变，这也是数学中所说的“出入相补”原理。

【设计意图】学生的原有认知已经有了转化的意识，只是在转化的过程中缺乏面积守恒的概念。为了弱化其他因素，特别是为了摒弃长方形面积公式的干扰，笔者借鉴苏教版和北师大版教材的编排，用不规则图形面积大小比较来引入学习。呈现格子图的目的是为了让学生的认知回归到事物的原点，即面积的本质属性——单位面积的累加。分割、移补图形的过程让学生直面面积转化“形变而积不变原理”，形成面积守恒的概念。

调正初阶：借助格子图，回归面积本质的探索纠正

师：同学们，我们也学过平行四边形了，这个平行四边形的面积是多少？（出示你是怎么想的？

生1：数格子，36平方厘米。

师：你是怎么数的？

生1：满格是1平方厘米，超过半格的也是1平方厘米，不足半格的就忽略。

师：你是用估计数的方法，还有其他数的方法吗？

生2：我数出来是35平方厘米，我发现左边的那个不足1平方厘米的格子可以拼到右边，正好是1格。

生：每行有7个，这样的有5排，5×7＝35（平方厘米）。

师：你还有其他的想法吗？

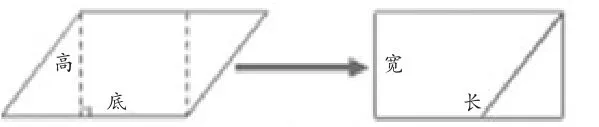
生3：我也是像陈科航（生2）一样的方法，只是我不是一格一格补的，我是一大块移的（上台移动，见右图）。

生：长方形。

师：转化的过程中，你发现什么变了，什么没变。

生：面积没变，高也没变；形状变了，那一块平移过来了。

师：现在你能知道原来平行四边形的面积吗？

生：35平方厘米，也就是算长方形的面积。

师：还有其他不一样的想法吗？

生4：我还可以对半剪开，再拼成一个长方形，面积也能算出来。

师：这一个方法和刚才的方法有什么相同的地方，有什么不同的地方？

生：都是转化成了长方形。

生：面积都一样。

生：也可以用算式7×5来快速算出面积。

生：不一样，剪的大小不一样。

师：剪的大小不一样，怎么剪的？

生：都是竖着剪的，但剪的地方不一样，所以比刚才的三角形大了很多。

师：竖着剪，那是沿着什么剪的？

生：哦，都是沿着高剪的。

师：我们刚才在格子图的帮助下成功地计算出了平行四边形的面积。这一学习过程，你有什么心得想和大家分享吗？

生：我们可以沿着高，把平行四边形转化成长方形来计算面积。

【设计意图】图形的运动想象是比较复杂的，特别是二维图形的组合。而格子图其实就是单位面积，借助格子图进行操作实验，是一把很好的辅助梯。学生可以借助格子图产生多种剪拼方法，例如生2的想法，就是单位面积的累加，是一种回归面积本质的想法；例如生4的想法，是大板块的拼组，在这个过程中，学生必须分离出更抽象的格子结构进行拼组，说明学生的思维经过前面的辅助已经开始慢慢脱离了背景的限制。这一环节的调正过程，学生已经明白了平行四边形的面积与斜边无关。

调正进阶：从特殊到一般，发展几何推理能力

操作探究1：刚才，我们借助格子图来计算平行四边形的面积。现在老师给每个小组一些平行四边形，你们去想办法求出它们的面积。（学具：底边7cm，高3cm，斜边5cm；底边10cm，高3cm，斜边5cm）

生小组合作探究，教师巡视。

汇报：（通过剪拼成长方形）第一个面积是21平方厘米，第二个面积是30平方厘米。

师：计算了三个平行四边形的面积，你觉得平行四边形的面积和什么有关？

生：与高有关，与底有关，与长方形有关。

师：与长方形有什么关系？

生：求平行四边形的面积，其实是转化成长方形的面积，长方形的宽就是平行四边形的高，长方形的长就是平行四边形的底。

师：与斜边无关。

操作探究2：提供一个标有字母的平行四边形，利用字母进行面积公式推导。

师：如果用S表示平行四边形的面积，用a表示平行四边形的底，用h表示平行四边形的高，平行四边形面积的计算公式你会表示吗？

生：S等于a乘h。根据学生回答板书：

长方形面积=长×宽

平行四边形面积=底×高

【设计意图】学生的几何推理能力发展需要经历想象、思考、操作、计算等过程。这一调正过程中学材的选择从具象到抽象，从特殊到一般，最后到用字母进行公式推理。在对比中强化辩证，理清平行四边形的面积=底×高，与斜边无关。这一过程不仅是学生相异构想的调正过程，更是几何推理能力锻炼与发展的过程。

调正反馈：寻找反例，从变化的角度看问题

练习活动1：下面的平行四边形面积相等吗？

练习活动2：活动平行四边形的拉升过程，你有什么发现？

反馈：什么没变？平行四边形的面积怎么变化？为什么？

【设计意图】学生相异构想调正后，设计反馈的练习，可以是正强化，也可以是反例强化。练习活动1是再次在变与不变中感受等底等高的平行四边形的面积相等，平行四边形的面积与斜边无关，同时面积相等的平行四边形的形状可能不同。练习活动2的设计目的是为了让学生在反例中明白，底边和斜边相等的平行四边形的面积不一定相等，原因是高不相等；同时渗透极限思想——随着高的变小，面积越来越小，最终趋向于0。

学生相异构想的形成是基于其知识结构、思维能力和活动经验的。通过分析其相异构想形成的原因，针对形成原因进行调正路径的学习和分析，借鉴前人的活动经验，设计有针对性的引入环节，可操作性的调正活动，有探究性的调正过程，有正反两方强化的反馈练习，能帮助学生纠正错误的想法，提高学生的推理能力，丰富数学的活动经验。

参考资料：

[1]杨灵君、陈庆宪.回归认知本真关注自主经历——“平行四边形的面积”教学实录与评析[J].小学教学(数学版),2013(12):22-24.

[2]李帮魁.简单之中见丰厚——特级教师姜锡春执教“平行四边形的面积”教学赏析[J].教育科学论坛，2013（10）：46-47.

[3]沈燕.基于学生，为了学生——贲友林老师“平行四边形的面积计算”教学赏析[J].小学教学（数学版），2015（6）:70-73.

[4]潘小明.数学思维的发展不是空洞的——“平行四边形的面积”教学实践及思考[J].人民教育（教学），2012（12）：34-37.